Теоретическая часть

1. Производная и дифференциал

Пусть функция f определена в V(x₀). Придадим точке х₀ произвольное приращение так, чтобыx₀+xV(x₀). Тогда функция f(x) получит приращение _.

Определение 1. Производной функции f в точке х₀ называется предел при отношения приращения функции к вызвавшему его приращению аргумента, если этот предел существует.

Обозначается ,,,,.

Таким образом, по определению 1 .

Пусть f имеет производную в каждой точкеx множества D. Поставим в соответствие точке хD производную функции в этой точке: . Это соответствие определяет функциюаргументах, определённую на D. Она называется производной функцией от функции f.

Определение 2. Функция f(x) называется дифференцируемой в точке х₀, если её приращение в этой точке, соответствующее приращению аргумента, может быть представлено в виде

,

где - некоторое число, не зависящее от,

- функция от , бесконечно малая при, т.е..

Теорема 1 (необходимое и достаточное условие дифференцируемости). Для того, чтобы функция f(x) была дифференцируема в точке х₀ необходимо и достаточно_, чтобы она в этой точке имела производную , при этом.

Т. о., приращение дифференцируемой в точке х₀ функции f(x) имеет вид

.

Из теоремы 1 получаем второе определение дифференцируемой в точке функции.

Определение 3. Функция f(x) называется дифференцируемой в точке х₀, если она в этой точке имеет конечную производную.

Операция нахождения производной функции f(x) в точке или на множестве называется дифференцированием функции f(x).

Теорема 2 (непрерывность дифференцируемой функции). Если функция f(x) дифференцируема в точке х₀, то она непрерывна в этой точке.

Определение 3. Пусть функция f(x) дифференцируема в точке х₀. Дифференциалом функции f(x) в точке х₀ называется главная часть приращения функции, линейно зависящая от приращения аргумента .

Обозначается dy, . Т. о., согласно определению

.

Рассмотрим функцию ,, то есть для независимого аргументах дифференциал и приращение совпадают: .

Определение 4. Дифференциалом независимой переменной х называется ее приращение :.

Тогда из определения дифференциала следует

.

2. Уравнения касательной и нормали

Геометрический смысл производной состоит в следующем: производная функции f(x) в точке х₀ равна угловому коэффициенту касательной к кривой y=f(x) в точке (х₀;f(x₀)) (равна тангенсу угла наклона касательной к положительному направлению оси Ох)

Т. о., если функция f дифференцируема в точке х₀, то график этой функции имеет касательную, угловой коэффициент которой равен .

Тогда уравнение касательной имеет вид

.

Прямая, проходящая через точку M₀(x₀;y₀) и перпендикулярная к касательной, называется нормалью к графику функции f в точке M₀(x₀;y₀). Тогда 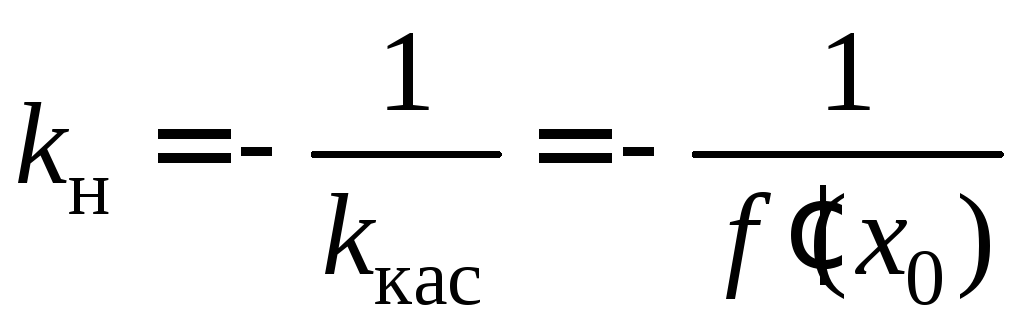, и, значит, уравнение нормали имеет вид

.

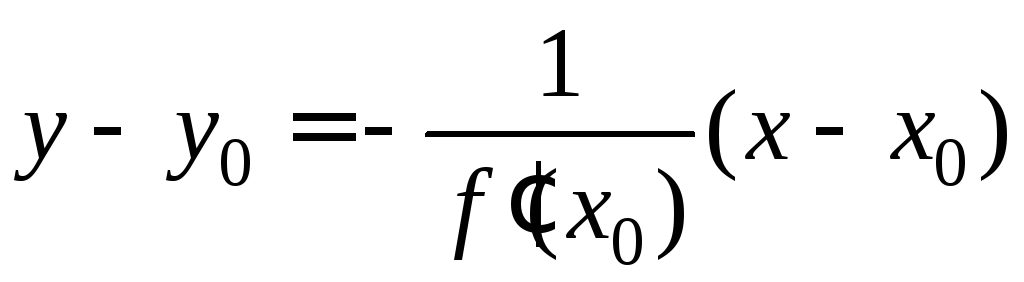3. Правила дифференцирования

Теорема 3. Если функции u=u(x) и v=v(x) дифференцируемы в точке х, то в этой точке дифференцируемы их сумма, произведение и (при условии, что ) частное, при этом справедливы равенства

,

,

.

Следствие 1. Если u(x) дифференцируема в точке х, а , то функцияy=Cu(x) также дифференцируема в точке х и .

Следствие 2. Если функции u=u(x) и v=v(x) дифференцируемы в точке х, то в точке х дифференцируема их разность y=u(x)-v(x), причем

.

Теорема 4. Если функция t=(x) дифференцируема в точке х₀, а функция y=f(t) дифференцируема в точке , то сложная функцияy=f((x)) дифференцируема в точке х₀, и для производной в этой точке имеет место формула:

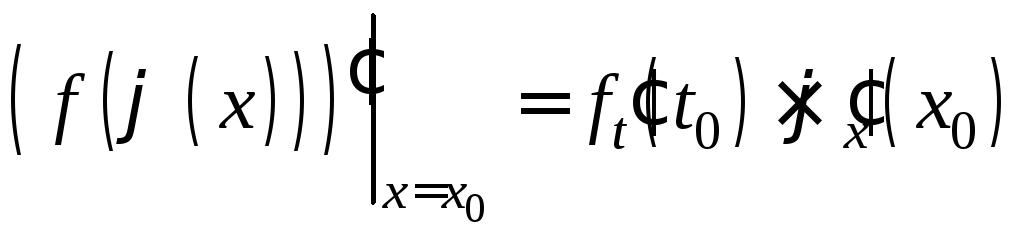
(кратко:).