
Интегральное исчисление
.pdf
и существует конечный или бесконечный предел
lim f (x) k.
x (x)
Тогда а) если интеграл
(x)dx
a
сходится и 0 k , то сходится и интеграл
f (x)dx;
a
б) если интеграл
(x)dx
a
расходится и 0 k , то интеграл
f (x)dx
a
тоже расходится.
В частности, если k = 1, то есть функции f(x) и (х) эквивалентны при x , то интегралы
|
|
f (x)dx u |
(x)dx |
a |
a |
сходятся и расходятся одновременно.
При применении признака сравнения удобно сравнивать подынтегральную функцию с функцией
x1 , 0,
для которой сходимость или расходимость соответствующего несобственного интеграла легко установить непосредственно. Пусть 1, тогда
При = 1
1
a x
|
1 |
|
|
|
|
b |
|
|
|
|
x |
1 |
|
b |
|||
|
|
|
|
|
|
|
|
|
|||||||||
|
dx lim |
x dx lim |
|
|
|
|
|||||||||||
|
|
1 |
|||||||||||||||
a |
x |
|
|
|
b |
a |
|
b |
|
|
a |
||||||
|
|
|
|
|
x1 b |
|
x1 a |
|
( 1) |
||||||||
lim |
|
|
|
|
|
|
|
. |
|||||||||
|
|
|
|
x1 a |
|
|
|||||||||||
|
|
|
|
||||||||||||||
|
b |
|
1 b |
|
1 a |
|
|
|
|
|
( 1) |
||||||
|
|
|
|
1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|||
|
b |
1 |
|
|
|
|
|
b |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
dx lim |
dx lim ln|x| |
|
lim(ln b ln a) . |
||||||||||||||
x |
|
||||||||||||||||
|
a |
|
|
|
|
|
a |
|
b |
|
|
||||||
b |
|
|
|
b |
|
|
|
|
|
|
|||||||
Следовательно,
91

|
|
|
1 |
|
|
|
|
|
|
|
|
dx |
|
|
|||
|
|
|
|
|
||||
|
|
a |
x |
|
|
|||
|
|
|
|
|
|
|
||
сходится при > 1 и расходится при < 1. |
|
|
||||||
Пример. |
|
|
|
|
|
|
||
Исследуем на сходимость |
|
|
|
|
|
|
||
|
2x 7 |
|
|
|||||
|
|
|
|
|||||
|
|
|
dx. |
|
|
|||
x3 |
x2 |
5x 12 |
|
|
||||
1 |
|
|
|
|
|
|
|
|
При x подынтегральная функция эквивалентна |
2 |
.. Таким образом, = |
||||||
x2 |
||||||||
|
|
|
|
|
|
|
||
2 > 1, и данный интеграл сходится.
Абсолютная сходимость несобственных интегралов 1-го рода
Несобственный интеграл
f (x)dx
a
называют абсолютно сходящимся, если сходится интеграл
| f (x)|dx.
a
Функция f(x) называется при этом абсолютно интегрируемой на [a, ).
Признак абсолютной сходимости несобственного интеграла (критерий Коши) – без доказательства.
Для того чтобы
f (x)dx
a
абсолютно сходился, необходимо и достаточно, чтобы для любого > 0 существовало такое , что при ’ > , ’’ >
| f (x)|dx .
Теорема 2. Если интеграл
f (x)dx
a
абсолютно сходится, то он сходится и в обычном смысле. Доказательство.
Согласно критерию Коши
92
|
|
|
|
|
|
|
f (x)dx f (x)dx |
|
f (x)dx |
|
| f (x)|dx |
. |
|
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, существует конечный предел
|
|
f (x)dx |
npu b, |
a |
|
то есть рассматриваемый интеграл сходится.
Несобственные интегралы от функций с бесконечными разрывами (несобственные интегралы 2-го рода)
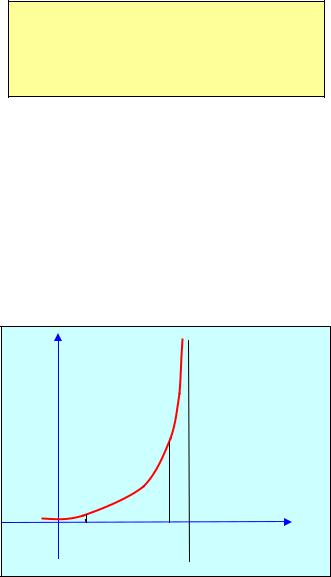
Пусть функция f(x) определена и непрерывна при a < x < b и имеет разрыв
b
при x = b. Тогда f (x)dx определяется следующим образом:
a
b b
f (x)dx lim f (x)dx (2) |
|
|
0 |
a |
a |
и называется несобственным интегралом 2-го рода. Если предел, стоящий справа, существует и конечен, интеграл называется сходящимся, в противном случае – расходящимся.
Аналогичным образом определяются несобственные интегралы от функции, имеющей разрыв при х = а:
b |
|
b |
|
f (x)dx lim |
|
f (x)dx, |
|
|
0 |
|
|
a |
a |
|
|
у |
|
|
|
|
y=f(x) |
|
|
|
|
|
|
а |
b |
х |
|
|
|
|
|
Рис. 2
и от функции, разрывной в точке с (a<c< b):
93
b |
с |
b |
f (x)dx f (x)dx f (x)dx,
a |
a |
с |
если существуют оба интеграла, стоящие в правой части равенства.
Для несобственных интегралов 2-го рода справедливы те же утверждения, что и для несобственных интегралов 1-го рода:
Теорема 3(признак сравнения). Пусть функции f(x) и (х) непрерывны при a x b и имеют разрыв при x = b. Пусть, кроме того,
0 (x) f (x) npu |
x [a,b). |
Тогда:
1)если интеграл
b
f (x)dx
a
сходится, то сходится и интеграл
b
(x)dx;
a
2) если интеграл
b
(x)dx
a
расходится, то расходится и интеграл
b
f (x)dx.
a
Теорема 4. Если f(x) – знакопеременная функция, непрерывная на [a,b) и имеющая разрыв при x =b, и если
b
| f (x)|dx
a
сходится, то сходится и интеграл
b
f (x)dx.
a
Замечание 1. Эти теоремы доказываются так же, как теоремы 1 и 2. Замечание 2. При выполнении условий теоремы 4 несобственный интеграл
b
f (x)dx
a
называется абсолютно сходящимся, а функция f(x) – абсолютно интегрируемой.
Следствие из теоремы 3. Если
94
|
|
|
|
f (x) |
|
|
1 |
|
npu x b, |
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
(b x) |
||||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
то при < 1 |
f (x)dx сходится, а при > 1 расходится. |
|||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
1 |
b |
|
|
|
|
|
b |
|||||
|
|
dx (b x) dx lim (b x) dx |
||||||||||||
|
|
|
||||||||||||
|
a |
(b x) |
a |
|
|
|
|
|
0 |
a |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b a)1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
, 1; |
||||
|
|
|
|
|
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
lim(ln(b |
a) ln ) , 1; |
||||||||||
|
|
|||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
lim |
|
, 1. |
||||||
|
|
|
|
|
1 |
|
(1 ) |
1 |
||||||
|
|
(1 )(b a) |
|
0 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, интеграл |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
b |
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
dx |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
a |
|
(b x) |
|
|
||||
сходится при < 1 и расходится при > 1.
Примеры решения задач
Задача 1.
Вычислить несобственный интеграл
|
x |
|
|
|
|
|
|
dx |
|
(x |
3) |
4 |
||
0 |
|
|
||
|
|
|
|
или установить его расходимость.
Указание
Вычислите определенный интеграл
B |
x |
|
|
|
|
|
|
dx |
|
(x |
3) |
4 |
||
0 |
|
|
||
|
|
|
|
и найдите его предел при B .
Решение
95
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
x |
|
|
|
dx lim |
|
|
|
x |
|
dx lim |
|
(x 3) |
3 |
dx |
|
|
|
|
|||||||||||||||||||||
|
|
|
(x 3) |
4 |
(x 3) |
4 |
4 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
B |
0 |
|
|
|
|
B |
0 |
|
(x 3) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
B |
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
B |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
(x |
|
|
3 |
(x 3) |
4 |
|
|
|
|
|
|
2 |
|
(x 3) |
3 |
||||||||||||||||||||||||||||||
|
|
B |
0 |
|
3) |
|
|
|
|
|
B |
|
|
|
2(x 3) |
|
|
|
|
0 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
||||||||
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||||||||||||||||
|
2(B |
|
2 |
18 |
(B |
3) |
3 |
|
|
27 |
|
18 |
27 |
54 |
|
|
||||||||||||||||||||||||||||||
|
|
|
B |
|
|
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
54 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 2.
Вычислить несобственный интеграл
|
1 |
|
|
|
dx |
||
x2 4x 13 |
|||
|
|
|
или установить его расходимость.
Указание
Представьте данный интеграл в виде суммы двух несобственных интегралов:
|
|
|
1 |
0 |
|
|
1 |
|
|
|
1 |
|
|
|
|
dx |
|
|
dx |
|
|
dx |
|||
x |
2 |
4x 13 |
x |
2 |
4x 13 |
x |
2 |
4x 13 |
||||
|
|
|
|
0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
и вычислите каждый из них по отдельности.
Решение
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx; |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x |
2 |
4x 13 |
|
x |
2 |
4x 13 |
|
|
x |
2 |
4x 13 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
4x 13 |
|
2 |
4x |
|
|
|
13 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
A A x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
d(x 2) |
1 lim arctg |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
A |
|
(x 2) 9 |
|
|
|
|
|
|
|
3 A |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
arctg |
A 2 |
|
|
|
1 |
arctg |
2 |
|
|
; |
|
|
|
|||||||||||||||||||
|
|
|
|
|
lim arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
3 A |
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
6 |
|
|
|
|
|||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 lim |
|
|
|
x 2 |
|
B |
|
|
|
|
1 arctg |
2 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dx |
arctg |
|
|
|
|
|
; |
|||||||||||||||||||||||||||||||||
x2 |
|
4x 13 |
|
|
|
|
3 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
B |
|
|
3 |
|
|
|
|
|
|
|
|
6 3 |
|
|
|
|
|
|
||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
dx |
|
|
3 arctg |
3 6 |
|
|
|
|
|
3 arctg |
|
|
|
3 . |
|
||||||||||||||||||||||||||||||||
|
|
x2 4x 13 |
|
|
|
6 |
|
3 |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
96

Ответ: 3 .
Задача 3.
Указать, при каких значениях k сходится интеграл
|
dx |
|
|
|
|
. |
|
k |
x |
||
e |
x ln |
|
|
|
|
|
Указание
Сделайте замену t = ln x и определите порядок малости подынтегральной функции относительно функции t1a , несобственный интеграл 1-го рода от которой сходится при a > 1 и расходится при a < 1.
Решение
|
dx |
|
|
1 |
|
|
t ln x |
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
d ln x |
|
|
|
|
dt |
|
x ln |
k |
x |
ln |
k |
x |
t |
k |
|||||||
e |
|
e |
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
сходится при k > 1.
Ответ: k > 1.
Задача 4.
Вычислить несобственный интеграл
1 |
|
1 |
|
|
|
|
|
dx |
|
1 |
x |
2 |
||
0 |
|
|
||
|
|
|
|
или установить его расходимость.
Указание
Подынтегральная функция имеет бесконечный разрыв при х = 1. Рассмотрите определенный интеграл
1 |
|
1 |
|
|
|
|
|
dx |
|
|
|
|
||
1 |
x |
2 |
||
0 |
|
|
||
|
|
|
|
и перейдите к пределу при 0.
Решение
|
1 |
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
dx |
lim |
|
|
|
|
|
|
dx |
|
lim |
|
|
|
|
|
|
|
|
|
dx |
|
|||||||||
|
1 x2 |
|
|
1 x2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
0 |
|
|
|
2 |
0 |
1 x |
|
1 |
x |
|
|
|
|||||||||||||||||||
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
|
|
1 |
|
|
|
ln |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 lim ln |
|
|
|
|
|
1 lim |
|
|
1 lim ln |
|
2 |
1 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
2 |
|
|
|
1 x |
|
|
0 |
|
2 |
0 |
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
97

интеграл расходится. Ответ: интеграл расходится.
Задача 5.
Вычислить несобственный интеграл
|
1 |
|
||
|
|
dx |
||
|
|
(x 1) |
||
x |
||||
0 |
|
|
|
|
или установить его расходимость.
Указание
Представьте данный интеграл в виде суммы двух интегралов:
|
1 |
|
1 |
|
1 |
|
|
1 |
|
|
|||||
|
|
|
dx |
|
|
dx |
|
|
dx, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
x(x |
1) |
0 |
|
x(x 1) |
1 |
|
x(x 1) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
первый из которых является несобственным интегралом 2-го рода от функции с бесконечным разрывом при х = 0, а второй – несобственным интегралом 1-го рода.
Решение
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
dx |
|
|
dx |
|
|
|
|
|
|
|
dx; |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
0 |
|
|
|
|
x(x |
1) |
|
|
|
|
0 |
|
|
x(x 1) |
|
1 |
|
|
x(x |
1) |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
t |
|
|
|
|
|
|
|
1 |
|
|
dt |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
dx lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
2 lim |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||
x(x |
1) |
|
|
|
x(x |
1) |
|
|
(t |
1) |
|
||||||||||||||||||||||||||||||||
0 |
|
|
|
0 2 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 lim arctg1 arctg |
|
; |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||||||||||||||||||
|
2 lim arctg t |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dx 2 lim arctg t |
|
|
|
2 |
|
|
|
|
|
|
|
; |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
x(x 1) |
|
|
|
|
|
B |
|
|
|
|
|
|
|
2 |
|
4 2 |
|
|
|
|||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x 1) |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: .
98
2.1.Дифференциальные уравнения 1-го порядка
2.1.1.Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка.
Изоклины. Задача Коши. Теорема существования и единственности задачи Коши
Уравнения, в которые неизвестная функция входит не только сама, но и под знаком производной или дифференциала, называются дифференциальными уравнениями. Подобными уравнениями описываются многие физические явления и процессы.
Примеры.
1) dxdt kx
уравнение радиоактивного распада (k – постоянная распада, х – количество
неразложившегося вещества в момент времени t, скорость распада |
dx |
|||||||
dt |
||||||||
|
|
|
|
|
|
|
||
пропорциональна количеству распадающегося вещества). |
|
|||||||
|
|
r |
ur r |
r |
|
|
|
|
2) |
m |
d2 r |
dr |
) |
|
|
||
dt2 |
F(t, r, |
dt |
|
|||||
|
|
|
|
|
|
|||
уравнение движения точки массы т под влиянием силы F, зависящей от
времени, положения точки, определяемого радиус-вектором r, и ее скорости r
drdt . Сила равна произведению массы на ускорение.
3) |
2u |
|
2u |
|
2u |
4 (x, y, z) |
|
|
x2 |
y2 |
z2 |
||||||
|
|
|
|
|
уравнение Пуассона, задающее зависимость между многими физическими величинами. Например, можно считать, что u(x,y,z) – потенциал электростатического поля, а (x,y,z) – плотность зарядов.
Мы будем рассматривать уравнения, где неизвестная функция является функцией одной переменной. Такие уравнения называются обыкновенными дифференциальными уравнениями.
Уравнение вида
|
|
(n) |
(x)) 0 (1) |
|
F(x,u(x),u (x),u (x),...,u |
|
|||
|
|
|
|
|
называется обыкновенным дифференциальным уравнением п-го порядка. При этом порядком уравнения называется максимальный порядок входящей в него производной.
Функция, которая при подстановке в уравнение (1) обращает его в тождество, называется решением дифференциального уравнения.
99
Дифференциальные уравнения первого порядка, разрешенные относительно производной
Рассмотрим уравнение вида
dydx f (x, y). (2)
Можно показать, что общее решение такого уравнения зависит от одной произвольной постоянной. С геометрической точки зрения уравнение (2) устанавливает зависимость между координатами точки на плоскости и
угловым коэффициентом dy касательной к графику решения в той же точке. dx
Следовательно, уравнение (2) определяет некоторое поле направлений, и задача его решения состоит в том, чтобы найти кривые, называемые интегральными кривыми, направление касательных к которым в каждой точке плоскости совпадает с направлением этого поля.
Примеры.
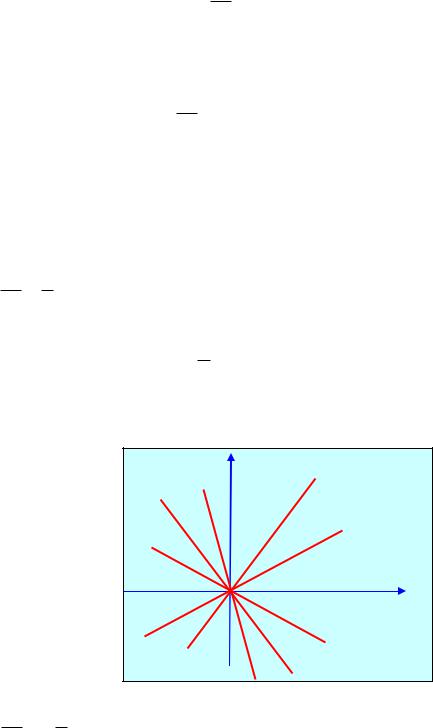
1)dydx yx .
Вкаждой точке, кроме начала координат, угловой коэффициент к искомой
интегральной кривой равен yx , то есть тангенсу угла, образованного с осью
Ох прямой, проходящей через данную точку и начало координат. Следовательно, интегральными кривыми в данном случае будут прямые вида
у = сх (рис.1).
у
х
Рис. 1
2)dydx yx .
Вэтом случае касательная в каждой точке плоскости перпендикулярна направлению прямой, проходящей через эту точку и начало координат, так
100
