RUDN-I

Переменные xm+1, . . . , xn перенесем в правую часть и получим:

Итак, в этом случае система имеет бесконечно много решений.

Замечание 4. В этом случае система (1) при любом столбце B правых частей разрешима и имеет бесконечно много решений. В частности, однородная система имеет не только нулевое решение.

e e

тождествами 0 = 0 и их можно отбросить. Далее, как в случае 3 (при

значения; а базисные переменные x1, . . . , xr выражаются через них по формулам

Вывод 2. При m = n имеетmatematemместо следующая альтернатива (альтер-

Замечание 5. Из приведенных выше ответов следует, что однородная система (1) в случаях 1 и 2 имеет единственное решение. Это нулевое решение x1 = x2 = . . . = xn = 0. В случаях 3 и 4 решений бесконечно много.

В заключение сформулируем некоторые выводы, важные для дальнейшего.

Вывод 1. Если число неизвестных в однородной системе (1) больше числа уравнений. т.е. n > m, то реализуются случаи 3 или 4 и, значит, заведомо существуют. ненулевые решения однородной системы.

натива Фредгольма):

1)либо однородная система имеет только нулевое решение, а соответствующая неоднородная система разрешима (причем единственным образом) при любом столбце правых частей B;

2)либо существуют ненулевые решения однородной системы, а соответ-

ствующая неоднородная система совместна не при любом столбце правых частей B.www

Действительно, при m = n может возникнуть либо случай 1, и тогда реализуется первая возможность (см. замечание 1), либо случай 4, и тогда реализуется вторая возможность.

Замечание 6. Отметим, что при m ≠ n альтернатива Фредгольма не имеет места (см. замечания 2 и 3).

При этомwwwсвободные переменные x3, x4 могут принимать любые значения. Каждому набору свободных переменных x3, x4 отвечает по формуле

(3) определенный набор базисных переменных x1, x2, т.е. определенное решение системы.

24 Тема 1. Системы линейных уравнений. Метод Гаусса

Замечание 7. Изложенный метод решения системы (1) допускает элементарные преобразования 2-го рода (перестановку столбцов матрицы A при приведении матрицы A к ступенчатому виду). Для практического решения систем это не вполне удобно, т.к. связано с перенумерацией неизвестных. Обычно, необходимость в перестановке столбцов матрицы A не возникает. Исключительная ситуация, которая может потребовать перестановки столбцов, возникает, если на некотором шаге k в

ми в k-ой строке), 1 ≤ j1 < j2 < . . . jr ≤ n (причем номера могут идти не подряд). Обратный ход метода Гаусса дает тогда простейшую матрицу,

в которой akjk = 1, k = 1, 2, . . . , r, а элементы над ними равны нулю. В этом случае переменные xj1 , xj2 , . . . , xjr являются базисными, а

остальные свободными. Перенося свободные переменные в правые части уравнений, получим систему, эквивалентную (1), в которой из r уравнений базисные переменные xj1 , xj2 , . . . , xjr однозначно выражаются через свободные, а остальные уравнения (если r ≤ m − 1) имеют вид

e

0 · xj1 + 0 · xj2 + . . . + 0 · xjr = bk, k = r + 1, . . . , m.

3) существованиеwww"нулевого элемента" , т.е. матрицы O, такой что A+O = O + A = A для любой матрицы A,

Если все bk = 0, то получим тождества 0 = 0. Их можно отбросить

1.4. Теоретические упражнения к теме 1

1.1. Показать, что сложение матриц обладает следующими свойствами:

1) коммутативность: A + B = B + A,

2) ассоциативность: A + (B + C) = (A + B) + C,

4) существование у каждой матрицы A ей противоположной −A, такой что A + (−A) = (−A) + A = O.

1.2. Показать, что умножение матрицы на число обладает следующими

1.4.Определим вычитание матриц: A − B := A + (−B). Показать, что 1) α(A − B) = αA − αB,

2) (α − β)A = αA − βA.

1.5.Показать, что транспонирование матрицы обладает следующими

свойствами:

1)(A + B)T = AT + BT ,

2)(αA)T = α · AT ,

3)(AT )T = A.

1.6.Матрица A называется эквивалентной матрице B, если она получена из нее с помощью конечного числа элементарных преобразований. Показать, что это отношение эквивалентности обладает свойствами:

1) рефлексивности A ≈ A,

2) симметричности A ≈ B B ≈ A,

3) транзитивности A ≈ B, B ≈ C A ≈ C.

1.7.1) Показать, что matematem

при условии,wwwчто числа x1, x2, x3 разные. Рассмотреть также случаи совпадения двух из них; совпадения всех трех чисел.

2) Показать, что для любых различных чисел x1, x2, x3 и любых чисел y1, y2, y3 существует, причем единственный многочлен p(x) степени не выше 2, такой что p(xi) = yi, i = 1, 2, 3. Каков геометрический смысл этого утверждения?

1.8. Доказать следующие утверждения о связи решений однородной и неоднородной системы линейных уравнений.

1) Сумма решений однородной и неоднородной системы является решением неоднородной системы.

26 Тема 1. Системы линейных уравнений. Метод Гаусса

2) Разность двух решений неоднородной системы является решением однородной системы.

28 Тема 2. Множества и отображения

Пустое множество, множество без элементов . Например,

{x R : 2 < x < 1} = .

Равенство множеств: A = B, если A B и B A, т.е. A и B состоят

Определение 2. Пересечение (произведение) C = A ∩ B определяется как множество элементов, принадлежащих и A, и B.

Определение 3. Разность C = A \ B определяется как множество элементов из A, не принадлежащих B.

Определение 4. Симметрическая разность задается равенством

Аналогично определяем сумму и пересечение любого (не обязательно конечного) семейства множеств:

Ясно, что C2 C1.

Пример 3. Показать, что A B = (A B) \ (B ∩ A).

(1)

Пусть x A B = (A \ B) (B \ A). Тогда x A \ B, либо x B \ A. Если x A \ B, то x A, x ̸B x A B, x ̸A ∩ B x

A B (A B) \ (B ∩ A).

2.2.Отношения эквивалентности. Фактор-множества

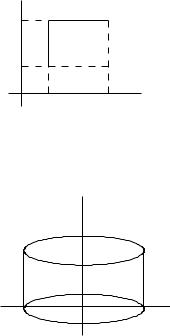
2) P = [a, b)×(c, d] = {(x1, x2) : a ≤ x < b, c < x ≤ d} — прямоугольник на плоскости.