
- •Введение
- •Дискретная математика
- •Бинарная операция ассоциативна, если тождественно выполняется: ;
- •4.Классы булевых функций :
- •X1 x2 X
- •5. Теория полноты
- •I этап :
- •3 Случай :
- •II этап :
- •1); 2); 3); 4).
- •1) ; 2); 3);
- •4) ; 5);
- •5.4. Полные системы в классах т0, т1, м, s, l.
- •5.5 Базисы в классах t0 , t1, s, m, l Все полные системы для классов t0, t1, s, m, l в утверждениях выше являются базисами для этих систем.
- •6 .Минимизация булевых функций
- •1 Этап:
- •2 Этап:
- •Достаточно ясна связь задачи нахождения тупиковых покрытий и минимизации функции покрытия.
- •7. Исчисления высказываний
- •8. Семь теорем
- •Доказательство полноты исчисления высказываний.
- •Представление графов
- •1. Задание графа с помощью матрицы смежности.
- •2. Задание графа с помощью матрицы инцидентности.
- •3. Задание графа с помощью списка смежности.
- •Связные графы
- •Алгоритмы нахождения компонент связности
- •1. Поиск в ширину
- •2. Поиск в глубину
- •Укладки графов
- •Теорема Эйлера
- •Критерий Понтрягина-Куратовского
- •Раскраски графов
- •Основные понятия комбинаторики.
- •1 1.2 Упорядоченные наборы элементов изn-данных
- •1.3 Неупорядоченные наборы элементов изданных без повторений.
- •1.4 Неупорядоченные наборы элементов изп данных с возможными повторениями.
- •2 Метод включения-исключения.
- •Упражнения.
- •3 Метод производящих функций
- •1324 0100.
- •4 Основы теории перечисления Пойа. Лемма Бернсайда.
- •Упражнения.
- •Глава. Основы схем из функциональных элементов.
- •1) Мультиплексор порядка
- •2) Дешифратор порядка .
- •3) Универсальный многополюсник.
- •Глава. Введение в теорию конечных автоматов.
- •Глава. Введение в теорию кодирования.
- •Теория кодирования.
Введение
В данном методическом пособии рассматриваются вопросы, входящие в университетский курс по дискретной математике. Большой раздел посвящён проблемам полноты булевых функций. В нём изложены основные определения и результаты по данной проблематике: теорема о представлении булевой функции в виде совершенной дизъюнктивной (конъюнктивной) нормальной формы, полинома Жегалкина, критерий Поста полноты, базисы в предполных классах. Следующий раздел посвящён проблемам минимизации представления булевых функций в виде ДНФ: геометрическая интерпретация, покрытия, интервалы, метод построения сокращённой и минимальных ДНФ. В заключение излагаются основы классического исчисления высказываний: основные определения, теорема дедукции, полнота исчисления высказываний.
Все разделы снабжены большим количеством учебных примеров и задач.
Пособие создано на основе программы первого семестра курса лекций по дискретной математике, читавшегося в Волгоградском государственном университете.
Дискретная математика
Булевой функцией f(x1 … xn) называют функцию, аргументы которой принимают значения из множества , и значение функции также из множества {0;1}.
1.Табличные способы задания булевых функций :
-
x1
…
xn
f(x1…xn)
0
…
0
*
0
…
1
*
…
…
…
…
1
…
1
*
В начале выписываются двоичные наборы из n нулей и единиц. Это удобно делать в двоичной системе счисления – то есть начиная с нуля прибавлять единицу в двоичной системе счисления. На каждом наборе надо задать значение функции.
Пример табличного задания функции:
-
x1
x2
x3
f(x1 x1 x3)
0
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
0
2.Основные булевые функции и их таблицы.
0 – константа ноль ;
1 – константа один ;
x - тождественная ;
![]() -
отрицание ;
-
отрицание ;
![]() -
конъюнкция (логическое умножение) ;
-
конъюнкция (логическое умножение) ;
![]() -
дизъюнкция (логическое сложение) ;
-
дизъюнкция (логическое сложение) ;
+ - модульная сумма ;
~ - эквивалентность (отрицание модульной суммы) ;
![]() -
следствие .
-
следствие .
|
x1 |
x2 |
0 |
1 |
x1 |
|
x1 |
x1 |
x1+ x2 |
x1 ~ x2 |
x1 |
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
3.Свойства булевых функций :
Определения.
Бинарная операция ассоциативна, если тождественно выполняется: ;
бинарная
операция коммутативна,
если тождественно выполняется:
![]() ;
;
бинарная
операция
![]() дистрибутивна по отношению к бинарной
операции
дистрибутивна по отношению к бинарной
операции
![]() ,
если тождественно выполняется:
,
если тождественно выполняется:
![]() ;
;
Утверждение
1.
![]() ,конъюнкция
ассоциативна.
,конъюнкция
ассоциативна.
|
x1 |
x2 |
x3 |
x2
|
x1 |
x1 |
(x1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Утверждение
2.
![]() ,
,
дизъюнкция ассоциативна.
|
x1 |
x2 |
x3 |
x2
|
x1
|
x1 |
(x1
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Утверждение
3.
![]() ,конъюнкция
,конъюнкция
коммутативна;
![]() ,
дизъюнкция также
,
дизъюнкция также
коммутативна;
-
x1
x2
x1
 x2
x2x2
 x1
x1
0
0
0
0
0
1
0
0
1
0
0
0
1
1
1
1
Предложение 1. Результат выполнения ассоциативной операции не зависит от расположения скобок в скобочном выражении.
Например:
Если
![]() ассоциативная операция, тогда
ассоциативная операция, тогда
![]() .
.
Доказательство предлагается в качестве домашнего упражнения.
Примечание: использовать индукцию по числу скобок в выражении.
Из того, что конъюнкции и дизъюнкции ассоциативные операции, результат конъюнкции или дизъюнкции нескольких переменных не зависит от расположения скобок.
Например:
![]()
Тогда
в силу независимости значения выражений
конъюнкций от расположения скобок
корректно определение
![]() как значение логического произведения
при каком-либо порядке расположения
скобок. Точно также для дизъюнкции
как значение логического произведения
при каком-либо порядке расположения
скобок. Точно также для дизъюнкции![]() .
.
Предложение
2.
Конъюнкция
![]() равна 0, т. и т.т., когда хотя бы один из
множителей
равна 0, т. и т.т., когда хотя бы один из
множителей![]() равен 0.
равен 0.
Дизъюнкция
![]() равна 1, т. и т.т., когда хотя бы одно из
слагаемых
равна 1, т. и т.т., когда хотя бы одно из
слагаемых![]() равно 1.
равно 1.
Доказательство предлагается в качестве домашнего упражнения.
Утверждение 4.
![]() ,
конъюнкция
дистрибутивна по отношению к дизъюнкции.
,
конъюнкция
дистрибутивна по отношению к дизъюнкции.
|
x1 |
x2 |
x3 |
x2
|
x1 |
x1 |
x1 |
(x1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Утверждение 5.
![]() ,
дизъюнкция
дистрибутивна по отношению к конъюнкции.
,
дизъюнкция
дистрибутивна по отношению к конъюнкции.
|
x1 |
x2 |
x3 |
x2 |
x1 |
x1 |
x1 |
(x1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Утверждение
6.
![]() ,
следствие не ассоциативная операция.
,
следствие не ассоциативная операция.
|
x1 |
x2 |
x3 |
x2 |
x1 |
x1 |
(x1 |
|
|
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Утверждение
7.
![]()
|
x1 |
x2 |
x3 |
x2 |
x1 |
x1+x2 |
x1+x3 |
(x1+x2) |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Утверждение 8.
![]() ,
,
конъюнкция дистрибутивна по отношению к сумме по модулю два.
|
x1 |
x2 |
x3 |
x2+x3 |
x1 |
x1 |
x1 |
(x1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
Определение. Две функции назовем одинаковыми, если они зависят от одного и того же набора переменных и их значения совпадают на каждом из наборов своих переменных.
Определение
Переменная x булевой функции f(x…) называется существенной, если существует набор значений остальных переменных функции, что изменение значения переменной при данном наборе остальных переменных изменяет значение функции.
Пример: x1 и x2 существенные переменные (x1 по 8 –му и по 5-му наборам; x2
по 6 и 8 наборам).
x3 не существенная переменная
|
x1 |
x2 |
x3 |
f |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
|
|
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Определение
Две функции равны, если они одинаковы после отбрасывания несущественных переменных.
Теорема:
Число различных (неодинаковых) булевых
функций от n переменных есть
![]() .
.
Теорема будет следовать из следующего утверждения:
число различных двоичных наборов длины n есть 2n (под длиной набора подразумевается число цифр в нем).
Докажем утверждение индукцией по длине n набора.
Для n=1 имеем 0;1 два различных набора длины 1;
21 =2. Для n=1 утверждение индукции справедливо.
Пусть утверждение индукции справедливо для n1, то есть число различных двоичных наборов длины n1 есть 2n.
Покажем справедливость утверждения для n=n+1. Разобьем все двоичные наборы длины n+1 на две группы. В первую группу отнесем двоичные наборы, которые начинаются на 0. Во вторую группу отнесем двоичные наборы, которые начинаются на 1, например, для n+1 = 3 будет такое разбиение:
-
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
Двоичные наборы первой (второй) группы получаются из всевозможных двоичных наборов длины n добавлением слева нуля (единицы) к всевозможным наборам длины n.
Но
по предположению индукции наборов длины
n имеется 2n,
поэтому число наборов как в первой, так
и во второй группе будет 2n,
поэтому общее число наборов длины (n+1)
будет 2n+2n
=
2n![]() 2
= 2n+1
2
= 2n+1
Утверждение доказано.
-
x1
…
xn
f(x1…xn)
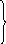 0
0…
0
*
2n
……
…
…
1
…
1
*
Функций от n переменных будет ровно столько, сколько существует разных двоичных наборов длины 2n.
По
предыдущему утверждению это число есть
![]() .
Теорема доказана.
.
Теорема доказана.
Определение :
Элементарной конъюнкцией на множестве переменных {x1…xn} называют функцию логического произведения множителей , где каждый множитель либо переменная, либо отрицание переменной.
В
дальнейшем значение
![]() в
элементарной конъюнкции будем опускать
или заменять
в
элементарной конъюнкции будем опускать
или заменять![]() .
.
Например: { x1 x2 x3 x4 }
x 1
x2
x4
;
эта функция равна 1, только на одном
наборе:
1
x2
x4
;
эта функция равна 1, только на одном
наборе:

 1 0 1 x1
1 0 1 x1
![]() x2
x2
![]() x4=1
x4=1
x1 x2 x4
Рангом
конъюнкции называют
число переменных конъюнкции. Далее
будем считать, что все переменные в
множителях элементарных конъюнкций
различны. В противном случае, используя
правила :![]() ,
приведем конъюнкции к нужном виду;
,
приведем конъюнкции к нужном виду;
Например:
![]()
полученная конъюнкция будет тождественно равна первоначальной.
В силу коммутативности и ассоциативности бинарной конъюнкции, две приведенные конъюнкции равны, т . и т. т., когда они состоят из одного набора множителей.
![]()
Определение
Элементарной дизъюнкцией на множестве переменных {x1…xn} называют функцию логического сложения слагаемых , где каждое слагаемое либо переменная, либо отрицание переменной.
Например:
{ x1
x2
x3
x4
![]()
 x1
x1
![]() x2
x2
![]() x4
;
эта функция равна 0, т. и т.т., когда все
слагаемые равны 0. т.е. на наборах 0110 и
0100
x4
;
эта функция равна 0, т. и т.т., когда все
слагаемые равны 0. т.е. на наборах 0110 и
0100
Рангом дизъюнкции называют число слагаемых дизъюнкции. Далее будем считать, что все переменные в множителях элементарных дизъюнкций различны . В противном случае , используя правила :
![]()
![]()
приведем дизъюнкции к нужном виду; полученная дизъюнкция будет тождественно равна первоначальной.
В силу коммутативности и ассоциативности элементарные дизъюнкции равны, т . и т. т., когда они состоят из одного и того же набора слагаемых.
Дизъюнктивной нормальной формой (ДНФ) на множестве переменных (x1…xn) называют функцию логического сложения некоторых слагаемых, где каждое слагаемое есть элементарная конъюнкция на (x1…xn) :
{ x1 x2 x3 x4 }
![]()
ДНФ называется совершенной (СДНФ), если каждая элементарная конъюнкция имеет ранг n :
![]()
Далее считаем, что слагаемые ДНФ не повторяются (в противном случае можно
Множество единиц ДНФ есть объединение множества единиц элементарных конъюнкций ДНФ. Каждая элементарная конъюнкция полного ранга имеет единственную единицу. Слагаемые СДНФ (элементарные конъюнкции полного ранга) и единицы СДНФ находятся во взаимнооднозначном соответствии.
Теорема о представлении любой булевой функции в виде СДНФ : для любой булевой функции справедлива следующая формула :
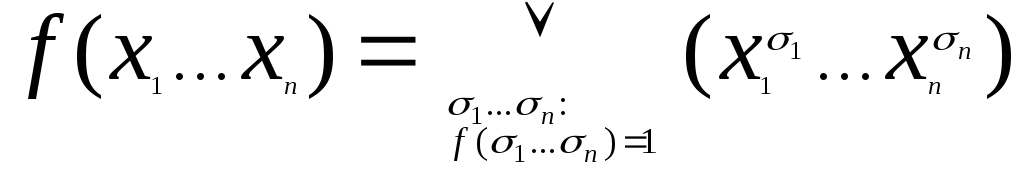
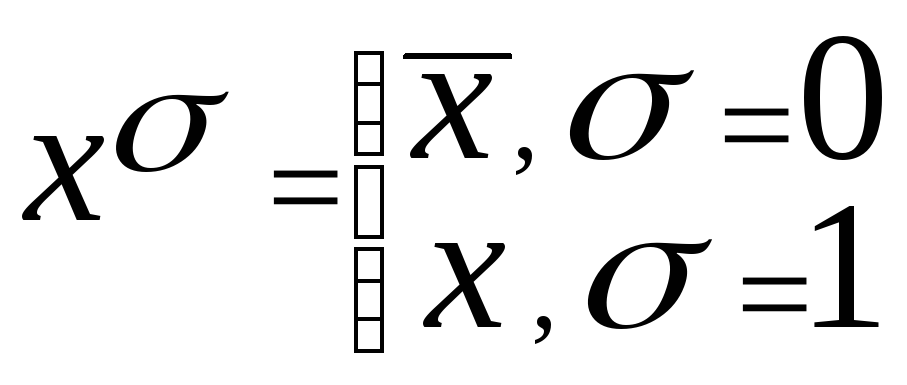
-
x1
x2
x3
f
0
0
0
0
0
0
1
0
0

1
0
1
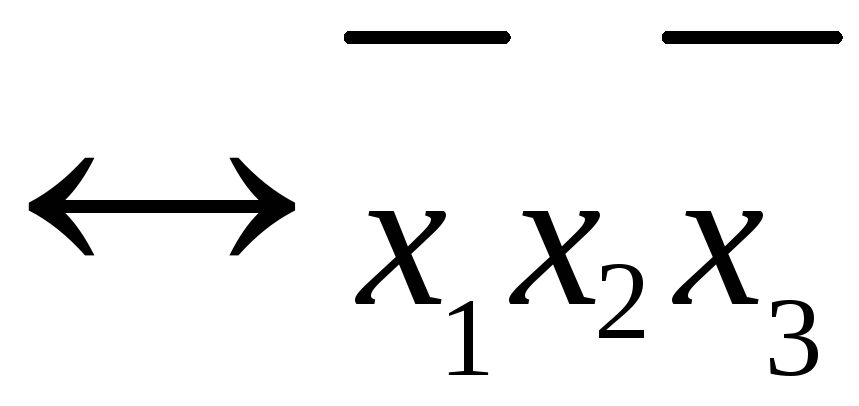
0
1
1
0
1
0
0
1
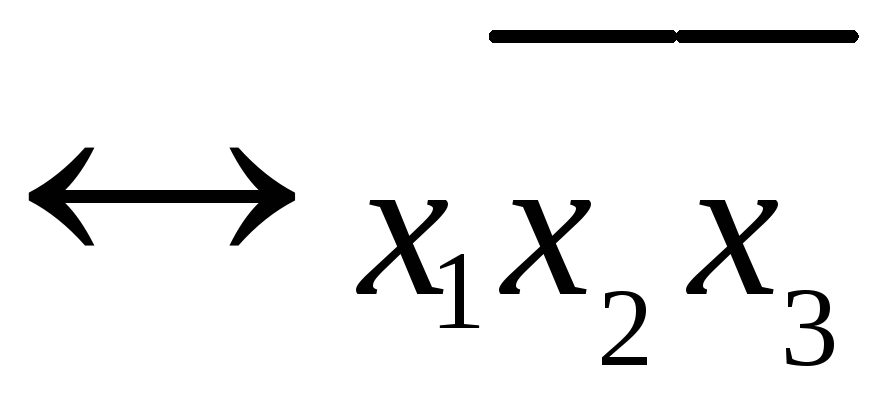
1


0
1
1
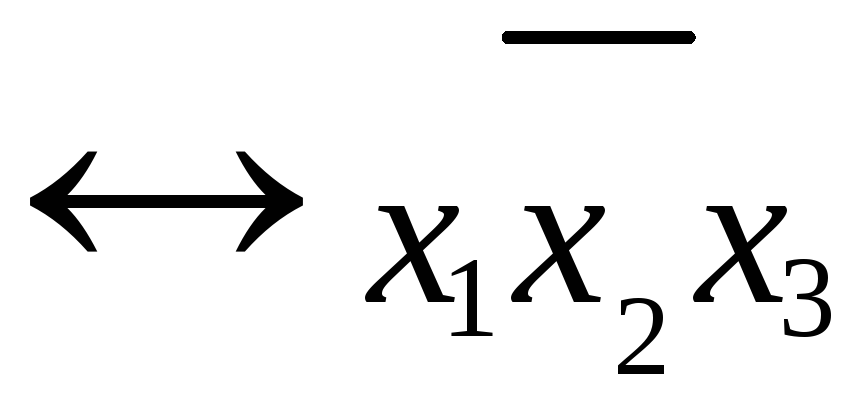
1
1
0
0
1
1
1
0
![]()
Доказательство:
Свойства
![]()
![]()
1)
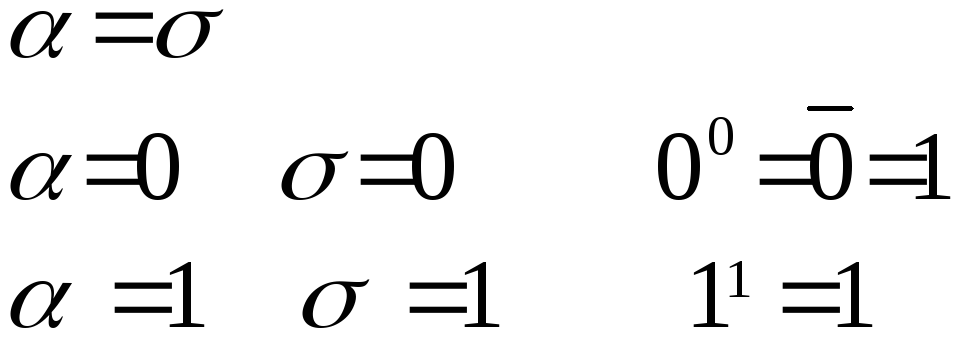
2)
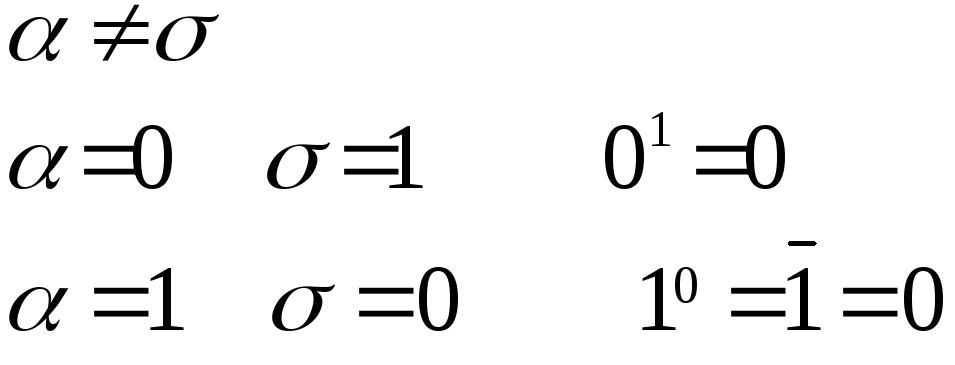
Чтобы доказать теорему покажем выполнение данного равенства на любом двоичном наборе ,то есть что левые и правые части совпадают для любого двоиного набора:
![]() .
.
![]() .
То есть левая часть равенства равна 1.
Покажем,что и правая часть равенства
также равна 1 на данном наборе. Для этого
достаточно показать,что хотя бы одно
слагаемое правой части равно 1.
.
То есть левая часть равенства равна 1.
Покажем,что и правая часть равенства
также равна 1 на данном наборе. Для этого
достаточно показать,что хотя бы одно
слагаемое правой части равно 1.
Таким слагаемым будет слагаемое, которое соответствует единичному набору , совпадающего с набором .
![]() .
.
Значение
этого слагаемого на наборе
![]() есть
есть
![]() в
силу того ,что значение каждого множителя
равно 1. Последнее справедливо в силу
свойства символа
в
силу того ,что значение каждого множителя
равно 1. Последнее справедливо в силу
свойства символа
![]() .
.
![]() .
То есть левая часть равна 0. Покажем, что
и правая часть также равна 0. Для этого
нужно показать, что значение всех
слагаемых равно 0. Рассмотрим произвольное
слагаемое правой части, которое
соответствует некоторому двоичному
набору
.
То есть левая часть равна 0. Покажем, что
и правая часть также равна 0. Для этого
нужно показать, что значение всех
слагаемых равно 0. Рассмотрим произвольное
слагаемое правой части, которое
соответствует некоторому двоичному
набору
![]() ,
тогда
,
тогда![]() в силу, того, что наборы
и
различны, т.к.
- набор, на котором значение функции
равно 0, а
- набор, на котором значение функции
равно 1. Так как наборы различны, то
существует множитель i:
в силу, того, что наборы
и
различны, т.к.
- набор, на котором значение функции
равно 0, а
- набор, на котором значение функции
равно 1. Так как наборы различны, то
существует множитель i:
![]() ,
а поэтому и все произведение равно
0.Таким образом каждое слагаемое равно
0, следовательно и вся сумма равна 0,
значит правая часть равна 0.
,
а поэтому и все произведение равно
0.Таким образом каждое слагаемое равно
0, следовательно и вся сумма равна 0,
значит правая часть равна 0.
Теорема полностью доказана.
|
x1 |
x2 |
x3 |
f |
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
Теорема о разложении булевой функции по первым k-переменным.
![]()
Доказательство:
Рассмотрим
произвольный набор значений переменных
![]() ,
и покажем, что левая и правая часть
равны. Левая часть -
,
и покажем, что левая и правая часть
равны. Левая часть -![]() .
.
В
правой части рассмотрим слагаемое, в
котором значение набора
совпадает с первыми k-компонентами
набора :
![]() .
.
Значение
этого слагаемого на наборе
![]() равно
равно![]() .
.
В
силу того, что набор
и первые k-компонент набора
совпадают, рассматриваемые множители
равны 1, все слагаемое равно
![]() .
Все остальные слагаемые равны 0 в силу
того, что среди множителей
.
Все остальные слагаемые равны 0 в силу
того, что среди множителей![]() обязательно найдется множитель, в
котором
и
различаются, а это нулевой множитель.
Поэтому правая часть равна
обязательно найдется множитель, в
котором
и
различаются, а это нулевой множитель.
Поэтому правая часть равна
![]() (все слагаемые, кроме быть может одного,
равны 0).
(все слагаемые, кроме быть может одного,
равны 0).
Теорема доказана.
Нетрудно убедиться в справедливости следующих тождеств:
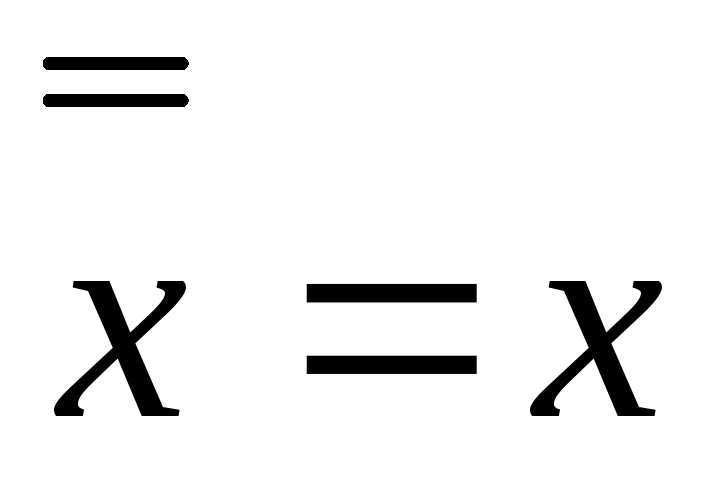 6)
6)
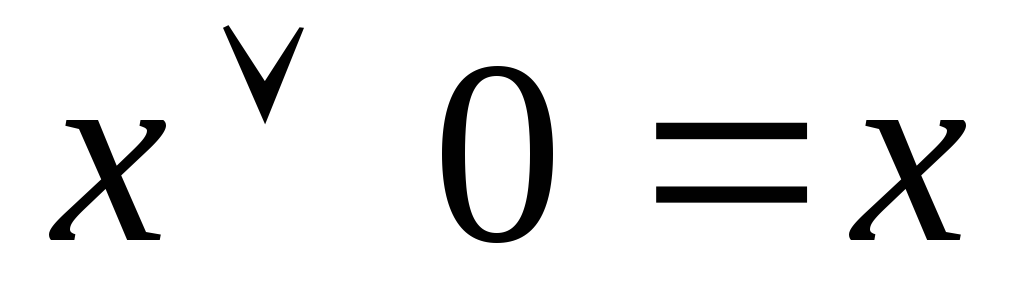
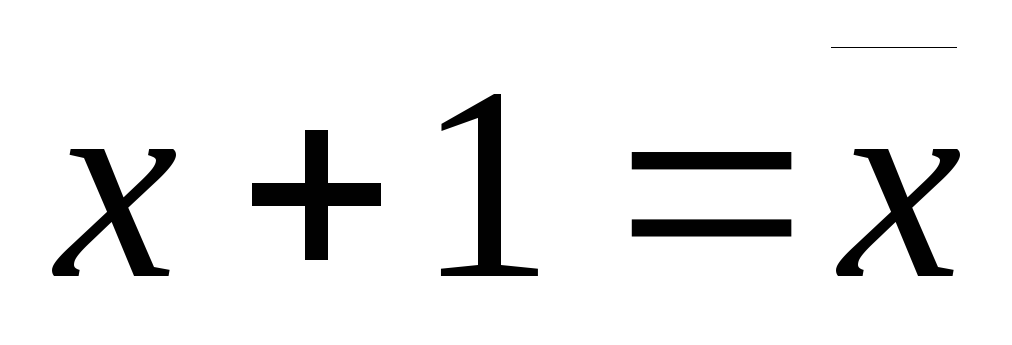 7)
7)

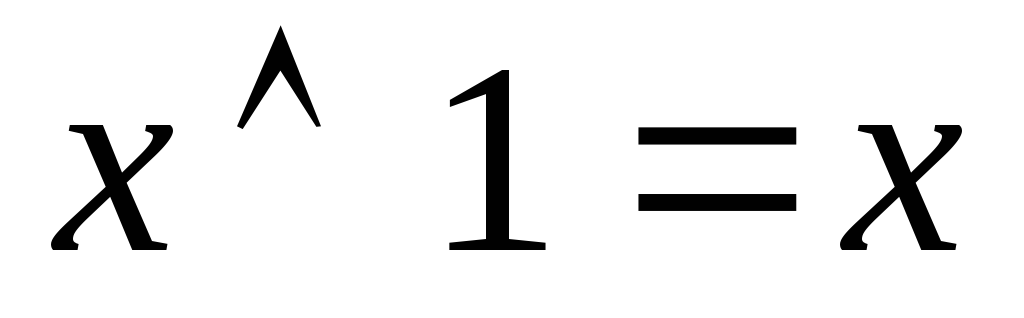 8)
8)
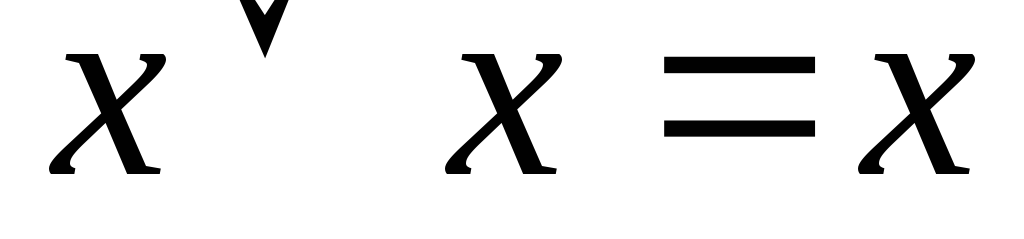
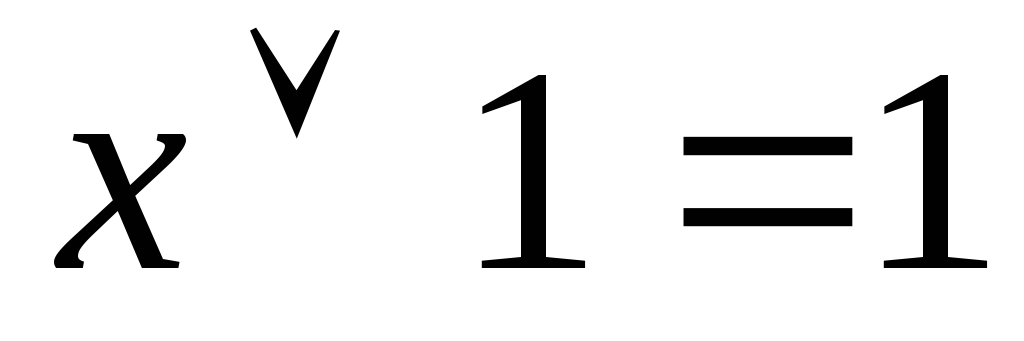 9)
9)
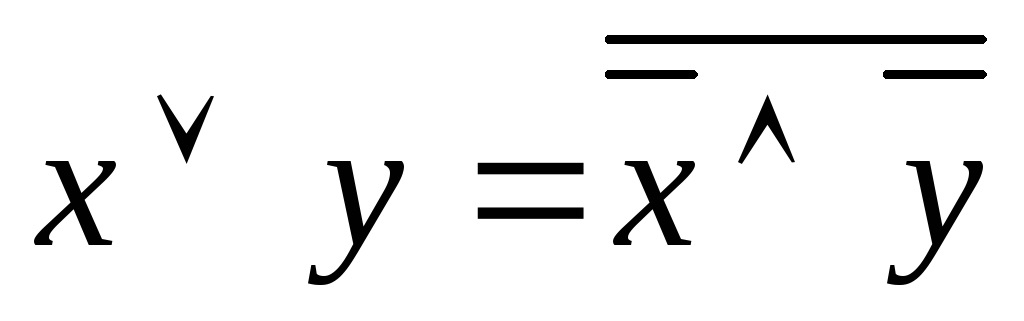
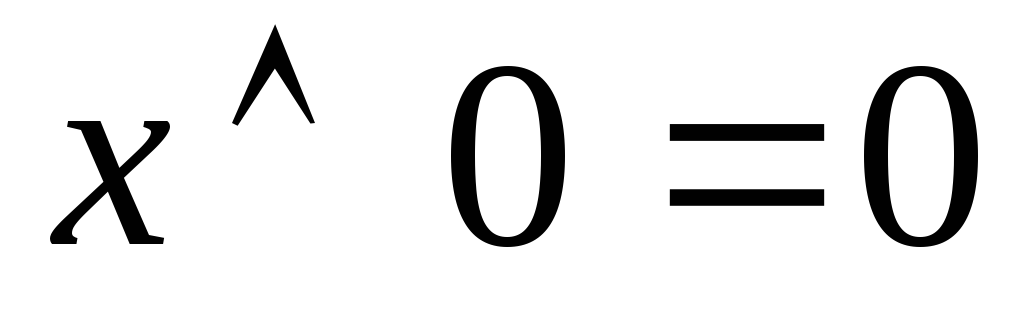 10)
10)
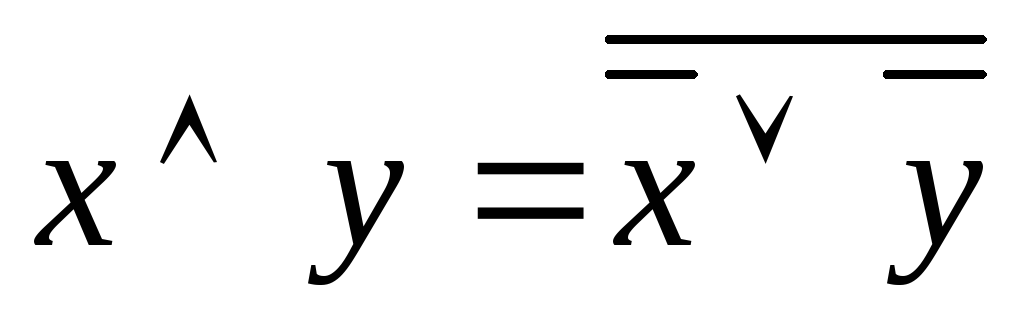
Доказательство предлагается в качестве домашних упражнений.
Последние два тождества называются правилами Де-Моргана.
Определение.
Двойственной
к функции
![]() называют функцию
называют функцию
![]() .
.
Например, двойственной к конъюнкции является
дизъюнкция, и наоборот, двойственной к дизъюнкции является конъюнкция.
![]()
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 1
Утверждение.
Двойственной
к двойственной функции есть сама функция,
т.е.
![]()
![]()
Теорема о представлении булевой функции в виде конъюнктивной нормальной формы .
КНФ называют логическое произведение некоторых сомножителей, где каждый сомножитель есть элементарная дизъюнкция. КНФ от переменных {x1…xn} называется СКНФ, если каждая дизъюнкция полного ранга, то есть в каждую дизъюнкцию входят все n переменных.
Пример: { x1 x2 x3 }
КНФ
:
![]()
СКНФ:
![]()
Теорема о представлении любой булевой функции в виде СКНФ.
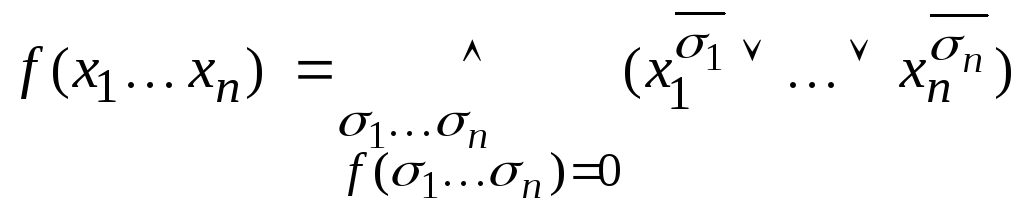
Пример:
-
x1
x2
f
0

0
0
0
1
1
1

0
0
1

1
0
![]()

Доказательство
: рассмотрим произвольный набор значений
переменных
![]() .
Либо
.
Либо![]() ,
либо
,
либо![]() .
.
Левая часть равенства равна 1. Покажем, что и правая часть равна единице. Рассмотрим произвольный множитель правой части
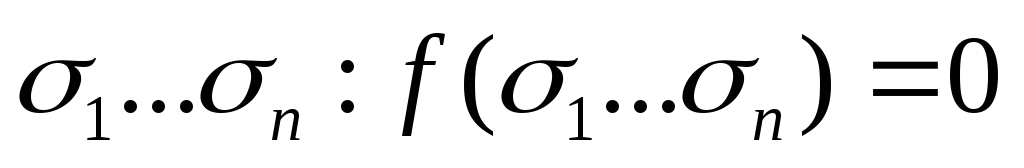 .
Значение этого множителя на наборе
.
Значение этого множителя на наборе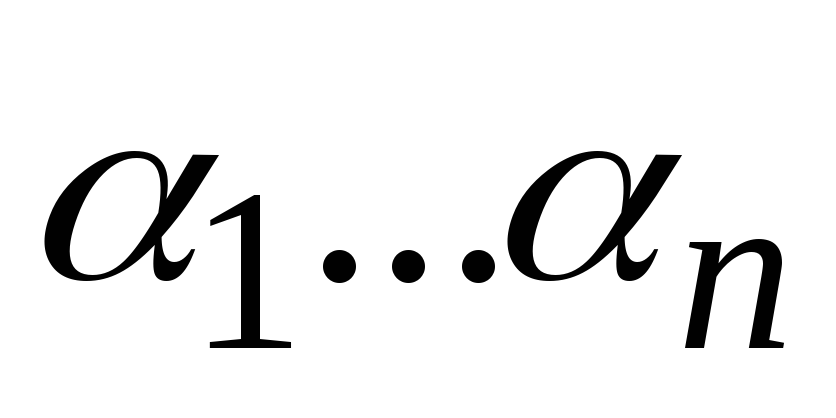 равно
равно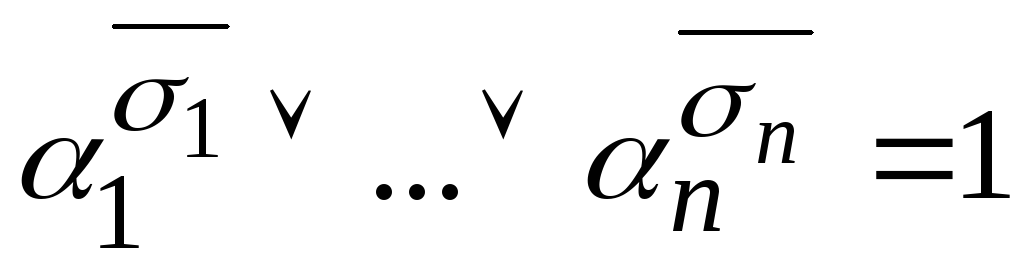 т.к. существует i такое, что
т.к. существует i такое, что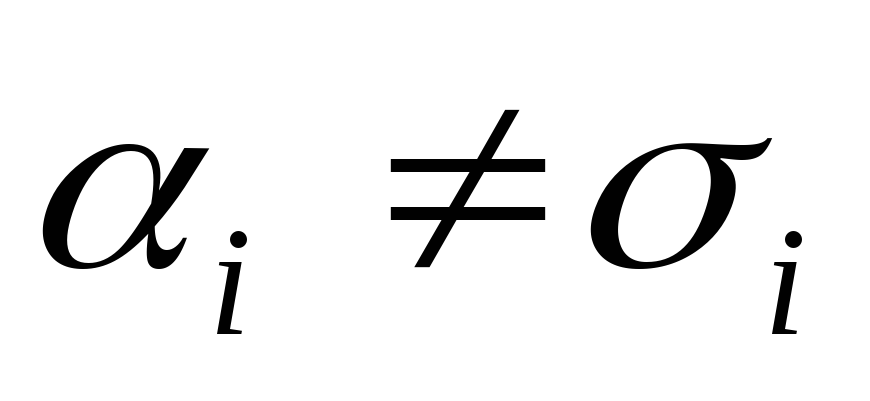 , что верно в силу того, что
- набор, на котором значение f ()
= 1, а
- набор, на котором значение f()=
0, то есть
и
- два различных набора, а поэтому есть
компонента, в которой они отличаются.
, что верно в силу того, что
- набор, на котором значение f ()
= 1, а
- набор, на котором значение f()=
0, то есть
и
- два различных набора, а поэтому есть
компонента, в которой они отличаются.
Поэтому
![]() ; т.к.
; т.к.![]() ,
,![]() .
.
Пусть
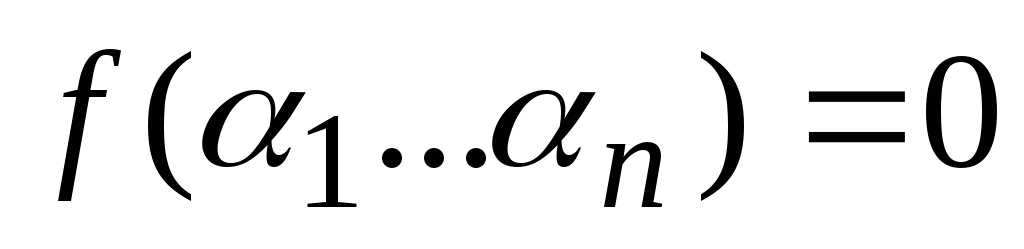 .
Покажем, что и правая часть равна 0. Для
этого достаточно показать, что существует
множитель, который равен 0 на наборе.
Действительно, рассмотрим множитель
соответствующий набору правой части
.
Покажем, что и правая часть равна 0. Для
этого достаточно показать, что существует
множитель, который равен 0 на наборе.
Действительно, рассмотрим множитель
соответствующий набору правой части
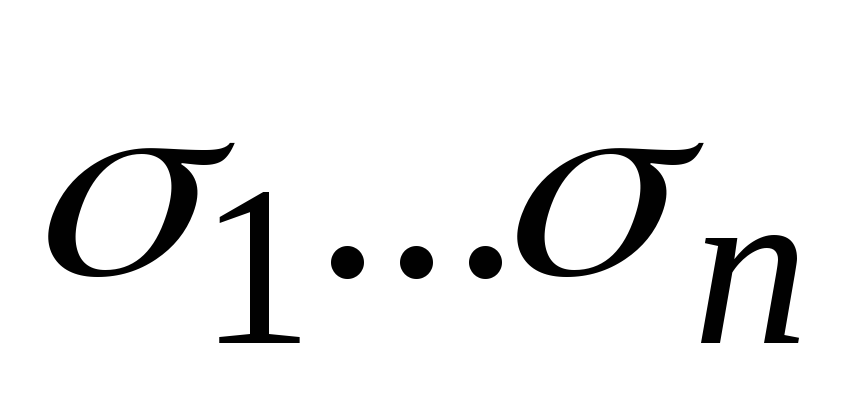 ,
который совпадает с набором
,
который совпадает с набором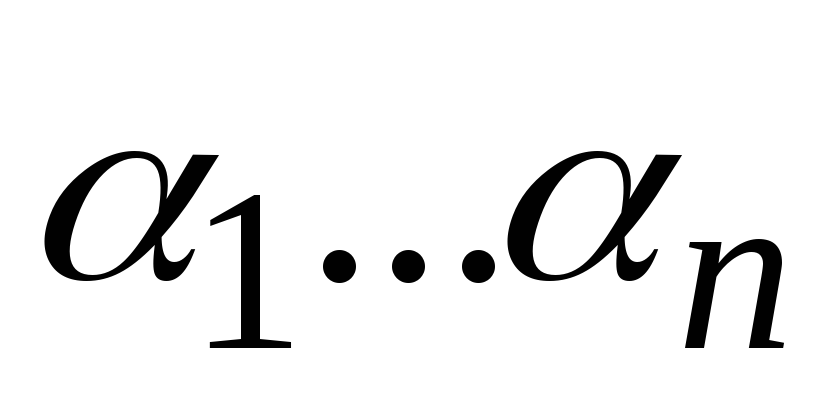 .
.
В
силу того, что
![]() есть ноль функции, набор
есть ноль функции, набор![]() существует. Тогда значение рассматриваемого
множителя на наборе
равно
существует. Тогда значение рассматриваемого
множителя на наборе
равно
![]()
(т.
к.![]() для
всех i :
для
всех i :![]() ).
А так как существует множитель, равный
0, то и значение всей СКНФ = 0.
).
А так как существует множитель, равный
0, то и значение всей СКНФ = 0.
Теорема о разложении булевой функции по первым k переменным .
Для любой булевой функции f(x1…xn) тождественно выполнено :
![]()
Доказательство.
Рассмотрим произвольный набор
![]() .
Значение левой части есть
.
Значение левой части есть![]() .
.
В
правой части множитель, в котором
![]() будет
равен 1 в силу того, что
будет
равен 1 в силу того, что![]() ,
тогда
,
тогда![]() в силу того, что
в силу того, что![]() ,
а раз некоторое слагаемое равно 1 , вся
элементарная дизъюнкция равна 1. Тогда
остается один множитель
,
а раз некоторое слагаемое равно 1 , вся
элементарная дизъюнкция равна 1. Тогда
остается один множитель![]() ,
который равен
,
который равен
![]()
Тогда
все произведение есть
![]() .
Что и требовалось доказать.
.
Что и требовалось доказать.
Замечание Используя понятие двойственности, можно показать справедливость предыдущих утверждений о КНФ непосредственным сведением к утверждениям о ДНФ. В разделе о суперпозиции функций будет приведено данное доказательство.
Определение : Полиномом Жегалкина называется сумма по модулю 2 (+) некоторого количества слагаемых, где каждое слагаемое есть элементарная конъюнкция переменных без отрицания.
Пример:
1+x1x2+x3+x1x4x5
Полином Жегалкина, не содержащий ни одного слагаемого, равен 0.
Далее будем рассматривать так называемые приведенные полиномы Жегалкина, т.е. полиномы, в которых все слагаемые различные конъюнкции.
Например 1+x1x2+x3+x1x4x5 (нет двух одинаковых слагаемых).
Если некоторые слагаемые повторяются, то используя правило x+x=0, нетрудно привести любой полином к приведенному виду.
Н
 апример
x1x2+x3+x1x2+x1x4x5+x3=x1x4x5
апример
x1x2+x3+x1x2+x1x4x5+x3=x1x4x5
Если слагаемое повторяется нечетное количество раз, то оставляем его в единственном экземпляре.
Теорема о представлении булевой функции в виде полинома Жегалкина .
Для любой булевой функции существует представление в виде полинома Жегалкина и это представление единственно.
Доказательство:
Пример 1:
-
x1
x2
x3
0
0
0
0
0
0
1
0
0
1
0
1
0

1
1
0
1
0
0
0
1
0
1
1
1

1
0
0
1
1
1
0
Первая
часть теоремы следует из теоремы о
представлении булевой функции в виде
СДНФ. А именно рассмотрим для булевой
функции ее СДНФ. Далее операцию
![]() выразим через операцию
выразим через операцию![]() по правилу Де Моргана
по правилу Де Моргана![]() .
.
После
чего операцию
![]() выразим через операцию
выразим через операцию![]() и приведем полученную формулу к
нормальному виду полинома Жегалкина
раскрыв скобки в полученном выражении,
используя дистрибутивность конъюнкции
по отношению к сумме по модулю два. Для
функции из примера1 СДНФ имеет вид :
и приведем полученную формулу к
нормальному виду полинома Жегалкина
раскрыв скобки в полученном выражении,
используя дистрибутивность конъюнкции
по отношению к сумме по модулю два. Для
функции из примера1 СДНФ имеет вид :
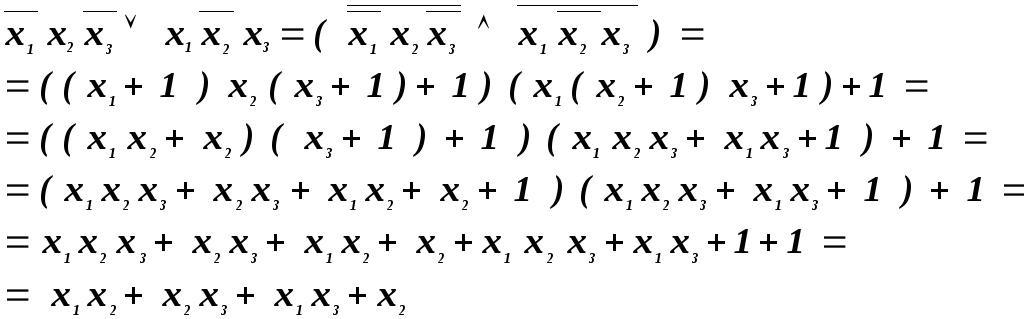
Покажем, что полученный полином единственен с точностью до перестановки слагаемых и множителей в слагаемых полинома.
Допустим
противное :
![]() ,
которая имеет два различных полинома
Жегалкина:
,
которая имеет два различных полинома
Жегалкина:
![]()
Из этих равенств следует,что
![]()
прибавим
к обеим частям равенства
![]() :
:
![]()
В
силу того, что
![]() и
и![]() различные полиномы Жегалкина, либо в
различные полиномы Жегалкина, либо в![]() есть слагаемое, которого нет в
есть слагаемое, которого нет в![]() ,
либо наоборот. Поэтому приведенный
полином
,
либо наоборот. Поэтому приведенный
полином![]() отличен по форме от нуля
отличен по форме от нуля![]() ,
т.е. в этом полиноме присутствуют
слагаемые, не тождественно равные нулю,
и полином тождественно равен константе
ноль :
,
т.е. в этом полиноме присутствуют
слагаемые, не тождественно равные нулю,
и полином тождественно равен константе
ноль :![]() .
.
Далее
рассмотрим слагаемое полинома
![]() ,
содержащее наименьшее число переменных.
Теперь рассмотрим набор значений
переменных, в котором переменные данного
слагаемого равны 1, а все остальные
переменные равны 0. Тогда, нетрудно
видеть, что значение
,
содержащее наименьшее число переменных.
Теперь рассмотрим набор значений
переменных, в котором переменные данного
слагаемого равны 1, а все остальные
переменные равны 0. Тогда, нетрудно
видеть, что значение![]() на таком наборе равно 1 (в полиноме будет
ровно 1 только одно слагаемое с наименьшим
числом переменных, остальные обязательно
содержат нулевой множитель, поэтому
равны 0), в то время как
на таком наборе равно 1 (в полиноме будет
ровно 1 только одно слагаемое с наименьшим
числом переменных, остальные обязательно
содержат нулевой множитель, поэтому
равны 0), в то время как![]() на всех наборах. Противоречие.
на всех наборах. Противоречие.
Упражнение: найдите полином Жегалкина следующих функций :
1)
![]() 4)
4)
![]()
2)
![]() 5)
5)
![]()
3)
![]() 6)
6)
![]()
Упражнение
Покажите справедливость формулы для любой двоичной функции f справедливо разложение
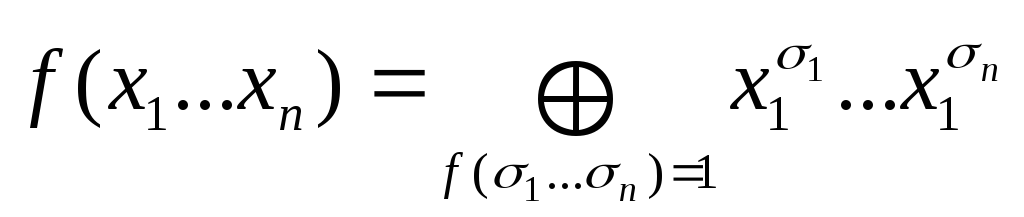 л
л
Т.е в формуле представления функции в виде СДНФ можно заменить логическое суммирование на суммирование по модуля 2.
Определение
Пусть
![]() – конечное множество. Отношением на
данном множестве будем называть любое
подмножество его декартового
произведения
– конечное множество. Отношением на
данном множестве будем называть любое
подмножество его декартового
произведения![]() .
.
Рассмотрим
декартово произведение ![]() на себя:
на себя: ![]() .
Т.е. это множество всевозможных слов из
двух букв в алфавите
.
Т.е. это множество всевозможных слов из
двух букв в алфавите ![]() .
.
Определение
Отношением
эквивалентности ![]() называется подмножество декартового
произведения, которое удовлетворяет
следующих трем свойствам:
называется подмножество декартового
произведения, которое удовлетворяет
следующих трем свойствам:
Рефлексивность.
 .
.Симметричность.
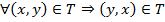 .
.Транзитивность.
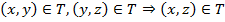 .
.
Примеры отношения эквивалентности.
Пример
1.
Рассмотрим в качестве множества X
множество натуральных чисел: ![]() .
Для него рассмотрим обычное равенство
натуральных чисел. Скажем, что два
натуральных числа эквивалентны, если
они равны в обычном смысле. Очевидно,
что это есть отношение эквивалентности.
.
Для него рассмотрим обычное равенство
натуральных чисел. Скажем, что два
натуральных числа эквивалентны, если
они равны в обычном смысле. Очевидно,
что это есть отношение эквивалентности.
Пример
2.
Рассмотрим произвольное натуральное
число ![]() .
Числа x
и y
назовем эквивалентными
.
Числа x
и y
назовем эквивалентными ![]() ,
если они дают один и тот же остаток при
делении на
,
если они дают один и тот же остаток при
делении на ![]() .
Очевидно, что это есть отношение
эквивалентности.
.
Очевидно, что это есть отношение
эквивалентности.
Пример
3.
Введем отношение эквивалентности на
множестве слов, длина которых не меньше
числа ![]() .
Рассмотрим множество этих слов в алфавите
.
Рассмотрим множество этих слов в алфавите
![]() .
Скажем, что пара слов
.
Скажем, что пара слов ![]() и
и ![]() эквивалентны, если совпадают их первые
эквивалентны, если совпадают их первые
![]() букв. Убедитесь сами, что все три свойства
эквивалентности выполнены.
букв. Убедитесь сами, что все три свойства
эквивалентности выполнены.
Утверждение.
Пусть ![]() – множество,
– множество, ![]() – отношение эквивалентности на нем.
Тогда
– отношение эквивалентности на нем.
Тогда ![]() разбивает все элементы
разбивает все элементы ![]() на классы эквивалентных элементов
на классы эквивалентных элементов ![]() (Любая пара различных классов не
пересекается между собой-
(Любая пара различных классов не
пересекается между собой-![]() ,
и их объединение совпадает с множеством
,
и их объединение совпадает с множеством![]() ;
;![]() ;
количество классов может быть бесконечным).
Любая пара элементов одного класса
эквивалентна, а любая пара элементов
различных классов не эквивалентна.
Данное разбиение однозначно определяется
отношением эквивалентности
;
количество классов может быть бесконечным).
Любая пара элементов одного класса
эквивалентна, а любая пара элементов
различных классов не эквивалентна.
Данное разбиение однозначно определяется
отношением эквивалентности ![]() .
.
Доказательство данного утвнрждения предлагается в качестве самостоятельного упражнения.
Определение: суперпозицией булевых функции
![]()
называется функция
![]() ,
полученная путем подстановки
,
полученная путем подстановки
функции![]() в
функцию
в
функцию![]() вместо
некоторой переменной:
вместо
некоторой переменной:![]() .
.
Замечание 1
Множества переменных подставляемых функций могут пересекаться.
Замечание 2
Переименование
переменных есть частный случай
суперпозиций :
![]() ,
в которой вместо
,
в которой вместо![]() подставлена функция
подставлена функция![]() ,
то есть
,
то есть![]() переименованна в
переименованна в![]() .
.
Определение
Будем различать переименование двух видов:
переименование с отождествлением, как в предыдущем примере (переменная переименуется в другую переменную этойже функции );
переименование без отождествления (когда переменная получает наименование, которого нет среди переменных функции).
Определение
Две функции назовем эквивалентными, если одну из другой можно получить переименованием переменных без отождествления.
Например
эквивалентны![]() и
и![]() .
.
Функции
![]() и
и
![]() не
эквивалентны, так как эквивалентные
функции имеют одинаковое число
существенных переменных.
не
эквивалентны, так как эквивалентные
функции имеют одинаковое число
существенных переменных.
Утверждение Двойственная суперпозиции функций- есть суперпозиция двойственных.
![]()
Доказательство
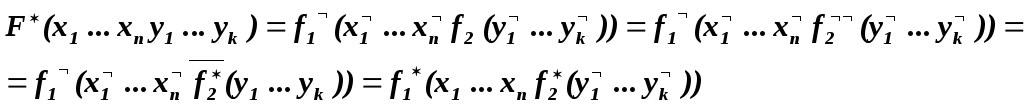
Тогда утверждение о представлении функции в виде СКНФ непосредственно следует из аналогичного утверждения о представлении функции в виде СДНФ.
Теорема о представлении любой булевой функции в виде СКНФ.
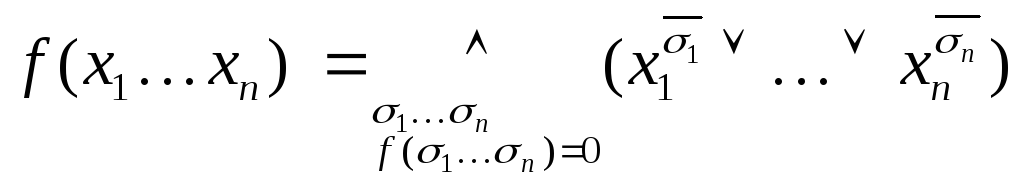
Теорема о представлении любой булевой функции в виде СДНФ : для любой булевой функции справедлива следующая формула :
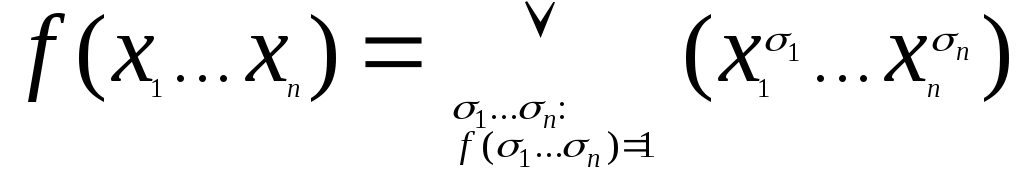
Чтобы
провести это сведение возьмем двойственную
функцию ![]()
и представим ее в виде СДНФ:
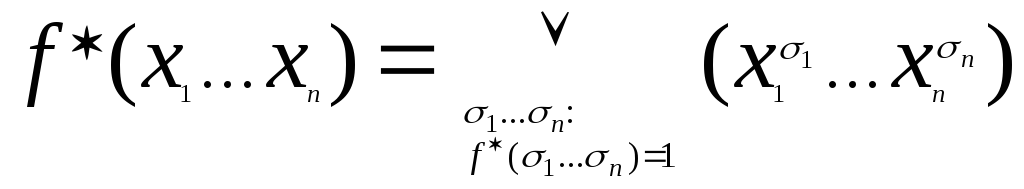 ,
тогда
справедливы выкладки:
,
тогда
справедливы выкладки:
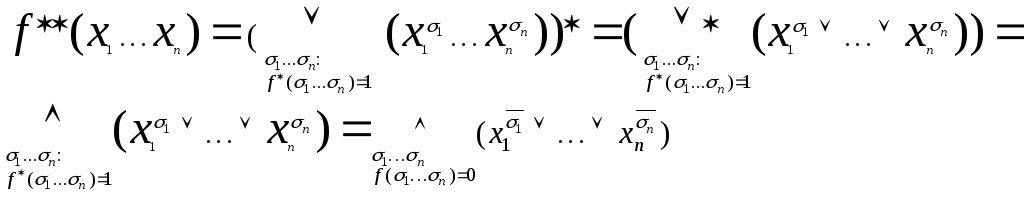
Последнее
равенство справедливо в силу того, что
противоположные наборы к нулям функции
![]() -
есть единицы двойственной функции
-
есть единицы двойственной функции![]() .Используя
ранее полученное тождество
.Используя
ранее полученное тождество =
=![]() ,
получаем требуемое разложение.
,
получаем требуемое разложение.
Замечание 3
Введеное отношение между функциями является отношением эквивалентности, и поэтому по основному утверждению разбивает все множество функций на классы эквивалентных функций- любая пара функций из одного и тогоже класса эквивалентны между собой, а любая пара функций из разных классов между собой не эквивалентны.
Замечание 3
В дальнейшем будем рассматривать функции с точностью до эквивалентности. То есть под функцией будем понимать класс эквивалентных фукций, в который входит данная функция.
Определение:
замыканием
системы
функций![]() называется множество функций
называется множество функций![]() ,
полученных из функций
,
полученных из функций![]() всевозможными суперпозициями.
всевозможными суперпозициями.
Пример
1: ![]()
![]()
Здесь принимается обозначение: слева от стрелки стоит исходная функция, над стрелкой – какая функция и вместо какой переменной исходной фукции производится подстановка, справа от стрелки результат подстановки.
Пример
2:
![]()
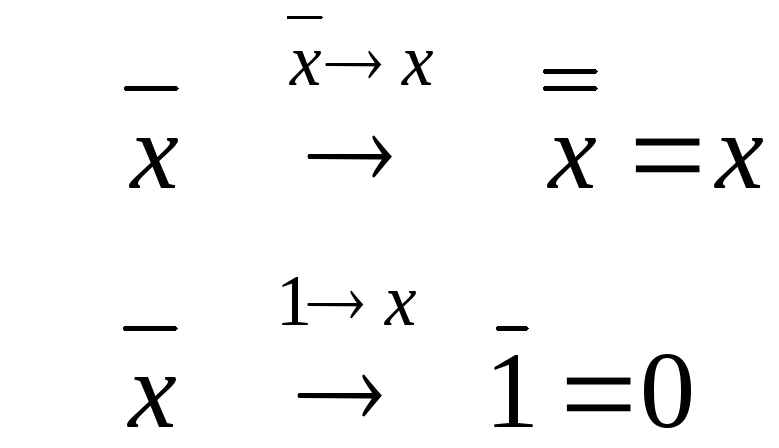
Упражнение
Покажите, что остальные подстановки не дают новых функций в указанных примерах.
Определение
:
замкнутой
системой функции называют систему,
замыкание которой совпадает с самой
системой
![]() .
.
Пример
3:
![]()
Определение: система функций называется полной, если ее замыкание совпадает с классом всех булевых функций.(По другому говоря, с помощью суперпозиций функций из системы можно получить любую булевую функцию.)

 0
0 1
1