ГидравликаВиВ

МИНИСТЕРСТВО ОБРАЗОВАНИЯИ НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ИЖЕВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ГИДРАВЛИКА

Курс лекций Учебно-методическое пособие для специальности 290800

Ижевск

2004

ВВЕДЕНИЕ

Гидравлика – прикладная инженерная наука, в которой изучаются законы равновесия и движения жидкостей, а также методы применения этих законов для решения технических задач.

Развитие гидравлики шло двумя параллельными путями. Первый путь – теоретический, когда с помощью математического анализа решаются задачи механики жидкости как непрерывно деформируемой сплошной среды.

Вопросами теоретического анализа занимается теоретическая гидромеханика. Необходимо, однако, отметить, что решение многих задач гидромеханики чрезвычайно сложно; как правило, оно сводится к уравнениям в частных производных, имеющим решения лишь в ограниченном количестве случаев.

Второй путь – экспериментальный. На этом пути получено большое количество ценных результатов в тех случаях, когда теоретическое решение задач на сегодняшнем уровне развития гидромеханики вообще невозможно.

Внастоящее время происходит интенсивное развитие гидравлики по обоим направлениям. Применение ЭВМ во много раз расширяет возможности теоретического решения проблем гидродинамики; с другой стороны, появление новой высокоточной аппаратуры и новых, совершенных методик эксперимента увеличивает возможности эксперимента в решении задач гидравлики и поиске оптимальных инженерных решений.

Современные города невозможно представить без развитых гидравлических систем тепло - и водоснабжения, водоотведения. Расчет и проектирование этих систем, а также гидротехнических сооружений, гидротурбин, гидроприводов основаны на закономерностях гидромеханики

Гидравлика как наука начала развиваться в далёкой древности. Известный закон Архимеда о силе, действующей на погружённое в жидкость тело (250г. до н.э.), дошёл до наших дней. После этого, вплоть до работы Леонардо да Винчи «О движении и измерении воды», работ в области гидравлики не появлялось. Последующее развитие гидравлики началось в 16−17 веках. Сюда относятся работы Г. Галилея «О телах, пребывающих в воде», голландского учёного Стевина «Начало гидростатики», Э. Торичелли – об истечении жидкости, Б. Кастелли – о движении жидкости в каналах, Б. Паскаля, сформулировавшего закон о передаче давления в жидкости;

И. Ньютона, впервые изложившего основы внутреннего трения в жидкости и установившего закон динамического подобия.

Всамостоятельную науку гидравлика сформировалась только после работ, выполненных Д. Бернулли и Л. Эйлером в Российской академии наук. В своём труде «Гидродинамика» (1738) Д. Бернулли получил широко известное уравнение, являющееся основным уравнением гидравлики. Л. Эйлер в работе «Общие признаки движения жидкости» (1755) вывел дифференциальные уравнения равновесия и движения жидкостей.

Большой вклад в гидравлику внесли французские учёные А. Шези,

А. Дарси, Л. Навье, немецкие учёные Л. Прандтль, Т. Карман, Г. Шлихтинг, англичане У.Фруд, О. Рейнольдс, Дж. Стокс и другие.

Из отечественных учёных следует отметить И.С. Громеко − основателя изучения вихревого движения жидкости. Н.П. Петров опубликовал работу «Гидродинамическая теория трения при наличии смазывающей жидкости» (1882), принёсшую ему мировую известность. В.Г. Шухов в 1886 г. выполнил исследования движения вязких жидкостей (в приложении к нефти).

Великий русский учёный Н.Е. Жуковский в 1898 г. решил задачу о гидравлическом ударе в трубах, создал теорию фильтрации подземных вод, совместно с С.А.Чаплыгиным развил теорию Н.П. Петрова гидродинамической смазки подшипника, разработал теорию подъемной силы крыла, применяемую в авиации и для расчета рабочих колёс турбин и насосов.

А.Н. Крылов и С.О. Макаров создали теорию устойчивости и незатопляемости кораблей. Л.С. Лейбензон создал теорию движения вязких жидкостей, Н.Н. Павловский предложил метод решения фильтрационных задач, основанный на гидродинамических аналогиях (ЭГДА).

Работы М.В. Келдыша, М.А. Лаврентьева, Л.И. Седова, Л.Г. Лойцянского, А.Н. Колмогорова и др. явились основополагающими для многих современных направлений гидромеханики.

Врезультате содружества науки и производства гидравлика превратилась

впередовую практическую науку. В НИИ и ВУЗах выполняются исследовательские работы по дальнейшему развитию гидромеханики и созданию новых, более совершенных устройств и сооружений инженерной гидравлики.

1. ОСНОВНЫЕ ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ

При изучении жидкостей гидравлика абстрагируется от дискретного строения вещества, рассматривая жидкость как сплошную среду, параметры которой изменяются непрерывно. Это позволяет применять математический аппарат, используемый при исследовании непрерывных функций.

Жидкости, изучаемые гидравликой, делят на капельные (малосжимаемые) и газообразные (сжимаемые). В состоянии покоя и при движении с малыми скоростями газы подчиняются тем же законам, что и капельные жидкости (например, при движении воздуха в вентиляционных каналах).

Соотношение между ρ и γ легко получить из формулы:

Здесь g − ускорение свободного падения.

Сжимаемость жидкости характеризуется модулем сжимаемости βp , определяемым из соотношения:

Здесь W− начальный объем жидкости, ΔW − изменение объема, Δp − из− менение давления. Знак минус в формуле (1.4) объясняется тем, что ΔW и Δp

всегда имеют разные знаки. Для воды βp = 5∙10− 8 Па−1. При давлениях до 10 МПа сжимаемостью жидкости можно пренебречь и считать ее практически несжимаемой. Величина, обратная модулю сжимаемости, называется модулем упругости Е и имеет размерность Па.

Температурное расширение жидкости при нагреве характеризуется коэффициентом объемного расширения βT, определяемым из формулы:

Здесь Т − приращение температуры. Для воды βT = 0,00015 1/град. Вязкость жидкости − ее способность сопротивляться сдвигу. При

движении жидкости между ее слоями возникают внутренние силы – силы трения, создающие касательные напряжения.

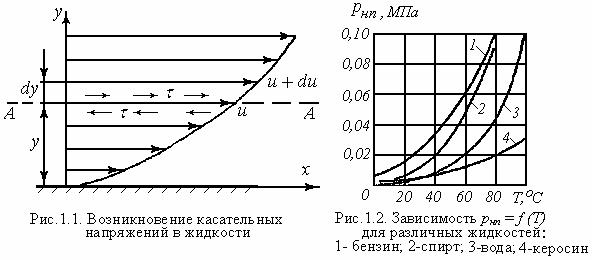
Рассмотрим движение жидкости вдоль стенки (рис. 1.1).

Из рисунка видно, что по мере удаления от стенки скорости жидкости возрастают. Это объясняется тем, что каждый нижележащий слой тормозит движение вышележащего. На стенке скорость равна нулю из-за прилипания частиц жидкости к стенке. Кривая распределения скоростей по сечению потока называется эпюрой скоростей.

Применим известный в механике метод сечений − на расстоянии у от стенки проведем секущую плоскость А−А , отделяющую верхнюю часть потока

от нижней. Отбросим нижнюю часть потока и заменим ее силами, с которой она действует на верхнюю. Это будут тормозящие силы трения, распределенные по секущей плоскости (касательные напряжения τ). Эти напряжения, согласно гипотезе Ньютона, пропорциональны поперечному градиенту скорости du/dy и определяются формулой:

В этой формуле коэффициент пропорциональности μ имеет численное значение, характерное для данной жидкости. Он называется динамическим коэффициентом вязкости и имеет размерность Па∙с. Например, для воды при Т=20оС и атмосферном давлении μ = 0,00101 Па∙с.

Для характеристики вязкости применяется также кинематический коэффициент вязкости ν, определяемый из соотношения ν = μ / ρ. Его размерность в системе СИ − м2/с. Применяются также дольные единицы: 1Стокс = 1 см2/с (Ст) и 1сантистокс (1сСт), равный 0,01Ст. Для воды при Т=20оС и атмосферном давлении ν = 1,01 сСт (1,01∙10-6 м2/с).

При повышении температуры вязкость капельных жидкостей (коэффи− енты μ и ν ) падает. Влияние давления на вязкость капельные жидкостей незначительно.

Следствие из гипотезы Ньютона : при u = 0 du = 0 и τ =0. Это означает, что в покоящейся жидкости касательные напряжения отсутствуют.

Жидкости, подчиняющиеся гипотезе Ньютона, называются ньютоновскими. Подавляющее большинство жидкостей, применяемых в технике − ньютоновские. Гидравлика изучает именно такие жидкости.

Испаряемость жидкостей характеризуется давлением насыщенного пара pнп , Па. Оно устанавливается в закрытом сосуде с жидкостью после предварительной откачки из него воздуха. Давление насыщенного пара – функция температуры (рис. 1.2). Если давление газа над жидкостью равно давлению насыщенного пара при данной температуре, в жидкости начинается процесс кипения. Например, для воды при Т=20оС pнп= 2400 Па , при 100оС давление насыщенного пара равно атмосферному.

Растворимость газа в жидкости определяется законом Генри:

Здесь Wж − объем жидкости, Wг − объем газа, растворенный в этом объеме жидкости (приведенный к нормальным условиям), pг − абсолютное давление газа над жидкостью, pа − величина атмосферного давления, к − безразмерная константа Генри. Величина к характеризует растворимость газа в жидкости и зависит от вида жидкости. Например, для воды к = 0,016, керосина 0,13, минеральных масел 0,08.

Особые свойства воды заключаются в следующем:

1. Все жидкости при нагревании расширяются, и с повышением температуры их плотность падает. Вода же при нагреве от 0 до +4оС не

расширяется, а сжимается, и плотность ее растет. При дальнейшем повышении температуры вода начинает расширяться, и вплоть до 100оС плотность ее убывает. Таким образом, она имеет наибольшую плотность при +4оС. В водоемах зимой у дна благодаря этому поддерживается постоянная температура +4оС, что способствует выживанию живых организмов.

2.У всех жидкостей при замерзании образующееся твердое вещество тонет в жидкости, так как имеет плотность выше, чем у нее. Плотность льда, образующегося при замерзании воды, наоборот, ниже, чем у воды, и лед плавает на поверхности водоема. Имея низкий коэффициент теплопроводности, слой льда предохраняет водоем от полного промерзания (разумеется, при достаточно большой его глубине). Это также способствует сохранению жизни в водоеме зимой.

3.Вода имеет очень высокую удельную теплоемкость по сравнению с другими жидкостями. Это делает ее весьма выгодным энергоносителем.

4.Вода меняет свои свойства под воздействием магнитного поля. Магнитная обработка воды снижает образование накипи в котельных установках, ускоряет твердение бетона.

В ряде случаев гидравлика использует понятие идеальной жидкости. Идеальная жидкость – это упрощенная математическая модель жидкости. Она считается абсолютно невязкой и несжимаемой.

2. ГИДРОСТАТИКА

Гидростатика − раздел гидравлики, изучающий закономерности, которым подчиняются жидкости, находящиеся в состоянии покоя. Последний может быть «абсолютным» (когда жидкость неподвижна относительно Земли) и отно− сительным (когда она неподвижна относительно сосуда, но сосуд обладает переносным движением).

2.1. Силы, действующие в жидкости

Вследствие своей текучести (подвижности частиц) жидкость не может сопротивляться действию сосредоточенных сил. В ней могут действовать только силы, распределенные либо по массе (массовые), либо по поверхности (поверхностные).

К массовым силам относятся силы собственного веса и силы инерции

переносного движения. Единичной массовой силой Rmназывается массовая сила, действующая на единицу массы, или Rm Rm / M . Физический смысл единичной массовой силы − ускорение, вызванное этой силой. Проекции этого ускорения на координатные оси обозначаются X, Y, Z. Если речь идет об элементарной массе dM, то на нее действует такое же ускорение, как и на всю массу М. Следовательно, можно записать:

Поверхностные силы действуют на границах выделенного объема жидкости со стороны жидкости, окружающей данный объем. Для выявления поверхностных сил применим метод сечений (рис. 2.1).

В выделенном объеме возьмем точку А и проведем через нее секущую плоскость, делящую объем на две части. Отбросим часть 1 и заменим ее силами, действующими со стороны объема 1 на объем 2. Эти силы распределены по секущей поверхности. В окрестности точки А рассмотрим элементарную площадку dF. На нее действует силаdR . Разложим ее на две составляющие − нормальную к площадке dN и касательную dT . Обозначим

Здесь σ − нормальное напряжение, τ− касательное напряжение. Нормальное напряжение сжатия в жидкости называют давлением. В случае покоя жидкости касательные напряжения отсутствуют.

Давление в покоящейся жидкости называется гидростатическим. Оно обладает двумя свойствами:

а) на границах выделенного объема жидкости силы, вызванные давлением, направлены по нормали внутрь рассматриваемого объема. Это объясняется тем, что жидкость практически неспособна сопротивляться растягивающим силам и может работать только на сжатие.

б) величина давления в данной точке объема не зависит от пространственной ориентации площадки dF.

Докажем последнее свойство. Выделим в жидкости элементарный объём в виде тетраэдра с рёбрами ∆x, ∆y, ∆z (рис. 2.2).

Пусть на жидкость внутри выделенного объёма действует единичная массовая сила, составляющие которой равны X,Y,Z. Под воздействием сил, действующих на грани тетраэдра, и массовой силы он находится в равновесии.

Масса тетраэдра равна произведению его объёма на плотность:

Уравнение равновесия в проекции на ось x имеет вид:

сравнению с первым и со вторым, пропадёт, а px, py, pz, pn остаются. В итоге из этих трех уравнений получаем: px= py= pz= pn .

Так как. направления осей были взяты произвольно, то по любым направлениям давление в точке будет одинаково. Поэтому гидростатическое давление можно рассматривать как скалярную величину. Таким же свойством обладает давление в движущейся идеальной жидкости.

2.2. Дифференциальные уравнения равновесия жидкости

Возьмём в покоящейся жидкости точку D с координатами x,y,z и выделим при ней элементарный объём в виде прямоугольного параллелепипеда со сторонами dx, dy, dz (рис. 2.3). Его объем равен dxdydz, а масса − dxdydz.

На выделенный элемент действует массовая сила dRm и поверхностные силы давления, направленные нормально к граням внутрь объема.

Составим уравнение равновесия объема в проекции на ось х. Будем считать, что по бесконечно малой площадке давление распределено равномерно

направленную противоположно оси x.

Единичная массовая сила, действующая в жидкости, имеет составляющие X,Y,Z. Проекция массовой силы dRm на ось х будет равна dxdydzX .

Итак, уравнение равновесия в проекции на ось х запишется в виде:

Открыв скобки, сократив на не равное нулю произведение dxdydz и разделив

на ρ, получим: X 1 p 0. Аналогично выглядят проекции уравнения

x

равновесия на другие оси. В итоге получим систему дифференциальных уравнений равновесия (уравнений Эйлера), имеющую вид:

Для решения этой системы сведём её к одному уравнению. Для этого умножим первое на dx, второе на dy, третье на dz и сложим все три уравнения.

Трёхчлен в скобках – полный дифференциал давления dp. В итоге получим:

Это уравнение также является дифференциальным уравнением равновесия. Оно может быть решено, если известны проекции единичных массовых сил X,Y,Z.

Запишем последнее уравнение в виде ( Xdx Ydy Zdz ) dp. Поскольку жидкость рассматриваем как несжимаемую (ρ=const), то уравнение имеет смысл, если выражение в скобках представляет собой полный дифференциал, как и правая часть. Для этого необходимо, чтобы существовала некоторая функция U(x,y,z), частные производные от которой равнялись бы проекциям X,Y,Z , то - есть должны существовать равенства:

Функцию U можно назвать силовой или потенциальной. Так как массовые силы пропорциональны создаваемым ими ускорениям X,Y,Z, то их называют силами, имеющими потенциал.

Введем понятие поверхности равного давления. Это поверхность , проведенная в жидкости так, что на ней давление постоянно (p = const, dp=0).

Уравнение равновесия будет для нее иметь вид:

Это и есть уравнение поверхности равного давления. Из аналитической геометрии известно, что это – условие перпендикулярности двух векторов с проекциями dx,dy,dz и X,Y,Z. Поскольку dx,dy,dz − проекции отрезка, лежащего на поверхности равного давления, а X,Y,Z − проекции результирующей единичной массовой силы, то можно сделать вывод: поверхность равного

давления перпендикулярна направлению результирующего ускорения от массовых сил, действующих в жидкости.