ГидравликаВиВ

4.10. Турбулентный режим движения

Характерным признаком турбулентного движения является преобладающее действие динамических сил, во много раз превосходящих силы вязкости. Это происходит при больших числах Re, когда движение становится неустойчивым и случайные возмущения не могут гаситься силами вязкости.

Вначале на некоторых участках ламинарного течения возникают отдельные турбулентные «облачка»; затем, при возрастании скорости, они превращаются в турбулентные «пробки», занимающие все сечение трубы (такая турбулентность называется перемежающейся); при еще большем повышении скорости наступает полностью развитый турбулентный режим.

Измерения скорости и давления в турбулентном потоке показывают, что они непрерывно пульсируют. Если расположить датчик, непрерывно измеряющий мгновенную скорость (например, в направлении продольной оси х), в какой-либо фиксированной точке потока, то запись его показаний по времени выглядит так, как показано на рис. 4.15. Мгновенная скорость u при этом складывается из осредненной составляющей скорости u и

пульсационной составляющей u .

Линии тока в турбулентном потоке, как уже указывалось, расположены неупорядоченно; они пересекаются между собой, вызывая перемешивание слоев жидкости. В потоке наблюдаются вихревые области, возникающие в различных местах и вновь исчезающие (рис. 4.16).

Так как при турбулентном режиме происходит изменение параметров движения по времени, оно является неустановившимся. Исследования, однако, показывают, что если осредненные скорости в точках потока по времени не меняются, поток условно можно считать установившимся и применять к нему уравнение Бернулли.

Эпюра скоростей турбулентного потока в трубе значительно отличается от эпюры при ламинарном режиме (рис. 4.17).

Центральная часть сечения А, где осредненные скорости изменяются слабо, называется ядром турбулентного потока. Примыкающая к стенке кольцевая зона В, где происходит резкое нарастание скорости от нуля до скорости в ядре, называется пристенным слоем. Непосредственно у стенки имеется очень тонкий слой δ, где движение жидкости близко к ламинарному. Его называют вязким подслоем (некоторые авторы называют его ламинарной

пленкой). Толщина вязкого подслоя весьма мала и составляет 0,001 – 0.3 мм. Более ровный характер эпюры скоростей в турбулентном потоке объясняется обменом кинетической энергией между слоями жидкости при перемешивании. Коэффициент Кориолиса α зависит от числа Re и изменяется

в пределах от 1,13 при Re Reкр до 1.025 при Re 3 106. При практических

расчетах принимают α = 1.

В трубопроводах систем отопления, вентиляции, теплоснабжения, водоснабжения, газоснабжения режим движения, как правило, турбулентный, так как движущаяся среда (вода, пар, воздух, газ) имеют малую вязкость. Так, для газопроводов домовой сети числа Re бывают не ниже 3000, в городских сетях − не ниже 200 000; в вентиляционных системах − не ниже 150 000; в сетях сжатого воздуха − не ниже 400 000; в паропроводах центрального отопления − не ниже 30 000, в паропроводах ТЭЦ достигают

3∙106 −5∙106.

Длина начального участка после входа в трубу, на которой происходит формирование эпюры осредненных скоростей, слабо зависит от числа Re и не превышает (40 – 50)d.

4.11. Дифференциальные уравнения движения Рейнольдса

Использовать уравнения Навье−Стокса для турбулентного движения нельзя, так как пульсационные составляющие скорости вносят весьма ощутимые изменения в энергию движущейся жидкости.

Введем осредненные и пульсационные скорости и давления: ux ux ux, p p p .

Рассматриваем установившееся турбулентное движение, поэтому:

Среднее значение пульсационных составляющих скорости и давления

ux 0, p 0, так как они могут быть как положительными, так и отрицательными. Среднее значение квадрата пульсационной составляющей

uxux 0, среднее значение произведений разноименных пульсационных составляющих uxuy также не равно нулю.

Выражая в уравнениях Навье−Стокса проекции скорости и их производные через осредненные и пульсационные составляющие и применяя

правила осреднения, после ряда алгебраических преобразований можно получить:

Это и есть дифференциальные уравнения движения Рейнольдса. Дополнением к этой системе служит уравнение неразрывности:

уравнениях Навье−Стокса) фигурируют p, uy , uz , ux ; кроме того, имеется

ряд членов с пульсационными составляющими. Они выражают действие дополнительных напряжений в жидкости, присущих только турбулентному потоку. Член uiu j / x, например, можно представить как uiu j / x .

Произведения вида uiu j называются турбулентными напряжениями.

Замыкание системы (установление дополнительных соотношений между турбулентными напряжениями и другими переменными, входящими в систему) − весьма трудная задача. Для некоторых случаев ее решали многие ученые (Л. Прандтль, Ж. Буссинеск, Т. Карман, Дж. Тэйлор и др.), вводя различные гипотезы и используя экспериментальные данные.

Впоследнее время появились принципиально новые подходы к изучению турбулентности, основанные на идеях А.Н.Колмогорова и использующие теорию вероятности и статистические методы.

5.ПРИКЛАДНЫЕ ЗАДАЧИ ГИДРОДИНАМИКИ

5.1.Путевые потери при турбулентном режиме

Вотличие от ламинарного режима, зависимости для определения гидравлических потерь, в том числе путевых, базируются исключительно на экспериментальных данных. Опыты показывают, что путевые потери при турбулентном режиме могут зависеть в общем случае от числа Рейнольдса и шероховатости трубы.

Шероховатость характеризуется двумя параметрами: абсолютной шероховатостью (средней высотой бугорков на внутренней поверхности

трубы) и относительной шероховатостью / d .

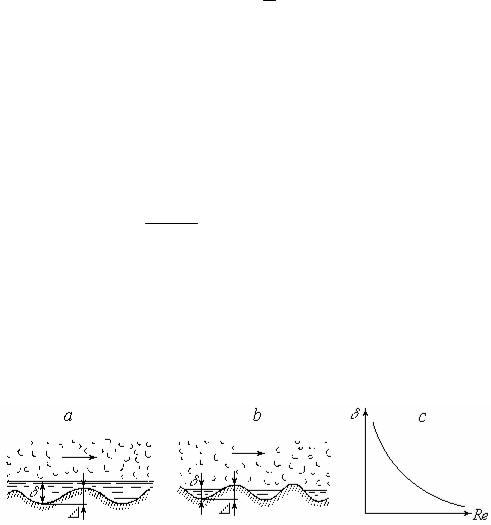
Как указывалось ранее, при турбулентном режиме у стенки имеется вязкий подслой толщиной . Если толщина этого подслоя (рис. 5.1, а), то выступы закрыты вязкой пленкой и в турбулентном пристенном слое жидкость, двигаясь, скользит по вязкому подслою как по жидкой смазке (по аналогии с ламинарным режимом).

Такая труба называется гидравлически гладкой.

В этом случае коэффициент сопротивления трения λ не зависит от шероховатости трубы и рассчитывается по формуле Блазиуса:

Если (рис. 5.1, b), труба называется гидравлически шероховатой.

У такой трубы бугорки шероховатости проходят сквозь вязкий подслой и оказываются в турбулентном потоке. При этом с бугорков срываются вихри, увеличивая гидравлические потери. Коэффициент λ при этом должен зависеть как от числа Re, так и от эквивалентной шероховатости трубы .

Рис.5.1. К определению гидравлически гладких и шероховатых труб

Толщина вязкого подслоя уменьшается с увеличением числа Re

(рис. 5.1, с). Поэтому одна и та же труба при различных числах Re может быть либо гидравлически гладкой, либо гидравлически шероховатой.

Следует отметить, что в трубах с естественной шероховатостью величина бугорков шероховатости различна. Большую роль, кроме величины абсолютной шероховатости, играет также форма бугорков, их густота и характер взаимного расположения на поверхности. Эти факторы учесть и выразить какими−либо формульными зависимостями практически невозможно.

Существенный вклад в этом направлении был внесен работами И.Никурадзе (1933 г.). Он проводил опыты на трубах с искусственной шероховатостью, наклеивая на внутреннюю поверхность труб равномерным слоем песчинки одного размера (полученные многократным просеиванием через сита). Относительная шероховатость при этом изменялась от 0,00197 до 0,066. В опытах измерялся расход жидкости и путевые потери на мерном участке трубы, после чего определялись число Re и коэффициент λ .

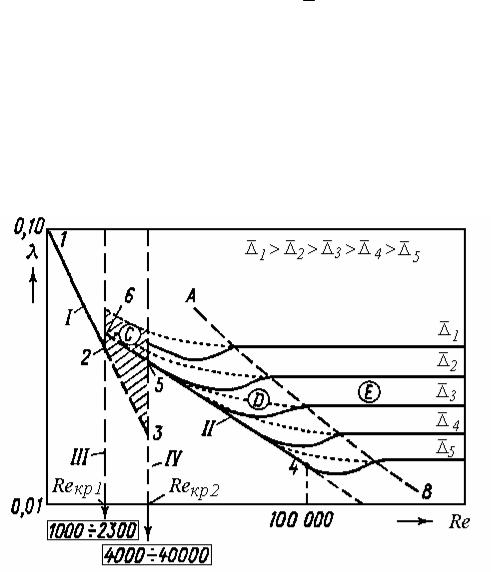
Результаты своих опытов И. Никурадзе нанес на график f(Re), построенный в логарифмических координатах (рис.5.2). На этом же графике изображены зависимости, соответствующие формуле Хагена – Пуазейля (для ламинарного режима) и Блазиуса (для гидравлически гладких труб при турбулентном режиме). В логарифмических координатах они представляют собой прямые линии.

На рис.5.2 линия I соответствует формуле Хагена–Пуазейля; II − формуле Блазиуса; III и IV − границам переходного режима.

Результаты опытов Никурадзе на этом графике изображены в виде кривых, расположенных правее линии II. Каждая кривая соответствует

определенной относительной шероховатости . Как видно из графика, опытные кривые при увеличении числа Re отходят от линии II, образуя «ложку»: вначале λ уменьшается, а потом начинает расти, выходя на постоянный уровень. Линия АВ на графике отделяет зону, где опытные кривые идут горизонтально.

На графике Никурадзе можно выделить несколько характерных областей.

Область линейного сопротивления соответствует линии I от точки 1 до точки 2. В этом интервале чисел Re путевые потери линейно зависят от скорости V. Покажем это.

Рис.5.2. График Никурадзе

Область переходного режима С (на графике заштрихована). Для этой области экспериментальные данные, полученные разными авторами, противоречивы; надежных формул для определения λ в этой области нет. Поэтому при проведении практических расчетов принято считать, что при Re Reкр1 скачком происходит переход к турбулентному режиму.

Область доквадратичного сопротивления соответствует кривой II.

В этой области наблюдается степенная зависимость путевых потерь от скорости V, причем показатель степени меньше двух . Покажем это.

Область шероховатых труб соответствует зоне D. Здесь величина λ зависит как от числа Re, так и от относительной шероховатости . Чем больше , тем раньше опытные кривые отходят от кривой Блазиуса. Это объясняется тем, что отход начинается, когда при увеличении числа Рейнольдса толщина вязкого подслоя сравняется с высотой бугорков шероховатости; они начинают при дальнейшем увеличении числа Re выступать из−под вязкого подслоя, увеличивая потери.

Область вполне шероховатых труб (область квадратичного сопротивления) − это область правее линии АВ. Здесь величина λ зависит только от и не зависит от числа Рейнольдса. (эта область называется еще автомодельной). Путевые потери зависят в этой области от квадрата скорости:

Результаты, полученные Никурадзе, позволили приводить естественную разнородную шероховатость труб к некоторой стандартной форме и ввести понятие эквивалентной шероховатости. Эквивалентной шероховатостьюэ называется такая равномерная зернистая шероховатость («шероховатость

Никурадзе»), которая дает одинаковую с естественной шероховатостью данной трубы величину λ. Для определения э не нужно производить каких−либо обмеров шероховатости − ее определяют путем гидравлических испытаний.

Гидравлические испытания труб с естественной шероховатостью, проведенные Колбруком, Г.А.Муриным, Ф.А.Шевелевым и рядом других авторов, показали, что у таких труб переход от кривой Блазиуса к кривой для гидравлически шероховатых труб происходит более плавно, без «ложки» (рис. 5.2, пунктирные кривые). Это объясняется тем, что при уменьшении толщины вязкого подслоя с увеличением числа Re бугорки искусственной шероховатости показываются из−под подслоя одновременно, так как все они имеют одинаковую высоту. Поэтому изменение λ происходит резко. В трубах с естественной шероховатостью все бугорки имеют различную высоту; их выход

из−под вязкого подслоя происходит постепенно. Поэтому λ изменяется более плавно.

Для гидравлически шероховатых труб (зона D) с естественной шероховатостью коэффициент λ может быть рассчитан по формуле Альтшуля:

Применение формул (5.1) либо (5.2) определяется следующим образом: Если 2300 Re 10d / э , труба считается гидравлически гладкой и

применяется фррмула Блазиуса.

Если 10d / э Re 500d / э, труба − гидравлически шероховатая и применяется формула Альтшуля.

Если Re 500d / э , труба называется вполне шероховатой. Это условие достигается при очень больших числах Re, когда в формуле Альтшуля можно пренебречь вторым слагаемым в скобках и получить формулу:

Эта формула называется формулой Шифринсона. Как следует из нее, в данном случае λ не зависит от числа Рейнольдса, а зависит только от относительной шероховатости трубы. Такое течение, при котором сохраняется независимость от какого−либо критерия подобия, называется автомодельным.

При практическом определении величины эквивалентной шероховатости трубу подвергают гидравлическим испытаниям − пропускают через нее жидкость и по расходу и величине потерь определяют Re и λ. Опыты проводят при больших расходах, чтобы полученное значение λ попало в область автомодельности. Зная d и λ, по формуле Шифринсона можно найти величину

ý, которая и заносится в гидравлические справочники, например:

−цельнотянутые новые стальные трубы – 0,01 − 0,1;

−цельнотянутые стальные трубы, находящиеся в эксплуатации – 1,2−1,5;

−цельнотянутые стальные паропроводы перегретого пара − 1,0;

−цельносварные новые стальные трубы – 0,04 – 0,1 и т.д.

5.2. Местные потери

Для определения местных потерь необходимо знать коэффициент местного сопротивления ζ и среднюю скорость для подстановки в формулу Вейсбаха (4.30). В качестве средней скорости V обычно берется скорость в трубопроводе до местного сопротивления; если берется скорость после сопротивления, это обязательно оговаривается. Если на трубопроводе имеется несколько местных сопротивлений, потери в них суммируются. Суммирование допускается только в случае, если расстояние между соседними местными сопротивлениями не превышает (40 – 60)d. При этом считается, что взаимное

влияние местных сопротивлений отсутствует (имеются данные о том, что длина участка взаимного влияния зависит от числа Re и шероховатости трубы).

При меньшем расстоянии соседние местные сопротивления считаются одним сопротивлением; коэффициент ζ для него определяется опытным путем.

При турбулентном режиме коэффициенты местного сопротивления ζ не зависят от числа Рейнольдса. Их значения , например, составляют:

Здесь т − коэффициент местного сопротивления при турбулентном режиме; В − коэффициент, определяемый для каждого вида местного сопротивления по справочникам.

Как правило, коэффициенты местных сопротивлений определяют экспериментально. Однако, есть и исключения, одно из которых рассматривается ниже.

5.2.1.Теорема Борда

Теорема позволяет определить коэффициент местного сопротивления для внезапного расширения трубы теоретическим путем. Для этого применяется е теорема о количестве движения: изменение количества движения тела mV за время t равно импульсу результирующей силы, действующей на тело P t . Характер движения предполагается установившимся и одномерным.

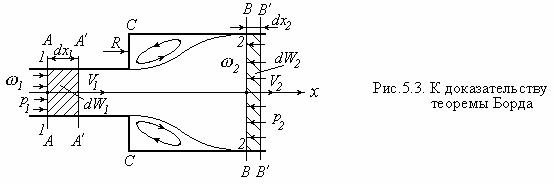
Поток жидкости, переходя от сечения ω1 к сечению ω2 , расширяется; при этом образуется вихревая зона, создающая значительные гидравлические потери (рис. 5.3). Опыты показывают, что справа у стенки С−С давление жидкости такое же, как сечении ω1 при выходе потока в расширенную область.

Применим теорему о количестве движения для объема жидкости, расположенного между сечениями А−А и В−В.

Сечение А−А выберем на малом расстоянии от расширения (чтобы можно было пренебречь путевыми потерями); сечение В−В − на участке широкой трубы, где поток уже подошел к боковым стенкам.

За время dt сечение A A переместится в положение A A , сечение B B переместится в положение B B . Объем, расположенный между сечениями A A и B B , входит как в начальное, так и в конечное положение выделенного объема. Поэтому можно полагать, что заштрихованный объем dW1 перешел в положение dW2.

Масса dm1объема dW1 равна dW1 1dx1 1V1dt . Масса dm2объема dW2 равна dW2 2dx2 2V2dt.

Так как при установившемся движении 1V1 2V2, то dm1 dm2 dm. Изменение количества движения массы dm равно dm(V2 V1). Результирующая сила P , действующая на выделенный объем, равна

P p1 1 R p2 2 .

Здесь R − реакция стенки С−С на объем справа от стенки. Эта реакция равна по величине силе давления жидкости на стенку, но направлена в противоположную сторону − от стенки к жидкости. Так как давление у стенки постоянно и равно р1, то R p1 2 1 p1 2 p1 1.

Таким образом, результирующая сила равна

P p1 1 p1 2 p1 1 p2 2 p1 p2 2.

Введем подстановку dm 2V2dt. Получим

2V2dt V2 V1 p1 p2 2dt .

Сократим на d 2 и dt.

V2 V2 V1 p1 p2.

Откроем скобки и разделим правую и левую части этой формулы на g .

В уравнении (5.5) первое слагаемое в левой части разобьем на две половины; второе слагаемое умножим и разделим на 2; в левой части, кроме того,

прибавим и вычтем V12 /2g . Получим:

В левой части сумму второго, третьего и четвертого членов представим как квадрат разности:

V22 V1 V2 2 V12 p1 p2 .

Перегруппируем слагаемые, перенеся члены с индексами «1» в левую часть: