
№3
1. Функция одной переменной. Определение предела функции в точке по Коши.Число bназывается пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любого положительного числа e существует такое положительное число d, что при всех х ≠ а, таких, что |x – a | < d, выполняется неравенство | f(x) – a | < e .
Определение предела функции в точке по Гейне. Число b называется пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любой последовательности {xn}, сходящейся ка (стремящейся к а, имеющей пределом число а), причем ни при каком значении n хn ≠ а, последовательность {yn = f(xn)} сходится к b.
Данные определения предполагают, что функция у = f(x) определена в некоторой окрестноститочки а, кроме, быть может, самой точки а.
Определения предела функции в точке по Коши и по Гейне эквивалентны: если число b служит пределом по одному из них, то это верно и по второму.
Указанный предел обозначается так:
![]()
Геометрически существование предела функции в точке по Коши означает, что для любого числа e > 0 можно указать на координатной плоскости такой прямоугольник с основанием 2d > 0, высотой 2e и центром в точке (а; b), что все точки графика данной функции на интервале (а–d; а + d), за исключением, быть может, точки М(а; f(а)), лежат в этом прямоугольнике – см. рис.:

Читать дальше...
Критерий Коши существования предела функции в точке. Число b – предел функции у = f(x) при х, стремящемся к а, тогда и только тогда, когда для любого числа e > 0 можно указать такую проколотую d-окрестность точки а, что для любых чисел х1 и х2, содержащихся в этой окрестности, выполняется неравенство | f(x1) – f(x2) | < e.
Пусть ![]()
![]() Тогда
существуют пределы суммы и произведения
функцийf(x)
и g(x),
а в случае с ≠ 0 – и частного этих функций,
причём:
Тогда
существуют пределы суммы и произведения
функцийf(x)
и g(x),
а в случае с ≠ 0 – и частного этих функций,
причём:
![]()
![]()
 Если
определенасложная
функция F(f(x)),
причём
Если
определенасложная
функция F(f(x)),
причём ![]()
![]() то
существует и предел сложной функции,
причём
то
существует и предел сложной функции,
причём
![]()
В теории пределов доказываются следующие два утверждения.
Первый
замечательный предел: ![]()
Второй
замечательный предел: ![]() гдее –
знаменитое иррациональное число, e=
2,71...
гдее –
знаменитое иррациональное число, e=
2,71...
При вычислении пределов для раскрытия неопределённостей, связанных с дифференцируемыми функциями, часто используют правило Лопиталя.
Читать далее...
2. Функция многих переменных. Пусть функция у = f(x1; x2; …; xn) определена в некоторой выколотой окрестности точки Р(р1; р2; …; рn), принадлежащей области n–мерного пространства, состоящей из точек Х(x1; x2; …; xn). Число b называется пределом функции у =f(x1; x2; …; xn) при Х, стремящейся к Р, если для любого числа e > 0 существует такое положительное число d, что в точках Х выколотой окрестности точки Р, задаваемой неравенствами

выполняется неравенство | f(x1;x2; ...;xn) – b | < e.
Односторо́нний преде́лвматематическом анализе—предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственнолевосторо́нним преде́лом(илипреде́лом сле́ва) иправосторо́нним преде́лом(илипреде́лом спра́ва).
Определение
Пусть
задана числовая
функция![]() и
и![]() —предельная
точкаобласти
определенияM.
—предельная
точкаобласти
определенияM.
Число ![]() называется
правосторонним пределом
функцииfприxстремящемся
кa,если
называется
правосторонним пределом
функцииfприxстремящемся
кa,если
![]()
Число ![]() называется
левосторонним пределом
функцииfприxстремящемся
кa,если
называется
левосторонним пределом
функцииfприxстремящемся
кa,если
![]()
Обозначения
Правосторонний предел принято обозначать любым из нижеследующих способов:
![]()
Аналогичным образом для левосторонних пределов приняты обозначения:
![]()
Односторонний предел как предел вдоль фильтра
Односторонний
предел является частным случаем общего
понятия предела
функции вдоль фильтра.
Пусть![]() и
и![]() Тогда
системы множеств
Тогда
системы множеств
![]()
и
![]()
являются фильтрами. Пределы вдоль этих фильтров совпадают с соответствующими односторонними пределами:
![]()
![]()
Свойства
Основные свойства односторонних пределов идентичны свойствам обычных пределови являются частными случаями свойств пределов вдоль фильтра.
Для существования (двустороннего) предела функции необходимо и достаточно, чтобы оба односторонних предела существовали и равнялись между собой.
Примеры
Функция из Примера 1.
Пусть ![]() и
и
![]()
Тогда (см. рис.)
![]()
![]() Поскольку
односторонние пределы функцииf(x)в
точке3различны,
то предела данной функции в0не
существует.
Поскольку
односторонние пределы функцииf(x)в
точке3различны,
то предела данной функции в0не
существует.
Пусть ![]() и
и![]() Тогда
Тогда
![]()
![]()
Опять, поскольку односторонние пределы функции f(x)в точке0различны, то предела данной функции в0не существует.
Предел функции на бесконечности. Пусть задана функция у = f(x) с неограниченной сверху областью определения. Число b называется пределом данной функции при х, стремящемся к плюс бесконечности, если для любого числа существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x > M, выполняется неравенство |f(x) – b| < e. Запись этого факта:
![]()
Если область определения данной функции неограниченна снизу, то число bназывается пределом данной функции при х, стремящемся к минус бесконечности, если для любого числа e < 0 существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x < –M, выполняется неравенство |f(x) – b| < e. Записывается это так:
![]()
7.5. Основные теоремы о пределах
Рассмотрим
теоремы о правилах предельного перехода.
Т.1: Предел постоянной равен самой
постоянной Доказательство следует из
определения предела функции, так как![]() если
с = const.
если
с = const.
Т.2:
(о связи функции с ее пределом). Для того
чтобы ![]() необходимо
и достаточно выполнение равенства
необходимо
и достаточно выполнение равенства![]() где
где![]() —
б.м. при х
—
б.м. при х![]() а
а![]()
![]()
![]()
—
б.м., х![]() а)
а)
Запишем цепочку равносильных утверждений, следующих из определения предела функции и определения б.м.:

Т.3:
Предел суммы конечного числа функций,
имеющих пределы при х![]() а,
равен сумме их пределов
а,
равен сумме их пределов
Пусть![]() тогда
по теореме 2 име-
тогда
по теореме 2 име-
ем![]() где
где![]() —
б.м. при
—
б.м. при
х![]() а,
следовательно,
а,
следовательно,![]() Используя
лемму 1 о б.м., заключаем, что
Используя
лемму 1 о б.м., заключаем, что![]() —
б.м. при
—
б.м. при
![]() и
по теореме 2 получаем равенство
и
по теореме 2 получаем равенство![]() b1
+ b2
b1
+ b2
Т.4:
Предел произведения конечного числа
функций, имеющих пределы при х![]() а,
равен произведению пределов Методика
доказательства аналогична доказательству
Т.3. Следствие. Постоянный множитель
можно выносить за знак предела.
а,
равен произведению пределов Методика
доказательства аналогична доказательству
Т.3. Следствие. Постоянный множитель
можно выносить за знак предела.
Т.5:
Предел отношения двух функций, имеющих
пределы при х![]() а,
равен отношению их пределов (если предел
знаменателя не нуль), т.е.
а,
равен отношению их пределов (если предел
знаменателя не нуль), т.е.
![]()
Пусть![]() тогда,
используя Т.2, аналогично доказательству
Т.3 запишем
тогда,
используя Т.2, аналогично доказательству
Т.3 запишем
![]()
где![]() Числитель
последней дроби по леммам о б.м. является
б.м. Покажем, что
Числитель
последней дроби по леммам о б.м. является
б.м. Покажем, что![]() является
функцией ограниченной, тогда дробь по
лемме 2 о б.м. является б.м., и по Т.2:
является
функцией ограниченной, тогда дробь по
лемме 2 о б.м. является б.м., и по Т.2:![]()
Имеем
в некоторой![]() окрестности
т. а для любого
окрестности
т. а для любого![]() >
0 вследствие справедливости
>
0 вследствие справедливости![]()
![]()
т.е.
ограниченность![]() доказана
доказана
№4
БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ СВОЙСТВА
Функция y=f(x) называется бесконечно
малой при x→a или
при x→∞,
если ![]() или
или![]() ,
т.е. бесконечно малая функция – это
функция, предел которой в данной точке
равен нулю.
,
т.е. бесконечно малая функция – это
функция, предел которой в данной точке
равен нулю.
Примеры.
Функция f(x)=(x-1)2 является бесконечно малой при x→1, так как
 (см.
рис.).
(см.
рис.).Функция f(x) = tgx – бесконечно малая при x→0.
f(x) = ln (1+x)– бесконечно малая при x→0.
f(x) = 1/x– бесконечно малая при x→∞.
Установим следующее важное соотношение:
Теорема. Если
функция y=f(x) представима
при x→aв
виде суммы постоянного числа b и
бесконечно малой величины α(x):
f (x)=b+ α(x) то ![]() .
.
Обратно,
если ![]() ,
тоf
(x)=b+α(x),
где a(x) –
бесконечно малая при x→a.
,
тоf
(x)=b+α(x),
где a(x) –
бесконечно малая при x→a.
Доказательство.
Докажем первую часть утверждения. Из равенства f(x)=b+α(x) следует |f(x) – b|=| α|. Но так как a(x) – бесконечно малая, то при произвольном ε найдется δ – окрестность точки a,при всех x из которой, значения a(x) удовлетворяют соотношению |α(x)|<ε. Тогда |f(x) – b|< ε. А это и значит, что
 .
.Если
 ,
то при любом ε>0 для
всех х из
некоторой δ – окрестность точки a будет |f(x)
– b|< ε.
Но если обозначимf(x)
– b= α,
то |α(x)|<ε,
а это значит, что a –
бесконечно малая.
,
то при любом ε>0 для
всех х из
некоторой δ – окрестность точки a будет |f(x)
– b|< ε.
Но если обозначимf(x)
– b= α,
то |α(x)|<ε,
а это значит, что a –
бесконечно малая.
Рассмотрим основные свойства бесконечно малых функций.
Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.
Доказательство.
Приведем доказательство для двух
слагаемых. Пусть f(x)=α(x)+β(x),
где ![]() и
и![]() .
Нам нужно доказать, что при произвольном
как угодно малом ε>0
найдетсяδ>0,
такое, что для x,
удовлетворяющих неравенству |x
– a|<δ,
выполняется |f(x)|< ε.
.
Нам нужно доказать, что при произвольном
как угодно малом ε>0
найдетсяδ>0,
такое, что для x,
удовлетворяющих неравенству |x
– a|<δ,
выполняется |f(x)|< ε.
Итак, зафиксируем произвольное число ε>0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ1>0, что при |x – a|<δ1 имеем |α(x)|< ε/2. Аналогично, так как β(x) – бесконечно малая, то найдется такое δ2>0, что при |x – a|<δ2 имеем | β(x)|< ε/2.
Возьмем δ=min{ δ1, δ2}.Тогда в окрестности точки a радиуса δбудет выполняться каждое из неравенств |α(x)|< ε/2 и | β(x)|< ε/2. Следовательно, в этой окрестности будет
|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)| < ε/2 + ε/2= ε,
т.е. |f(x)|<ε, что и требовалось доказать.
Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.
Доказательство. Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε>0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|< ε/M. Тогда в меньшей из этих окрестностей имеем | αf|< ε/M= ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично.
Из доказанной теоремы вытекают:
Следствие
1. Если ![]() и
и![]() ,
то
,
то![]() .
.
Следствие
2. Если ![]() иc=const,
то
иc=const,
то ![]() .
.
Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.
Доказательство.
Пусть ![]() .
Тогда 1/f(x) есть
ограниченная функция. Поэтому дробь
.
Тогда 1/f(x) есть
ограниченная функция. Поэтому дробь ![]() есть
произведение бесконечно малой функции
на функцию ограниченную, т.е. функция
бесконечно малая.
есть
произведение бесконечно малой функции
на функцию ограниченную, т.е. функция
бесконечно малая.
СООТНОШЕНИЕ МЕЖДУ БЕСКОНЕЧНО МАЛЫМИ
И БЕСКОНЕЧНО БОЛЬШИМИ ФУНКЦИЯМИ
Теорема 1. Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a.
Доказательство. Возьмем
произвольное число ε>0 и
покажем, что при некотором δ>0 (зависящим
от ε) при всех x,
для которых |x
– a|<δ,
выполняется неравенство ![]() ,
а это и будет означать, что1/f(x) –
бесконечно малая функция. Действительно,
так как f(x) –
бесконечно большая функция при x→a,
то найдется δ>0 такое,
что как только |x
– a|<δ,
так |f(x)|>1/ ε.
Но тогда для тех же x
,
а это и будет означать, что1/f(x) –
бесконечно малая функция. Действительно,
так как f(x) –
бесконечно большая функция при x→a,
то найдется δ>0 такое,
что как только |x
– a|<δ,
так |f(x)|>1/ ε.
Но тогда для тех же x![]() .
.
Примеры.
Ясно, что при x→+∞ функция y=x2+1 является бесконечно большой. Но тогда согласно сформулированной выше теореме функция
 –
бесконечно малая приx→+∞,
т.е.
–
бесконечно малая приx→+∞,
т.е.  .
. .
.
Можно доказать и обратную теорему.
Теорема 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y=1/f(x) является бесконечно большой функцией.
Доказательство теоремы проведите самостоятельно.
Примеры.
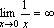 .
. .
. ,
так как функции
,
так как функции  и
и -
бесконечно малые приx→+∞,
то
-
бесконечно малые приx→+∞,
то  ,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же
,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A≠ 0
![]() .
.
