математика 1
.doc1. ФУНКЦИИ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ
Основные сведения из теории.
Пусть
произвольное множество действительных
чисел. Если каждому числу
поставлено в соответствие некоторое
вполне определенное число
,
то говорят, что на множестве
задана функция
или
.
При этом число
называется аргументом
или независимой
переменной,
а
- частным
значением функции
в точке
.
Пусть
-
совокупность всех частных значений для
.
Множество X называется областью
определения функции
(областью допустимых значений).
Множество Y называется областью значений функции.
Функция
называется
возрастающей
на интервале
,
если из неравенства
следует неравенство
.
Иными словами,
функция
называется
возрастающей
на интервале
,
если большему значению аргумента на
этом интервале соответствует большее
значение функции.
Функция
называется
убывающей
на интервале
,
если из неравенства
следует неравенство
.
Пример 1.
Покажем, что функция
для
монотонно убывающая. Так как
,
то, очевидно, большему возможному
значению
соответствует меньшее значение функции,
т.е. функция монотонно убывает для
.
Функция
называется ограниченной,
если существуют такие числа
и
,
что
для всех возможных значений аргумента
.
В противном случае
функция
называется неограниченной.
Пример 2. Функция
ограниченная, так как имеет место
очевидное неравенство
.
Функция
называется четной
(нечетной),
если
.
Замечание 1. Очевидно, область определения и четной и нечетной функции симметрична относительно начала координат.
Замечание 2.
График чётной функции симметричен
относительно оси
(рис. 1.5), a график нечётной функции
симметричен относительно начала
координат (рис. 1.6).
Справедливы следующие утверждения:
а) сумма двух нечетных функций есть нечетная функция;
б) сумма двух четных функций есть четная функция;
в) произведение двух четных или нечетных функций есть четная функция;
г) произведение четной и нечетной функций есть нечетная функция.
Пример 3.
Докажем, что функция
четная.
Функция
четная (произведение двух нечетных
функций), выражение
четное (сумма и разность четных функций).
Пример 4.
Функция
является функцией общего вида (ни четная,
ни нечетная), так как область определения
этой функции не симметрична относительно
начала координат.
Функция
называется периодической,
если существует такое отличное от нуля
число
,
что для любого
из области определения функции имеет
место равенство
.
Наименьшее из таких чисел называется периодом функции.
Если функция
может быть однозначно представлена в
виде
,
то говорят, что для функции
существует обратная функция. (Графики
функций
и
совпадают.)
Если в функции
поменять местами
и
,
то получим функцию
,
которая называется обратной
к функции
.
(Графики функций
и
симметричны относительно прямой
.)
Пример 5.
Функция
может быть представлена в виде
(графики этих функций совпадают). Поменяем
местами
и
в последнем выражении. Получим функцию
,
которая является обратной к функции
.
(Графики функций
и
симметричны относительно прямой
.)
Прямая, к которой неограниченно приближаются точки кривой при их удалении в бесконечность, называется асимптотой этой кривой.
Элементарные функции и их графики.
Степенная функция.
Функция
,
где
и
,
называется степенной
функцией.
Рис. 1.1 Графики
функций а)
(сплошная
линия);
б)
(пунктирная линия).
Рис. 1.2 Графики
функций а)
(сплошная
линия);
б)
(пунктирная линия).
Рис. 1.3 Графики
функций а)
(сплошная
линия);
б)
(пунктирная линия).
Рис. 1.4 Графики
функций
(сплошная линия);
б)
(пунктирная линия).
1) Основные
характеристики и свойства степенной
функции
при
и
- чётное (рис. 1.1):
а)
область определения функции;
б)
область значений функции;
в) функция монотонно
убывающая для отрицательных значений
и монотонно возрастающая для положительных;
г) функция чётная.
2) Основные
характеристики и свойства степенной
функции
при
и
- нечётное (рис. 1.2):
а)
область определения функции;
б)
область значений функции;
в) функция монотонно возрастающая;
г) функция нечётная.
3) Основные
характеристики и свойства степенной
функции
при
и
- чётное (рис. 1.3):
а)
область определения функции;
б)
область значений функции;
в) функция монотонно
возрастающая для отрицательных значений
и монотонно убывающая для положительных;
г) функция чётная.
4) Основные
характеристики и свойства степенной
функции
при
и
- нечётное (рис. 1.4):
а)
область определения функции;
б)
область значений функции;
в) функция монотонно
убывающая для всех
,
принадлежащих области определения
функции;
г) функция нечётная.
Обратите внимание! На рис. 1.1-1.4 изображены и графики степенных функций с дробными показателями:
а)
(ОДЗ:
),
обратная к
,
где
;
б)
(ОДЗ:
),
обратная к
;
в)
(ОДЗ:
),
обратная к
где
;
г)
(ОДЗ:
),
обратная к
.
Показательная функция.
Логарифмическая функция.
Функция
,
где
,
и
называется показательной
функцией.
Основные характеристики и свойства показательной функции (рис. 1.5-1.6):
а)
область определения функции
;
б)
область значений функции
;
в) функция
монотонна
(возрастает при
и убывает при
).
Рис. 1.5 Графики
функций: а)
(пунктирная линия);
б)
(сплошная линия).
Рис. 1.6 Графики
функций
и
.
Функция
,
где
,
и
,
называется логарифмической
функцией.
Эта функция является обратной к показательной функции (см. рис. 1.5-1.6).
Основные характеристики и свойства логарифмической функции:
а)
- область определения функции
;
б)
-
область значений функции
;
в) функция
монотонна (возрастает при
и убывает при
);
г) функция
неограниченная, непрерывная,
непериодическая;
д)
(т.е. график функции
проходит через точки
).
Тригонометрические функции.
К тригонометрическим функциям относятся
,
,
и
.
Функция
называется синусоидой.
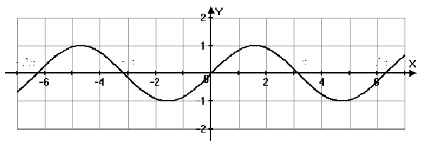
Рис. 1.7 Графики
функции
.
Основные
характеристики и свойства функции
:
а)
- область определения функции
;
б)
-
область значений функции
;
в) функция
периодическая (период равен
);
г) функция
непрерывная, ограниченная
;
д)
где
целое число (т.е. график функции
проходит через точки
).
График функции
может быть
получен сдвигом графика функции
вдоль оси
на
.
Рис.1.8 Графики
функции
.
Основные
характеристики и свойства функции
:
а)
- область определения функции
;
б)
-
область значений функции
;
в) функция
периодическая (период равен
);
г) функция
непрерывная, неограниченная;
д)
где
целое число (т.е. график функции
проходит через точки
).
е)
- вертикальные асимптоты графика функции
.
Рис. 1.9 График
функции
.
.
Рис. 1.10 График
функции
.
Обратные тригонометрические функции.
К обратным
тригонометрическим функциям относятся
,
,
и
.
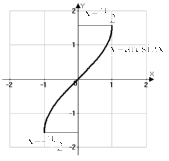
Рис. 1.11 Графики
функций
и
.
Основные
характеристики и свойства функции
:
а)
- область определения функции
;
б)
-
область значений функции
;
в) функция
монотонно возрастающая функция;
г) функция
непрерывная, ограниченная
;
д)
(т.е. график функции
проходит через начало координат).
Рис. 1.12 График
функции
.
Рис. 1.13 График
функции
.
Основные
характеристики и свойства функции
:
а)
- область определения функции
;
б)
-
область значений функции
;
в) функция
монотонно возрастающая функция;
г) функция
непрерывная, ограниченная
;
д)
(т.е. график функции
проходит через начало координат).
Задачи для самостоятельной работы (задание №1).
1.16.
.
Найти
,
,
,
,
,
.
1.17.
Пусть
.
а) Показать, что
функция
чётная, если функция
определена на интервале
;
б) Найти
если
.
1.18.
Найти приращение функции
,
если
.
1.19.
Найти все значения
и
,
при которых справедливо тождество
,
если
.
1.20. Пусть
а) Указать область определения этой функции.
б) Построить график
функции
.
в) Найти
г) Решить графически
и аналитически уравнение
.
1.21. Найти область определения следующих функций:
а)
б)
в)
г)
д)
е)
ж)
з)
1.22. Установить, какие из следующих функций являются четными и какие нечетными:
а)
б)
в)
г)
1.23.
Пусть
Найти
