8. Оценка качества регулирования

Качество любой системы регулирования в большой степени определяется величиной ошибки регулирования, равной разности между управляющим воздействием и регулируемой величиной Знание мгновенных значений ошибки в течении всего времени работы объекта позволяет наиболее полно судить о свойствах системы регулирования. Однако на этапах проектирования таких знаний недостаточно. Поэтому разработаны другие критерии, позволяющие оценивать показатели качества системы и более того обеспечивать необходимые свойства системе в процессе проектирования.

Все критерии и условно разделены на несколько групп:

К первой группе отнесены критерии, использующие для оценки качества величину статической ошибки в различных типовых режимах.

Ко второй группе относятся критерии, определяющие величину запаса устойчивости. Эти критерии позволяют почувствовать, как далеко от границы устойчивости находится система регулирования. Наиболее опасной для системы является колебательная граница устойчивости, когда пара комплексных корней характеристического уравнения попадает на мнимую ось комплексной плоскости. Это возникает в случае чрезмерного увеличения коэффициента усиления разомкнутой системы;

Третья группа критериев определяет быстродействие систем регулирования. Под быстродействием понимается время реагирования системы на появление внешних воздействий. Быстродействие обычно оценивается по времени затухания переходного процесса в системе. Существуют и др. группы критериев [1].

8.1. Статическая точность систем регулирования

Статическая точность определяется на установившемся режиме, который наступает при времени t → ∞. Ошибка регулирования в этом случае называется статической и состоит из двух составляющих:

(1.113)

где − часть статической ошибки, определяемая управляющим воздействиемg(t);

−часть статической ошибки, определяемая возмущающим воздействием f(t), рис.1.50.

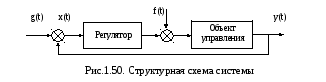
Выполним анализ зависимостей величин статических ошибок для различных режимов изменения управляющего воздействия g(t) при наличии и отсутствия возмущения f(t):

1. В качестве первого типового режима рассмотрим установившееся состояние при постоянных значениях управляющего и возмущающего воздействий.

Пусть управляющее воздействие g(t) = g₀, а возмущение f(t) = 0. Для расчета ошибки воспользуемся выражением для передаточной функции системы по ошибке

, (1.114)

где − передаточная функция разомкнутой системы.

Для установившегося состояния можно записать

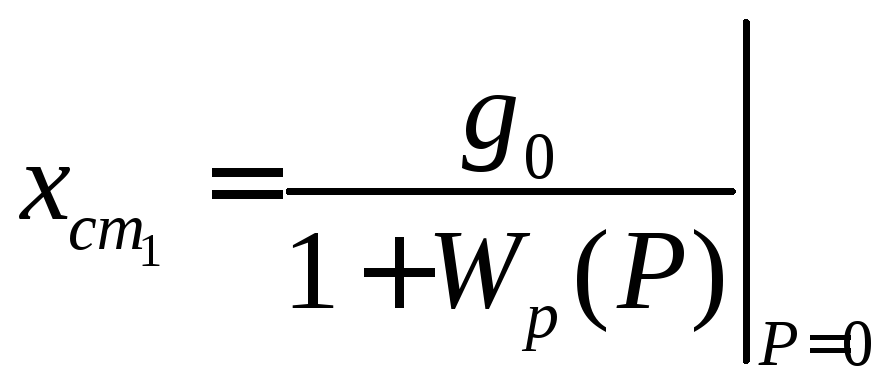. (1.115)

Рассмотрим пример. Пусть регулятор и объект управления являются позиционными звеньями и имеют следующие передаточные функции:

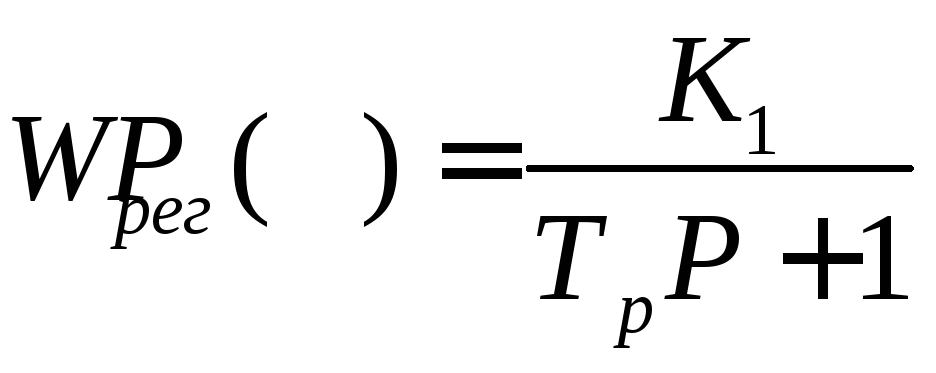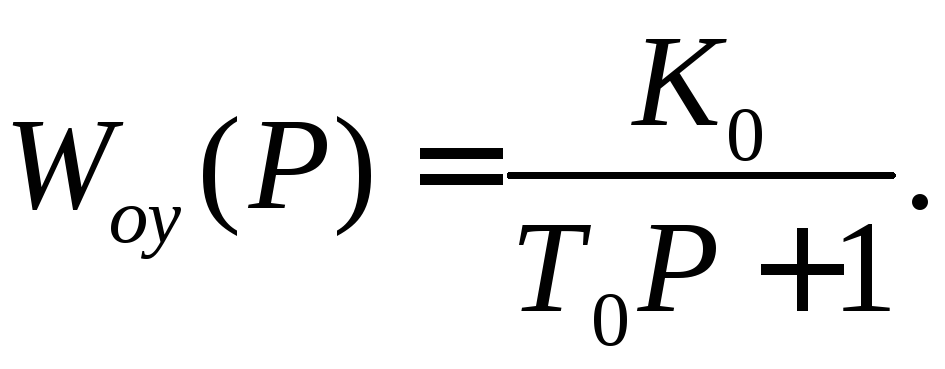, (1.116)

С учетом передаточных функций выражение (1.115) принимает вид

(1.117)

где − коэффициент передачи разомкнутой системы.

Из выражения (1.117) следует, что величина рассматриваемой ошибки зависит от коэффициента передачи. Для уменьшения ошибки необходимо увеличивать этот коэффициент. Однако необходимо помнить, что с увеличением коэффициентасистема приближается к границе устойчивости.

Если регулятор имеет передаточную функцию интегрирующего типа 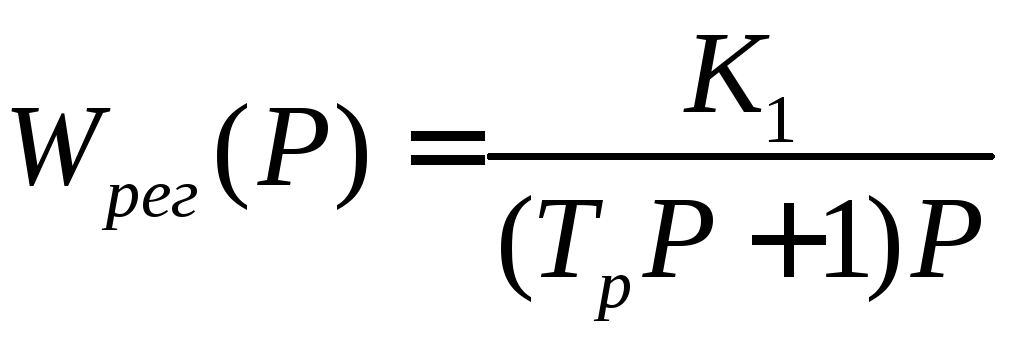, (1.118)

то выражение (1.115) примет вид

.

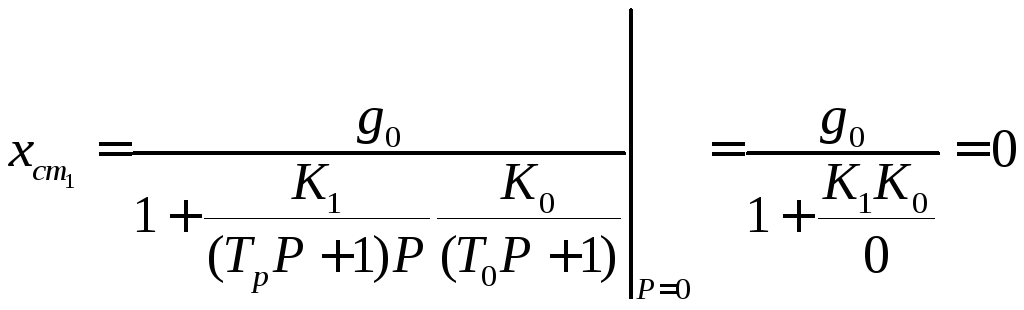Видно, что ошибка . Аналогичный результат получается и в случае, когда передаточная функция объекта управления представляется интегрирующим звеном.

Теперь рассмотрим случай, когда управляющее воздействие g(t) = 0, а возмущение f(t) = f₀.

Для расчета ошибки воспользуемся выражением для передаточной функции системы, определяющей связь между ошибкой регулирования и действующим возмущением

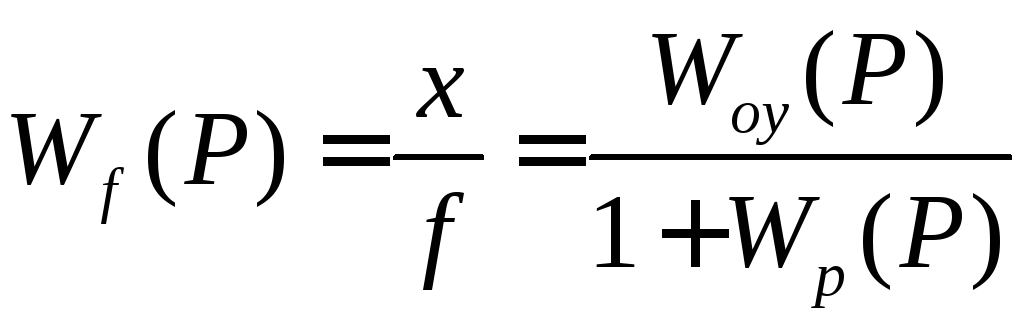. (1.119)

Для установившегося состояния можно записать

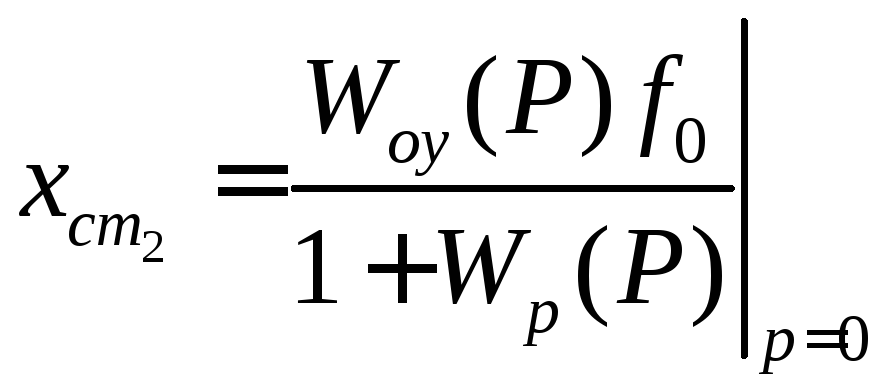(1.120)

Опять рассмотрим пример. Пусть регулятор и объект регулирования имеют передаточные функции, соответствующие выражениям (1.116). С учетом этого выражение (1.120) принимает вид

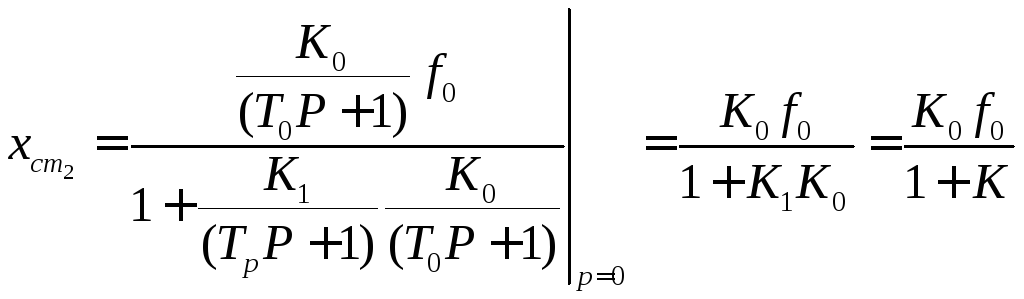. (1.121)

Видно, что статическая ошибка больше нуля. Величина ошибки, как и в ранее рассмотренном примере (1.116) зависит в основном от коэффициента передачи разомкнутой системы.

Если применить регулятор интегрирующего типа (1.118), то из выражения (1.121) нетрудно понять, что в этом случае статическая ошибка равна нулю.

Из рассмотренных примеров следует, что статическая ошибка характерна для систем регулирования, у которых регулятор в своем составе не имеет интегрирующих звеньев. Далее можно записать полное выражение для статической ошибки (1.113)

2. В качестве второго типового режима для САР рассмотрим изменение управляющего воздействия с постоянной скоростью

g(t) = v*t, (1.122)

где v − постоянный коэффициент.

Этот режим применяется только в следящих системах и в системах программного регулирования.

Примем, что возмущения в системе отсутствуют, т. е. .

С учетом (1.122) выражение для расчета ошибки (1.115) запишется в виде

.

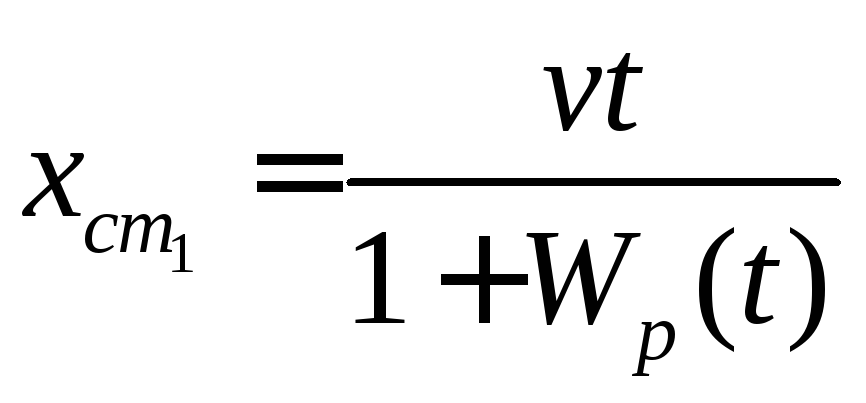Применяя изображение Карсона − Хевисайда [1] , можем записать окончательный вид выражения для расчета статической ошибки

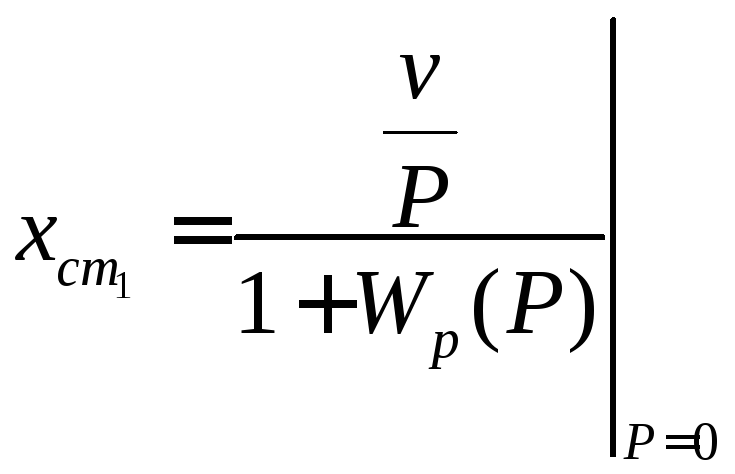
Рассмотрим пример. Пусть передаточные функции регулятора и объекта регулирования соответствуют выражениям (1.116). Тогда выражение для составляющей статической ошибки будет иметь вид

Видно, что составляющая ошибки стремится к бесконечности.

Если в качестве регулятора применить интегрирующее звено, то величина статической ошибки будет конечной:

,

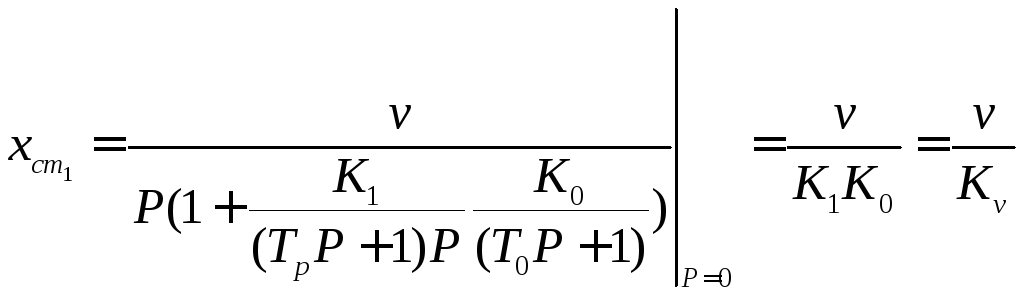где коэффициент называется добротностью системы по скорости.

Видно, что имеет место конечная величина ошибки, равная отношению заданной скорости к добротности системы. Данная ошибка называется скоростной. Системы регулирования, у которых регулятор и объект регулирования представлены позиционными звеньями, называют статическими. Если в качестве регулятора применяются интегрирующие звенья, то САР называют астатическими первого или второго порядка, в зависимости от количества интегрирующих звеньев в регуляторе.

Выполненный анализ показывает, что режим движения с постоянной скоростью не должен применяться к статическим системам, так как в установившемся состоянии величина статической ошибки стремится к бесконечности. Этот режим движения применим только к астатическим системам, которые имеют конечную величину статической ошибки, зависящей от добротности системы по скорости.

Случай, когда , аранее рассматривался. Было показано, что, если регулятор системы содержит интегрирующее звено, то составляющая статической ошибки. Следовательно, в рассматриваемых астатических САР эта составляющая не формирует статическую ошибку.

3. Третьим типовым режимом, применяемым в САР, является движение по гармоническому закону:

g(t) = g^max sin(ω_kt),

где g^max − максимальная величина управляющего воздействия g(t),

ω_к − частота гармонического закона.

В данном анализе возмущающие воздействия могут отсутствовать или иметь постоянные значения. Случай постоянства возмущений приводит, как и в рассмотренных выше первом и втором типовых режимах, к появлению некоторой постоянной составляющей ошибки .

Запишем уже известное выражение для ошибки

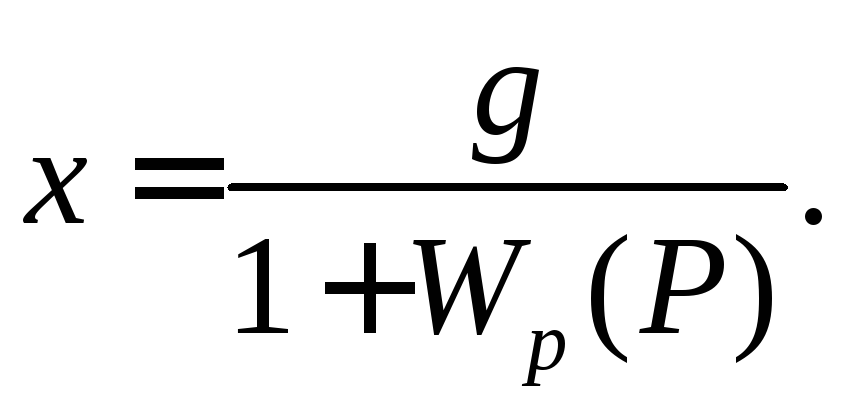
В линеаризованной системе при гармоническом управляющем воздействии ошибка в установившемся режиме будет также изменяться по гармоническому закону с частотой ω = ω_к , т.е.

=sin(ω_kt+ψ).

Поэтому точность САР в этом режиме оценивается по амплитуде ошибки, которая может быть найдена по выражению

.

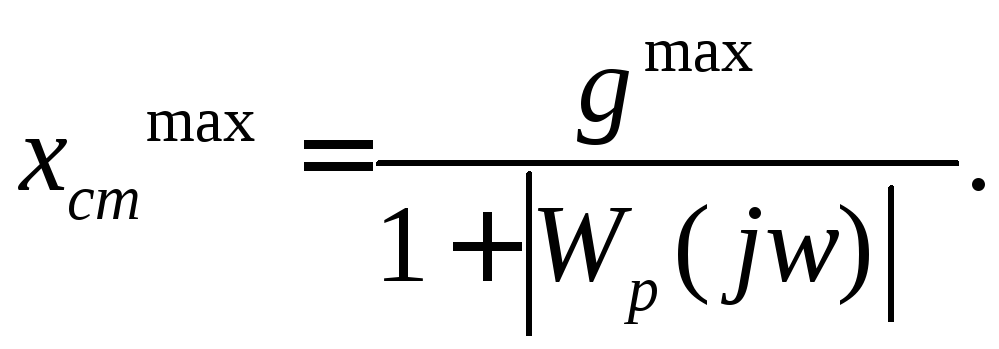Так как предполагается, что х^max << g^max, то >> 1. Следовательно, можно записать, что

(1.123)

где − модуль частотной передаточной функции разомкнутой системы при частоте ω = ω_k.

Формула (1.123) позволяет вычислить амплитуду ошибки в установившемся режиме. Для этого необходимо иметь либо аналитическое выражение для передаточной функции разомкнутой системы, либо экспериментальную амплитудно-частотную характеристику.

Выражение (1.123) позволяет сформулировать требования к АЧХ, которые необходимо выполнить при расчете систем регулирования для обеспечения заданной точности. Для этого по заданному значению амплитуды управляющего воздействия g^max и допустимой амплитуде ошибки вычисляется требуемое значение А_к=. Далее необходимо величину А_к отложить на графике АЧХ при частоте ω = ω_к. Полученная точка А_к называется контрольной точкой. Для того, чтобы амплитуда ошибки в системе не превосходила допустимого значения линия АЧХ должна проходить не ниже контрольной точки А_к.

8.2. Оценка запаса устойчивости и быстродействия САР

Оценку запаса устойчивости и быстродействия САР можно выполнить по виду кривой переходного процесса (рис.1.51), возникшего в результате приложения к системе типового внешнего воздействия.

В качестве такого воздействия обычно рассматривается единичный скачок. В этом случае кривую переходного процесса называют переходной характеристикой системы.

Переходная характеристика может строиться для регулируемой величины или для ошибки регулирования.

Склонность системы к колебаниям и запас устойчивости могут быть охарактеризованы величиной перерегулирования

σ % = [y_max− y(∞)] / y(∞)*100% ,

где у(∞) − установившееся значение регулируемой величины, после завершения переходного процесса.

Считается, что запас устойчивости достаточен, если величина перерегулирования не превышает 10  30 %. Быстродействие системы может определяться по длительности переходного процесса .

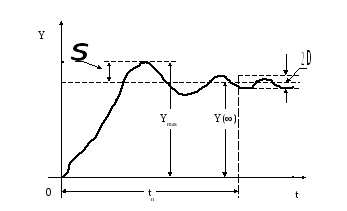
Рис.1.51. Кривая переходного процесса

Длительность переходного процесса определяется как время, протекающее от момента приложения на вход единичного скачка до момента, после которого имеет место неравенство

| y(t) − y(∞)|  ∆,

где ∆ − заданная малая постоянная величина, представляющая собой допустимую ошибку, ∆ ( .01 .05 ) у(∞) [2].

Иногда в дополнение к величине перерегулирования задается допустимое число колебаний, которое может наблюдаться в течение времени переходного процесса. Количество колебаний должно составлять 13.

Необходимый запас устойчивости, и быстродействие системы достигается в процессе расчета САР. Для расчета широко применяются частотные и корневые критерии и показатели качества регулирования.

Под частотными критериями понимают такие критерии, которые для оценки качества САР не опираются на формы переходных процессов, а используют для этого некоторые частотные свойства системы.

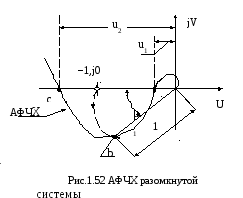
Частотные критерии наиболее разработаны для оценки запаса устойчивости. Запас устойчивости предлагается определять по удалению амплитудно-фазовой частотной характеристики разомкнутой системы (рис.1.52) от точки (− 1, 0). Для этого вводятся понятия запаса устойчивости по амплитуде (модулю) и запаса устойчивости по фазе.

Для общего случая условной устойчивости, изображенного на рис.1.52, запас устойчивости по амплитуде определяется расположением на вещественной оси комплексной плоскости точек и:

= 20 lg ;= 20 lg.

a

Запас устойчивости по амплитуде тем больше, чем больше и. В хорошо демпфированных системах величиныинаходятся в диапазоне 6 20 дб. В случае абсолютной устойчивости имеет смысл только величина .

Запас устойчивости по фазе (Рис.1.52) характеризует удаление АФЧХ по дуге окружности единичного радиуса от точки с координатами (−1,j,0) и соответствует углу μ между отрицательным направлением действительной оси и лучом, проведенным через начало координат и точку пересечения годографа характеристики с окружностью единичного радиуса. Величина запаса устойчивости по фазе определяется по выражению μ = 180˚ + ψ, где ψ − аргумент (смещение, сдвиг по фазе) частотной передаточной функции разомкнутой системы, соответствующий амплитуде равной единице (точкаb на рис.1.52).

В хорошо демпфированных системах запас по фазе составляет 3060˚.

Недостатком рассмотренного частотного критерия является то, что для определения запаса устойчивости необходимо задавать два числа: μ и .

Более удобно запас устойчивости определять по показателю колебательности. Показателем колебательности называется максимальное значение ординаты М^мах амплитудно - частотной характеристики замкнутой системы (рис.1.53) при начальной ординате, равной единице, т. е. относительная высота резонансного пика.

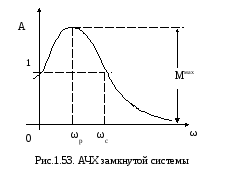
Чем меньше запас устойчивости, тем больше склонность системы к колебаниям и тем выше резонансный пик. Допустимое значение для показателя колебательности определяется на основании опыта эксплуатации систем регулирования. Считается, что в хорошо демпфированных системах регулирования показатель колебательности не должен быть больше 1.11.5. Однако, в отдельных случаях допускается величина М^мах =22.5 [2].

Корневые критерии качества опираются на существующую связь характера и качества переходных процессов в системе автоматического регулирования от расположения корней характеристического уравнения на комплексной плоскости. Поэтому можно сформулировать требования по запасу устойчивости и быстродействию системы посредством наложения условий на расположение корней характеристического уравнения. Заметим, что влиять на расположение корней можно только через коэффициенты характеристического уравнения:

(1.124)

Решение данного уравнения содержит - корней:Уже известно, что корни могут быть вещественными и комплексными типа= − α j. Колебания в системе будут наблюдаться, если в решении характеристического уравнения будет присутствовать хотя бы один комплексный корень. Склонность системы к колебаниям может характеризоваться отношением мнимой части корня к его вещественной части Это отношение называют колебательностью

μ=. (1.125)

Если в решении характеристического уравнения присутствует несколько комплексных корней, то для определения колебательности системы необходимо брать отношение (1.125) для тех корней, для которых это отношение наибольшее.

Колебательность системы связана с другим корневым показателем запаса устойчивости − затуханием. Рассмотрим эту связь. Комплексные сопряженные корни дают в выражении для переходного процесса, например для ошибки регулирования, член вида

x(t) = Ce ^{– αt} sin (t+ψ).

Н

айдем затухание амплитуды синусоидального колебания за один период. При некотором времениt = t₁ эта амплитуда равна С₁ = Сe ^–αt_. Через один период Т = 2π/ амплитуда С₂ = Сe ^{– α (t}₁^{+ 2π /)} = C₁e ^{- 2π α/} = C₁e ^{-2π /μ}.

Затуханием за период называют величину

 =

Эта величина обычно выражается в процентах. Поставляя значение амплитуды С₂, получаем  =1 − e^−2π/μ или μ = 2π / ln [1/(1−)].

Обычно в системах автоматического регулирования допускается затухание за период не менее чем 90  98 %. Так, например, если  = 98 %, то колебательность при этом составит

μ = 2π / ln 50 ≈ π/2 = 1.57.

Если  =90 %, то колебательность μ ≈ 2.72 [2].

Для оценки быстродействия системы может использоваться показатель, называемый степенью устойчивости. Под степенью устойчивости ή понимается абсолютное значение вещественной части ближайшего к мнимой оси корня (рис.1.54).

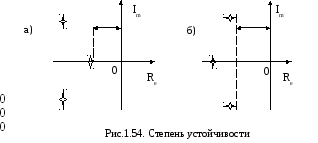
Корни характеристического уравнения, расположенные ближе к мнимой оси дают в переходном процессе (1.102) составляющие, которые затухают наиболее медленно, так как эти корни имеют наименьшую по абсолютной величине вещественную часть. В большинстве случаев переходный процесс можно считать завершенным после затухания составляющей, соответствующей ближайшему к мнимой оси корню. Если ближайшим является вещественный корень, то составляющая в переходном процессе, определяемая этим корнем будет иметь вид =C e ^–t. Приняв в конце переходного процесса =ΔC, где Δ = 0.01  0.05, можно получить приближенную зависимость между степенью устойчивостью и временем переходного процесса:

t_n ≈ ln Δ ⁻¹ . (1.126)

Так, например, если принять Δ = .05, то время переходного процесса t_n ≈ ln2 = 3. (1.127)

Если ближайшими к мнимой оси является пара комплексных корней , то составляющая в переходном процессе, определяемая этими корнями будет =sin(t + ψ). Несмотря на присутствие в этой составляющей гармонической функции формула, устанавливающая связь между степенью устойчивости и временем переходного процесса практически будет совпадать с выражением (1.127).

Для систем невысокого порядка степень устойчивости можно найти без вычисления корней характеристического уравнения. С этой целью в уравнении (1.124) необходимо перейти к новой переменной . Подставив в уравнение (1.124) , получим так называемое смещенное уравнение

Раскрывая скобки и группируя члены по степеням переменной , получаем

(1.128)

Это уравнение соответствует смещению осей на плоскости корней влево на величину (рис.1.54). В результате один (рис.1.54,а) или два (рис.1.54,б) корня попадают на ось мнимых, что соответствует границе устойчивости.

Для вычисления степени устойчивости необходимо применить к смещенному уравнению (1.128) любой критерий устойчивости и определить, при каком значении =получается граница устойчивости. Однако, если характеристическое уравнение имеет порядок выше второго, то задача расчета степени устойчивости оказывается не менее сложной, чем расчет корней характеристического уравнения. Например, если в уравнении (1.128) принять, то смещенное уравнение принимает вид:

(1.129)

где ,

²,

²³.

Видно, что для вычисления степени устойчивости (как и для вычисления корней исходного характеристического уравнения) необходимо решать алгебраическое уравнение третьей степени. Если характеристическое уравнение будет иметь пятый порядок, то для расчета степени устойчивости необходимо будет решать алгебраическое уравнение пятого порядка и т.д. В связи со сложностью решения алгебраических уравнений применение формулы (1.127) для расчета времени переходного процесса оказывается проблематичным.

Однако, применение степени устойчивости оказывается перспективным в задаче обеспечения требуемого быстродействия, возникающей при проектирования системы.

Пусть смещенное уравнение (1.128) относится к проектируемой системе. Этап проектирования соответствует расчету области устойчивости. Для придания системе требуемого быстродействия необходимо выполнить следующее:

задать требуемое время переходного процесса и по формуле (1.127) вычислить величину_.;

по формулам (1.129) с учетом рассчитать коэффициенты ;

изменяя переменные параметры, в плоскости которых строилась область устойчивости, необходимо переместить рабочую точку на границу устойчивости.

После выполнения указанных действий полученная система регулирования будет иметь время переходного процесса равное и соответствующие значения переменных параметров.

Диаграмма Вышнеградского (рис.1.55) позволяет существенно облегчить процесс проектирования систем управления. Несмотря на то, что диаграмма разработана для систем, имеющих характеристическое уравнение третьего порядка, ее применение может существенно облегчить расчет показателей качества и для систем более высокого порядка.

Рассмотрим характеристическое уравнение третьего порядка

(1.130)

Данное уравнение приводится к нормированному виду,

где

называются параметрами Вышнеградского, а − это новая переменная, введенная в уравнение (1.130), вместо переменной.

Диаграмма расположена в плоскости параметров А и В (рис.1.55) и содержит несколько основных кривых линий. Первая линия − граница устойчивости (колебательная). Уравнение границы: АВ = 1, при А > 0 и В > 0. Это равнобокая гипербола, для которой оси координат служат асимптотами.

В

6 4 2 0	2 область	3 область
			1область
Граница устойчивости

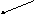
А

2 4 6

0

Рис. 1.55. Диаграмма Вышнеградского

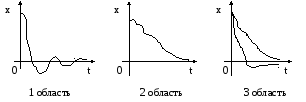
Рис. 1.56. Формы кривых переходных процессов

Область устойчивости находится выше этой кривой. Область устойчивости разбита на три части. На рисунке этим частям даны названия: 1-ая, 2-ая и 3-я области. В каждой области размещена схема расположения корней характеристического уравнения на комплексной плоскости, а на рис. 1.56 приведены типовые для областей формы переходных процессов. Точка С имеет координаты А=3 и В=3. Эта точка является общей для всех областей. Уравнения кривых, разделяющих область устойчивости, в данном материале не рассматриваются. При необходимости эти уравнения можно найти в известной литературе [1].

Диаграмма построена Вышнеградским в 1876 году в работе, которая положила начало развитию теории автоматического регулирования. На диаграмме показаны схемы расположения корней внутри каждой из трех частей области устойчивости. В области 3, где все корни вещественные, в зависимости от начальных условий получаются только апериодические переходные процессы. Формы таких процессов показаны на рис.1.56. Область 3 носит название области апериодических процессов. В областях 1 и 2, где имеется один вещественный корень и пара комплексных, переходные процессы будут иметь соответственно формы, показанные на первых двух графиках рис.1.56. В области 1 быстрее затухает экспонента, и поэтому переходный процесс будет определяться в основном колебательной составляющей. Это будет область колебательных процессов. В области 2, наоборот, быстрее затухает колебательная составляющая. Это будет область монотонных процессов. В последующие годы диаграмма получила дальнейшее развитие. Для более точного определения формы переходного процесса на плоскость диаграммы нанесены вспомогательные линии, разбивающие области 1, 2 и 3 на еще более мелкие части. Это линии равной степени устойчивости = соnst, линии равного затухания переходных процессов  = const и др. Подробнее об этих линиях в [1].

8.3.Учет начальных условий при расчете переходных процессов

Переходный процесс возникает в системе при подаче на ее вход внешнего воздействия. Дифференциальное уравнение обыкновенной линейной системы автоматического регулирования, записанное для регулируемой величины имеет вид:

(1.131)

,

где р = - алгебраический оператор дифференцирования,

g(t) – управляющее воздействие.

Уже отмечалось, что решение данного уравнения состоит из двух частей общегои частного, т.е.

(1.132) Общее решение представляет собой решение однородного уравнения

. (1.133) Это решение имеет вид

, (1.134)

где С₁, С₂ … С_n - произвольные постоянные, зависящие от начальных условий процесса, а корни характеристического уравнения (1.106).

Частное решение определяется правой частью уравнения (1.104) и соответствует установившемуся режиму, который наступает после затухания функции. Для нахождения полного решения можно записать

.

Далее требуется найти численные значения для постоянных и для корней. В большинстве случаев такие вычисления оказываются чрезмерно объемными и трудоемкими. Поэтому для получения кривых переходных процессов в настоящее время применяют численные методы решения дифференциальных уравнений и электронные вычислительные машины.

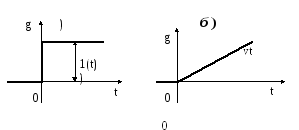
Для построения переходных процессов используют различные внешние воздействия. Наиболее распространенными являются типовые воздействия в виде единичной ступенчатой функции g(t) = 1(t) и в виде воздействия, изменяющегося по линейному закону g(t) = v*t ( рис.1.57,а и рис.1.57,б). Запишем уравнение (1.131) для случая, когда g(t) =1(t).

Рис.1.57. Типовые внешние воздействия

а) g(t) = 1(t) б)g=vt

Рис.1.45. Управляющие воздействия

Для численного решения необходимо это уравнение записать с правой частью, в которой оставить только коэффициент

·1(t). (1.135)

и систему начальных условий [2]:

·1(t),

·1(t) −,

·1(t) − − (1.136)

. . . . . . . . . . . . . . . . . . . . . . . . .

·1(t) − .

В системе (1.136) данные являются начальными значениями для производных и т.д. Введение начальных условий позволяет учесть влияние отсутствующих в правой части уравнения (1.135) коэффициентов

Рассмотрим пример. Пусть уравнение системы имеет , (1.137)

где .

Очевидно, что Для интегрирования уравнение (1.137) запишем в виде (1.135)

. (1.138)

Введем обозначение и запишем (1.138) в форме Коши

= . (1.139)

Далее по формулам (1.136) необходимо определить начальные условия :

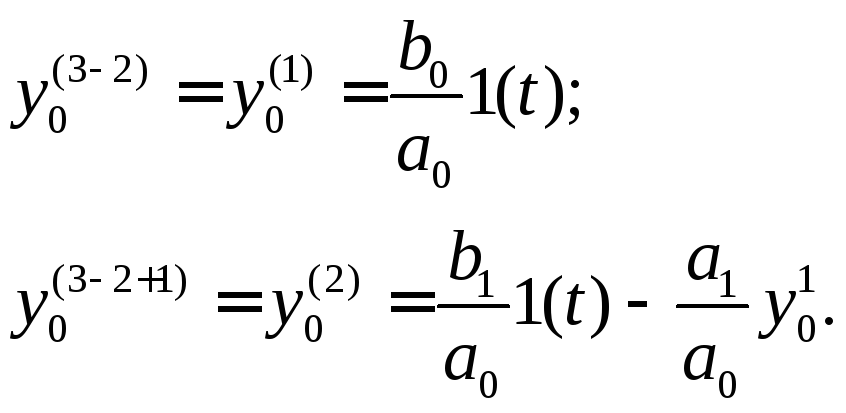(1.140)

В формулах (1.140) иобозначают начальные данные для производныхив системе уравнений (1.139). С учетом численных значений коэффициентов уравнения (1.137):5 и.

На рис.1.58 показаны переходные процессы, соответствующие приведенным выше численным значениям коэффициентов и начальным условиям.

Видно, что с течением времени значения производных истремятся к нулю, а значение переменнойк величине отношения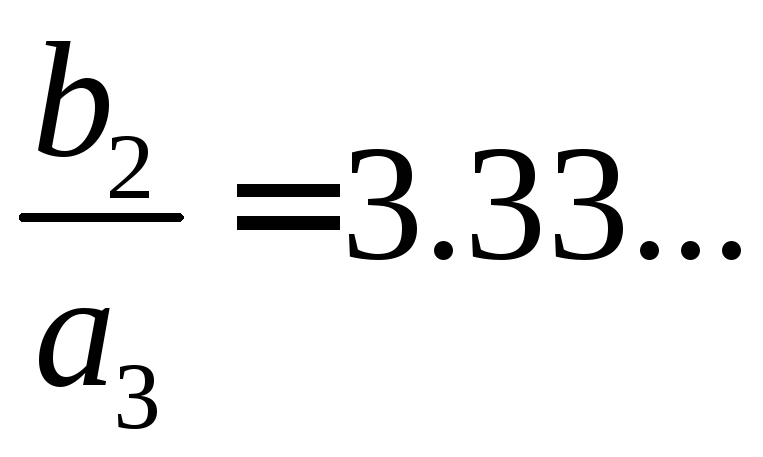

Теперь получим переходный процесс для случая, когда управляющее воздействие изменяется по линейному закону g (t) = vt, рис.1.52,б. Такой закон применяется в следящих системах и в системах программного регулирования.

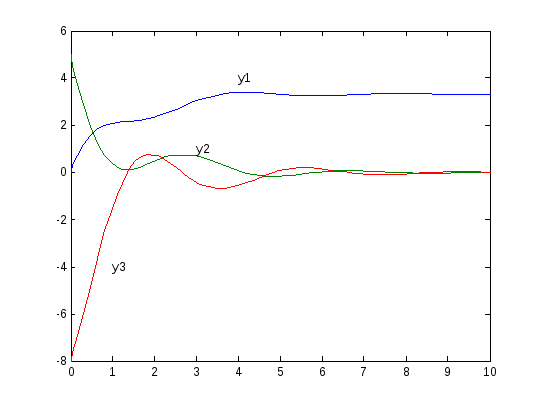
Рис.1.58. Переходные процессы

. В этом случае уравнение (1.111) следует записать в виде

(1.141)

где v − постоянный коэффициент (скорость изменения управляющего воздействия), t − время.

Используя изображения Карсона-Хевисайда , уравнение (1.141) можно записать в виде

(1.142)

Как и в предыдущем случае, уравнение (1.142) необходимо записать в форме Коши. Также вводится обозначение и записывается система уравнений:

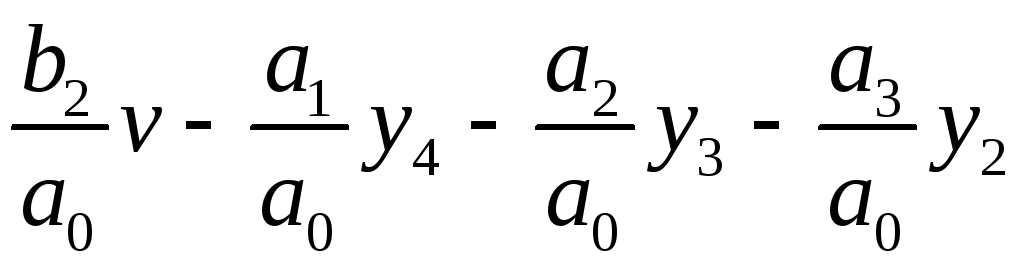= . (1.143)

Далее по формулам (1.136) необходимо рассчитать начальные условия:

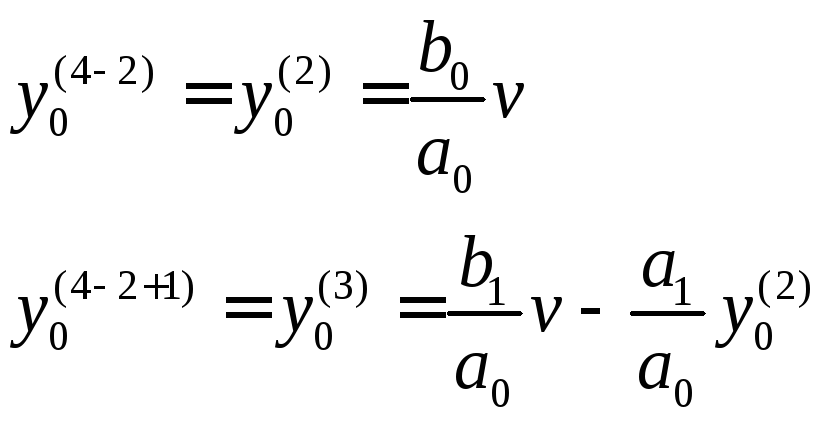(1.144)

Если воспользоваться ранее заданными значениями для коэффициентов уравнения(1.116) и принять v = .25, то начальные условия получаются следующими: ,Эти данные являются начальными условиями для переменных.

На рис.1.59 показаны переходные процессы, полученные решением системы (1.143) с начальными данными для производных

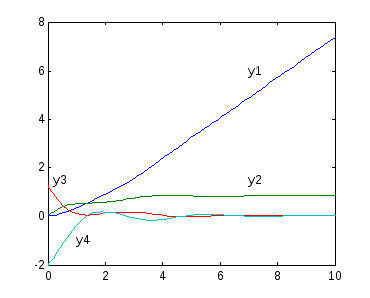
Рис. 1.59. Переходные процессы

Видно, что стечением времени третья и четвертая производные изатухают. Производнаястремится к постоянному значению, определяющему наклон неограниченно возрастающей с течением времени переменной.

9. Синтез систем автоматического регулирования

Рассматривается возможность решения задачи параметрического синтеза САР на основе алгоритмов метода эффективных полюсов и нулей. Алгоритмы метода позволяют автоматизировать процесс нахождения параметров, обеспечивающих заданные показатели качества проектируемой системе. Для этой цели алгоритмы метода дополняются процедурами оптимизации, позволяющими выполнять направленный поиск параметров.

Рассмотрена также методика синтеза последовательных корректирующих устройств с помощью логарифмических частотных характеристик.

9.1. Основные положения метода эффективных и нулей

Метод эффективных полюсов и нулей (МЭПН) ориентирован на .преимущественное использование ЭВМ для решения задач проектирования САР. Метод позволяет решать задачу оптимизации на ЭВМ некоторого критерия качества при наличии большого числа ограничений и варьируемых параметров. Метод имеет простые алгоритмы, составленные из коэффициентов характеристического уравнения:

(1.145) Простота алгоритмов создает возможность не трудоемко вручную выполнять расчеты показателей качества переходных процессов. В результате расчета определяются исходные значения параметров элементов САР, используемых далее для выполнения расчетов на ЭВМ. Расчеты с использованиемметода являются приближенными,погрешности могут достигать 10-30 %. Поэтому на заключительном этапе расчета требуется численное моделирование.Метод разработан Климовым В.А. в 1980-1985г.г. и опирается на корневые показатели качества [5].

Метод можно применять лишь в том случае, если выполнена исходная предпосылка - требование по колебательности системы (1.125). Данное требование имеет вид

μ  4.89. (1.146)

Область изменения параметров элементов системы, где выполняется требование (1.146) называется рабочей областью. Так как переменных параметров в системе может быть много, то рабочая область в общем случае ограничиваются многомерной поверхностью. Если переменных параметров два, то рабочая область будет представлять собой часть плоскости.

Для системы третьего порядка уравнения границ рабочей области имеют вид:

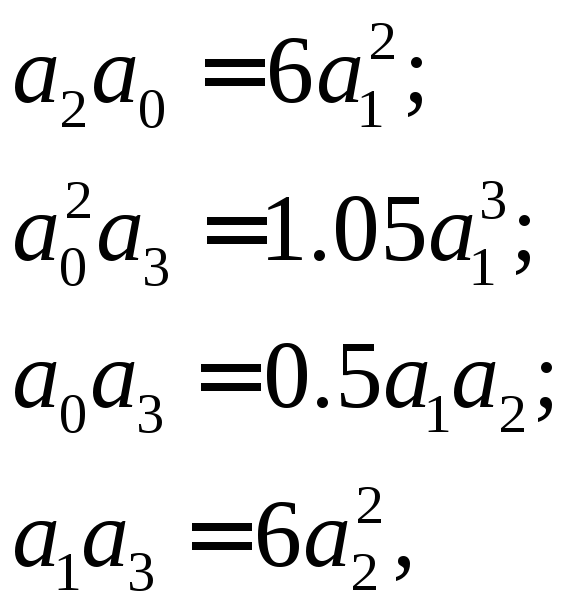(1.147)

где коэффициенты характеристического уравнения.

Расчет границ рабочей области по приведенным соотношениям целесообразно выполнять при ручном расчете систем. Если рассчитывается система, имеющая порядок выше третьего, то для выполнения ручного расчета рекомендуется отбросить члены уравнения с производными выше третьего порядка и рассчитать упрощенные границы рабочей области

Внутри рабочей области левая часть выражений (1.147) должна быть меньше правой части, т.е. в системе (1.147) вместо знака равенства должен применяться знак «меньше». Построение рабочей области в плоскости двух параметров применяется, как правило, при ручном расчете. При этом по одной оси откладывается коэффициент усиления разомкнутой системы, а по другой оси тот параметр, который оказывает наибольшее влияние на динамику процессов, например, параметры корректирующего элемента.

В рабочей области располагаются точки, соответствующие различным значениям параметров, откладываемым по осям системы координат. Эти точки называются рабочими.

Результаты ручного приближенного расчета позволяют определить возможные диапазоны изменения переменных параметров системы необходимые для решения задачи параметрического синтеза на ЭВМ. В этой задачи должны использоваться уже полные уравнения систем без отбрасывания членов с высшими производными. Задача синтеза рассматривается ниже.

Если для расчета САР применяется ЭВМ, то рабочая область не строится. Координаты пробных рабочих точек берутся либо случайно, либо с помощью различных оптимизационных процедур. Очевидно, что для каждого варианта рабочей точки требуется проверка выполнения исходной предпосылки метода. Для этой цели в МЭПН разработаны алгоритмы для определения запасов устойчивости – чисел

m₂ = 0.17Δ₂, Δ₂ = a₀a₂/a₁²;

m₃ = 0.17Δ₃ [1+9Δ₂+2Δ₂²+0.4Δ₂³], Δ₃ = a₃a₁/a₂²; (1.148)

m₄ = 0.17Δ₄ [1+9Δ₃+2(1+6Δ₂)Δ₃²+0.4(1+100Δ₂)Δ₃³], Δ₄ = a₄a₂/a₃²;

m₅ = 0.17Δ ₅ [1+9Δ₄+2(1+6Δ₃)Δ₄²+0.4(1+100Δ₃)Δ₄³], Δ₅ = a₅a₃/a₄²; ……………………………………………………………………….

m_n = 0.17Δ_n [1+9Δ_n-1+2(1+6Δ_n-2)Δ_n-1²+0.4(1+100Δ_n-2)Δ_n-1³], Δ_n=a_na_n-2/a_n-1²,

где n – порядок уравнения (1.145).

Рабочая точка находится в рабочей области, если числа

m_j < 1, ( j =2,…, n ). (1.149)

Каждой рабочей точке может соответствовать апериодический или колебательный переходный процесс. Для определения формы процесса необходимо рассчитать величину показателя

ρ = 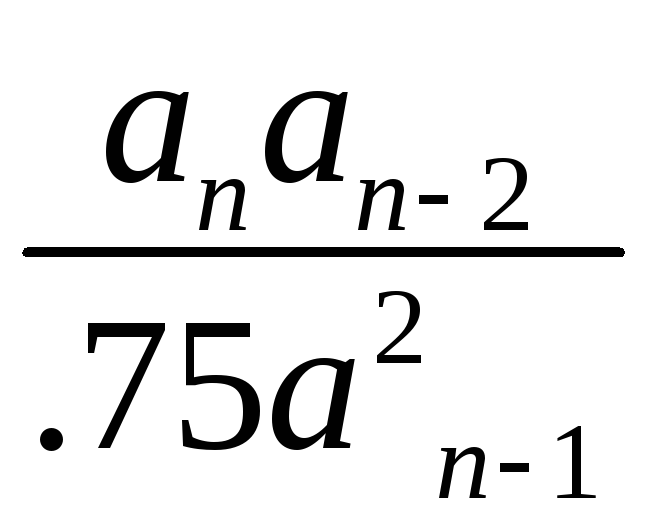. (1.150)

Если выбранной рабочей точке соответствует значение ρ >1, то форма переходного процесса будет колебательной. Причем колебательность усиливается с увеличением показателя. Если ρ < 1, то переходный процесс будет апериодическим.

Выражение (1.150) позволяет получить уравнение кривой, разделяющей рабочую область на две подобласти. В одной из них будут располагаться только колебательные процессы, а в другой - только апериодические.

Для этого необходимо в (1.150) принять ρ = 1 и далее записать

Метод эффективных полюсов и нулей предлагает простые алгоритмы для оценки показателей качества переходных процессов:

- время переходного процесса;

- максимальные отклонения координат и их производных.

Расчет времени переходного процесса выполняется по следующим формулам:

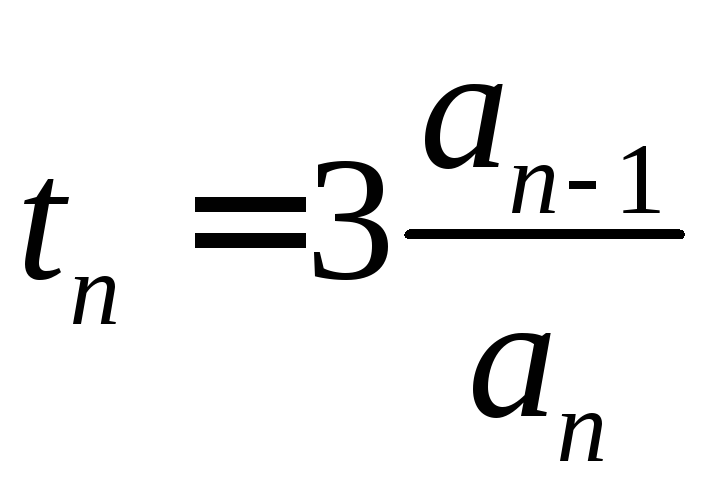, если показатель ρ < 1, (1.151)

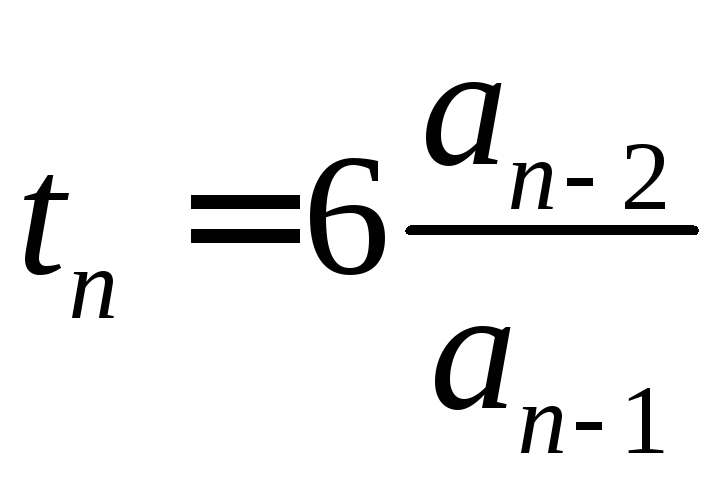, если показатель ρ > 1.

Выражения (1.151) позволяют нанести на плоскость рабочей области кривые, соответствующие равным значениям времени переходных процессов.

Для этого в выражениях (1.151) необходимо задать значения и далее получить уравнения кривых.

При рассмотрении алгоритмов для расчета максимальных отклонений координат и их производных будем иметь в виду следующее уравнение САР

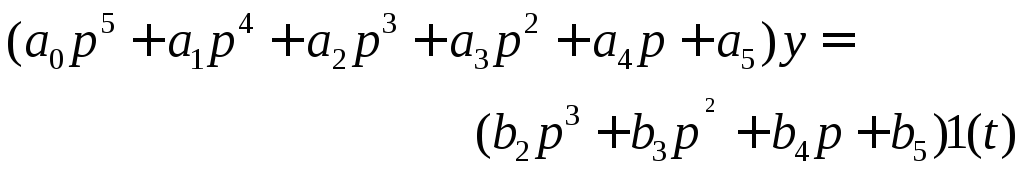. (1.152)

Для расчета величины максимального отклонения координаты применяются следующие формулы:

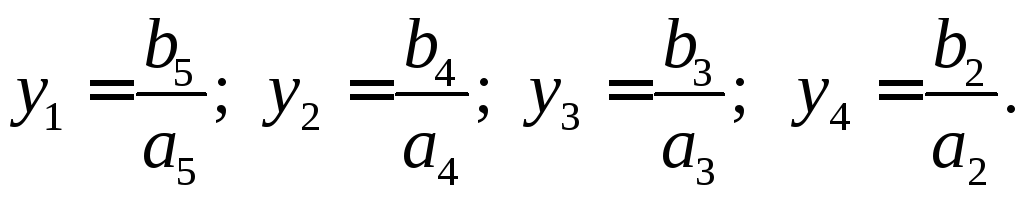(1.153)

Для определения максимального отклонения требуется сравнить величины приведенных отношений (1.153) и из них выбрать наибольшее.

Видно, что анализируемые отношения составлены из коэффициентов уравнения (1.152), принадлежащих одинаковым производным.

Для расчета величины максимального отклонения скорости ý = ý необходимо умножить левую и правую части уравнения (1.152) на оператор . После этого действия уравнение принимает вид:

=

. (1.154)

Далее необходимо составить отношения из коэффициентов левой и правой частей уравнения (1.154) (коэффициенты должны принадлежать одинаковым производным), сравнить величины отношений и определить из них наибольшее. Эти соотношения имеют вид:

ý=; ý=ý=ý=(1.155) Для расчета наибольшего отклонения ускорения - ÿ, то необходимо умножить левую и правую части уравнения (1.152) наи далее выполнить уже известные операции.

9.2. Синтез CАР на ЭВМ

Параметрический синтез является одной из основных задач проектирования САР. Формулировка задачи: задана структурная схема системы и уравнения элементов. Известны также возможные диапазоны изменений переменных параметров САР. Требуется так определить численные значения этих параметров, чтобы удовлетворялся некоторый критерий качества при выполнении требований по другим показателям.

Например, в качестве критерия качества может использоваться время переходного процесса: , а в качестве других показателей, выполняющих роль ограничений, могут выступать: максимальные отклонения координат и их скоростей, затухание за период и др. Следует указать, что в качестве критерия и ограничений могут применяться массовые, энергетические и др. характеристики элементов системы.

Возможные диапазоны изменения переменных параметров определяются в результате ручного расчета, выполняемого по упрощенной модели. Обычно этой моделью являются упрощенные до третьей степени уравнения САР. Ранее указывалось, что МЭПН может применяться для решения задачи оптимизации на ЭВМ некоторого критерия качества при наличии большого числа ограничении и переменных параметров. Очевидно, что такая оптимизация предполагает расчет и оценку большого количества вариантов систем. Сейчас уже можно понять, что такая задача вполне реализуема, так как в методе разработаны достаточно простые алгоритмы для расчета показателей качества регулирования. Время на расчет системы, соответствующей одной рабочей точки составляет доли секунды. Однако, в рабочей области рабочих точек бесконечное множество и поэтому необходимо предложить какую-то схему выборки рабочей точки с целью решения задачи синтеза по ограниченному количеству вариантов. В рассматриваемой задаче параметрического синтеза предлагается применить случайно-направленный поиск. Предварительно целесообразно рассмотреть простую схему поиска.

Схема случайного поиска состоит в том, что по случайному закону выбираются численные значения переменных параметров и координаты рабочей точки в рабочей области (рис.1.60,а). На рисунке z₁ и z₂ переменные параметры системы (например, z₁ - постоянная времени корректирующего элемента, z₂ - коэффициент усиления). Обозначения: z₁^max  z₁^min, z₂^min  z₂^max – диапазоны возможных изменений параметров z₁ и z₂; z_1,0 и z_2,0 – некоторые случайно выбранные значения параметров в области Q₀.

Для реализации варианта случайной выборки координат рабочей точки применяются следующие формулы:

z_1,0 = z₁^min + RAND*(z₁^max – z₁^min); (1.156)

z_2,0 = z_2,min + RAND*(z₂^max – z₂^min),

где RAND – процедура получения случайного числа из диапазона [0,1].

Если найденные значения z_1,0 и z_2,0 удовлетворяют решаемой задаче параметрического синтеза, то они становятся координатами рабочей точки в рабочей области. Необходимо отметить, что в схеме поиска использованы только два переменных параметра z₁ и z_2.

Схема случайно-направленного поиска (рис.1.60,б) состоит в том, что процессу расчета численных значений параметров z_1,0 и z_2,0 по случайному закону придается направленное движение. Предположим, что по схеме случайного поиска в области Q₁ выполнено некоторое ограниченное количество вариантов расчетов. В результате оказалось, что координаты точки 1 соответствуют лучшему варианту, т.е. показатели качества системы, в расчете которой использованы численные значения постоянной времени корректирующего элемента и коэффициента усиления, соответствующие этой точке оказались лучше, чем в других вариантах. Если требуется дальнейшее улучшение показателей качества ( или дальнейшая оптимизация некоторого критерия), то расчеты необходимо продолжить. Для этого область Q₁ перемещается в сторону точки 1 так, чтобы эта точка стала центром области. В результате получится область Q₂ с новыми численными значениями координат: Z₁^max, Z₁^min, Z₂^max, Z₂^min. Эти новые значения получаются геометрическим расчетом с использованием координат области Q₁.

Д

алее в областиQ₂ также выполняется некоторое количество вариантов расчетов и последующие уже известные действия. В результате получается точка 2, по физическому смыслу аналогичная точке 1 и новая область поиска Q₃. По такой схеме осуществляется направленный поиск в рабочей области значений переменных параметров до выполнения требований по качеству регулирования. Время поиска оказывается не большим. На рис.1.61 представлена схема решения задачи синтеза на ЭВМ. Схема отражает последовательность действий (алгоритм) для расчета переменных параметров системы и показателей качества регулирования. Очевидно, что алгоритм предназначен для составления программы решения задачи синтеза на ЭВМ. Данная последовательность содержит 14 позиций:

1 – задание исходных данных, включающих параметры и константы, не изменяющие своих значений в процессе реализации алгоритма;

2 - задание диапазонов изменения переменных параметров. Максимальные и минимальные значения для параметров (диапазоны их изменения) определяются в результате ручного расчета, который выполняется приближенно и по упрощенным моделям;

3 - расчет случайных значений переменных параметров. Применяются формулы (1.156);

4 - расчет численных значений для коэффициентов характеристического уравнения с использованием полученных случайных значений переменных параметров;

5 - проверка исходной предпосылки метода. Применяются формулы (1.148). Исходная предпосылка выполняется, если в результате расчета выполняются неравенства (1.149). Если неравенства не выполняются, то алгоритм возвращает расчет к позиции 3.

6 - расчет показателя выполняется для определения формы переходного процесса, соответствующего выполненной выборки переменных параметров. Применяется формула (1.150);

7 - определение времени переходного процесса. В зависимости от величины показателя ρ применяется одна из формул (1.151);

8 - выполняется проверка выполнения ограничения . Если ограничение не выполняется, то алгоритм возвращает расчет к позиции 3;

9 - расчет коэффициентов правой части уравнения системы;

10 - расчет максимального отклонения координаты выполняется по формулам (1.153);

11 - проверка выполнения ограничения по величине максимального отклонения. Заданная величина возможного отклонения координаты определяется техническим заданием на разрабатываемую систему. В случае не выполнения ограничения алгоритм возвращает расчет к позиции 3.

Позиции 12 и 13 похожи на предыдущие две, поэтому подробно пояснять их не требуется. Позиция 14 предполагает размещение в алгоритме других ограничений и сопутствующих им расчетов, связанных с энергетическими, массовыми, температурными и др. характеристиками объектов регулирования

После выполнения 14 позиции результаты расчета (координаты рабочей точки и соответствующие ей значения параметров) по желанию расчетчика могут быть выведены на печать. Если результаты оказались недостаточными, то алгоритм возвращает расчет к позиции 2, в которой предыдущая область поиска случайных значений переменных параметров Q₁ должна переместиться и стать областью Q₂. Центром этой области должна стать рабочая точка предыдущей области . Для реализации этого необходимо геометрически пересчитать максимальные и минимальные значения для переменных параметров. Это будет началом случайно-направленного поиска.

1. Константы

2. Задание интервалов Zi min, Zi max, i = 1,…,k

3..Выбор значений Z,

4. Расчет

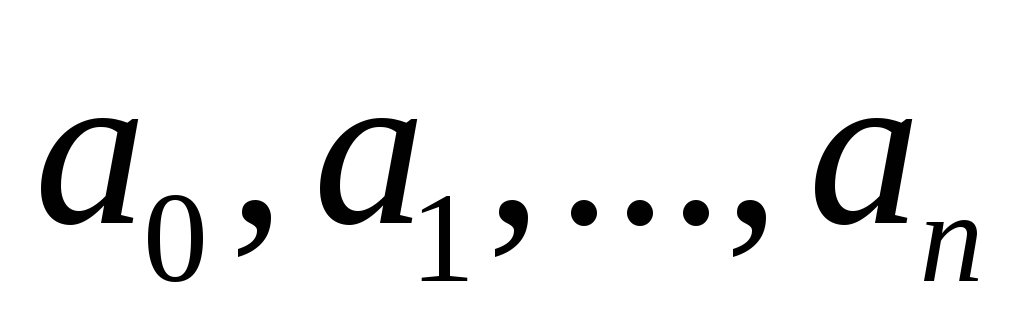
5 нет .Проверка mj < 1,

да

7.. Расчет времени

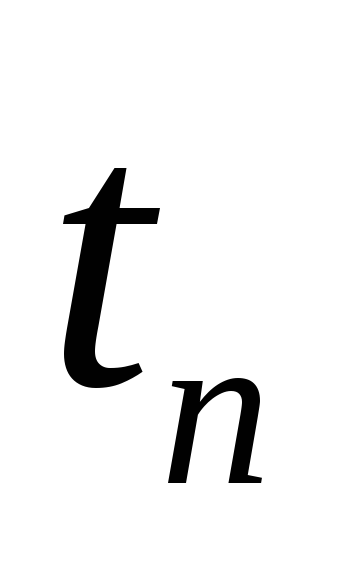
8.. Проверка

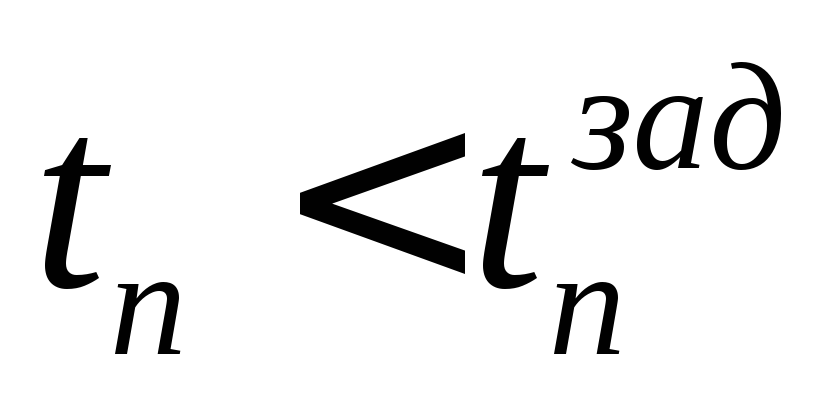
да нет

9. Расчет

10. Расчет отклон.

11. Проверка у max < y зад

Рис.1.45. Комплексная плоскость расположения корней характеристического уравнения

да

нет

12.Расчет отклон. ý

Печать

13 Проверка ý max < ý зад

данет

14Проверка других ограничений

нет

Рис.1.61. Схема решения задачи синтеза на ЭВМ

9.3. Синтез корректирующих устройств с помощью ЛАХ

При проектировании САР многие элементы системы заранее предопределены техническим заданием, и они составляют так называемую неизменяемую часть системы. В эту часть входят: объект управления, усилитель, исполнительное устройство, элементы сравнения. Показатели качества системы, содержащей только неизменяемую часть, невысокие. Для повышения качества регулирования необходимо в состав элементов системы включать корректирующие устройства. Однако перед включением необходимо определить само устройство, как минимум его передаточную функцию. Расчет передаточной функции представляет собой задачу синтеза корректирующих устройств. При синтезе последовательных и параллельных корректирующих устройств обычно задают: порядок астатизма; перерегулирование; время переходного процесса; максимальное ускорение, которое может обеспечить исполнительное устройство системы. В качестве типового воздействия рассматривают скачкообразный сигнал.

9.3.1. Методика расчета последовательных корректирующих устройств. Для формирования методики применяется структурная схема системы, представленная на рис.1.62. Схема содержит неизменяемую часть системы с передаточной функцией и корректирующее звено с передаточной функцией. Предположим, что корректирующее устройство найдено, и показатели качества системы соответствуют желаемым. В этом случае передаточная функция разомкнутой системыможет рассматриваться как желаемая передаточная функция, определяющая желаемые частотные характеристики.

Учитывая сказанное, запишем выражение для желаемой логарифмической амплитудно-частотной характеристике (ЛАХ)

,

где и- логарифмические частотные характеристики неизменяемой части системы и корректирующего устройства.

Поскольку желаемая ЛАХ - и ЛАХ неизменяемой части системы -известны, то можно записать формулу для определения ЛАХ корректирующего устройства

. (1.157)

Полученная формула позволяет указать последовательность в расчете последовательного корректирующего устройства:

1

. Построение желаемой ЛАХ разомкнутой системы и ЛАХ неизменяемой части системы;

2. Графическое решение уравнения (1.157), т. е. определение ЛАХ корректирующего устройства путем вычитания из желаемой ЛАХ ( которая строится в соответствии заданными показателями качества процесса) ЛАХ неизменяемой части системы;

3. Определение по виду полученной ЛАХ передаточной функции корректирующего устройства;

4. Проверка правильности выполненного расчета корректирующего элемента. Выполняется построением и оценкой качества переходного процесса

9

.3.2 Диаграмма равных значений вещественных частотных характеристик.

Применяется для построения желаемой логарифмической амплитудно-частотной характеристики. Ниже получим выражение для построения кривых зависимостей, образующих диаграмму.

Известно, что 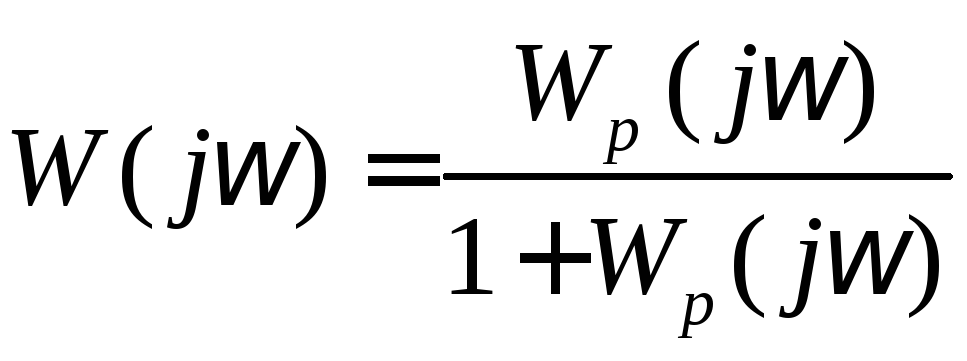, гдечастотная передаточная функция разомкнутой системы.

Далее можно записать

Учитывая, что предыдущее выражение можно записать в виде

.

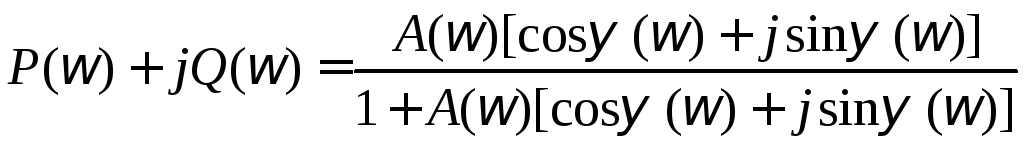Далее можно выделить вещественную часть

.

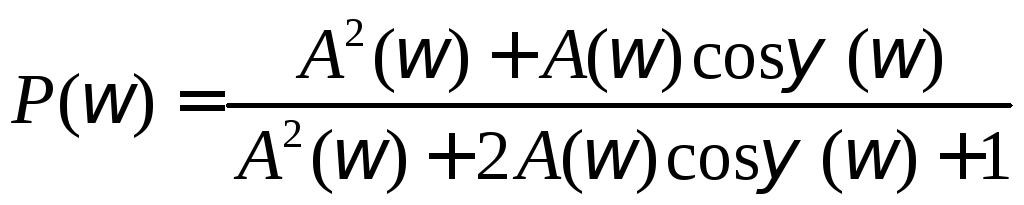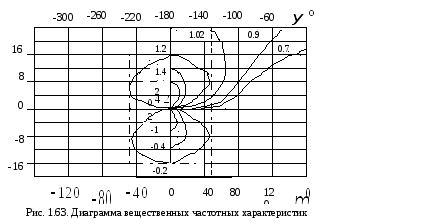
Полученное выражение позволяет определить геометрическое место точек, соответствующее фиксированным значениям вещественной частотной характеристики в координатной плоскости, где по оси ординат откладывается, а по оси абсцисс - смещение по фазеразомкнутой системы. По этой же оси (в нижней части диаграммы) откладывается запас устойчивости по фазе.

Небольшое количество линий, соответствующих … показано на рис.1.63. Приведенные на рисунке линии являются не точными и отражают лишь принцип построения диаграммы. Точные кривые представлены в известной литературе [2]. На практике диаграмма применяется при расчете желаемой логарифмической характеристики.

9.3.3. Построение желаемой ЛАХ.Желаемую логарифмическую характеристику строят с учетом требований, предъявляемых к качеству переходного процесса. Примем, что переходный процесс в системе вызван единичным ступенчатым входным воздействием Требуется, чтобы перерегулирование и время переходного процесса не превосходили заданных величин =26% и =0.63c. При этом принимается, что исполнительный механизм обеспечивает перемещение регулирующего органа с максимальным ускорением =. Задаются также порядок астатизмаи коэффициент передачи неизменяемой части системы=100.

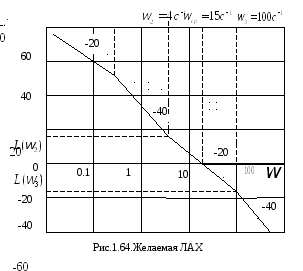
График желаемой ЛАХ охватывает области низких, средних и высоких частот. В области низких частот прохождение ЛАХ определяется уравнением . Уравнение соответствует асимптоте с наклоном 20 дб/дек, рис.1.64. Построение асимптоты в области средних частот опирается на исходные данные и .

В области средних частот ЛАХ должна пересекать ось абсцисс в точке и иметь наклон. Выбор частоты среза осуществляется на основании неравенства,в котором

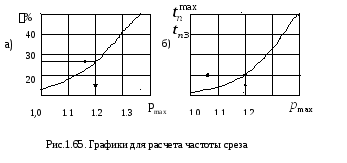
В результате получается,Значение для частотыопределяется из графиков на основании заданных значений перерегулирования = 26% и времени переходного процесса , рис.1.65

С учетом заданного перерегулирования из графика (рис.1.65,а) находится и далее, с учетомиз графика (рис.1.65,б) находится величина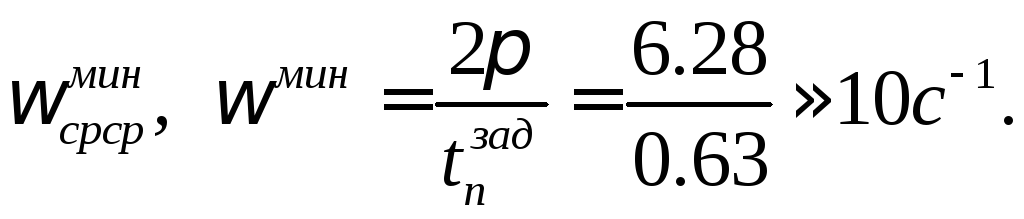Следовательно, 10. Можно принять. Полученные данные для частот, определяют граничные значения:, смещение по фазеи запас устойчивости по фазе, рис.1.63. В данном случае приграничные значения характеристик:и. Смещение по фазе, запас устойчивости по фазе. Таким образом, для размещения асимптоты имеем следующие данные: наклон,, на левой границе асимптоты, на правой границе. И еще одно условие. Обычно область средних частот охватывает диапазон частот не менее одной декады.

В области высоких частот форма желаемой ЛАХ принимается такой же, как и форма ЛАХ неизменяемой части. Сопряжение низкочастотной и среднечастотной ЛАХ производится с помощью прямых, наклон которых не должен отличаться от наклона соседних асимптот более, чем на 20 и 40 дб.

При построении ЛАХ сопряжение должно выполняться так, чтобы для модулей, из интервала , выдерживалось бы требуемое значение запаса устойчивости по фазе.

Для проверки выполнения этого условия необходимо предварительно определить вид передаточной функции для построенной желаемой ЛАХ. Передаточная функция определяется с помощью таблицы 2 [2]. В таблице:

Выполним указанную проверку. Построенная характеристика имеет структуру 20 - 40 – 20 – 40 и соответствует передаточной функции

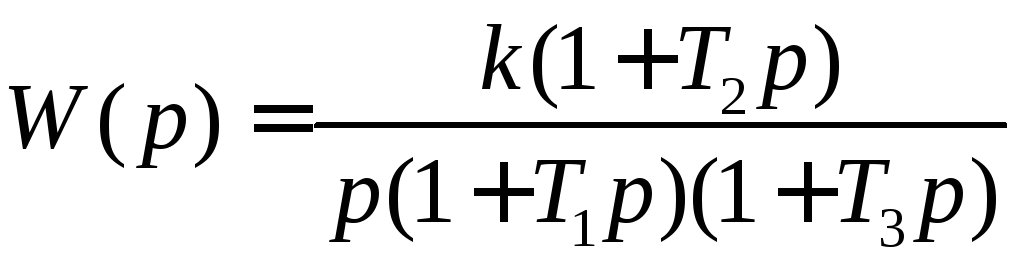, (1.158)

Таблица 2

Тип	Вид передаточной функции	Структура ЛАХ
1 2 3 4		20 – 40 – 20 – 40 20 – 60 – 20 – 40 20 – 40 – 20 – 60 20 – 60 – 20 - 60

Выражение для расчета смещения по фазе для передаточной функции (1.158) имеет вид

. (1.159)

Расчет запаса устойчивости по фазе выполняется для двух частот и:и. Если окажется, чтоито желаемая ЛАХ приемлема и соответствует заданным требованиям по перерегулированию и времени переходного процесса. В противном случае требуется увеличить диапазон средних частот.

Выражение (1.159) позволяет выполнить необходимые расчеты:

=,.

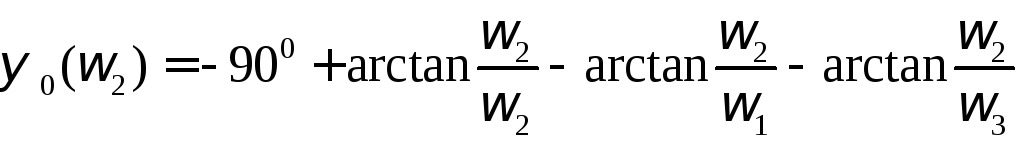Результаты расчета показывают, что требование по запасу устойчивости в данном расчете выполняются, так как требуемый запас устойчивости , в расчете,.

9.3.4. Определение передаточной функции корректирующего элемента. Выше отмечалось, что вид передаточной функции корректирующего элемента определяется в результате графического решения уравнения (1.157). Однако для этого кроме желаемой ЛАХ необходимо иметь ЛАХ неизменяемой части системы. Пусть передаточная функция неизменяемой части системы имеет вид

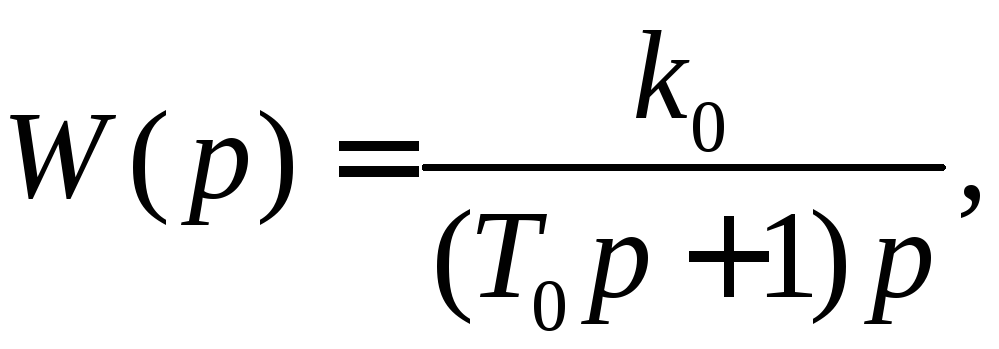
где ,

На рис.1.66 изображены: ранее построенная желаемая логарифмическая амплитудно-частотная характеристика 2, ЛАХ неизменяемой части системы 1 и ЛАХ корректирующего элемента 3. Логарифмическая характеристика корректирующего элемента получена в результате графического вычитания характеристики 1 из характеристики 2.

Для построения ЛАХ неизменяемой части системы необходимо выполнить следующие действия:

записать выражение для АЧХ,

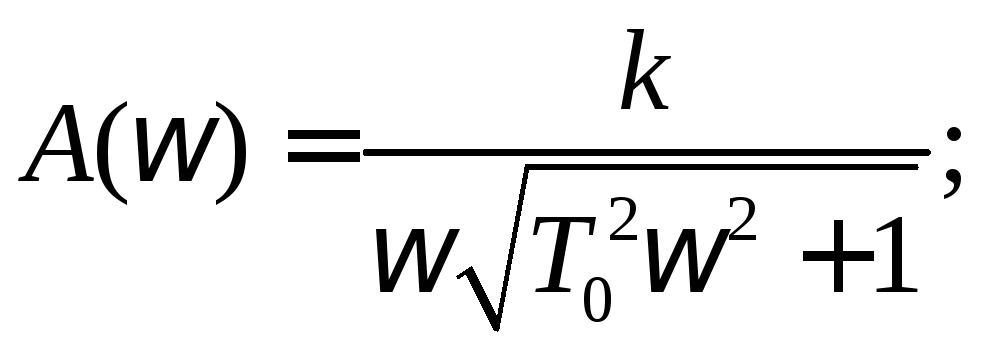
определить сопрягающую частоту,

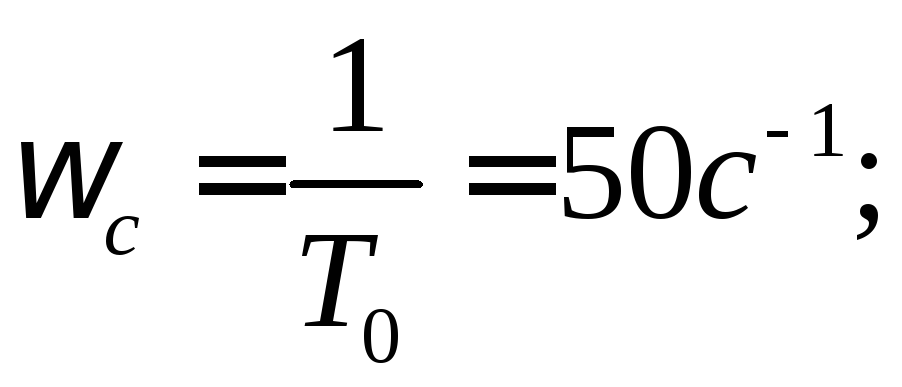
получить выражение для асимптоты, которая должна быть до сопрягающей частоты,

получить выражение для асимптоты, которая должна быть после сопрягающей частоты, .

Далее необходимо (рис.1.66) выполнить графическое вычитание из желаемой характеристики (2) ЛАХ неизменяемой части системы (1).

После вычитания по конфигурации ЛАХ корректирующего элемента (3) определяется вид передаточной функции корректирующего элемента.

Изобразим ЛАХ звена, имеющего передаточную функцию

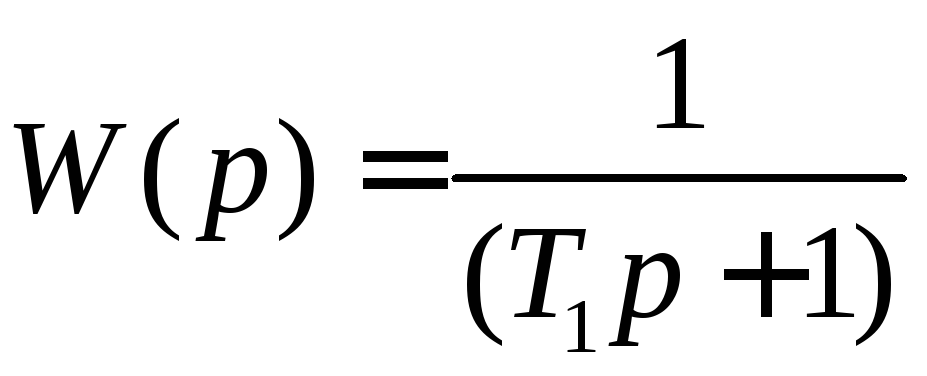, . (1.160)

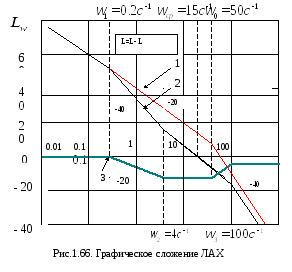
Частотная передаточная функция 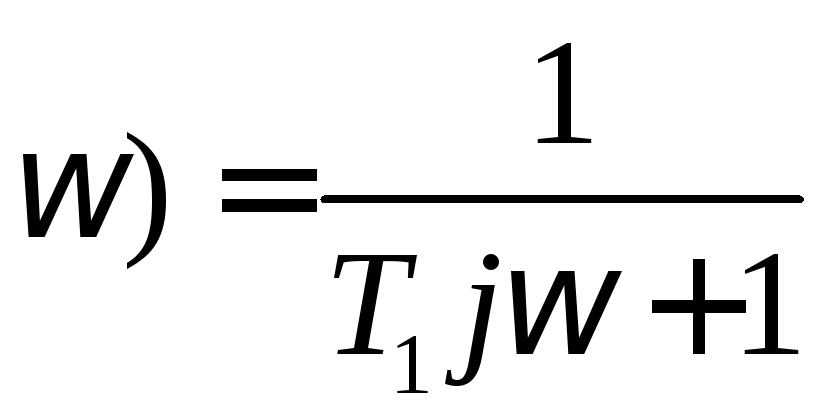. Сопрягающая частотаУже очевидно, что передаточная функция (1.63) соответствует первым двум асимптотам, охватывающим диапазон частот. При этом вторая асимптота по построению имеет наклон – 20 дб/дек. Следующая асимптота имеет наклон 0 дб/дек. Следовательно, в числитель формулы (1.63) необходимо дописать множитель, в котором. Так как, то. Следующая асимптота имеет наклон + 20 дб/дек. Следовательно, опять в числитель формулы необходимо добавить множитель, в котором. Так как, тоПоследняя асимптота не имеет наклона, следовательно, в знаменатель формируемой передаточной функции необходимо добавить множитель, в котором. Так как, топри этом, вторая асимптота по построению имеет наклон – 20 дб/дек. В итоге вид передаточной функции для корректирующего элемента оказывается следующим.

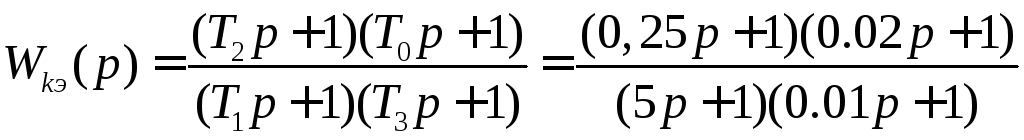Л и т е р а т у р а 1. Воронов А.А. Основы теории автоматического регулирования. – М.: Высшая школа,1977, 518с. 2. Бесекерский В.А. Попов Е.П. Теория систем автоматического управления. – Спб.: Профессия, 2007, 730с. 3. Выгодский М.Я. Справочник по высшей математике. – М: Наука, 1966, 730с. 4.Бесекерский В.А., Орлов В.П. Проектирование следящих систем малой мощности. - Л.: Судпромгиз, 1958, 500с. 5.Климов В.А. Лекус В.Д. Проектирование и расчет динамических систем. - Л.: Машиностроение, 1974, 350с.

C о д е р ж а н и е Стр

1. Основные сведенитя об автоматизации 2

1.1. Основные понятия и определения 2 1.2. Принципы управления и определение САР 8 1.3. Основные элементы и классификация САР 12 1.4. Требоваеия к САР 14

1.5. Линейные законы регулирования 16 2. Уравнения элементов САР 19

2.1. Линеаризация нелинейных уравнений САР 21

2.2. Формы записи линеаризованных уравнений элементов САР 24

3. Временные и частотные характеристики динамических звеньев 27 3.1. Понятие о динамическом звене 27

3.2. Временные характеристики динамических звеньев 29

3.3. Статические характеристики звеньев 31

3.4. Частотные характеристики динамических звеньев 32

4. Типовые динамические звенья 35

4.1. Позиционные звенья 36

4.2. Дифференцирующие и интегрирующие звенья 43

4.3. Трансцендентное звено 49 5. Логарифмические частотные характеристики 51

5.1. Система координат. Простейшие ЛАХ 51

5.2. Логарифмические характеристики динамических звеньев 53

5.3. Построение ЛАХ сложных передаточных функций 57

6. Уравнения систем автоматического регулирования 60

6.1. Передаточные функции САР 60

6.2. Получение уравнений САР 61

6.3. Преобразование структурных схем 63

6.4. Уравнения состояния 65 7. Устойчивость линейных систем 68

7.1. Общие сведения об устойчивости линейных систем 68

7.2. Критерий устойчивости Гурвица 72

7.3. Критерий устойчивости Михайлова 73

7.4. Критерий устойчивости Найквиста 75

7.5. Построение области устойчивости 76 Оценка качества регулирования 78

8.1. Статическая точность систем регулирования 78

8.2. Оценка запаса устойчивости и быстродействия систем 83

8.3. Учет начальных условий при расчете переходных процессов 90 9. Синтез систем автоматического регулирования 94

9.1. Основные положения метода эффективных полюсов и нулей 95

9.2. Синтез САР на ЭВМ 98

9.3. Синтез корректирующих устройств с помощью ЛАХ 102

УДК 681.5(075.8)

ББК 32.965я73

Э67

Рассмотрены основы теории линейных систем автоматического регулирования, включающие принципы построения, описание систем, устойчивость и методы оценки качества регулирования, а также метод решения задачи многопараметрического синтеза на ЭВМ с применением процедур оптимизации для достижения заданных показателей качества регулирования.

Рецензенты: 1. Доктор технических наук проф. КондрашковаГ.А.

2. Доктор технических наук проф. Полякова Е.В.

115