
5. Логарифмические частотные характеристики
5.1. Система координат. Простейшие ЛАХ
Lw
= 20![]() |
|![]() |
=
|
=
![]() .
.
Значения для Lw выражаются в децибелах. Бел представляет собой логарифмическую единицу, соответствующую десятикратному увеличению мощности. Два бела соответствует увеличению мощности в 100 раз, три бела – в 1000 раз и т. д. Децибел равен одной десятой части бела.
Для построения
ЛАХ используется система координат,
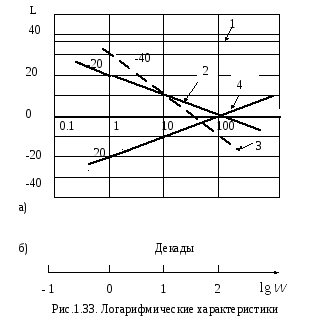
рис.1.33 . По оси абсцисс откладывается
угловая частота
![]() (размерность
(размерность![]() )
в логарифмическом масштабе (рис.1.33,а).
Для этой цели может использоваться
специальная логарифмическая бумага
или логарифмическая шкала.
)
в логарифмическом масштабе (рис.1.33,а).
Для этой цели может использоваться
специальная логарифмическая бумага
или логарифмическая шкала.
Справка.
Логарифмическая шкала неравномерная.
Строится так: на осях прямоугольной
системы координат
![]() откладываются десятичные логарифмы
чисел
откладываются десятичные логарифмы
чисел![]() и
и![]() :
:![]() Через
точки деления, имеющие числовые пометки
Через
точки деления, имеющие числовые пометки![]() и
и![]() проводятся прямые параллельные осям
проводятся прямые параллельные осям![]() и
и![]() .
.
По оси ординат
откладывается
![]() в децибелах
в децибелах![]() .
Ось абсцисс должна проходить через
точку 0 дб., что соответствует значению
.
Ось абсцисс должна проходить через
точку 0 дб., что соответствует значению![]() =1.
Иногда по оси абсцисс откладывается не
сама частота (рис.1.33,а), а ее десятичный
логарифм, (рис.1.33,б ). Единицей приращения
частоты при построении ЛАХ является
одна декада. Ось ординат может пересекать
ось абсцисс в произвольном месте. На
рис. 1.33,а ось ординат пересекает ось
абсцисс в точке
=1.
Иногда по оси абсцисс откладывается не
сама частота (рис.1.33,а), а ее десятичный
логарифм, (рис.1.33,б ). Единицей приращения
частоты при построении ЛАХ является
одна декада. Ось ординат может пересекать
ось абсцисс в произвольном месте. На
рис. 1.33,а ось ординат пересекает ось
абсцисс в точке![]() .
Необходимо помнить, что точка
.
Необходимо помнить, что точка![]() расположена на оси частот слева в
бесконечности, так как
расположена на оси частот слева в
бесконечности, так как![]() ∞.
∞.
Главным достоинством логарифмических амплитудных частотных характеристик является возможность их построения во многих случаях без объемной вычислительной работы. Это относится в основном к случаям, когда частотная передаточная функция может быть представлена в виде произведения сомножителей. Рассмотрим примеры построения простейших ЛАХ.
1. Пусть
![]() тогда
тогда
![]() .
Логарифмическая характеристика
представляет собой прямую параллельную
оси абсцисс (см. прямая 1 на рис. 1.33,а).
.
Логарифмическая характеристика
представляет собой прямую параллельную
оси абсцисс (см. прямая 1 на рис. 1.33,а).
2
Рис.![]() тогда
тогда![]() .
Нетрудно видеть, что
.
Нетрудно видеть, что![]() - прямая линия. Если
- прямая линия. Если
![]()
![]() ,
то
,
то
![]() .
Если
.
Если
![]() то
то![]() =0.
Далее нетрудно построить прямую 2
(рис.1.33,а)c
координатами
=0.
Далее нетрудно построить прямую 2
(рис.1.33,а)c
координатами
![]()
![]() и
и![]() .
Видно, что с увеличением частоты на одну
декаду
.
Видно, что с увеличением частоты на одну
декаду![]() уменьшается на 20
уменьшается на 20![]() ,
т.е. асимптота имеет отрицательный
наклон равный 20дб/дк. Этот факт на графике
отмечен цифрой «-20». Отметим, что частота,
при которой
,
т.е. асимптота имеет отрицательный
наклон равный 20дб/дк. Этот факт на графике
отмечен цифрой «-20». Отметим, что частота,
при которой![]() (при этом
(при этом![]() )
называется частотой среза и обозначается
)
называется частотой среза и обозначается![]() .
.
3. Далее рассмотрим
случай, когда
![]() С
опорой на предыдущий случай можем
записать
С
опорой на предыдущий случай можем
записать![]() .
Видно, что в данном случае ЛАХ представляет
собой прямую линию с отрицательным
наклоном равным -40
.
Видно, что в данном случае ЛАХ представляет
собой прямую линию с отрицательным
наклоном равным -40![]() (
прямая 3 на рис.1.33,а ).
(
прямая 3 на рис.1.33,а ).
4. Пусть
![]() ,
тогда
,
тогда![]() .
Если
.
Если
![]()
![]() ,
то
,
то
![]() .
Нетрудно увидеть, что
.
Нетрудно увидеть, что![]() -
это прямая линия, проходящая через
точку с координатами
-
это прямая линия, проходящая через
точку с координатами![]()
![]() и
и![]() .
Линия имеет положительный наклон +20
.
Линия имеет положительный наклон +20![]() ,
рис.1.33,а.
,
рис.1.33,а.
Аналогичным образом
можно показать, что в случае, когда
![]() ЛАХ представляет собой прямую линию с
положительным наклоном 20
ЛАХ представляет собой прямую линию с
положительным наклоном 20![]() .
Эта прямая также строится по одной
точке, имеющей координаты
.
Эта прямая также строится по одной
точке, имеющей координаты
![]() и
и
![]() .
.
5.2. Логарифмические характеристики динамических звеньев
Апериодическое звено 1 порядка. Выражение для амплитудно-частотной характеристики имеет вид
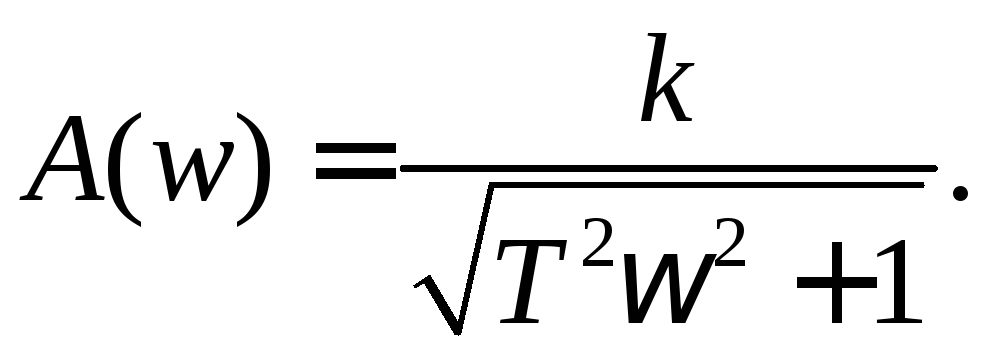 (1.70)
(1.70)
При построении
ЛАХ используется следующий прием.
Рассматриваются выражения для АЧХ при
частотах
![]() и
и![]() .
.
Если
![]() ,
то
,
то![]() ,
если
,
если![]() ,
то
,
то![]() .
Частота
.
Частота![]() называется сопрягающей и обозначается
называется сопрягающей и обозначается![]() .
.
В первом случае
![]() ,
во втором случае
,
во втором случае
![]() .
.

На рис.1.34 представлены
два варианта ЛАХ для рассматриваемого
звена. Цифрой 1 обозначен вариант,
соответствующий данным
![]()
![]() .
Цифрой 2 – вариант, соответствующий
данным
.
Цифрой 2 – вариант, соответствующий
данным
![]()
![]() с.
Видно, что постоянная времени
с.
Видно, что постоянная времени
![]() не оказывает влияния на наклон ЛАХ.
Изменяется лишь значение для сопрягающей
частоты. При Т = 1с.
не оказывает влияния на наклон ЛАХ.
Изменяется лишь значение для сопрягающей
частоты. При Т = 1с.![]()
![]() ,
при
,
при![]() .
.![]() .
.
Выполненное
построение ЛАХ является приближенным.
График ЛАХ составляется из прямых
отрезков, называемых асимптотами.
Приближенными являются соединения
асимптот в окрестности сопрягающих
частот. Например, в точке
![]()
![]() (рассматривается вариант, когда
(рассматривается вариант, когда
![]()
![]() ).
При точном построении точка
).
При точном построении точка![]() располагается
ниже на 3,03
располагается
ниже на 3,03![]() .
Это замечание следует из следующего.
.
Это замечание следует из следующего.
Вычислим значение
![]() в точке
в точке![]() Для этого используем значение частоты
Для этого используем значение частоты![]() и формулу (1.70). В результате можем
записать:
и формулу (1.70). В результате можем
записать:![]() ,
,
![]() Ошибка в этой точке составляет 3.03
Ошибка в этой точке составляет 3.03![]() .
На всем остальном протяжении влево и
вправо от сопрягающей частоты точная
ЛАХ будет отличаться от приближенной
(асимптотической) менее чем на 3
.
На всем остальном протяжении влево и
вправо от сопрягающей частоты точная
ЛАХ будет отличаться от приближенной
(асимптотической) менее чем на 3![]() Поэтому в расчетах практически всегда
применяются асимптотические ЛАХ.
Поэтому в расчетах практически всегда
применяются асимптотические ЛАХ.
Апериодическое звено 2 порядка. Выражение для амплитудно-частотной характеристики имеет вид
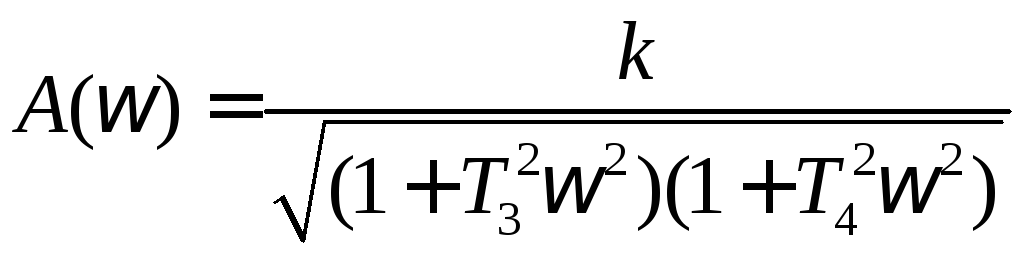 (1.71)
(1.71)
Примем, что
![]() и
и![]() и
найдем сопрягающие частоты
и
найдем сопрягающие частоты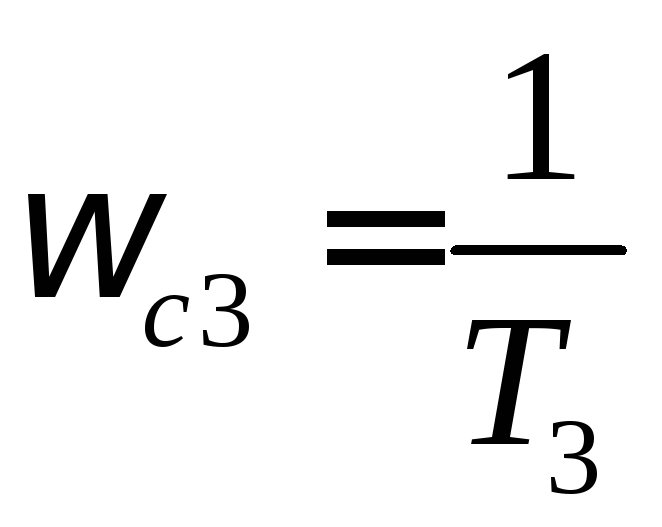 и
и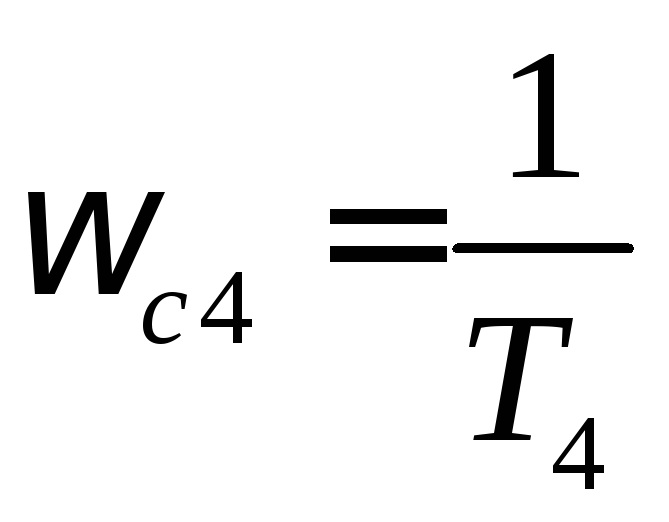 .
Расчет показывает, что
.
Расчет показывает, что![]() .
.

Далее рассматриваются три случая.
1. Если
![]() (рис.1.35
), то принимается, что в выражении (1.71)
(рис.1.35
), то принимается, что в выражении (1.71)![]() и
и![]() В этом случае формула (1.71) приобретает
следующий упрощенный вид
В этом случае формула (1.71) приобретает
следующий упрощенный вид![]() .
Следовательно, на участке изменения
частоты
.
Следовательно, на участке изменения
частоты![]()
![]() ЛАХ может быть построена по выражению
ЛАХ может быть построена по выражению![]() .
ЛАХ на этом участке представляет собой
прямую параллельную оси абсцисс ,
рис.1.35;
.
ЛАХ на этом участке представляет собой
прямую параллельную оси абсцисс ,
рис.1.35;
2. Если
![]() ,
то принимается, что
,
то принимается, что![]() ,
а
,
а![]() .
В этом случае формула ( 1.65) может быть
представлена уже в другом упрощенном
виде
.
В этом случае формула ( 1.65) может быть
представлена уже в другом упрощенном
виде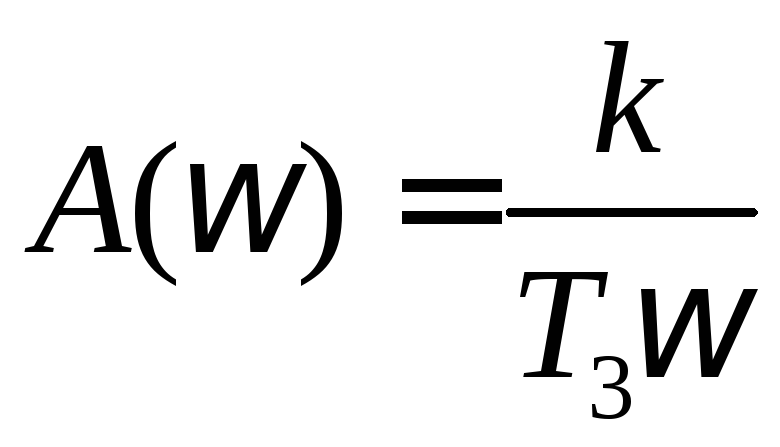 .
Выражение для построения ЛАХ получается
следующим
.
Выражение для построения ЛАХ получается
следующим![]() .
Этому выражению соответствует асимптота
с отрицательным наклоном 20дб/дек.;
.
Этому выражению соответствует асимптота
с отрицательным наклоном 20дб/дек.;
3. Если
![]() ,
то принимается, что
,
то принимается, что![]() и
и![]() .
В этом случае формула (1.71) может быть
представлена также в упрощенном виде
.
В этом случае формула (1.71) может быть
представлена также в упрощенном виде .
Выражение для построения ЛАХ получается
следующим
.
Выражение для построения ЛАХ получается
следующим![]() .
Этому выражению соответствует асимптота
с отрицательным углом наклона 40дб/дек.
.
Этому выражению соответствует асимптота
с отрицательным углом наклона 40дб/дек.
Интегрирующее звено. Выражение для амплитудно-частотной характеристики имеет вид
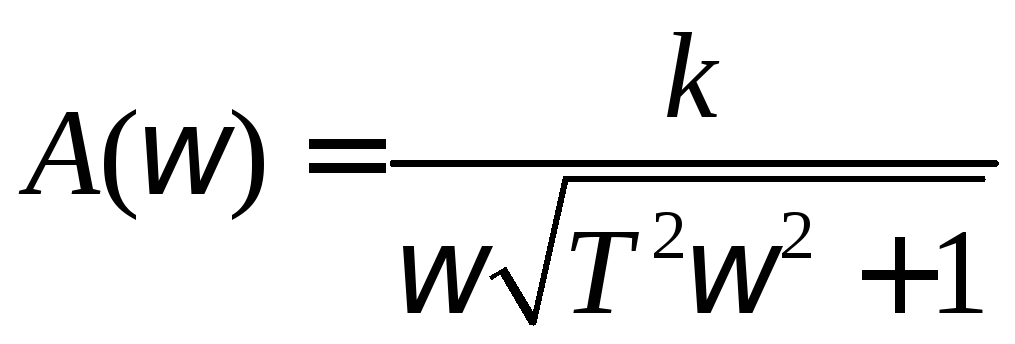 (1.72)
(1.72)
Как и ранее
построение ЛАХ необходимо начинать с
определения сопрягающих частот. Из
выражения (1.72) видно, что сопрягающая
частота здесь одна
![]() .
Далее определяются упрощенные выражения
для построения ЛАХ. Если
.
Далее определяются упрощенные выражения
для построения ЛАХ. Если
![]() ,
то принимается, что
,
то принимается, что![]() и
и![]() .
Если
.
Если![]() ,
то
,
то![]() и
и![]() .
Для частот
.
Для частот![]() ассимптота
ассимптота![]() .
Для частот
.
Для частот![]() асимптота
асимптота![]() .
.
-40
Lw

На рис.1.36 изображена
ЛАХ для интегрирующего звена. Видно,
что характеристика содержит две асимптоты
с отрицательными углами наклона
- 20дб/дек и - 40дб/дек. Для построения
первой асимптоты (на интервале частот
![]() )
необходимо задать
)
необходимо задать![]() и вычислить
и вычислить![]() .
Далее через точку с координатами
.
Далее через точку с координатами![]() и
и![]() до сопрягающей частоты проводится
асимптота с наклоном -20дб/дек. Вторая
асимптота (на интервале частот
до сопрягающей частоты проводится
асимптота с наклоном -20дб/дек. Вторая
асимптота (на интервале частот![]() проводится с отрицательным углом наклона
40дб/дек .
проводится с отрицательным углом наклона
40дб/дек .
Дифференцирующее звено. Выражение для амплитудно-частотной характеристики имеет вид
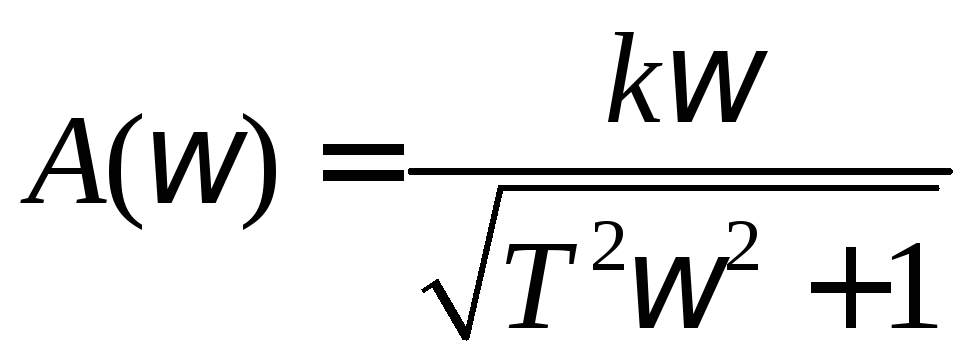 .
(1.73)
.
(1.73)
Сопрягающая частота
![]() .
.
Если
![]() ,
то принимается, что
,
то принимается, что![]() и
и![]() .
Если
.
Если![]() ,
то
,
то![]() ,
,![]() и
и![]() .
.
На рис. 1.36 изображена ЛАХ дифференцирующего звена.
Для построения
первой асимптоты (на интервале частот
![]() )
вычисляют значение
)
вычисляют значение![]() при
при![]() .
Далее через эту точку проводится
асимптота с положительным углом наклона
равным 20дб/дек. Вторая асимптота (на
интервале частот
.
Далее через эту точку проводится
асимптота с положительным углом наклона
равным 20дб/дек. Вторая асимптота (на
интервале частот![]() )
проходит параллельно оси частот.
)
проходит параллельно оси частот.
![]()

5.3. Построение ЛАХ и ЛФХ для сложных передаточных функций
Из предыдущего материала следует, что при построении ЛАХ для различных передаточных функций выполняются одни и те же операции. Опыт построения ЛАХ для сложных передаточных функций позволяет сделать такой же вывод. Поэтому оказалось возможным составить общий порядок построения ЛАХ для передаточных функций вида
 :
(1.74)
:
(1.74)
1. Определение
сопрягающих частот
![]() ;
;
2. Нанесение низкочастотной асимптоты ЛАХ
![]() .
(1.75)
.
(1.75)
Это уравнение
прямой с отрицательным углом наклоном
![]()
![]() ,
где
,
где
![]() порядок астатизма в системе определяется
числом интегрирующих звеньев в регуляторе.
Продолжительность прямой - до первой
сопрягающей частоты
порядок астатизма в системе определяется
числом интегрирующих звеньев в регуляторе.
Продолжительность прямой - до первой
сопрягающей частоты
![]() .
Прямая при частоте
.
Прямая при частоте![]() должна иметь ординату
должна иметь ординату![]() ,
где
,
где![]() коэффициент передачи.
коэффициент передачи.
После каждой из
сопрягающих частот
![]() изменяется наклон характеристики
изменяется наклон характеристики![]() по сравнению с наклоном, который она
имела до рассматриваемой сопрягающей
частоты. Наклон изменяется на – 20 дб/дек
в случае апериодического звена, на –
40 дб/дек – в случае колебательного
звена, +20 дб/дек – в случае дифференцирующего
звена 1 порядка, +40 дб/дек в случае
дифференцирующего звена второго порядка.
по сравнению с наклоном, который она
имела до рассматриваемой сопрягающей
частоты. Наклон изменяется на – 20 дб/дек
в случае апериодического звена, на –
40 дб/дек – в случае колебательного
звена, +20 дб/дек – в случае дифференцирующего
звена 1 порядка, +40 дб/дек в случае
дифференцирующего звена второго порядка.
Пример. Передаточная функция системы имеет вид
 ,
(1.76)
,
(1.76)
где
![]()
![]() ,
,![]() ,
,![]()
![]()
Требуется построить ЛАХ.
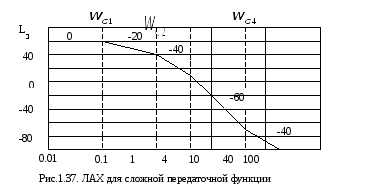
В соответствии с
приведенным выше порядком построение
ЛАХ необходимо начинать с определения
сопрягающих частот. Данные сопрягающих
частот
![]() ,
,![]() ,
,![]() ,
,![]() наносятся на график , рис. 1.37. Далее на
график наносится низкочастотная
асимптота . Передаточная функция (1.76)
относится к системе с астатизмом нулевого
порядка. Это означает, что в уравнении
(1.75) множитель
наносятся на график , рис. 1.37. Далее на
график наносится низкочастотная
асимптота . Передаточная функция (1.76)
относится к системе с астатизмом нулевого
порядка. Это означает, что в уравнении
(1.75) множитель![]() поэтому низкочастотная асимптота
поэтому низкочастотная асимптота![]() представляет собой прямую параллельную
оси частот. Асимптота заканчивается
в точке
представляет собой прямую параллельную
оси частот. Асимптота заканчивается
в точке![]()
![]() .
Сопрягающая частота
.
Сопрягающая частота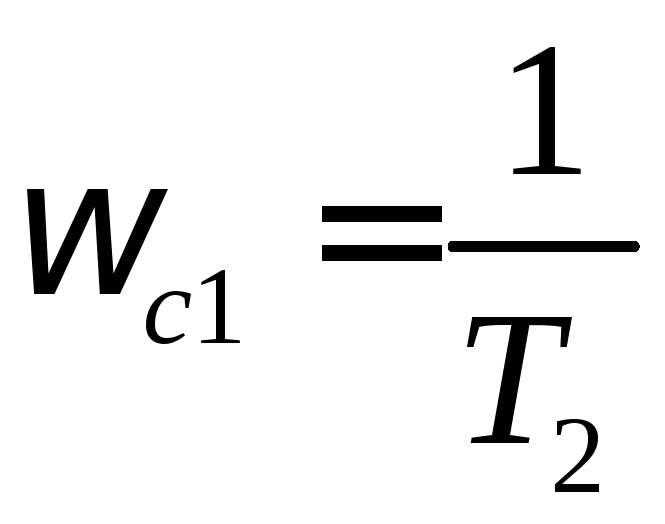 принадлежит
апериодическому звену. Следовательно,
следующая асимптота будет иметь
отрицательный угол наклона равный -20
дб/дек. Асимптота заканчивается в точке
принадлежит
апериодическому звену. Следовательно,
следующая асимптота будет иметь
отрицательный угол наклона равный -20
дб/дек. Асимптота заканчивается в точке![]() .
Сопрягающая частота
.
Сопрягающая частота![]() =
=![]() также принадлежит апериодическому
звену. Поэтому следующая асимптота
будет иметь отрицательный угол наклона
равный уже -40 дб/дек. Этот угол является
результатом суммирования углов наклона
предыдущей и рассматриваемой асимптот.
Асимптота заканчивается в точке
также принадлежит апериодическому
звену. Поэтому следующая асимптота
будет иметь отрицательный угол наклона
равный уже -40 дб/дек. Этот угол является
результатом суммирования углов наклона
предыдущей и рассматриваемой асимптот.
Асимптота заканчивается в точке![]() .
Сопрягающая частота
.
Сопрягающая частота тоже принадлежит апериодическому звену.
Поэтому следующая асимптота будет иметь
угол наклона – 60 дб/дек. Асимптота
заканчивается в точке
тоже принадлежит апериодическому звену.
Поэтому следующая асимптота будет иметь
угол наклона – 60 дб/дек. Асимптота
заканчивается в точке![]() .
Сопрягающая частота
.
Сопрягающая частота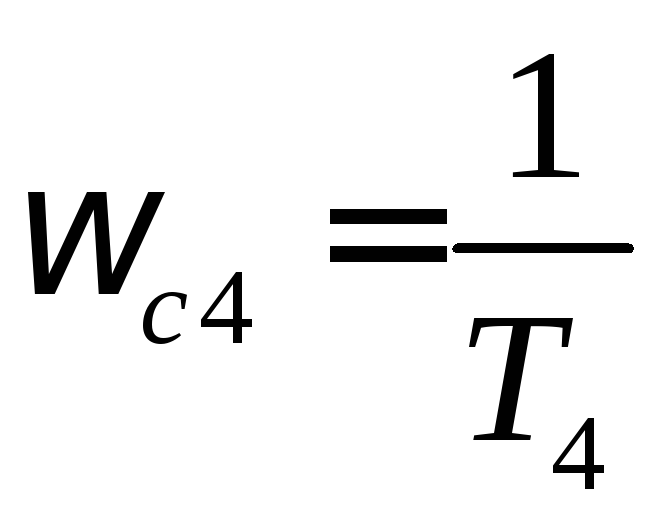 принадлежит дифференцирующему звену,
поэтому угол наклона очередной и
последней асимптоты увеличится на 20
дб/дек и составит – 40 дб/дек.
принадлежит дифференцирующему звену,
поэтому угол наклона очередной и
последней асимптоты увеличится на 20
дб/дек и составит – 40 дб/дек.
Для построения логарифмической фазовой частотной характеристики (ЛФХ) используется та же ось частот, что и для построения ЛАХ. По оси ординат откладывается смещение по фазе в градусах. Однако, принято точку «0» дб. совместить с точкой, где смещение по фазе равно – 1800. При этом отрицательный сдвиг по фазе откладывается по оси ординат вверх, а положительный вниз, рис.1.37,а.
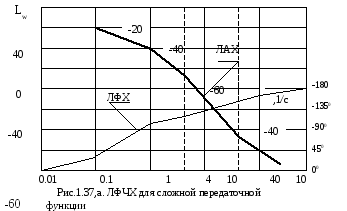
Рассмотрим пример. Пусть требуется построить ЛФХ для системы с передаточной функцией (1.76). Выражение для фазовой частотной характеристики имеет вид
(![]() )
= - arc
tan
10
)
= - arc
tan
10![]() – arc
tan
– arc
tan
![]() – arc
tan
0.005
– arc
tan
0.005![]() + arc
tan
0.25
+ arc
tan
0.25![]() .
(1.77)
.
(1.77)

В таблице 1 представлены результаты расчета слагаемых выражения (1.77) и характеристики в целом на некоторых частотах. Данные таблицы перенесены на график (рис.1.37,а).
Обычно логарифмические амплитудную и фазовую характеристики изображают на одном графике, так как по их взаимному расположению можно определять устойчивость системы. Подробнее эта возможность будет рассмотрена в материале об устойчивости САР.
