Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4628 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Линейная алгебра и аналитическая геометрия

.pdf
Скачиваний:
724
Добавлен:
21.03.2016
Размер:
3.47 Mб
Скачать
☆

В новой системе координат уравнение будет иметь канонический вид: .

Рассмотрим другие кривые 2-го порядка.

3.3.1. Эллипс

Опр. Эллипсом называется кривая 2-го порядка, определяемая в некоторой прямоугольной декартовой системе координат уравнением:

 

 

 

 

 

 

,

.

 

 

 

 

 

 

 

 

Это уравнение называется каноническим уравнением эллипса.

Опр. Равномерным сжатием к оси

называется такое преобра-

зование плоскости, при котором точка

 

переходит в точку

, где

,

 

 

 

.

 

 

Теорема 1. Эллипс может быть получен путем равномерного

сжатия окружности

 

 

 

 

к оси .

 

Доказательство.

Пусть точка

 

лежит на окружности

,

т. е.

 

 

 

 

или

 

. Произведем

равномерное сжатие окружности с коэффициентом

 

 

 

. Тогда

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

После равномерного сжатия точка

 

 

перешла в точку

, координаты которой удовлетворяют уравнению эллипса. Таким образом, точка, лежащая на окружности, при равномерном сжатии переходит в точку, лежащую на эллипсе. Теорема доказана.

Доказанная теорема позволяет представить форму эллипса и построить его (рис. 3.36).

153

Рис. 3.36. Равномерное сжатие окружности к оси

Свойства эллипса:

1. Эллипс симметричен относительно осей координат и относительно начала координат : оси и — оси симметрии; точка — центр симметрии.

2. Эллипс — ограниченная кривая, целиком лежащая в прямоугольнике:

 

 

 

.

Упр. 9. Доказать свойства эллипса.

 

 

Опр. Точки пересечения

эллипса с осями координат

 

 

 

называются вершинами эллип-

са. Отрезок

, а также его длина

называются большой осью;

отрезок

, а также его длина

называются малой осью. Числа и

соответственно называются большой и малой полуосями (рис. 3.37).

Рис. 3.37. Эллипс

154

 

Фокусы эллипса

 

 

 

 

 

 

 

Введем число

.

 

 

Опр. Точки

, лежащие на большой оси эл-

липса, симметрично относительно центра на расстоянии

, называют-

ся фокусами эллипса. Число

называется межфокусным расстоя-

нием.

 

 

 

Для произвольной точки

эллипса отрезки

и

, а

также их длины и называются фокальными радиусами точки . Теорема 2 (бифокальное свойство эллипса). Для любой точки

эллипса сумма расстояний от нее до фокусов есть величина постоянная и равная большой оси эллипса:

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Доказательство.

,

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

аналогично:

 

 

 

 

; тогда

 

 

 

 

 

 

 

. Теорема доказана.

 

 

 

 

 

 

Эксцентриситет эллипса Опр. Эксцентриситетом эллипса называется отношение меж-

фокусного расстояния эллипса к длине его большой оси:

 

или

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Эксцентриситет

эллипса

удовлетворяет

 

неравенствам:

. При

получаем

и

 

; в этом случае эллипс

превращается в окружность с центром в начале координат.

 

 

Форма эллипса зависит от отношения полуосей эллипса

 

. Это

 

 

 

 

 

 

 

 

отношение выражается через эксцентриситет эллипса:

 

 

 

 

.

 

 

 

 

Чем меньше , тем ближе форма эллипса к окружности (

≈ ;

чем ближе к единице, тем ближе число

 

к числу

 

, тем дальше

155

отодвигаются фокусы эллипса друг от друга к концам большой оси, тем более сплющенным оказывается форма эллипса.

Тем самым, эксцентриситет эллипса служит мерой «сплющен-

ности» эллипса.

 

Формулы для фокальных радиусов

и произвольной точки

эллипса, полученные при выводе бифокального свойства эллипса

можно записать в следующем виде:

 

,

.

Директрисы эллипса Опр. Прямые, перпендикулярные к большой оси эллипса и про-

ходящие на расстоянии от центра эллипса, называются директриса-

ми эллипса.

 

 

 

 

 

Уравнения

директрис:

. Директрисы

не пересекают

сам эллипс, они проходят за его пределами, т. к.

 

 

. Обозначения

 

для директрис:

.

 

 

 

 

Рис. 3.38. Фокально-директориальное свойство эллипса

Теорема 3 (фокально-директориальное свойство эллипса, см. рис. 3.38). Для любой точки эллипса отношение расстояния от нее до фокуса эллипса к расстоянию до соответствующей директрисы, есть величина постоянная и равная эксцентриситету эллипса:

156

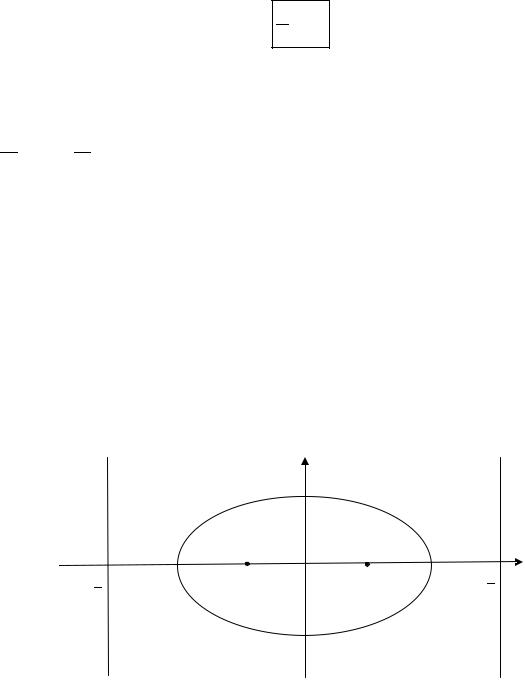
Замечание. Слово «соответствующая» в формулировке теоремы означает, что фокусу соответствует директриса , а фокусу соответствует директриса . Тем самым теорема утверждает, что

и.

Доказательство. Для произвольной точки эллипса расстояния от нее до фокусов (фокальные радиусы) выражаются форму-

лами:

,

. Расстояния от нее до директрис рав-

ны:

,

. Тогда

 

 

 

,

 

 

 

 

 

 

 

 

. Теорема доказана.

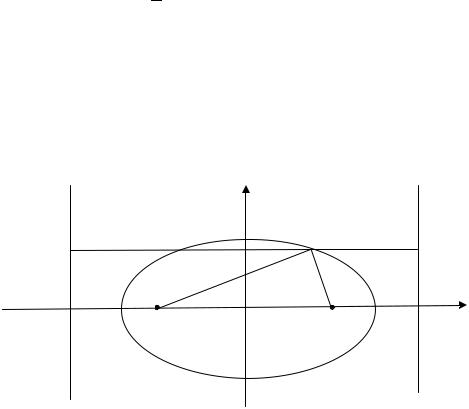
Пример 1. Найти полуоси, вершины, фокусы, эксцентриситет и урав-

нения директрис эллипса, заданного уравнением:

.

Сделать рисунок.

 

Рис. 3.39. К решению примера 1

Приведем уравнение эллипса к каноническому виду:

 

 

 

 

 

 

 

 

. Из канонического уравнения эл-

 

 

 

 

 

липса получим

значения

полуосей:

; тогда

 

 

 

 

 

;

вершины эллипса:

 

 

 

 

 

 

 

 

 

157

; фокусы эллипса:

 

; эксцентриситет

; уравнения директрис

:

 

 

(см.

 

 

рис. 3.39).

Параметрические уравнения эллипса

Каноническое уравнение эллипса можно записать в виде:

 

 

 

 

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

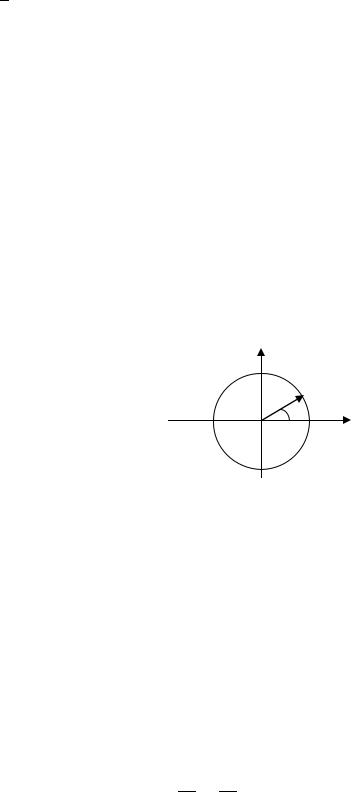
Введем обозначения:

 

,

 

 

 

, тогда

. Это зна-

 

 

 

чит, что точка

с координатами

 

 

 

лежит на единичной окружно-

сти. Введем параметр

— угол

 

поворота вектора

от оси

(см. рис. 3.40). Тогда

 

 

 

 

 

 

 

 

. Следовательно:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

,

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

O

Рис. 3.40. Параметрические уравнения окружности и эллипса

Получаем параметрические уравнения эллипса:

,

.

 

3.3.2. Гипербола

Опр. Гиперболой называется кривая 2-го порядка, определяемая в некоторой прямоугольной декартовой системе координат уравнением:

, .

Это уравнение называется каноническим уравнением гиперболы.

158

Свойства гиперболы:

1. Гипербола симметрична относительно осей координат и относи-

тельно начала координат : оси

и

— оси симметрии; точка

—центр симметрии.

2.Гипербола — неограниченная кривая, целиком лежащая в множестве

Упр. 10. Доказать свойства гиперболы.

Построение гиперболы

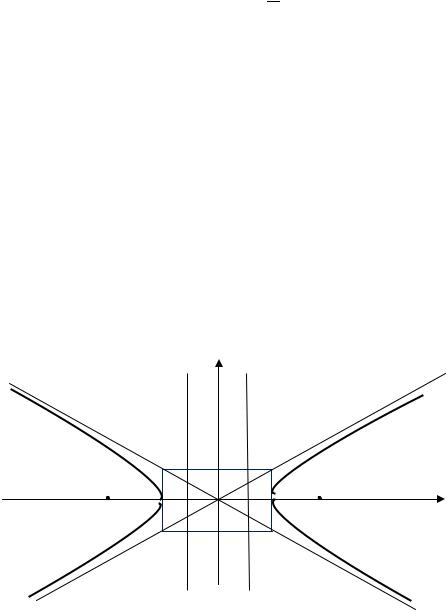
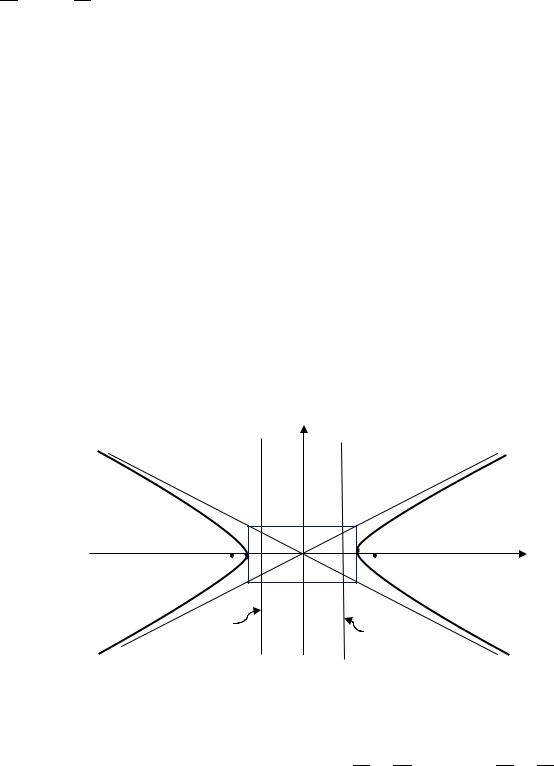
Исследуя каноническое уравнение гиперболы, приходим к выводу, что гипербола состоит из двух бесконечных кривых (ветвей гиперболы), которые можно построить по следующей схеме.

1. Построим прямоугольник со сторонами и с центром в начале координат.

2. Проведем диагонали в этом прямоугольнике и неограниченно продолжим их за пределы прямоугольника. Эти диагонали делят всю плоскость на 4 области. Ветви гиперболы будет лежать в левой и правой областях (рис. 3.41).

Рис. 3.41. Гипербола

159

— для точек левой ветви гиперболы,

3. Построим ветвь гиперболы в правой области так, чтобы кривая касалась прямоугольника с внешней стороны и неограниченно приближалась к продолжениям диагоналей прямоугольника.

Аналогично строим ветвь гиперболы в левой области. При этом кривая должна быть симметрична относительно осей координат.

Прямые, на которых лежат диагонали, называются асимптотами гиперболы. Ветви гиперболы неограниченно приближаются к

асимптотам, при этом не пересекая их.

 

 

Уравнения асимптот:

 

 

.

 

 

 

 

 

Точки касания гиперболы с прямоугольником (точки пересече-

ния гиперболы

с осью

) называются вершинами

гиперболы:

 

. Отрезок

 

, а также его длина

называются

действительной осью гиперболы.

 

 

Отрезок

, где

 

 

, а также его длина

на-

зываются мнимой осью. Это название объясняется тем, что гипербола

не пересекает ось .

 

 

 

 

 

 

Если

, то гипербола называется равносторонней.

 

 

 

 

 

Фокусы гиперболы

 

 

 

Введем число

 

 

 

.

 

 

 

 

 

 

 

 

 

Опр.

Точки

 

 

 

, лежащие на действительной

оси гиперболы, симметрично относительно центра на расстоянии

,

называются фокусами гиперболы.

Число

называется межфокус-

ным расстоянием.

 

 

 

 

 

 

 

Так как

, то фокусы

находятся дальше от центра,

чем вершины гиперболы.

 

 

 

 

 

 

Для произвольной точки

гиперболы отрезки

и

,

а также их длины

и

называются фокальными радиусами точки

.

 

 

 

 

 

 

 

 

Можно доказать (аналогично доказательству теоремы 2), что формулы для фокальных радиусов и произвольной точки гиперболы имеют вид:

,

160

, — для точек правой ветви гиперболы. Из этих формул получаем следующую теорему.

Теорема 4 (бифокальное свойство гиперболы). Для любой точки гиперболы разность расстояний от нее до фокусов по абсолютной

есть величина постоянная и равная действительной оси гиперболы:

 

.

Эксцентриситет гиперболы

Опр. Эксцентриситетом гиперболы

называется отношение

межфокусного расстояния гиперболы к длине его действительной оси:

или

 

.

 

 

 

Из определения следует, что эксцентриситет гиперболы

.

Можно заметить, что чем больше эксцентриситет гиперболы,

тем «более вертикальными» становятся ветви гиперболы, так как при

этом увеличивается угол наклона асимптоты гиперболы.

 

Директрисы гиперболы Опр. Прямые, перпендикулярные к действительной оси гипер-

болы и проходящие на расстоянии

 

от центра гиперболы, называются

 

директрисами гиперболы.

 

 

Уравнения директрис:

 

. Директрисы не пересекают

саму гиперболу, они пересекают действительную ось в точках, кото-

рые находятся ближе к центру, чем вершины гиперболы, т. к.

 

 

.

 

Обозначения для директрис:

.

 

 

 

Теорема 5 (фокально-директориальное свойство гиперболы).

 

Для любой точки гиперболы отношение расстояния от нее до фокуса гиперболы к расстоянию до соответствующей директрисы, есть величина постоянная и равная эксцентриситету гиперболы:

Замечание. Слово «соответствующая» в формулировке теоремы

означает, что фокусу

соответствует директриса , а фокусу

со-

 

 

161

ответствует директриса . Тем самым теорема утверждает, что

и.

Доказательство теоремы аналогично доказательству для случая эллипса.

Пример 1. Найти полуоси, вершины, фокусы, эксцентриситет, уравнения асимптот и директрис гиперболы, заданной уравнением:

. Сделать рисунок.

Приведем уравнение гиперболы к каноническому виду:

 

 

 

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

Из канонического уравнения гиперболы получим значения по-

луосей:

 

 

; тогда

 

 

 

 

; вершины гиперболы:

 

 

 

 

 

 

 

 

 

; фокусы гиперболы:

 

 

 

; эксцен-

триситет

 

 

; уравнения асимптот:

 

 

 

; уравнения ди-

 

 

 

 

ректрис

:

 

 

 

 

(см. рис. 3.42).

-

Рис. 3.42. К решению примера 1

Сопряженная гипербола

Кривая, определяемая уравнением:

называется сопряженной гиперболой по отношению к основной гиперболе (рис. 3.43).

162

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности