§ 4. Ортогональность функций Бесселя.

Теорема (без доказательства). Функции Бесселя являются ортогональными (для всех ν > – 1) с весом ρ(х)=х, т.е.

. (19)

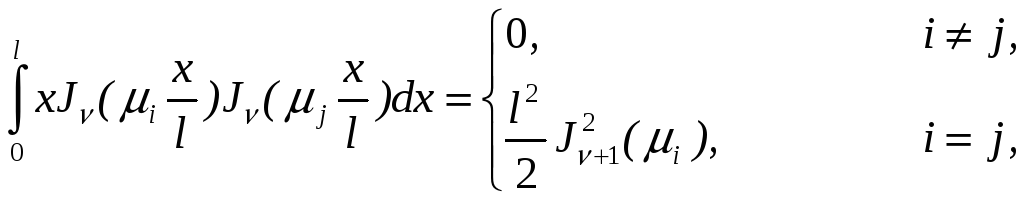(21)

где – корень уравнения . Для задачи о колебании мембраны

§ 5. Разложение произвольной функции в ряд по функциям Бесселя.

Произвольная функция может быть разложена в ряд по функциям Бесселя следующим образом:

. (22)

Умножим обе части на и проинтегрируем от 0 до l. Тогда в правой части из всего ряда только один член окажется не нулевым, а именно при .

(23)

Вопрос о разложении любой функции в ряд по ортогональным функциям Бесселя является актуальным. При решении многих задач математической физики можно произвольную функцию разложить в ряд по функциям Бесселя. Зная, что для каждой из функций Бесселя эта задача решается, можно получить общее решение исходной задачи, суммируя все решения, полученные для функций Бесселя.

Это используется при численном решении задач математической физики.

§ 6. Общее решение задачи о колебании круглой мембраны

Вернемся к задаче о колебании круглой мембраны. С учетом того, что мы получили бесконечный набор значений λ_nm , полученные нами уравнения после применения метода разделения переменных следует переписать в следующем виде

(24)

(25)

(26)

Решения этих уравнений соответственно будут иметь вид (после переобозначения произвольных констант)

(27)

(28)

(29)

И тогда можем записать

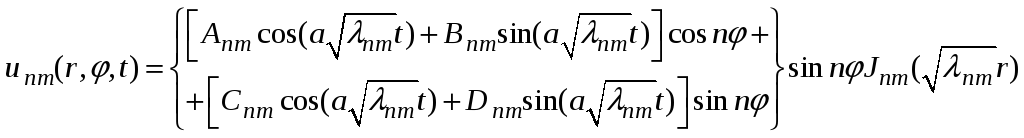(30)

Здесь следует обратить внимание на то, константа стала не нужна. Следовательно, и вопрос об определении функции J_nm через неопределенный коэффициент a₀ снимается с повестки дня. Общее решение уравнения колебания мембраны запишется как

(31)

Для определения остальных констант воспользуемся начальными условиями

(32)

и ортогональностью функций Бесселя.

Подставив в общее решение , получим

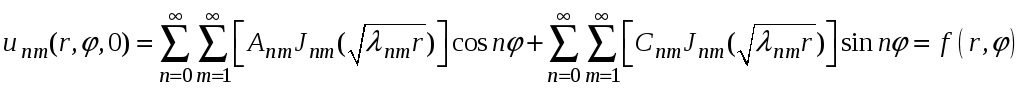(33)

Этот ряд представляет собой разложение периодической функции в ряд Фурье на интервале (0, 2π) и, следовательно, выражения в квадратных скобках должны быть коэффициентами рядя Фурье, а именно

(34)

(35)

С другой стороны эти формулы представляют разложение функций в правых частях по функциям Бесселя. Тогда

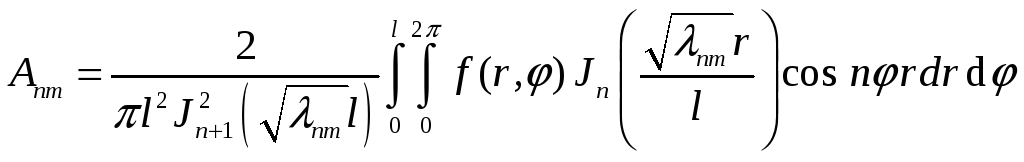(36)

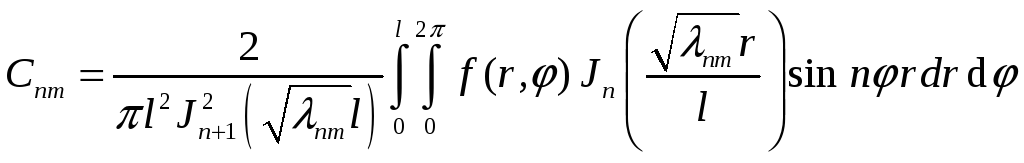(37)

Аналогичным образом определяются и коэффициенты B_nm и D_nm после записи второго начального условия и подстановки в него производной по времени от общего решения. В результате в формуле (33) функция заменится на , коэффициенты А_nm и С_nm заменятся на B_nm и D_nm, а перед знаками суммирования появится множитель .