
- •Санкт-Петербургский национальный исследовательский университет
- •Введение
- •Часть 1. Надежность технических систем
- •Вероятностная оценка надежности технической системы
- •Экспоненциальный закон надежности
- •Системы, резервированные по методу голосования
- •Резервированные системы с параллельным включением резервных элементов
- •Вопросы
- •Простейший поток событий и марковские модели функционирования технической системы
- •Потоки событий. Простейший поток и его свойства
- •Аппроксимация потока редких событий пуассоновским потоком
- •Марковские модели функционирования технической системы
- •Непрерывные цепи Маркова
- •Резервированные системы с восстановлением. Уравнения Колмогорова
- •Вопросы
- •Аппаратурная и информационная надежность навигационной системы
- •Часть 2. Техническая диагностика
- •Основные принципы проектирования средств диагностирования
- •Назначение и достоверность средств диагностирования
- •Математические модели объектов диагностирования
- •Модели безынерционных преобразователей
- •Динамические модели
- •Логико-динамические модели мультирежимных систем
- •Иерархический подход к проектированию и организации средств диагностирования
- •Организация диагностирования. Безусловные и условные диагностические эксперименты
- •Диагностические экспертные системы
- •Структура средств диагностирования навигационной системы
- •Вопросы
- •Методы тестового диагностирования
- •Тестовое диагностирование безынерционных преобразователей
- •Тестовое диагностирование динамических устройств
- •Тестовое диагностирование дискретных устройств. Общий подход
- •Тестовое диагностирование линейных дискретных устройств. Структурный подход
- •Тестовое диагностирование линейных дискретных устройств. Абстрактный подход
- •Тестовое диагностирование аналоговых линейных устройств
- •Тестовое диагностирование мультирежимных систем
- •Принципы тестового диагностирования мультирежимных систем
- •Тестовое диагностирование процессора
- •Тестовое диагностирование распределенных информационно-управляющих систем
- •Структура средств диагностирования
- •Построение проверяющего теста. Управляемость и наблюдаемость периодически нестационарной системы
- •Синтез модели системы обмена
- •Методы функционального диагностирования
- •Методы функционального диагностирования для обнаружения отказов
- •Функциональное диагностирование при поиске структурных нарушений
- •Функциональное диагностирование при поиске отказов в пространстве сигналов
- •Функциональное диагностирование при поиске отказов в пространстве параметров
- •Функциональное диагностирование информационных отказов в интегрированной навигационной системе
- •Вопросы
- •Приложение 1. Основные понятия теории вероятностей
- •Приложение 2. Модели представления знаний.
- •Приложение 3. Основы нечеткого анализа
- •Литература
Тестовое диагностирование динамических устройств
Тестовое диагностирование дискретных устройств. Общий подход
Ситуация
существенным образом осложняется, если
объект представляет собой динамическую
систему. В том случае он имеет следующую
структуру (рис. 4.7), включающую два
безынерционных функциональных
преобразователя
![]() и
и![]() ,
а также инерционный блок (интеграторы,
задержки, триггеры). Если попытаться
следовать букве иерархического подхода,
то средства диагностирования для
динамического устройства нужно было
бы представить как состоящие из двух
частей: теста для безынерционных
преобразователей и теста для связей
между ними, реализуемых через инерционные
элементы. Однако реализовать на практике
такое предложение, как правило, будет
затруднительно, т.к. входные векторы
этих преобразователей имеют в своем
составе не только независимые входы
,
а также инерционный блок (интеграторы,
задержки, триггеры). Если попытаться
следовать букве иерархического подхода,
то средства диагностирования для
динамического устройства нужно было
бы представить как состоящие из двух
частей: теста для безынерционных
преобразователей и теста для связей
между ними, реализуемых через инерционные
элементы. Однако реализовать на практике
такое предложение, как правило, будет
затруднительно, т.к. входные векторы
этих преобразователей имеют в своем
составе не только независимые входы![]() ,
на которых можно формировать любые
входные сигналы, но также сигналы
обратных связей, значения которых
определяются внутренним состоянием
объекта
,
на которых можно формировать любые
входные сигналы, но также сигналы
обратных связей, значения которых
определяются внутренним состоянием
объекта![]() .
В результате процесс формирования
требуемых тестовых наборов
.
В результате процесс формирования
требуемых тестовых наборов![]() на входе безынерционных преобразователей
превращается в многошаговую процедуру
(рис. 5.2), порождающую определенную
тестовую последовательность. Начальный
отрезок этой последовательности
устанавливает объект из начального
состояния
на входе безынерционных преобразователей
превращается в многошаговую процедуру
(рис. 5.2), порождающую определенную
тестовую последовательность. Начальный
отрезок этой последовательности
устанавливает объект из начального
состояния![]() в тестовое состояние
в тестовое состояние![]() .
В этом состоянии на вход объекта подается
входной сигнал
.
В этом состоянии на вход объекта подается
входной сигнал![]() ,
а затем полученная реакция устройства
в виде его состояния
,
а затем полученная реакция устройства
в виде его состояния![]() транслируется на выход объекта путем
организации соответствующего
чувствительного пут
транслируется на выход объекта путем
организации соответствующего
чувствительного пут и.
В результате значение выхода
и.
В результате значение выхода![]() объекта будет зависеть от результатов
проверки
объекта будет зависеть от результатов
проверки![]() .
Проверка связей между безынерционными
преобразователями через инерционные
элементы составляет второй этап
диагностирования, который обычно
выполняется попутно с первым.
.
Проверка связей между безынерционными
преобразователями через инерционные
элементы составляет второй этап
диагностирования, который обычно
выполняется попутно с первым.
Пусть
тест для безынерционных преобразователей
устройства известен и задан двумя
множествами для φ –
![]() и для δ –
и для δ –![]() ,
где каждый тестовый входной вектор из
множеств
,
где каждый тестовый входной вектор из
множеств![]() и
и![]() состоит из подвектора внешних входов
и подвектора внутреннего состояния,
т.е.
состоит из подвектора внешних входов
и подвектора внутреннего состояния,
т.е.![]() и требует для своей реализации процедур
установки и трансляции. Тогда тестовая
входная последовательность для устройства
имеет следующую структуру
и требует для своей реализации процедур
установки и трансляции. Тогда тестовая
входная последовательность для устройства
имеет следующую структуру
 .
.
где последний элемент последовательности предназначен для проверки элементов задержки, которая по существу тривиальна и обычно выполняется попутно с проверкой преобразователей.
Нетрудно видеть, что описанная процедура построения теста достаточно сложна, особенно если учесть, что установку и трансляцию придется осуществлять в условиях присутствия отказа. Нетрудно, по-видимому, догадаться, что стремление построить «честный» тест на этом пути приведет нас к весьма продолжительным, а возможно, и недопустимо продолжительным с точки зрения практики проверкам. Конечно, в этом случае будет правильным потребовать от разработчика устройства предусмотреть возможность его установки, если не в любое тестовое, то хотя бы в одно начальное состояние.
Тестовое диагностирование линейных дискретных устройств. Структурный подход
Проблема существенно упрощается в случае линейных устройств, поэтому проиллюстрируем описанные идеи на примере тестового диагностирования устройства из этого класса [15]:
![]() (5.1)
(5.1)
где элементы векторов и матриц принимают значения из множества {0, 1}, т.е. устройство является линейным в поле вычетов по модулю 2 (операция сложения – исключающее ИЛИ).
Установочная последовательность и управляемость устройства
Пусть
тест для безынерционных преобразователей
φ и δ (рис. 4.8) рассматриваемого устройства
представлен двумя соответствующими
множествами входных векторов для φ –
![]() и для δ –
и для δ –![]() .
В линейном устройстве преобразователь
φ описывается матрицамиF
и G,
а преобразователь δ матрицей H.
Как говорилось выше, каждый тестовый
входной вектор из множеств
.
В линейном устройстве преобразователь
φ описывается матрицамиF
и G,
а преобразователь δ матрицей H.
Как говорилось выше, каждый тестовый
входной вектор из множеств
![]() и
и![]() состоит из подвектора внешних входовu
и подвектора внутреннего состояния x
и требует для своей реализации процедур
установки и трансляции.
состоит из подвектора внешних входовu
и подвектора внутреннего состояния x
и требует для своей реализации процедур
установки и трансляции.
Рассмотрим
процедуру установки устройства в
некоторое заданное тестовое состояние
![]() .
Запишем выражения для состояния системы
на протяжении изn
тактов:
.
Запишем выражения для состояния системы
на протяжении изn
тактов:
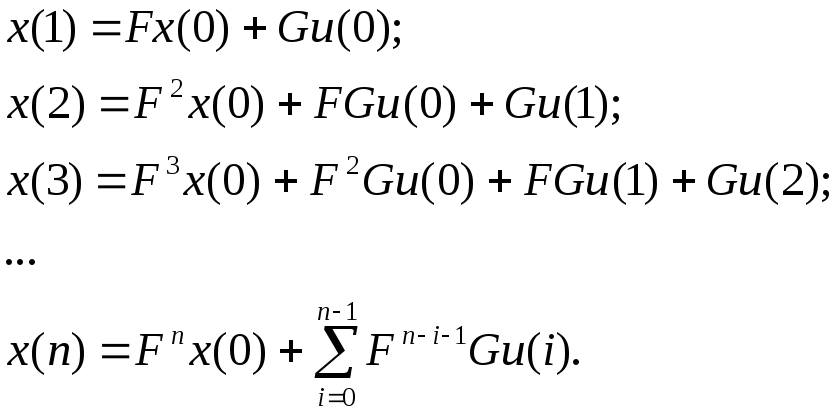
Используя блочные матрицы, перепишем последнее выражение для финального состояния, в которое переходит устройство под действием установочной последовательности (u(0), u(1),…, u(n-1)):

Введем
матрицу![]() ,
известную как матрица управляемости,
и матрицу-столбец входной последовательностиu*:
,
известную как матрица управляемости,
и матрицу-столбец входной последовательностиu*:
![]() (5.2)
(5.2)
Отсюда
в предположении, что ![]() ,получаем выражение
для вычисления установочной
последовательности:
,получаем выражение
для вычисления установочной
последовательности:
![]() . (5.3)
. (5.3)
где верхний индекс «+» означает обращение матрицы, если она квадратная, и псевдообращение матрицы, если она прямоугольная [17].
Таким
образом, если матрица управляемости
неособенна (критерий
управляемости),
то с использованием выражений (5.3) для
любого состояния
![]() может быть вычислена установочная
последовательность длинойn.
В таких случаях говорят, что устройство
полностью управляемо. При этом общее
определение управляемости звучит
следующим образом.
может быть вычислена установочная
последовательность длинойn.
В таких случаях говорят, что устройство
полностью управляемо. При этом общее
определение управляемости звучит
следующим образом.
Устройство
управляемо, если для каждого момента
времени t0
найдется такой момент времени t1
(![]() )
такой, что для любой пары состояний (
)
такой, что для любой пары состояний (![]() )
существует входная последовательность,
переводящая систему из
)
существует входная последовательность,
переводящая систему из
![]() в
в![]() .
.
Следует иметь в виду, что для конкретного управляемого устройства установочные последовательности могут иметь длину, меньшую n. Это происходит в тех случаях, когда входы устройства непосредственно связаны со входами многих элементов задержки (интеграторов). Причем когда длина установочной последовательности оказывается равнойk<n, то говорят оk- управляемости (k– индекс управляемости).
Транслирующая последовательность и наблюдаемость устройства
Теперь рассмотрим процесс трансляции на выход результатов неправильного срабатывания устройства на тестовом наборе. Эти результаты выражены неправильным вектором состояния, поэтому задача сводится к оценки значения этого вектора. Запишем выражения для выхода устройства на протяжении n тактов:
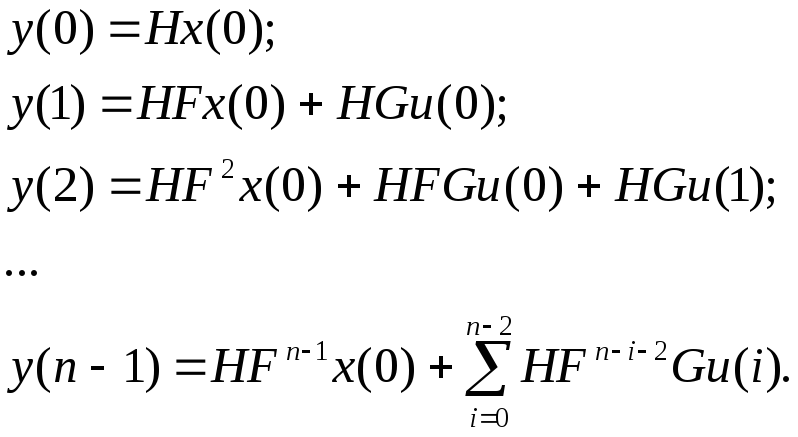
Преобразуем полученные выражения, перенеся в каждом из них слагаемые, содержащие u, в левую часть:
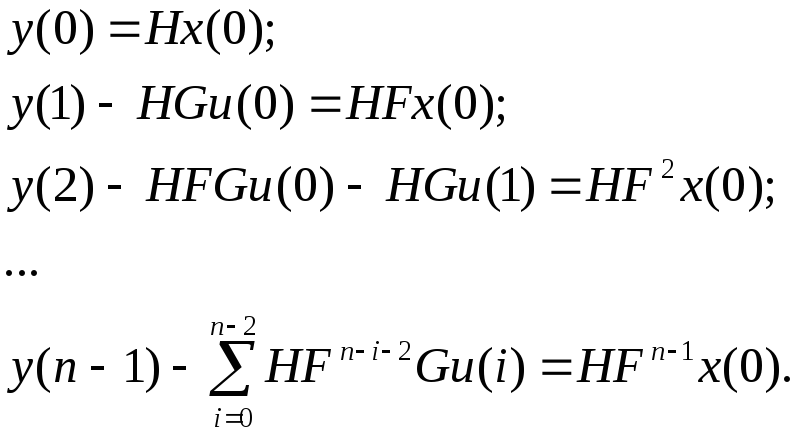
Обозначим
вектор левых частей через
![]() и введем матрицу наблюдаемости
и введем матрицу наблюдаемости![]() .
В результате получаем
.
В результате получаем
![]() . (5.4)
. (5.4)
Если
матрица
![]() неособенная, то
неособенная, то
![]() , (5.5)
, (5.5)
Таким
образом, если матрица
![]() неособенная, то состояние
неособенная, то состояние![]() всегда может быть определено (критерий
наблюдаемости). В случае, когда критерий
выполняется, говорят, что система
полностью наблюдаема.
всегда может быть определено (критерий
наблюдаемости). В случае, когда критерий
выполняется, говорят, что система
полностью наблюдаема.
Обращаем внимание на тот факт, что для наблюдаемой системы любая входная последовательность длины nявляется транслирующей.
Также как и при определении установочных последовательностей для конкретного наблюдаемого устройства транслирующие последовательности могут иметь длину, меньшую n. Это происходит в тех случаях, когда выходы устройства непосредственно связаны с выходами многих элементов задержки (интеграторов). Причем когда длина транслирующей последовательности оказывается равнойk<n, то говорят оk-наблюдаемости (k– индекс наблюдаемости).
Для того, чтобы проникнуться в физический смысл свойства наблюдаемости, ниже приводятся примеры трех динамических систем четвертого порядка с двухмерным входным вектором, одна из которых наблюдаема, а две ненаблюдаемы.
Пример 5.1.(наблюдаемая система). Проверим наблюдаемость системы, которая характеризуется матрицами:
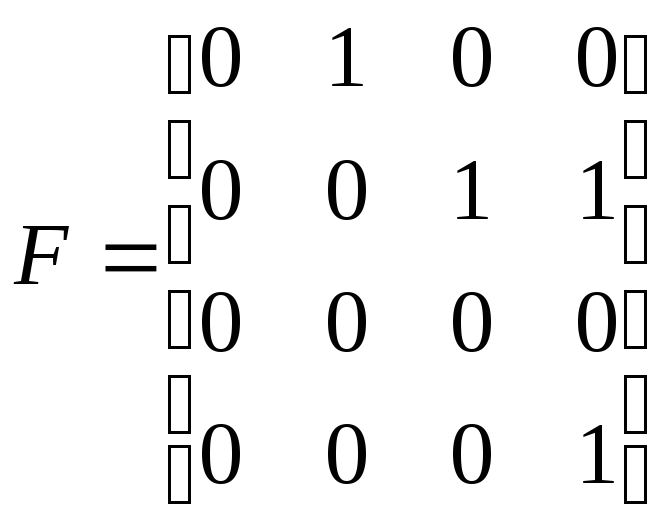 ;
;![]() ;
;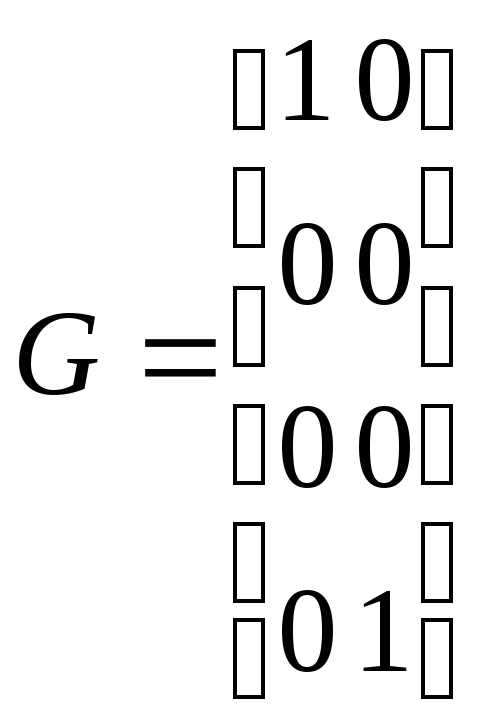 .
.
Определим матрицу наблюдаемости:
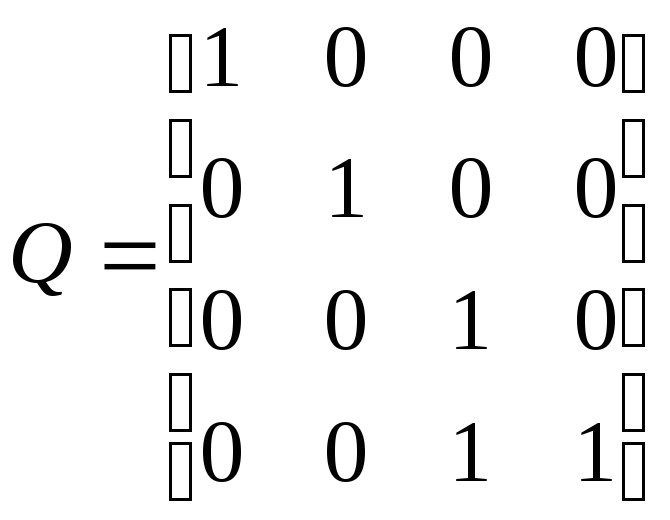 .
.
Определитель
этой матрицы не равен нулю, т.е. матрица
неособенная. Следовательно, система
наблюдаема. Структурная схема системы
приведена на рис. 5.3а, где прямоугольники
обозначают элементы задержки, кружки
– сумматоры;![]() – вектор состояния;
– вектор состояния;![]() – вектор возмущений, z – измерения
(скалярный выход).
– вектор возмущений, z – измерения
(скалярный выход).

Пример 5.2.(ненаблюдаемая система).Проверить наблюдаемость системы, которая характеризуется матрицами:
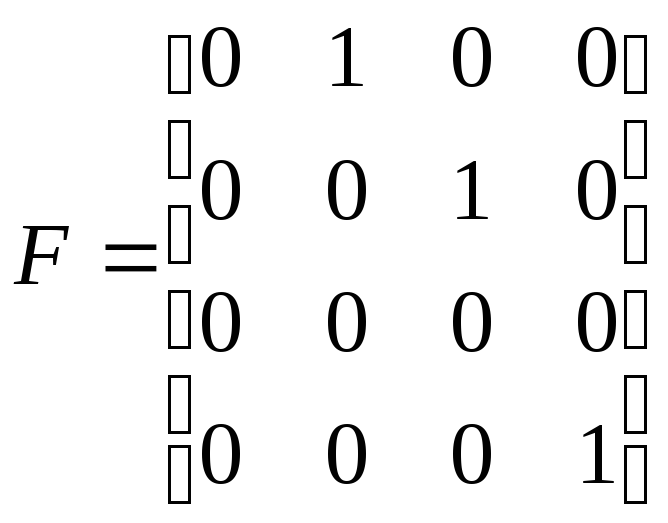 ,
,![]() ,
,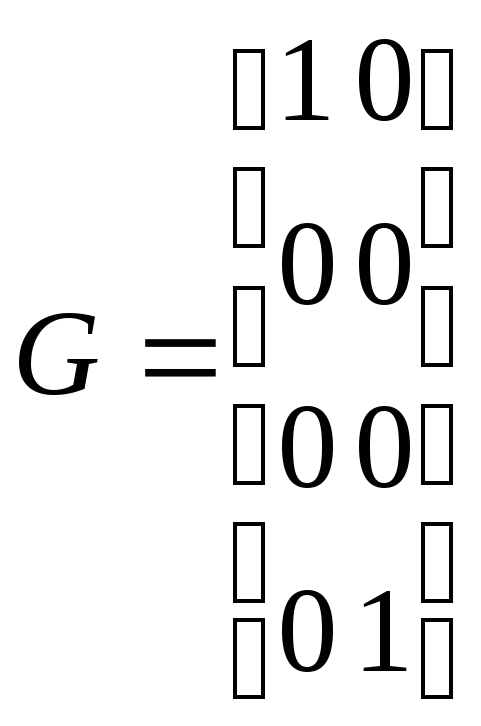 .
.
Определим матрицу наблюдаемости:
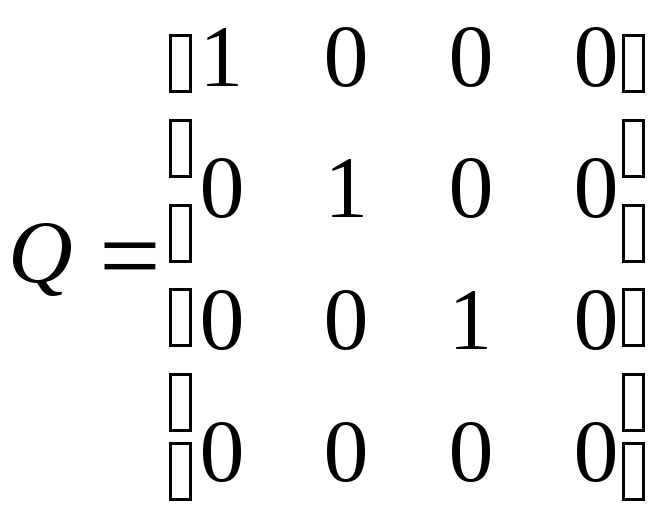 .
.
Определитель этой матрицы равен нулю, т.е. матрица особенная. Следовательно, система ненаблюдаема. Структурная схема системы приведена на рис. 5.3б. Из ее анализа легко заметить причину ненаблюдаемости системы. Действительно, сигнал с четвертого элемента задержки не участвует в формировании выхода системы, а значит, его состояние не может быть оценено по измерениям.
Пример 5.3. (ненаблюдаемая система).Проверить наблюдаемость системы, которая характеризуется матрицами:
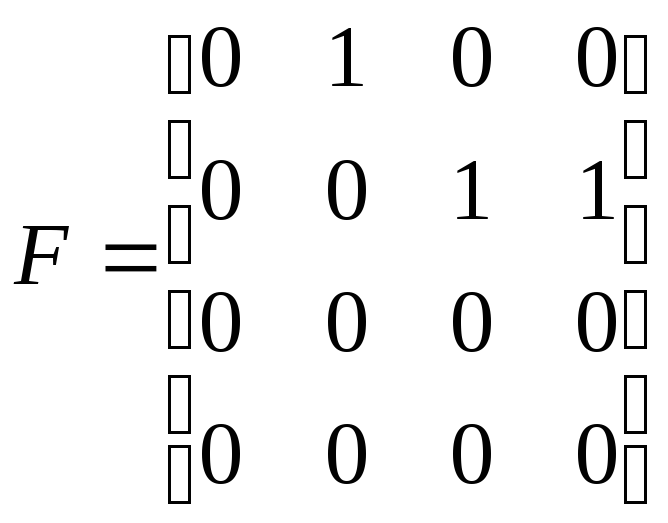 ;
;![]() ;
;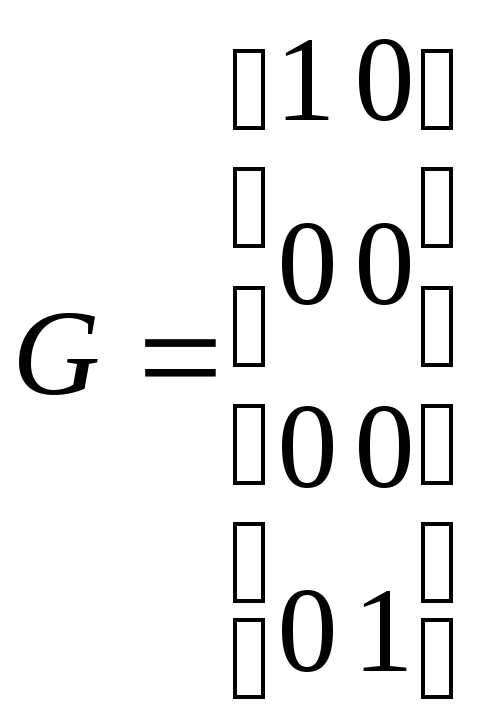 .
.
Определим матрицу наблюдаемости
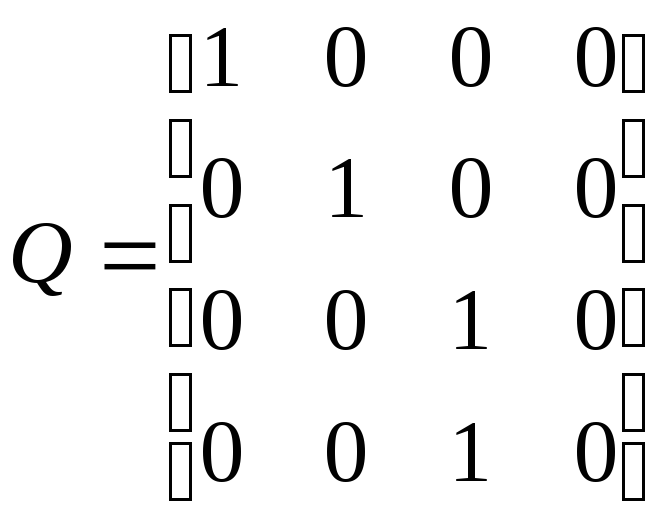 .
.
Определитель этой матрицы также равен нулю, т.е. матрица особенная. Следовательно, система также ненаблюдаема. Структурная схема системы приведена на рис. 5.3 в. Из ее анализа ненаблюдаемость системы следует не с такой очевидностью, как в предыдущем случае, однако ее также можно заметить. Действительно, четвертый и третий элементы задержки, хотя и участвуют в формировании выхода системы, но представлены при этом суммой своих значений. В результате по измерениям невозможно определить, какой вклад в эту сумму вносит каждое из слагаемых, а значит, и невозможно оценить состояние системы.
Последний пример является достаточно значимым с точки зрения практики. Заметим, что в этом примере при различной динамике фрагментов, выходы которых суммируются, система становится наблюдаемой. Действительно, в рассмотренном примере матрицы динамики фрагментов, выходы которых суммируются, одинаковы и равны нулю (состояние третьего и четвертого элементов задержки не зависят от состояний каких-либо элементов задержки). Однако если матрицу динамики в одном из фрагментов изменить, то система становится наблюдаемой. Этот эффект можно заметить при переходе от третьего примера к первому. В первом примере также суммируются выходы третьего и четвертого элементов задержки, но матрица динамики, включающая четвертый элемент задержки равна единице, а не нулю, как это имеет место во фрагменте с третьим элементом задержки. В результате, как уже отмечалось, система из первого примера наблюдаема.
Не будем приводить подобных примеров для обсуждения свойства управляемости, поскольку придем к похожим выводам. Об этом можно уверенно говорить, основываясь на известном принципе двойственности.
Из всего сказанного можно сделать один очень важный вывод: в линейном устройстве задачи установки и трансляции могут решаться в предположении, что система исправна, поскольку любое отклонение от неправильного функционирования будет обнаружено на одном из последующих nтактов.
Пример 5.1. Построить тест, обнаруживающий одиночные константные отказы в линейном двоичном устройстве, которое является 3-наблюдаемым и 3-управляемым и описывается матрицами:
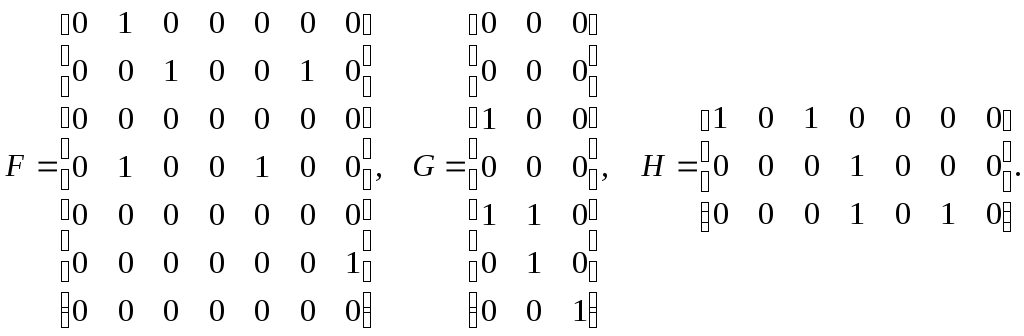
Это
устройство является 3-управляемым и
3-наблюдаемым, поскольку как матрица
![]() ,
так и матрица
,
так и матрица![]() содержат по 7 линейно независимых
столбцов. Эти столбцы образуют матрицы
содержат по 7 линейно независимых
столбцов. Эти столбцы образуют матрицы

Тест
для преобразователей
![]() и
и![]() задан и приведен в таблице 5.1.
задан и приведен в таблице 5.1.
Таблица 5.1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 1 0 1 |
0 0 1 1 |
0 0 1 1 |
0 0 1 1 |
0 1 0 1 |
0 1 0 1 |
0 0 1 1 |
0 0 1 1 |
0 1 0 1 |
0 0 0 1 |
В
соответствии с таблицей первый тестовый
переход совершается из нулевого
состояния, в которое, как предполагается,
устройство устанавливается перед
началом работы специальным сигналом.
Поэтому необходимо установить устройство
последовательно в состояния
![]() и
и![]() ,
подавая в каждом из них на вход устройства
соответствующий тестовый входной набор
(010, 100, 111). С использование выражения
(5.3) вычислим для каждого из трех тестовых
состояний одну из возможных установочных
последовательностей:
,
подавая в каждом из них на вход устройства
соответствующий тестовый входной набор
(010, 100, 111). С использование выражения
(5.3) вычислим для каждого из трех тестовых
состояний одну из возможных установочных
последовательностей:
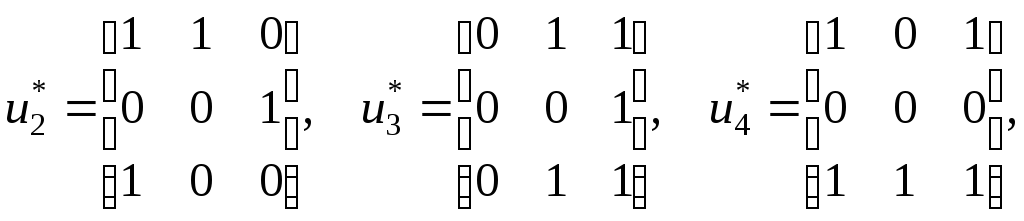
В результате длина итоговой тестовой последовательности равна 16, а сама последовательность имеет вид:
 .
.
Последние три нулевых вектора предназначены для трансляции на выход результатов последнего тестового перехода.
