
лекция 4
.docxМинистерство образования и науки РФ
ФГБОУ ВПО «Кубанский государственный технологический
университет»
Кафедра электротехники и электрических машин
|
УТВЕРЖДАЮ |
||
|
Заведующий кафедрой электротехники и электрических машин
|
||
|
к.т.н., доцент |
|
ЯЯ.М. Кашин
|
|
____ _______ 2015 г.
|
||
Конспект лекций
по дисциплине «Численные методы расчета
электрооборудования»
для студентов направления 13.04.02 «Электроэнергетика и электротехника»
Квалификация выпускника – магистр
Разработал:
к.т.н., доц. И.Н. Автайкин
Обсужден на заседании кафедры
электротехники и электрических машин
25 августа 2015 г. (протокол № 1)
Секретарь кафедры
к.т.н., доц. С.А. Попов
2015 г.
Лекция № 1 (2 часа)
по дисциплине «Численные методы расчета электрооборудования»
Тема № 4. Численное дифференцирование
Цели: 1. Формирование следующих компетенций:
ПКД-3 Способностью к освоению и применению современных средств анализа и моделирования работы электрооборудования
2. Формирование уровня обученности:
Знать: современных средств анализа и моделирования работы электрооборудования.
Уметь: применять современные методы решения математических задач с использованием компьютерной техники.
Владеть: современным математическим аппаратом позволяющим анализировать математические модели электрооборудования.
Материальное обеспечение:
Учебные вопросы
1. Метод Эйлера;
2. Усовершенствованный метод Эйлера;
3. Модифицированный метод Эйлера;
4. Метод Рунге-Кута.
Литература
1. Бахвалов Н.С., Жидков Н.П. Кобельков Г.М. Численные методы / Учебн. пособие- М.: Наука, 2011.- 631с.
2. Марчук Г.И. Методы вычислительной математики / Учебн. пособие- М.: Наука, 2011.- 535с.
Методы решения однородных дифференциальных уравнений.
Дифференциальным называется уравнение, содержащее один или несколько производных. В зависимости от количества не зависимых переменных, дифференциальные уравнения делятся на две категории.
-
Обыкновенные дифференциальные уравнения (ОДУ)
-
Дифференциальные уравнения в частных производных.
Обыкновенными дифференциальными
уравнениями называются такие уравнения,
которые содержат одну или несколько
производных от искомой функции
 .
Их можно записать виде
.
Их можно записать виде
 (1)
(1)
 независимая
переменная
независимая
переменная
Наивысший порядок
 ,
входящий в уравнение (1) называется
порядком дифференциального уравнения.
,
входящий в уравнение (1) называется
порядком дифференциального уравнения.
Простейшим (линейным) ОДУ является уравнение (1) разрешенное относительно производной
 (2)
(2)
Решением дифференциального
уравнения (1) называется всякая функция,
 которая после ее подстановки в уравнение
обращает его в тождество.
которая после ее подстановки в уравнение
обращает его в тождество.
Основная задача, связанная
с линейной ОДУ известно как задача Каши:
найти решение уравнения (2) в виде функции
 удовлетворяющий начальному условию
удовлетворяющий начальному условию
 (3)
(3)
Геометрически это означает,
что требуется найти интегральную кривую,
 проходящую через точку
проходящую через точку
 )
при выполнение равенства (2).
)
при выполнение равенства (2).
Численный с точки зрения
задачи Каши означает: требуется построить
таблицу значений функции
 удовлетворяющий уравнение (2) и начальное
условие (3) на отрезке
удовлетворяющий уравнение (2) и начальное
условие (3) на отрезке
 с некоторым шагом
с некоторым шагом
 .
Обычно считается, что
.
Обычно считается, что
 то есть начальное условие задано в левом
конце отрезка.
то есть начальное условие задано в левом
конце отрезка.
1. Метод Эйлера.
Простейшим из численных методов решения дифференциального уравнения является метод Эйлера. В его основе лежит идея графического построения решения дифференциального уравнения, однако этот метод дает одновременно и способ нахождения искомой функции в численной форме или таблицы.
Пусть дано уравнение
 с начальным условием
с начальным условием
 то есть поставлена задача Каши. Решим
вначале следующую задачу. Найти простейшим
способом приближенное значение решения
в некоторой точке
то есть поставлена задача Каши. Решим
вначале следующую задачу. Найти простейшим
способом приближенное значение решения
в некоторой точке
 где
где
 -достаточно
малый шаг. Уравнение (2) совместно с
начальным условием (3) задают направление
касательной искомой интегральной кривой
в точке
-достаточно
малый шаг. Уравнение (2) совместно с
начальным условием (3) задают направление
касательной искомой интегральной кривой
в точке
 с координатами
с координатами

Уравнение касательной имеет вид

Двигаясь вдоль этой
касательной, получим приближенное
значение решения в точке
 :
:

или
 (4)
(4)
Располагая приближенным
решением в точке
 можно повторить описанную ранее
процедуру: построить прямую проходящую
через эту точку с угловым коэффициентом
можно повторить описанную ранее
процедуру: построить прямую проходящую
через эту точку с угловым коэффициентом
 ,
и по ней найти приближенное значение
решения в точке
,
и по ней найти приближенное значение
решения в точке
 .
.
Заметим, что эта прямая не
является касательной к реальной
интегральной кривой, поскольку точка
 нам не доступна, однако если
нам не доступна, однако если
 достаточно
мало то получаемые приближенные будут
близки к точным значениям решения.
достаточно
мало то получаемые приближенные будут
близки к точным значениям решения.
Продолжая эту идею, построим систему равно отстоящих точек
 .
.
Получение таблицы значений
искомой функции
 по методу Эйлера заключается в циклическом
применение формулы
по методу Эйлера заключается в циклическом
применение формулы
 (5)
(5)

Рисунок. 1. Геометрическая иллюстрация метода Эйлера
Решение ОДУ в некоторой точке xi называется устойчивым, если найденное в этой точке значение функции yi мало изменяется при уменьшении шага интегрирования. Для проверки устойчивости, таким образом, надо провести два расчета значения (yi) – с шагом интегрирования 2h и при уменьшенной (например, двое) величине шага. В качестве критерия устойчивости можно использовать малость относительного изменения полученного решения при уменьшении шага интегрирования

где
 - решение, рассчитанное с шагом 2h ,
- решение, рассчитанное с шагом 2h ,
 – решение, рассчитанное с
– решение, рассчитанное с
шагом h .
Пример
В качестве примера проведем расчеты по формулам метода Эйлера с
шагом h=0,05 и h=0,1 для задачи
Коши
 .
.
Формулы для расчета имеют
вид



Рассчитываем с шагом h = 0.1
0.

1.

2.

3.

***
10.

2. Усовершенствованный метод Эйлера
Точность метода Эйлера можно повысить, если воспользоваться для аппроксимации интеграла более точной формулой интегрирования –формулой трапеций.
Основная идея этого метода:
вычисляемое по формуле (5) очередное
значение
 будет точнее, если значение производной,
то есть угловой коэффициент прямой
замещающей интегральную кривую на
отрезке
будет точнее, если значение производной,
то есть угловой коэффициент прямой
замещающей интегральную кривую на
отрезке
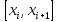 будет вычисляться не по левому краю (то
есть в точке
будет вычисляться не по левому краю (то
есть в точке
 ),
а по центру отрезка
),
а по центру отрезка
 .
Но так как значение производной между
точками
.
Но так как значение производной между
точками
 не вычисляется, то перейдем к сдвоенным
участкам
не вычисляется, то перейдем к сдвоенным
участкам
 центром, в которых является точка
центром, в которых является точка
 ,
при этом уравнение прямой получает вид:
,
при этом уравнение прямой получает вид:
 (6)
(6)
А формула (5) получает вид
 (7)
(7)
Формула (7) применена только
для
 ,
следовательно, значения
,
следовательно, значения
 по ней получить нельзя, поэтому
по ней получить нельзя, поэтому
 находят по методу Эйлера, при этом для
получения более точного результата
поступают так: с начала по формуле (5)
находят значение
находят по методу Эйлера, при этом для
получения более точного результата
поступают так: с начала по формуле (5)
находят значение
 (8)
(8)
В точке
 а затем находится
а затем находится
 по
формуле (7) с шагом
по
формуле (7) с шагом

 (9)
(9)
После того как
 найдено дальнейшие вычисления при
найдено дальнейшие вычисления при
 производится по формуле (7)
производится по формуле (7)
 ….
….
Пример
В качестве примера проведем
расчеты по формулам усовершенствованного
метода
Эйлера с шагом h=0,1 для задачи Коши
 .
.
 ;
;






***

3. Модифицированный метод Эйлера
Повысить точность и устойчивость вычисления решения можно с помощью неявного метода Эйлера следующего вида.
Прогноз:
 (10)
(10)
Коррекция:
 (11)
(11)
Геометрически это означает,
что с начало определяется направление
интегральной кривой в исходной точке
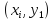 и во вспомогательной точке
и во вспомогательной точке
 ,
а в качестве окончательного направления
берется среднее значение этих направлений.
,
а в качестве окончательного направления
берется среднее значение этих направлений.
Благодаря более точной формуле интегрирования, погрешность метода пропорциональна уже квадрату шага интегрирования.
Пример
В качестве примера проведем
расчеты по формулам модифицированным
методом Эйлера с шагом
h=0,1 для задачи Коши
 .
.




Таблица Решение уравнения модифицированным методами Эйлера
|
xi |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
|
yi |
1 |
0.99 |
0.961 |
0.914 |
0.852 |
0.779 |
0.698 |
0.613 |
0.528 |
0.446 |
0.369 |
Точное решение имеет вид


4. Метод Рунге-Кутты
Воспользовавшись хорошо зарекомендовавшей себя формулой Симпсона, можно получить еще более точную формулу для решения задачи Коши для ОДУ первого порядка - широко используемого в вычислительной практике метода Рунге-Кутты.
В формуле Симпсона для приближенного вычисления определенного интеграла используются значения подинтегрального выражения в трех точках. В интеграле их всего две, поэтому введем дополнительную точку в середине отрезка [xi+1 , xi].

тогда можно определить так


Полученное выражение является
неявным, так как в правой части содержатся
еще не определенные значения
функции yi+h/2 и yi+1.
Чтобы воспользоваться этой формулой,
надо использовать некоторое приближение
для вычисления этих значений
 .
.

При использовании различных методов приближенного вычисления этих величин, получаются выражения для методов Рунге-Кутты различного порядка точности.
Алгоритм Рунге-Кутты четвертого порядка - (погрешность порядка h4):

где




Алгоритм четвертого порядка требует на каждом шаге четырех вычислений функции соответственно, но является весьма точным.
