Лаб 1
.docxМатематическое описание и моделирование случайных величин и случайных векторов
Случайной величиной называется
скалярная величина
 ,
значение которой заранее не известно.
В тоже время можно указать некую числовую
меру (вероятность) того, что это значение
будет принадлежать той или иной заранее
определенной области значений. Любое
значение случайной величины
,
значение которой заранее не известно.
В тоже время можно указать некую числовую
меру (вероятность) того, что это значение
будет принадлежать той или иной заранее
определенной области значений. Любое
значение случайной величины
 будем обозначать как
будем обозначать как
 .
.
Введем понятие выборочного пространства,
под которым понимается множество точек
 -мерного
пространства, в простейшем случае ‑
множество
-мерного
пространства, в простейшем случае ‑
множество
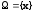 всех действительных чисел на числовой
оси. Будем называть их элементарными
событиями. На множестве можно ввести
класс подмножеств
всех действительных чисел на числовой
оси. Будем называть их элементарными
событиями. На множестве можно ввести
класс подмножеств
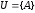 ,
включающий все открытые
,
включающий все открытые
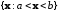 ,
закрытые
,
закрытые
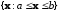 и полуоткрытые интервалы
и полуоткрытые интервалы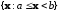 ,
,
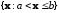 ,
где
,
где
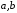 – заданные действительные числа,
принимающие произвольные известные
значения, в том числе и
– заданные действительные числа,
принимающие произвольные известные
значения, в том числе и
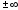 .
Данный класс подмножеств будем называть
возможными событиями.
.
Данный класс подмножеств будем называть
возможными событиями.
Для любого события
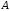 вводится действительная скалярная
функция (вероятностная мера)
вводится действительная скалярная
функция (вероятностная мера)
 ,
такая что
,
такая что
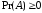 ,
,
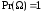 и для любой последовательности событий
и для любой последовательности событий
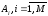 таких,
что
таких,
что
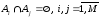 выполняется
выполняется
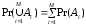 .
.
Такую функцию будем назвать вероятностью
события
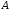 .
.
Случайная величина считается заданной,
если определена функция, позволяющая
вычислить вероятность того, что эта
случайная величина примет заданное
значение, будет принадлежать заданному
интервалу или их набору. В качестве
такой функции, определяющей свойства
случайной величины, рассматривается
функция распределения вероятностей
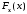 (интегральная функция распределения
вероятностей), являющаяся действительной
скалярной функцией скалярного аргумента
(интегральная функция распределения
вероятностей), являющаяся действительной
скалярной функцией скалярного аргумента
 и определяющая вероятность того, что
случайная величина
и определяющая вероятность того, что
случайная величина
 принадлежит полуоткрытому интервалу
принадлежит полуоткрытому интервалу
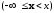 .Таким
образом,
.Таким
образом,
 .
.
Функция
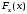 является неотрицательной неубывающей
функцией, удовлетворяющей условиям
является неотрицательной неубывающей
функцией, удовлетворяющей условиям
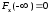 ,
,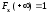 .
.
Другой характеристикой случайной величины, однозначно определяющей ее свойства, является плотность распределения вероятностей (дифференциальная функция распределения), которая задается как
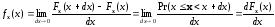 .
.
Индекс снизу у функций
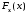 ,
,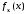 указывает на случайную величину, которой
он соответствует и далее может опускаться.
Далее также будем иногда использовать
обозначение
указывает на случайную величину, которой
он соответствует и далее может опускаться.
Далее также будем иногда использовать
обозначение
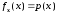 и термин плотность распределения или
просто – плотность. С учетом представленных
ранее соотношений можно записать, что
и термин плотность распределения или
просто – плотность. С учетом представленных
ранее соотношений можно записать, что
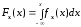 ,
,
 .
.
Последнее условие называется условием
нормировки плотности распределения.
Следует также отметить, что для функции
распределения при малых
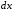 выполняется
выполняется
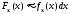 .
.
Обобщением понятия случайной величины для многомерных данных является понятие случайного вектора.
Случайным вектором называется
вектор, каждая компонента которого
является случайной величиной
 .
Значение этого вектора будем обозначать
как
.
Значение этого вектора будем обозначать
как
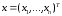 .
Свойства случайного вектора задаются
совместной многомерной функцией
распределения вероятностей и совместной
плотностью распределения вероятностей
.
Свойства случайного вектора задаются
совместной многомерной функцией
распределения вероятностей и совместной
плотностью распределения вероятностей
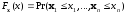 ,
,
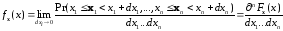 ,
,
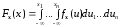 ,
,
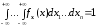
Пусть
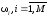 обозначают совокупность некоторых
событий, имеющих вероятности появления
обозначают совокупность некоторых
событий, имеющих вероятности появления
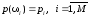 ,
такие что
,
такие что
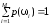 .
Вероятности
.
Вероятности
 в этом случае трактуются как априорные
вероятности событий или классов. Вводятся
также условные плотности распределения
вектора
в этом случае трактуются как априорные
вероятности событий или классов. Вводятся
также условные плотности распределения
вектора
 :
:
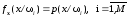 ,
которые трактуются как апостериорные
плотности распределения, каждая из
которых описывает распределение
,
которые трактуются как апостериорные
плотности распределения, каждая из
которых описывает распределение
 при условии возникновения фиксированной
ситуации появления соответствующего
события. При этом плотность распределения
при условии возникновения фиксированной
ситуации появления соответствующего
события. При этом плотность распределения
 может быть представлена как
может быть представлена как
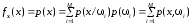 .
.
Здесь
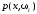 называется совместной плотностью
величины
называется совместной плотностью
величины
 и события
и события
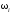 ,
для которой действует формула Байеса:
,
для которой действует формула Байеса:
 .
(1)
.
(1)
Вероятность
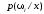 называется апостериорной вероятностью
события.
называется апостериорной вероятностью
события.
Аналогичным (1) образом вводятся условные
плотности распределения двух случайных
векторов (случайных величин)
 и
и
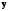
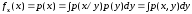 ,
,
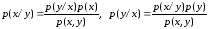 ,
,
где
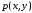 ,
,
 (
(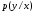 )
определяют соответственно совместную
плотность случайных векторов
)
определяют соответственно совместную
плотность случайных векторов
 и
и
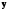 и плотность распределения вектора
и плотность распределения вектора
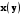 при фиксированном значении другого
вектора
при фиксированном значении другого
вектора
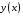 .
.
Здесь и далее интегралы понимаются как
многократные, а если область интегрирования
не указана конкретно, то пределы по
каждой компоненте случайного вектора
предполагаются заданными от
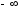 до
до
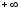 .
.
Если
 и
и
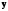 статистически независимы, то
статистически независимы, то
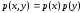 ,
,
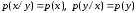 .
.
Для случайных векторов (величин) вводятся статистические характеристики, являющиеся параметрами безусловных и условных плотностей распределения вероятностей. Из них основными являются моменты случайного вектора и, прежде всего, вектор математического ожидания и матрица ковариации (дисперсия для одномерной случайной величины). Они определяются и обозначаются следующим образом:
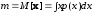 ,
,
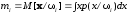 ,
,
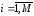 ,
,
 ,
,
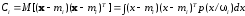 ,
,
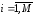 .
.
Элементы любой матрицы ковариации можно представить в виде
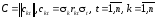 ,
,
где
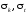 – средние квадратичные отклонения
(СКО), определяемые как корни квадратные
от дисперсий
– средние квадратичные отклонения
(СКО), определяемые как корни квадратные
от дисперсий
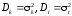 соответствующих компонентов случайного
вектора;
соответствующих компонентов случайного
вектора;
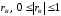 – являются коэффициентами корреляции
компонентов случайного вектора. Значения
– являются коэффициентами корреляции
компонентов случайного вектора. Значения
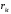 при
при
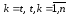 равны
единице, то есть диагональные элементы
матрицы ковариации соответствуют
дисперсиям компонентов случайного
вектора
равны
единице, то есть диагональные элементы
матрицы ковариации соответствуют
дисперсиям компонентов случайного
вектора
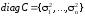 .
.
Соответственно в случае
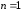 при описании случайной величины вместо
матрицы фактически используется
скалярная величина, называемая дисперсией
при описании случайной величины вместо
матрицы фактически используется
скалярная величина, называемая дисперсией
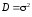 .
Величина
.
Величина
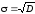 называется
среднеквадратичным отклонением (СКО).
Всё сказанное аналогичным образом
распространяются и на условные матрицы
ковариации
называется
среднеквадратичным отклонением (СКО).
Всё сказанное аналогичным образом
распространяются и на условные матрицы
ковариации
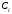 ,
,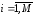 .
.
Важным частным случаем случайного
вектора является гауссовский случайный
вектор (случайная величина) (ГСВ). Его
распределение определяется только
двумя параметрами математическим
ожиданием
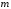 и матрицей ковариации
и матрицей ковариации
 .
Плотность распределения ГСВ обозначается
и выражается следующим образом:
.
Плотность распределения ГСВ обозначается
и выражается следующим образом:
 ,
(2)
,
(2)
где
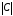 – определитель матрицы. Величина
– определитель матрицы. Величина
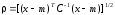 называется расстоянием Махалонобиса.
Если матрица ковариации является
единичной
называется расстоянием Махалонобиса.
Если матрица ковариации является
единичной
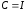 (случай, когда все компоненты случайного
вектора независимы и имеют дисперсии,
равные единице), то расстояние Махаланобиса
переходит в расстояние Евклида
(случай, когда все компоненты случайного
вектора независимы и имеют дисперсии,
равные единице), то расстояние Махаланобиса
переходит в расстояние Евклида
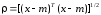 .
.
Следует также отметить, что любое
линейное преобразование ГСВ с параметрами
 ,
задаваемое прямоугольной матрицей
,
задаваемое прямоугольной матрицей
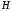 преобразует его к новому ГСВ
преобразует его к новому ГСВ
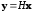 с параметрами
с параметрами
 .
.
В задачах статистического анализа
данных часто используются выборочные
параметры распределения СВ, которые
определяются в общем случае на основе
обучающей выборки значений случайного
вектора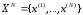 .
К таким параметрам, в частности, относятся
выборочное математическое ожидание
.
К таким параметрам, в частности, относятся
выборочное математическое ожидание
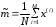
и
выборочная матрица ковариации, а частном
случае (при
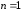 )
– дисперсия СВ
)
– дисперсия СВ
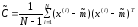 ,
,
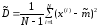 .
.
Необходимо отметить, что для вычисления всех указанных характеристик среда MATLAB предоставляет стандартные функции, которые читатель может найти самостоятельно.
В представленном ниже скрипте проводится визуализации графика одномерной плотности распределения гауссовской случайной величины с различными математическими ожиданиями и дисперсией, а также графики двумерного случайного вектора с различными коэффициентами корреляции компонентов. Для вычисления значений одномерной и многомерной плотностей распределения вероятностей использовались стандартные функции среды MATLAB normpdf(x,m,s) и mvnpdf(x,m,C). Кроме того, приводится отображение линий постоянного уровня двумерной плотности распределения, наглядно отражающих области локализации значений случайного вектора. Визуализация графиков для функций распределения может быть выполнена совершенно аналогично на основе использования стандартных функция среды normсdf(x,m,s) и mvnсdf(x,m,C).
% Пример 1
% Визуализация графиков гауссовской плотности распределения вероятностей
clear all;
close all;
% 1. Визуализация плотности распределения для скалярной случайной величины
m=1.0; s=3.0; % математическое ожидание и среднеквадратичное отклонение
x=[-4:0.1:4]; % массив значений случайной величины
f=normpdf(x,m,s); % массив значений плотности распределения
figure(1);
grid on; hold on;
axis([-4 4 0 max(f)+0.1]); % установка границ поля графика по осям
plot(x,f,'-b');
title('Гауссовская плотность распределения случайной величины');
xlabel('x'); ylabel('f');
strv1='m='; strv2=num2str(m); strv3=' s='; strv4=num2str(s);
text(-0.5, 0.5*max(f),[strv1, strv2, strv3, strv4], 'FontSize',12);
legend('f=normpdf(x,m,s)'); hold off;
% 2. Визуализация плотности распределения двумерного случайного вектора
m=[0.0 0.0]; % вектор математического ожидания
D1=1.0; D2=1.0; % дисперсии компонентов
r12=-0.7; % и коэффициент корреляции
r21=r12;
C = [D1, sqrt(D1*D2)*r12; % матрица ковариации
sqrt(D2*D1)*r21, D2];
x1=[-4:0.1:4];
x2=[-4:0.1:4];
[X1,X2]=meshgrid(x1,x2); % матрицы значений координат случайного вектора
f2=mvnpdf([X1(:) X2(:)],m,C); % массив значений плотности распределения
f3=reshape(f2,length(x1),length(x2)); % матрица значений плотности распределения
figure(2);
grid on; hold on;
caxis([min(f3(:))-0.5*range(f3(:)),max(f3(:))+0.5*range(f3(:))]); % установка цветовой гаммы
axis([-4 4 -4 4 0 max(f3(:))+0.1]); % установка границ роля графика по осям
surf(x1,x2,f3);
title('Гауссовская плотность распределения ');
xlabel('x1'); ylabel('x2'); zlabel('f=mvnpdf(x,m,C)');
strv1='r12= '; strv2=num2str(r12);
text(2, 0.5, 0.5*max(f3(:)),[strv1, strv2], 'BackgroundColor',[.8 .8 .8],'FontSize',12);
hold off;
Моделирование простейших случайных
величин на основе стандартных датчиков
случайных чисел. Базовым алгоритмом,
на основе которого могут быть получены
алгоритмы и программы моделирования
любых случайных величин, является
алгоритм (датчик) стандартной равномерно
распределенной случайной величины
 .
Закон распределения, математическое
ожидание и дисперсия этой величины
определяется соотношениями
.
Закон распределения, математическое
ожидание и дисперсия этой величины
определяется соотношениями
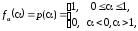
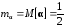 ,
,
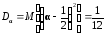
Основные принципы построения алгоритмов и программной реализации датчиков равномерной случайной величины (РСВ) подробно рассмотрены в [1], и в настоящее время реализованы в стандартных датчиках программных средств и систем в виде готовых встроенных функций rand (в MATLAB). Примеры обращения к этому датчику представлены в следующем скрипте:
% Пример 2
% Примеры обращения к датчику стандартной РСВ и построение гистограммы
clear all;
n=7;
m=3;
alfa=rand % генерация значения случайной величины СВ
row_alfa=rand(1,n) % генерация вектора-строки из n значений СВ
col_alfa=rand(m,1) % генерация вектора-столбца из m значений СВ
mat_alfa=rand(m,n) % генерация и визуализация матрицы из m*n значений СВ
% Построение гистограммы РСВ для выборки из тысячи реализаций
figure; hold on;
title('Гистограмма равномерной случайной величины');
N=10000; % объем выборки
XN=rand(N,1);
x=0.025:0.05:0.975; % задание центров и границ интервалов гистограммы
[g, y]=hist(XN,x); % построение ненормированной гистограммы
bar(y, g); % (без деления частот на N)
hold off;
Равномерное распределение в интервале
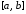 реализует величина
реализует величина
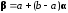 ,
где
,
где
 ‑ РСВ, распределенная в интервале
[0,1]. Математическое ожидание и дисперсия
‑ РСВ, распределенная в интервале
[0,1]. Математическое ожидание и дисперсия
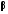 определяются как
определяются как
 ,
,
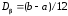 .
.
Алгоритм генерации значений гауссовской
случайной величины (ГСВ)
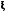 ,
имеющей параметры
,
имеющей параметры
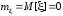 и
и
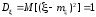 ,
основывается на результатах центральной
предельной теоремы, согласно которой
сумма
,
основывается на результатах центральной
предельной теоремы, согласно которой
сумма
 значений одинаково распределенных и
независимых случайных величин имеет в
пределе (при
значений одинаково распределенных и
независимых случайных величин имеет в
пределе (при
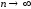 )
гауссовское распределение. Это означает,
что, имея датчик РСВ, очередное значение
ГСВ
)
гауссовское распределение. Это означает,
что, имея датчик РСВ, очередное значение
ГСВ
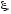 может быть получено как сумма следующего
вида:
может быть получено как сумма следующего
вида:
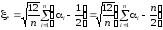 ,
,
где
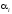 – независимые значения равномерной
случайной величины
– независимые значения равномерной
случайной величины
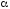 ,
получаемые при последовательных
обращениях к датчику. Особенно удобно
выбирать
,
получаемые при последовательных
обращениях к датчику. Особенно удобно
выбирать
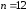 ,
тогда получается простейший алгоритм
генерации ГСВ
,
тогда получается простейший алгоритм
генерации ГСВ
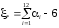 .
.
Необходимо отметить, что в среде MATLAB имеется готовый датчик значений стандартной гауссовской случайной величины в вид встроенной функции randn.
В табл. 1 приводятся типовые алгоритмы моделирования случайных величин с часто встречающимися законами распределения.
Таблица 1. Алгоритмы моделирования случайных величин
|
№ |
Наименование |
Обозначение, параметры сдвига, масштаба, формы |
Плотность распределения, математическое ожидание m и дисперсия D |
Алгоритм генерации |
|
1 |
Равномерное распределение |
R : a, b |
|
|
|
2 |
Биномиальное распределение |
B:n,p |
|
|
|
3 |
Распределение Пуассона |
P: |
|
|
|
4 |
Гауссовское (нормальное) распределение |
N : μ, |
|
|
|
5 |
Показательное распределение |
E : b |
|
|
|
6 |
Распределение Рэлея |
Rl:σ |
|
|
|
7 |
Логнормальное распределение |
L : , |
|
|
|
8 |
Гамма-распределение |
: b, c
|
|
|
|
9 |
Распределение Эрланга |
Er : b, c, |
|
|
|
10 |
Бета-распределение |
: v, w |
|
|
Моделирование случайных векторов с
заданной матрицей ковариации. Для
гауссовских случайных векторов можно
относительно просто сгенерировать
реализации, обладающие заданной матрицей
ковариации. Здесь стандартным способом
получения реализаций случайного вектора
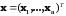 с
нулевым математическим ожиданием и
матрицей ковариации вида
с
нулевым математическим ожиданием и
матрицей ковариации вида
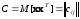 является использование разложения
Холецкого. Как известно, вектор
является использование разложения
Холецкого. Как известно, вектор
 может быть получен на основе линейного
преобразования вектора
может быть получен на основе линейного
преобразования вектора
 ,
компоненты которого являются независимыми
гауссовскими стандартными случайными
величинами
,
компоненты которого являются независимыми
гауссовскими стандартными случайными
величинами
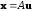 ,
,
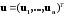 ,
,
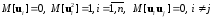 . (3)
. (3)
Здесь матрица
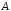 ,
выполняющая линейное преобразование,
удовлетворяет уравнению
,
выполняющая линейное преобразование,
удовлетворяет уравнению
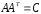 .
Матрица
.
Матрица
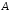 является нижней треугольной матрицей
(
является нижней треугольной матрицей
(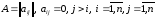 ).
Подобное представление называется
факторизацией ковариационной матрицы
(факторизацией Холецкого).
).
Подобное представление называется
факторизацией ковариационной матрицы
(факторизацией Холецкого).
Следует отметить, что при выполнении
преобразования (3) для случая негауссовского
вектора
 с теми же параметрами вектор
с теми же параметрами вектор
 будет иметь негауссовское распределение
с таким же (нулевым) математическим
ожиданием и матрицей ковариации
будет иметь негауссовское распределение
с таким же (нулевым) математическим
ожиданием и матрицей ковариации
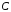 .
.
Разложение Холецкого в
среде MATLAB
возможно как для действительных
положительно определенных, так и для
комплексных эрмитовых матриц. Оператор
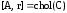 для квадратной симметричной
матрицы
для квадратной симметричной
матрицы
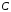 возвращает верхнюю треугольную матрицу
возвращает верхнюю треугольную матрицу
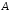 ,
а также скалярную величину
,
а также скалярную величину
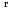 ,
диагностирующую результаты факторизации.
Если
,
диагностирующую результаты факторизации.
Если
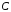 положительно определенная, хорошо
обусловленная матрица, то
положительно определенная, хорошо
обусловленная матрица, то
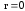 ,
a матрица
,
a матрица
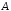 такова, что
такова, что
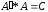 и совпадает по размерности
с
и совпадает по размерности
с
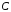 .
В противном случае выдается положительное
целое число
.
В противном случае выдается положительное
целое число
 ,
а
,
а
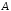 – верхняя треугольная
матрица порядка
– верхняя треугольная
матрица порядка
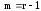 ,
такая что
,
такая что
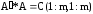 .
По сути это означает, что функция
.
По сути это означает, что функция
 самостоятельно выбирает размерность
той части входной матрицы, для которой
еще выполняются условия положительной
определенности. Следующая функция
обеспечивающую генерацию реализации
случайного вектора
самостоятельно выбирает размерность
той части входной матрицы, для которой
еще выполняются условия положительной
определенности. Следующая функция
обеспечивающую генерацию реализации
случайного вектора
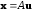 .
.
% Функция для генерации совокупности гауссовских случайных векторов с нулевым математическим ожиданием и матрицей ковариации С
function [x,m]=randncor(n,N,C)
% n-исходный порядок матрицы ковариации C (размер n*n)
% N-количество генерируемых векторов
% формирование верхней треугольной матрицы разложения Холецкого
% с определением порядка матрицы и размерности генерируемых векторов
[A,r]=chol(C);
% определение размерности генерируемых векторов
if r==0, m=n; else m=r-1; end;
% генерация матрицы реализаций m*N гауссовских независимых случайных величин
u=randn(m,N);
% получение матрицы N реализаций гауссовских случайных векторов размерности m
x=A'*u;
Модуль randncor является отдельным m-файлом и хранится в директории с исполняемым m-сценарием.
Следующий пример позволяет оценить работу алгоритма.
% Пример 3
% Генерация реализаций случайного вектора с заданной матрицей ковариации
clear all;
close all;
n=3; % n-исходный порядок матрицы ковариации
N=1000; % количество генерируемых векторов
C = [ 1, 0.9, -0.5;
0.9, 1, -0.5;
-0.5, -0.5, 1 ]; %матрица ковариации
[x,m]=randncor(n,N,C); %обращение к функции генерации реализаций случайных веторов
% Оценка выборочной матрицы ковариации
C_=zeros(m,m);
for i=1:N
C_=C_+x(:,i)*x(:,i)';
end;
C_=C_/(N-1) % выборочная матрица ковариации
% Визуализация сгенерированных реализаций случайного вектора
P=x;
% 3D-отображение кластера
T=ones(1,N); % формирование маркеров реализаций случайных векторов
figure(1);
plotpv(P,T);
% 2D-отображение кластеров компонентов реализаций случайного вектора
T=0.5*ones(1,N); % формирование маркеров для первой и второй компоненты
figure(2);
plotpv(P(1:2,:),T);
T=1.5*ones(1,N); %формирование маркеров для второй и третьей компоненты
figure(3);
plotpv(P(2:3,:),T);
Во
многих случаях на практике матрица
ковариации является плохо обусловленной,
при этом не всегда бывает удобно
использовать «плавающую» размерность
генерируемых с использованием функции
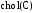 векторов. В подобных
случаях можно провести простейшую
регуляризацию матрицы ковариации,
модифицировав ее следующим образом
[2]:
векторов. В подобных
случаях можно провести простейшую
регуляризацию матрицы ковариации,
модифицировав ее следующим образом
[2]:
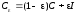 ,
,
где
 –
малое относительно диагональных
элементов
–
малое относительно диагональных
элементов
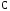 положительное число;
положительное число;
 –
единичная матрица соответствующей
размерности.
–
единичная матрица соответствующей
размерности.
Помимо рассмотренных, при решении задачах синтеза и анализа алгоритмов обработки информации возникают вопросы моделирования случайных процессов (случайных сигналов) и случайных полей (изображений). Алгоритмы генерации реализаций случайных процессов и полей являются существенно более сложными и рассматриваются в специальной литературе. Достаточно детальный анализ этих алгоритмов с примерами реализации в среде MATLAB приведен в работе [1].

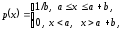
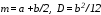
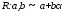 ,
,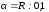 –
значение,
получаемое при обращении к датчику
РСВ в диапазоне [0,1]
–
значение,
получаемое при обращении к датчику
РСВ в диапазоне [0,1] ,
,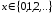 ,
,

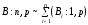
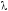
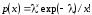 ,
,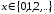
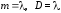
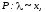
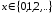 ,
,
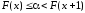 ,
,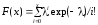
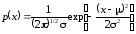 ,
,
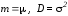
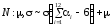
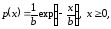
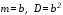
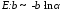
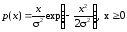 ,
,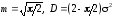
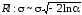
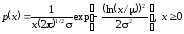 ,
,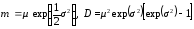
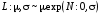
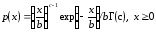
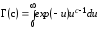 – гамма-функция,
– гамма-функция,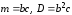
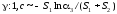 ,
,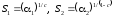 ,
,
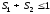 ,
,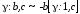 ,
при
,
при
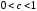 ,
,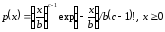 ,
,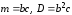
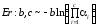 ,
c – целое
число
,
c – целое
число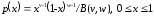 ,
,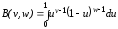 – бета-функция,
– бета-функция,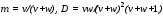
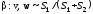 ,
,
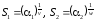 ,
,