
- •Глава 1. Матрицы и определители
- •§1. Матрицы
- •1. Понятие матрицы
- •2. Квадратные матрицы
- •3. Действия с матрицами
- •Тогда суммарная производительность (за рабочий день) будет:
- •§2. Определители. Свойства. Вычисление
- •§3. Обратная матрица.
- •§4. Ранг матрицы
- •Идея практического метода вычисления ранга матрицы
- •Типовой пример. Найти ранг и указать какой-нибудь базисный минор матрицы .
- •Глава 2
- •§2. Решение линейных систем с помощью обратной матрицы. Правило Крамера. Теорема Кронекера-Капелли
- •§2. Метод Гаусса (метод последовательного исключения неизвестных) решения систем линейных уравнений
- •§4. Однородная система линейных алгебраических уравнений
- •Глава 3 линейные (векторные) пространства
- •§1. Понятие линейного пространства.
- •§ 2. Линейная зависимость и независимость систем векторов. Базис и размерность
- •Типовые примеры.
- •§ 3. Евклидовы пространства
- •Типовые примеры.
- •3.Матрица Грамма.Матрицей Грамадля системы векторовназывается симметричная матрица вида
- •4. Ортогональное разложение векторов. Говорят, что векторортогонален к подпространству, если векторортогонален любому вектору из этого подпространства.
- •§4.Унитарное пространство
- •§5. Определение линейного оператора. Матрица линейного оператора.
- •§ 5. Собственные векторы и собственные значения матриц.
- •§6. Симметрические операторы. Квадратичные формы и их применения
- •Типовые примеры.
Тогда суммарная производительность (за рабочий день) будет:

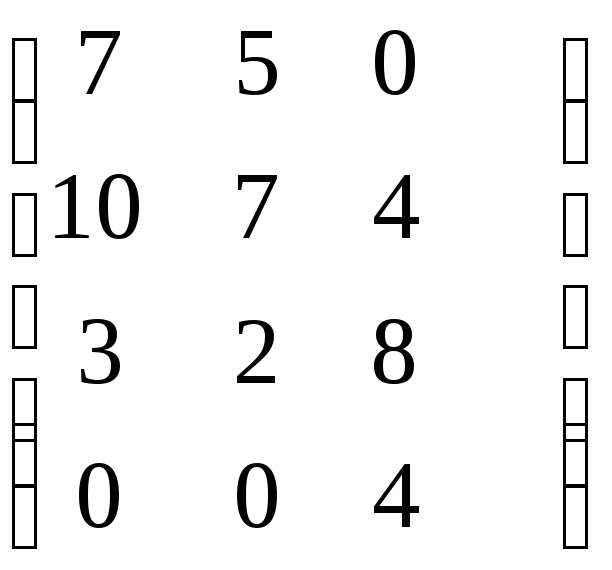 =
=

Расход сырья на каждом предприятии найдется из выражения:
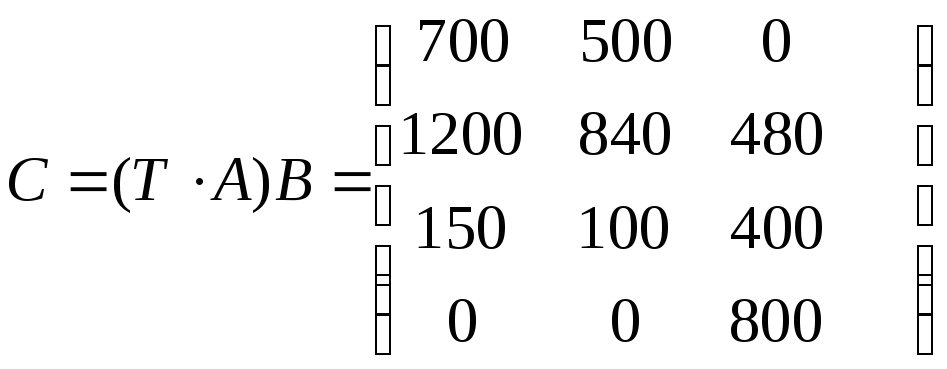
 =
=

Суммарное
количество I
и II
видов сырья по всем предприятиям можно
получить, умножив матрицу – строку
![]() на матрицу
на матрицу![]()
 =
=![]() .
.
3. Размеры кредитов определяются стоимостью сырья, используемого каж-
дым
предприятием, путем умножения матрицы
![]() на матрицу
на матрицу![]() .
.
![]() =
=![]()
![]() =1
917 900. Размер кредитов всем предприятиям
равен 1 917 900 руб.◄
=1
917 900. Размер кредитов всем предприятиям
равен 1 917 900 руб.◄
§2. Определители. Свойства. Вычисление
1.
Квадратной матрице
![]()
![]() -го порядка
соответствует число, называемое
определителем
(или детерминантом).
Обозначается определитель:
-го порядка
соответствует число, называемое
определителем
(или детерминантом).
Обозначается определитель:
![]() ,
,![]() ,
,![]() .
.
|
Если |
|
- определитель 1-го порядка. | |
|
Если |
|
- определитель 2-го порядка. | |
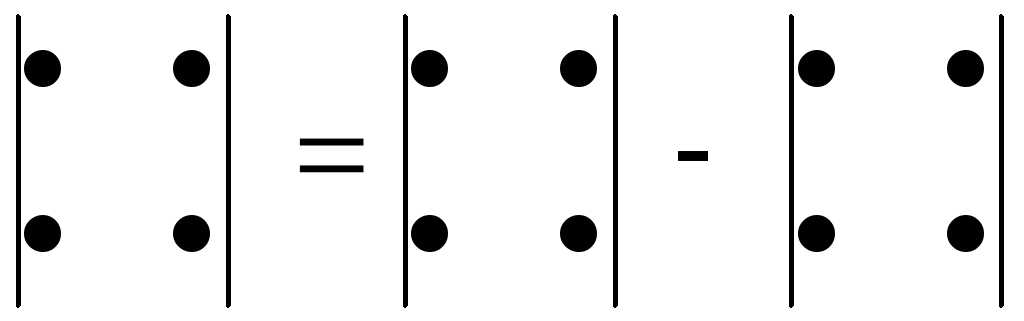


Схема
вычисления:
![]()
![]() .
.
|
Если
|
|
- определитель 3-го порядка. |
Определитель третьего порядка можно вычислять по правилу треугольников (правилу Саррюса).
Схема вычисления:

![]()

Типовые примеры. Вычислить определитель.
1)
![]() .
.
►![]() .◄
.◄
2)
![]()
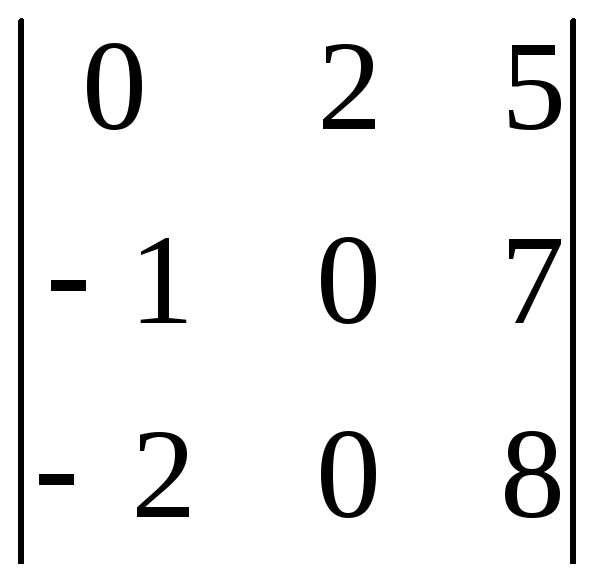 .
►
.
►![]()
=-28 +16= - 12.◄
3)
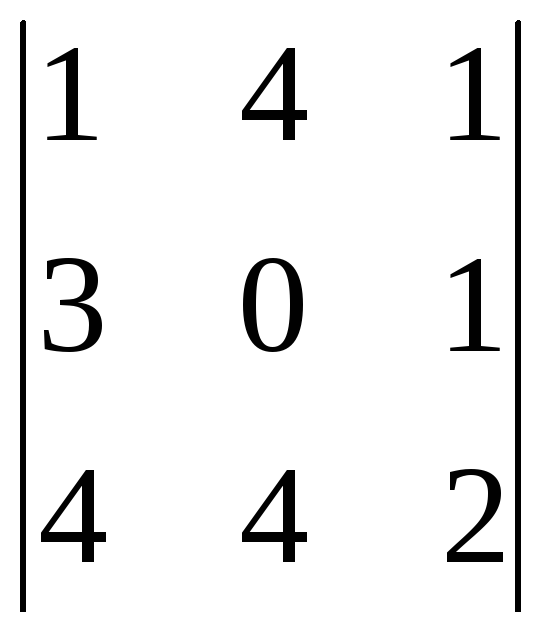 .
►
.
►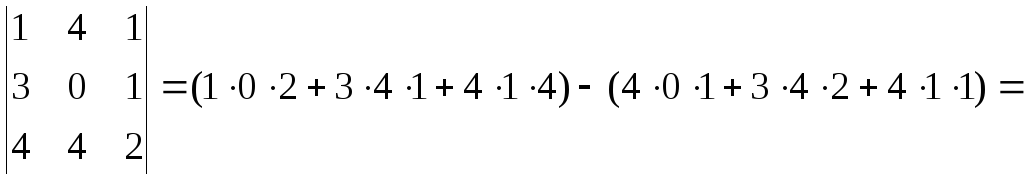
=(0+12+16)-(0+12+4)=28-16=12. ◄
Прежде,
чем сформулировать определение
определителя
![]() -го
порядка, рассмотрим одно вспомогательное
понятие.
-го
порядка, рассмотрим одно вспомогательное
понятие.
2.
Перестановки.
Перестановкой
чисел
![]() называют расположение этих чисел в
каком-либо определенном порядке (не
обязательно в порядке возрастания).
НаТиповой пример,
называют расположение этих чисел в
каком-либо определенном порядке (не
обязательно в порядке возрастания).
НаТиповой пример,![]() – одна из возможных перестановок чисел
– одна из возможных перестановок чисел![]() .
.
Число
различных перестановок, которые можно
составить из чисел
![]() ,
равно произведению
,
равно произведению![]() (читается: «n
факториал»).
(читается: «n
факториал»).
Пусть
дана какая-то перестановка
![]() чисел
чисел![]() .
Назовеминверсией
(или беспорядком)
в перестановке
.
Назовеминверсией
(или беспорядком)
в перестановке
![]() любую пару чисел в этой перестановке,
из которых большее число расположено
левее меньшего.
любую пару чисел в этой перестановке,
из которых большее число расположено
левее меньшего.
Типовой
пример. В
перестановке
![]() имеются 3 инверсии: их образуют пары
имеются 3 инверсии: их образуют пары![]() ,
,![]() ,
,![]() .
.
Условимся
обозначать общее число инверсий в
перестановке
![]() символом
символом![]() .
Перестановка
.
Перестановка![]() называетсячетной,
если число
называетсячетной,
если число
![]() – четное, инечетной,
если число
– четное, инечетной,
если число
![]() – нечетное.
– нечетное.
Так
в рассмотренном выше Типовой примере
перестановка содержала 3 инверсии и,
следовательно, является нечетной.
Заметим, что перестановка
![]() не содержит ни одной инверсии, иначе
говоря, содержит 0 инверсий. Следовательно,
эта перестановка является четной.
не содержит ни одной инверсии, иначе
говоря, содержит 0 инверсий. Следовательно,
эта перестановка является четной.
3.
Определитель
![]() -го
порядка.
Определителем
-го
порядка.
Определителем
![]() -го
порядка (или определителем матрицы
-го
порядка (или определителем матрицы![]() -го
порядка) называется число, равное
-го
порядка) называется число, равное
 ,
(4)
,
(4)
где
суммирование распространяется на все
перестановки
![]() ,
которые можно составить из чисел
,
которые можно составить из чисел![]() .
Количество слагаемых в правой части
равенства (4) равно
.
Количество слагаемых в правой части
равенства (4) равно![]() ,
так как количество всех перестановок
множества из
,
так как количество всех перестановок
множества из![]() элементов равно
элементов равно![]() .
.
4.
Свойства определителей.
Сформулируем без доказательства ряд
свойств, которыми обладает произвольный
определитель
![]() -го
порядка.
-го
порядка.
1)
Свойство
равноправности строк и столбцов. При
транспонировании величина определителя
сохраняется, т.е.
![]() .Это свойство
означает полную равноправность строк
и столбцов и позволяет нам все последующие
свойства формулировать лишь для строк
и быть уверенными в справедливости их
и для столбцов.
.Это свойство
означает полную равноправность строк
и столбцов и позволяет нам все последующие
свойства формулировать лишь для строк
и быть уверенными в справедливости их
и для столбцов.
2) При перестановке местами 2-х строк определитель сохраняет свою абсолютную величину, но меняет знак на противоположный.
3)
Линейное свойство определителя. Если
все элементы
![]() -ой
строки определителя
-ой
строки определителя![]() -го
порядка представлены в виде суммы двух
слагаемых
-го
порядка представлены в виде суммы двух
слагаемых
![]()
![]() ,
,
то
исходный определитель можно представить
в виде суммы двух определителей, у
которых элементами
![]() -й
строки являются соответственно
-й
строки являются соответственно![]() и
и![]()
![]() ,
а все остальные строки – такие же, как
у исходного определителя.
При этом определители умножаются на
,
а все остальные строки – такие же, как
у исходного определителя.
При этом определители умножаются на
![]() и
и![]() соответственно:
соответственно:
 .
.
Конечно
линейное свойство справедливо и для
случая, когда
![]() -я
строка является линейной комбинацией
не двух, а нескольких строк. На этот
случай (любого конечного числа слагаемых)
сформулированное свойство обобщается
индукцией по числу слагаемых.
-я
строка является линейной комбинацией
не двух, а нескольких строк. На этот
случай (любого конечного числа слагаемых)
сформулированное свойство обобщается
индукцией по числу слагаемых.
Приведенные три свойства являются основными свойствами определителя. Все следующие свойства являются логическими следствиями трех основных свойств.
4)
Определитель
с двумя одинаковыми строками равен
нулю. В самом
деле, при перестановке двух одинаковых
строк, с одной стороны, определитель
![]() не изменится, а с другой стороны, в силу
свойства 2 изменит свой знак на
противоположный. Таким образом,
не изменится, а с другой стороны, в силу
свойства 2 изменит свой знак на
противоположный. Таким образом,![]() ,
т.е.
,
т.е.![]() или
или![]() .
.
5)
Умножение
всех элементов некоторой строки
определителя на число
![]() равносильно умножению определителя на
это число
равносильно умножению определителя на
это число![]() .
Иными словами, общий множитель всех
элементов некоторой строки определителя
можно вынести за знак этого определителя.
Это свойство вытекает из свойства 3 при
.
Иными словами, общий множитель всех
элементов некоторой строки определителя
можно вынести за знак этого определителя.
Это свойство вытекает из свойства 3 при
![]() .
.
6)
Если все
элементы некоторой строки определителя
равны нулю, то и сам определитель равен
нулю. Это
свойство вытекает из свойства 5 при
![]() .
.
7) Если элементы двух строк определителя пропорциональны, то определитель равен нулю. В самом деле, в силу свойства 5 множитель пропорциональности можно вынести за знак определителя, после чего останется определитель с двумя одинаковыми строками, который равен нулю согласно свойству 4.
8)
Если к элементам некоторой строки
определителя прибавить соответствующие
элементы другой строки, умноженные на
произвольный множитель
![]() ,
то величина определителя не изменится.
В самом деле, полученный в результате
указанного прибавления определитель
можно в силу свойства 3 разбить на сумму
двух определителей, первый из которых
совпадает с исходным, а второй равен
нулю в силу пропорциональности двух
строк и свойства 7.
,
то величина определителя не изменится.
В самом деле, полученный в результате
указанного прибавления определитель
можно в силу свойства 3 разбить на сумму
двух определителей, первый из которых
совпадает с исходным, а второй равен
нулю в силу пропорциональности двух
строк и свойства 7.
9)
Определитель произведения матриц. Если
![]() ,
где
,
где![]() и
и![]() – квадратные матрицы (одинакового
порядка), то
– квадратные матрицы (одинакового
порядка), то![]() .
.
5.
Вычисление определителей
![]() -го
порядка. Пусть дана матрица
-го
порядка. Пусть дана матрица![]()
![]() -го
порядка.Минором
любого элемента
-го
порядка.Минором
любого элемента
![]() называют определитель порядка
называют определитель порядка![]() ,
соответствующий той матрице, которая
получается из матрицы
,
соответствующий той матрице, которая
получается из матрицы![]() в результате вычеркивания
в результате вычеркивания![]() -й
строки и
-й
строки и![]() -го
столбца (т.е. той строки и того столбца,
на пересечении которых стоит элемент
-го
столбца (т.е. той строки и того столбца,
на пересечении которых стоит элемент![]() ).
Минор элемента
).
Минор элемента![]() будем обозначать символом
будем обозначать символом![]() .
.
Алгебраическим
дополнением
![]() элемента
элемента![]() матрицы
матрицы![]() называют минор
называют минор![]() этого элемента, умноженный на
этого элемента, умноженный на![]() ,
т.е.
,
т.е.
![]() .
.
ТЕОРЕМА.
Определитель
матрицы
![]()
![]() -го
порядка равен сумме произведений всех
элементов какой-нибудь одной фиксированной
строки на их алгебраические дополнения,
т.е. для любого
-го
порядка равен сумме произведений всех
элементов какой-нибудь одной фиксированной
строки на их алгебраические дополнения,
т.е. для любого![]() имеет место равенство
имеет место равенство
![]() ,
,
называемое
разложением определителя
![]() по элементам
по элементам![]() -й
строки.
-й
строки.
Аналогично
для
![]() имеет место разложение определителя
имеет место разложение определителя![]() по элементам
по элементам![]() -го
столбца:
-го
столбца:
![]() .
.
Методы вычисления определителей.
1) Разложение по строке или столбцу.
2) Метод обращения в нуль всех, кроме одного, элементов строки или столбца. Метод состоит в том, что с учетом свойств определителя при помощи какого-либо столбца (строки) путём умножения его на соответствующие числа и вычитания из остальных столбцов (строк), все элементы выбранной строки (столбца) кроме одного обращаются в нуль, принадлежащего вычитаемому столбцу (строке).
3) Метод приведения к треугольному виду. Алгоритм, предложенный в предыдущем пункте, используется для последовательного преобразования определителя к треугольному виду. Величина такого определителя равна произведению элементов главной диагонали.
Типовые примеры. Вычислить определитель.
1)
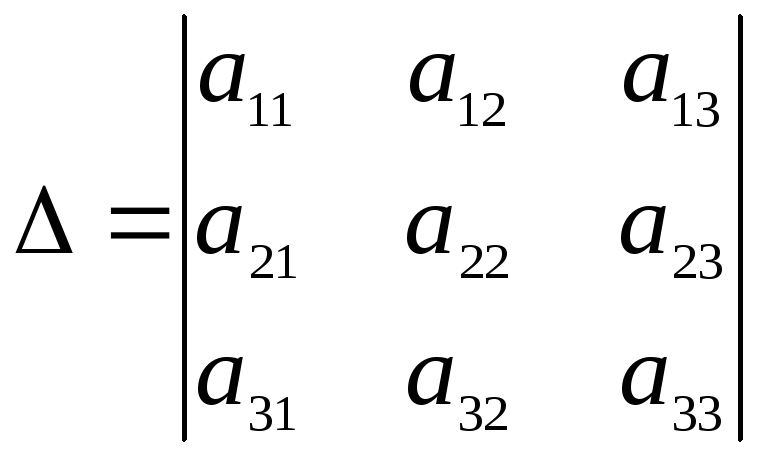 .
►Имеем
.
►Имеем![]() ,
или,
,
или,
например,
![]() ,
,
и т.д.◄
2)►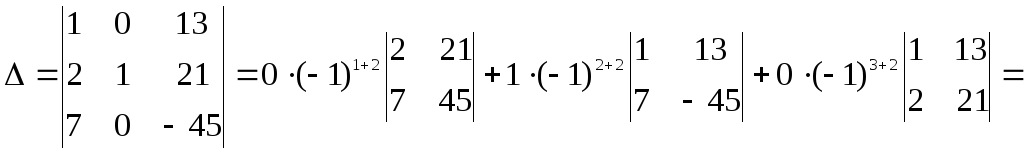 =0+(-45-91)+0= -136. ◄
=0+(-45-91)+0= -136. ◄
3)
 .
►Вычислим данный определитель 4-го
порядка с помощью разложения по 2-му
столбцу. Для этого найдем
.
►Вычислим данный определитель 4-го
порядка с помощью разложения по 2-му
столбцу. Для этого найдем![]() и
и![]() :
:
 Следовательно,
Следовательно,
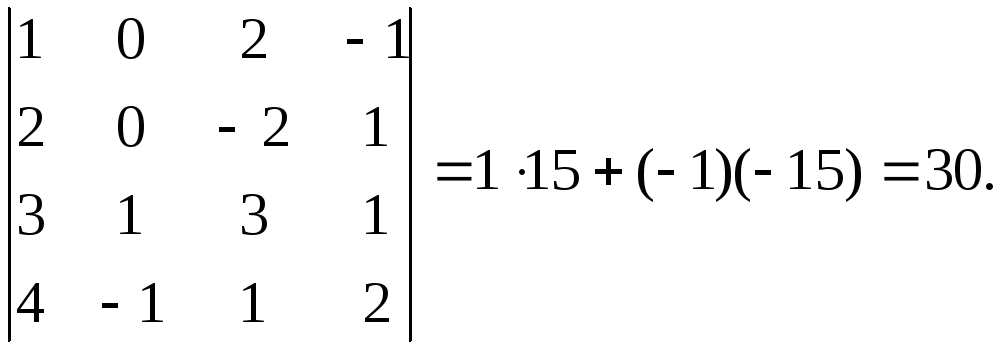 ◄
◄
4) Вычислить данный определитель четвёртого порядка с помощью разложения по строке или столбцу:
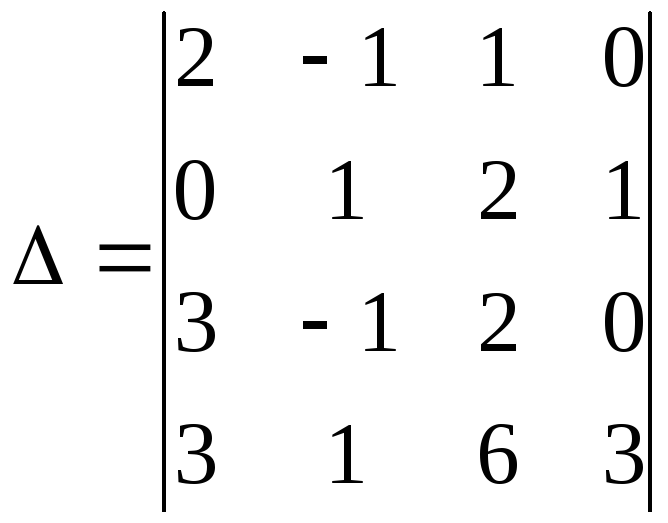
►Удобнее всего делать разложение по строке или столбцу, в которых встречается наибольшее число нулевых элементов. В данном случае – это четвёртый столбец. Итак, имеем
П олученные
в итоге два определителя третьего
порядка вычислим тем же методом. В
определителе
олученные
в итоге два определителя третьего
порядка вычислим тем же методом. В
определителе![]() нулевых элементов нет, поэтому можно
выбрать для разложения любой из столбцов,
наТиповой пример, первый. В
нулевых элементов нет, поэтому можно
выбрать для разложения любой из столбцов,
наТиповой пример, первый. В![]() единственный нулевой элемент находится
на пересечении первого столбца со второй
строкой. Для разнообразия будем разлагать
единственный нулевой элемент находится
на пересечении первого столбца со второй
строкой. Для разнообразия будем разлагать![]() по второй строке:
по второй строке:![]()
![]()
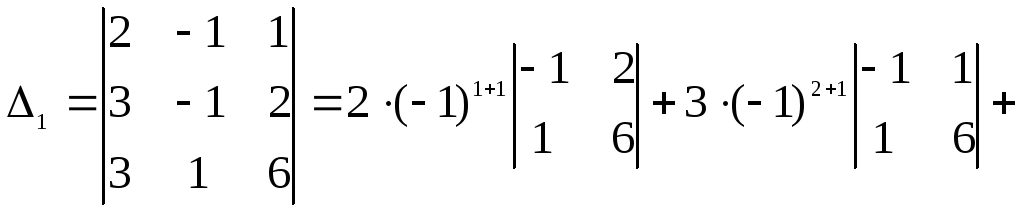
 .
.
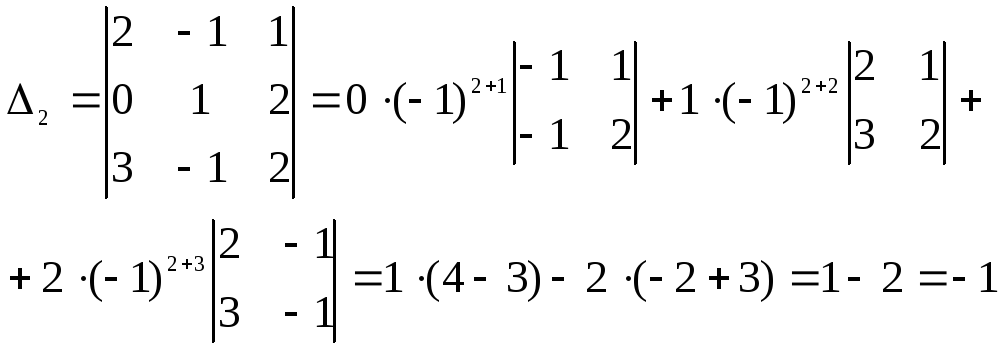 .
.
Таким образом окончательно получим
![]() .◄
.◄
5) Используя метод обращения в нуль всех, кроме одного, элементов строки или столбца вычислить определитель матрицы

►Будем обращать в нуль все, кроме первого, элементы первой строки. С этой целью вычтем из второго, третьего и четвёртого столбцов первый столбец, умноженный соответственно на 2, 3 и 4. Получим
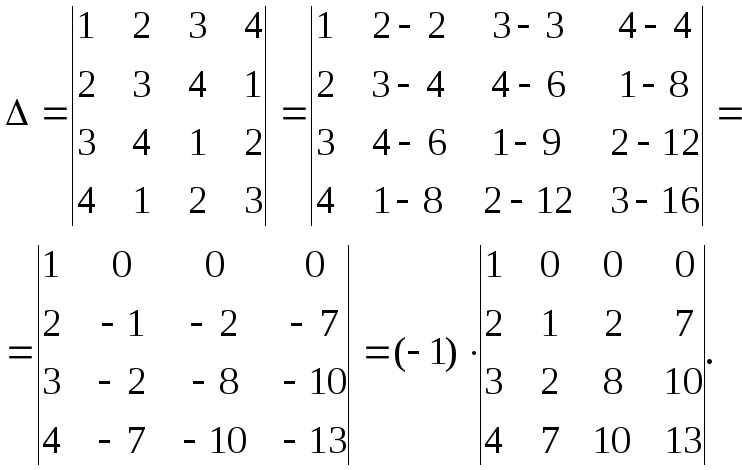
Представленный в таком виде определитель разложим по первой строке:
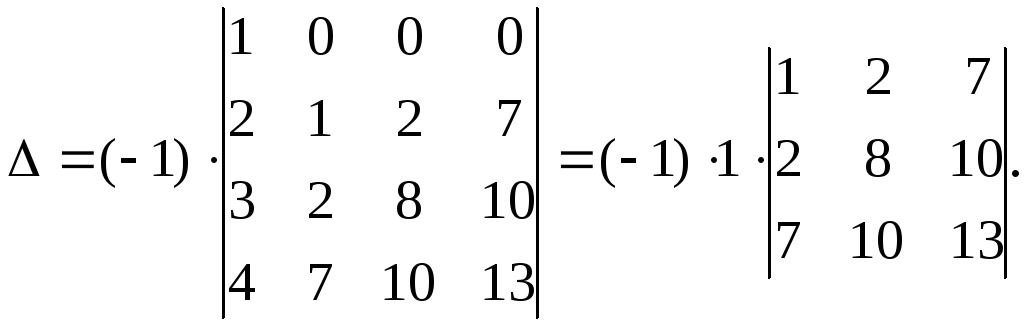
Определитель третьего порядка, к которому свёлся исходный определитель, будем вычислять тем же способом. Вычтем из второго и третьего столбцов первый столбец, умноженный соответственно на 2 и 7. Получим (попутно вынося общие множители из столбцов)

![]() ◄
◄
6) Используя метод приведения к треугольному виду вычислить определитель
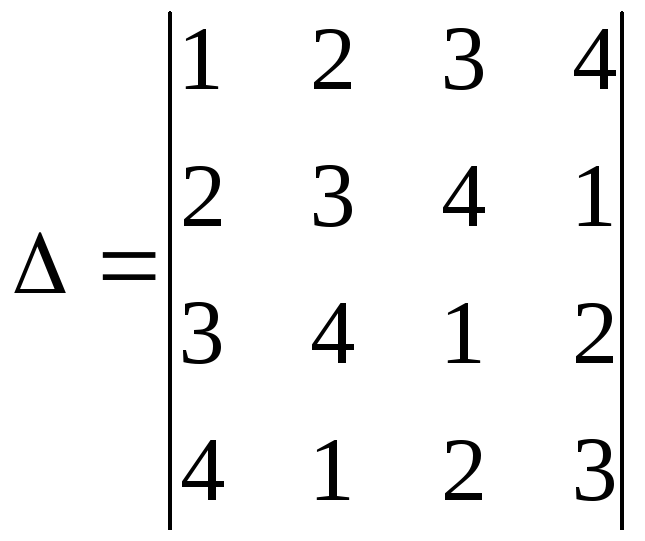
►Воспользуемся
видом определителя
![]() ,
который получился после процедуры
обращения в нуль всех элементов (кроме
первого) первой строки:
,
который получился после процедуры
обращения в нуль всех элементов (кроме
первого) первой строки:
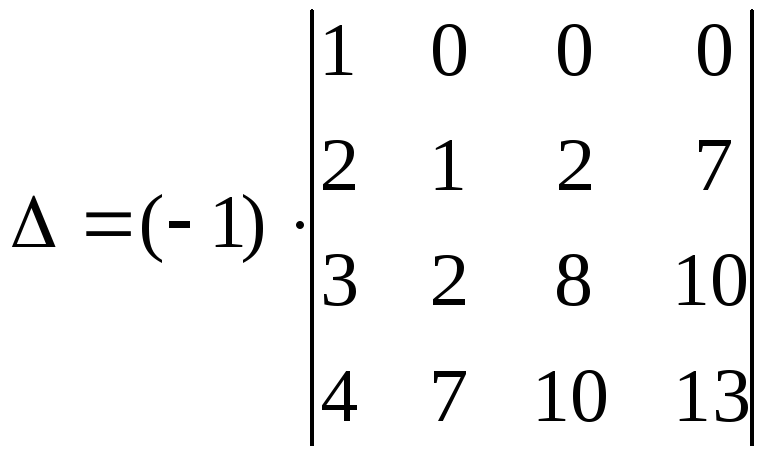 .
.
Далее с помощью второго столбца обратим в нуль элементы второй строки, кроме первых двух, для чего вычтем из третьего и четвёртого столбцов второй столбец, умноженный соответственно на 2 и 7. Получим (попутно вынося общие множители из столбцов)
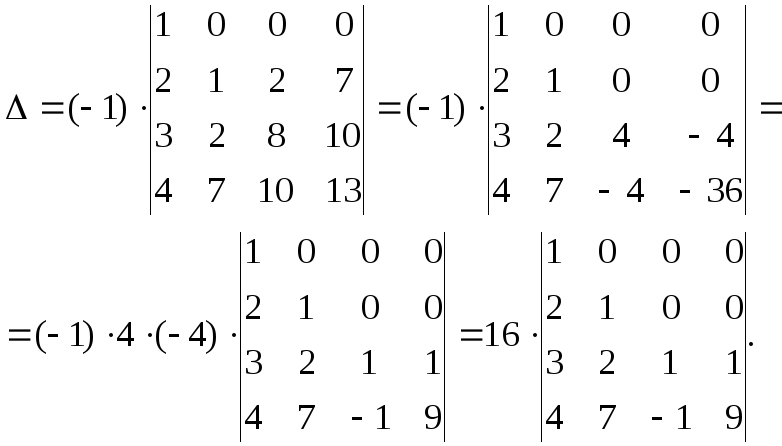
Наконец, вычтем третий столбец из четвёртого, в результате чего определитель сведётся к треугольному виду, величина которого равна произведению элементов главной диагонали:
 .◄
.◄

 ,
то
,
то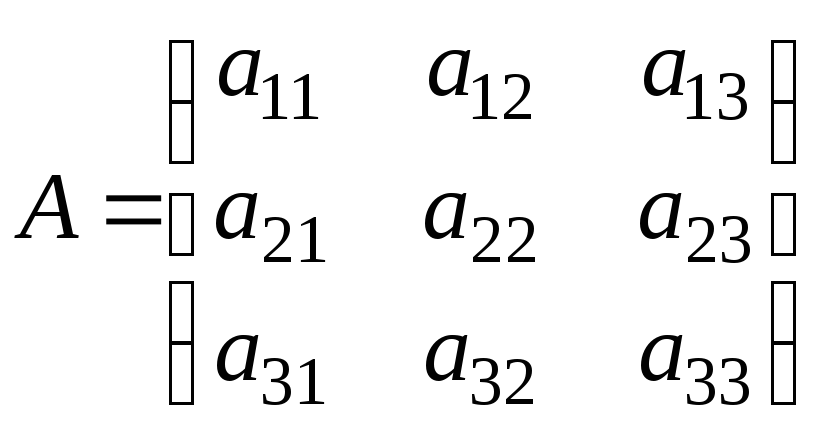 ,
то
,
то 