
- •Глава 1. Матрицы и определители
- •§1. Матрицы
- •1. Понятие матрицы
- •2. Квадратные матрицы
- •3. Действия с матрицами
- •Тогда суммарная производительность (за рабочий день) будет:
- •§2. Определители. Свойства. Вычисление
- •§3. Обратная матрица.
- •§4. Ранг матрицы
- •Идея практического метода вычисления ранга матрицы
- •Типовой пример. Найти ранг и указать какой-нибудь базисный минор матрицы .
- •Глава 2
- •§2. Решение линейных систем с помощью обратной матрицы. Правило Крамера. Теорема Кронекера-Капелли
- •§2. Метод Гаусса (метод последовательного исключения неизвестных) решения систем линейных уравнений
- •§4. Однородная система линейных алгебраических уравнений
- •Глава 3 линейные (векторные) пространства
- •§1. Понятие линейного пространства.
- •§ 2. Линейная зависимость и независимость систем векторов. Базис и размерность
- •Типовые примеры.
- •§ 3. Евклидовы пространства
- •Типовые примеры.
- •3.Матрица Грамма.Матрицей Грамадля системы векторовназывается симметричная матрица вида
- •4. Ортогональное разложение векторов. Говорят, что векторортогонален к подпространству, если векторортогонален любому вектору из этого подпространства.
- •§4.Унитарное пространство
- •§5. Определение линейного оператора. Матрица линейного оператора.
- •§ 5. Собственные векторы и собственные значения матриц.
- •§6. Симметрические операторы. Квадратичные формы и их применения
- •Типовые примеры.
§4.Унитарное пространство
Линейное
пространство
![]() называетсяунитарным
пространством,
если каждой паре
называетсяунитарным
пространством,
если каждой паре
![]()
![]() поставлено в соответствие комплексное
число, которое называется скалярным
произведением
поставлено в соответствие комплексное
число, которое называется скалярным
произведением![]() на
на![]() ,
обозначается
,
обозначается![]() ,
и для любых
,
и для любых![]()
![]() и комплексных
и комплексных![]() удовлетворяет следующим требованиям:
удовлетворяет следующим требованиям:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ,
причем равенство возможно лишь том
случае, когда
,
причем равенство возможно лишь том
случае, когда![]() .
.
Утверждение. Комплексное линейное пространство
Un=![]() ,
,
в котором скалярное произведение векторов задано равенством
![]() ,
,
является унитарным пространством.
Типовые примеры.
1.Векторы
![]() образуют ортонормированный базис в
унитарном пространстве. Найти скалярное
произведение
образуют ортонормированный базис в
унитарном пространстве. Найти скалярное
произведение![]() ,
если
,
если
![]() .
.
►В
рассматриваемом случае в соответствии
со свойствами скалярного произведения
в унитарном пространстве можно записать
![]() ◄
◄
2.В
унитарном пространстве со скалярным
произведением вида
![]() построить ортонормированный базис по
данному
построить ортонормированный базис по
данному
![]() .
.
►Сначала проведём процедуру ортогонализации. В данном случае она аналогична описанной для евклидова пространства. Положим
![]() .
.
Используя условия ортогональности, получим
 .
.
Теперь
отнормируем векторы
![]() :
:
 ◄
◄
§5. Определение линейного оператора. Матрица линейного оператора.
1.
Отображение
![]() из линейного пространства
из линейного пространства![]() в линейное пространство
в линейное пространство![]() называетсялинейным
отображением,
или линейным оператором, если для любых
векторов
называетсялинейным
отображением,
или линейным оператором, если для любых
векторов
![]() из
из![]() и любой константы
выполняются равенства:
и любой константы
выполняются равенства:
1)
![]()
2)![]()
Заметим,
что линейный оператор отображает нулевой
вектор в нулевой вектор. По свойству
линейности,
![]() .
.
Любая
матрица размера
![]() задаёт линейное отображение пространства
задаёт линейное отображение пространства![]() в пространство
в пространство![]() .
С другой стороны, любое линейное
отображениеL
конечномерных пространств можно задать
с помощью матрицы.
.
С другой стороны, любое линейное
отображениеL
конечномерных пространств можно задать
с помощью матрицы.
Представим
вектор x
в виде
![]() ,
где
,
где![]() - координаты,
- координаты,![]() -
базисные векторы, то по свойствам
оператора получим
-
базисные векторы, то по свойствам
оператора получим
![]()
![]()
![]() ,
откуда видно, что образ вектора зависит
лишь от координат этого самого вектора
и от того, куда отображаются оператором
n
базисных векторов пространства, то есть
зависит от векторов
,
откуда видно, что образ вектора зависит
лишь от координат этого самого вектора
и от того, куда отображаются оператором
n
базисных векторов пространства, то есть
зависит от векторов
![]() .
Матрица, составленная из этих векторов
(по столбцам), являетсяматрицей
линейного оператора.
.
Матрица, составленная из этих векторов
(по столбцам), являетсяматрицей
линейного оператора.
Замечание.
Рассмотрим линейный оператор, отображающий
векторы в пространстве![]() .
Этот оператор – знакомое ещё из школы
линейное отображение вида
.
Этот оператор – знакомое ещё из школы
линейное отображение вида![]() .
Причём коэффициент
.
Причём коэффициент![]() может рассматриваться в качестве матрицы
оператора (матрица порядка 1),x
– вектор в пространстве
может рассматриваться в качестве матрицы
оператора (матрица порядка 1),x
– вектор в пространстве
![]() .
Задать линейное отображение
.
Задать линейное отображение![]() на элементеx
= 1 достаточно, чтобы знать образ любого
числа x
при таком отображении. Фактически, здесь
число
на элементеx
= 1 достаточно, чтобы знать образ любого
числа x
при таком отображении. Фактически, здесь
число
![]() играет роль и матрицы размеров
играет роль и матрицы размеров![]() ,
и образа единицы:
,
и образа единицы:![]() .
.
2. Построение матрицы линейного оператора. Пусть отображение задано с помощью формулы
![]()
то
есть для координат произвольного
исходного вектора определены координаты
его образа. Тогда, рассматривая вместо
произвольного вектора x
вектор
![]() ,
найдём его образ, это будет вектор
,
найдём его образ, это будет вектор![]() .
Для этого в формуле, задающей образ
вектора, полагаем
.
Для этого в формуле, задающей образ
вектора, полагаем![]() ,
,![]() ,…,
,…,![]() .
Аналогично находим образы для
.
Аналогично находим образы для![]() ,…,
,…,![]() .
Из координат образа вектора
.
Из координат образа вектора![]() составляем 1-й столбец матрицы линейного
оператора, аналогично из координат
последующих векторов – остальные
столбцы. Рассмотрим на примере.
составляем 1-й столбец матрицы линейного
оператора, аналогично из координат
последующих векторов – остальные
столбцы. Рассмотрим на примере.
Пример. Пусть оператор задан с помощью формулы:
![]() .
.
►Прежде всего, докажем, что это отображение – действительно линейный оператор. Отобразим сумму векторов:
![]() .
Теперь каждую координату получившегося
вектора можем преобразовать:
.
Теперь каждую координату получившегося
вектора можем преобразовать:
![]()
![]()
![]()
![]() .
.
Аналогично для умножения на константу:
![]()
![]()
Для того чтобы найти матрицу этого линейного оператора, нужно, как было сказано выше, подставить значения x1=1, x2=0, а затем x1=0, x2=1. В этом примере образы базисных векторов – соответственно (3, 1) и (2, -1). Поэтому матрица линейного оператора будет иметь вид:
![]() .◄
.◄
Пример.
![]() .
.
►Построим матрицу оператора. Отображая вектор (1,0,0), получаем (1,4,-1), соответственно (0,1,0) переходит в (2,1,-2), а вектор (0,0,1) – в (-1,1,3). Матрица линейного оператора:
 .◄
.◄
Если
задана система
![]() изn
векторов, образующих базис, и какая-нибудь
произвольная система n
векторов
изn
векторов, образующих базис, и какая-нибудь
произвольная система n
векторов
![]() (возможно, линейно-зависимая), то
однозначно определён линейный оператор,
отображающий каждый вектор первой
системы в соответствующий вектор второй
системы.
(возможно, линейно-зависимая), то
однозначно определён линейный оператор,
отображающий каждый вектор первой
системы в соответствующий вектор второй
системы.
Матрицу этого оператора можно найти двумя способами: с помощью обратной матрицы и с помощью системы уравнений.
Пусть
![]() - матрица оператора в базисе
- матрица оператора в базисе![]() .
По условию,
.
По условию,![]() для всех индексов
для всех индексов![]() .
Данныеn
равенств можно записать в виде одного
матричного равенства:
.
Данныеn
равенств можно записать в виде одного
матричного равенства:
![]() ,
при этом столбцы матрицы
,
при этом столбцы матрицы![]() -
это векторы
-
это векторы![]() ,
а столбцы матрицы
,
а столбцы матрицы![]() - векторы
- векторы![]() .
Тогда матрица
.
Тогда матрица![]() может быть найдена в виде
может быть найдена в виде![]() .
.
Пример.
Найти матрицу
линейного оператора, отображающего
базис
![]() в систему векторов
в систему векторов![]() .
.
►Здесь
![]() ,
,![]() ,
,![]() ,
и получаем:
,
и получаем:
![]() .
.
Проверка
осуществляется умножением получившейся
матрицы на каждый вектор:
![]() .◄
.◄
Пример.
Линейными
операторами являются как правое, так и
левое векторное умножение на фиксированный
вектор в трёхмерном пространстве, то
есть отображения вида
![]() и
и![]() .
.
►Построим
матрицу одного из этих операторов,
![]() .Для
этого найдём образы всех трёх базисных
векторов линейного пространства.
.Для
этого найдём образы всех трёх базисных
векторов линейного пространства.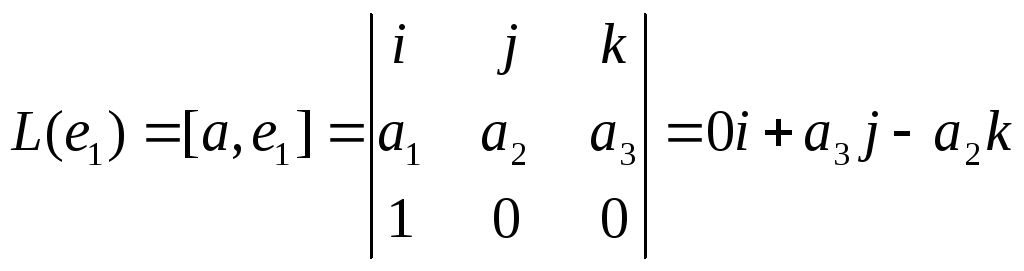 .
.
Аналогично,
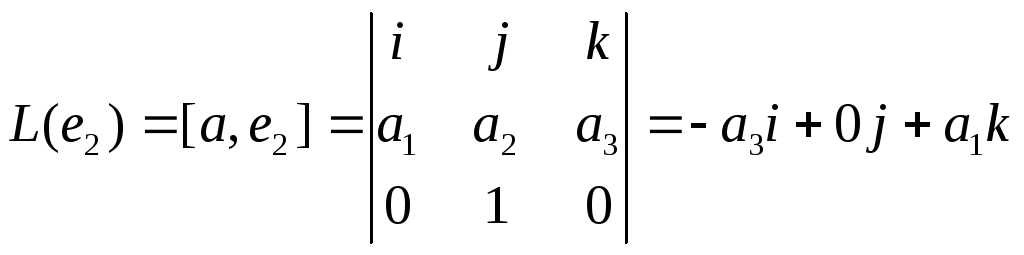 ,
,
 .
.
Координаты полученных векторов запишем в виде столбцов матрицы оператора.
Матрица
оператора:
 .
.
Аналогично
можно построить матрицу линейного
оператора
![]() :
:
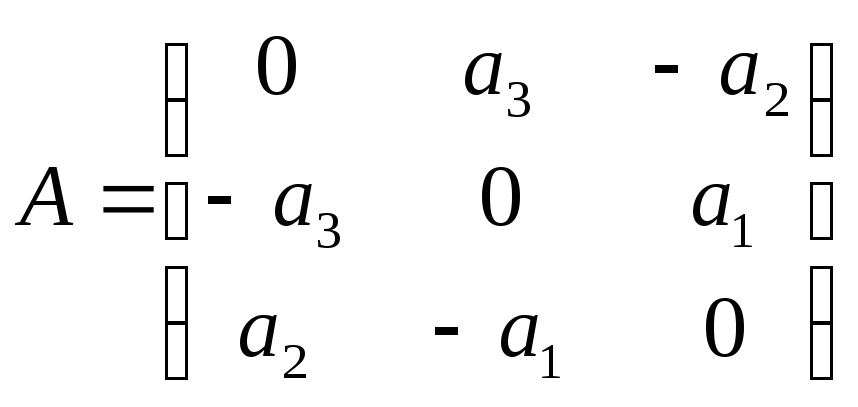 .◄
.◄
Пример.
Линейный оператор
дифференцирования в пространстве всех
многочленов степени не более n.
Это пространство размерности n+1.
Возьмём в качестве базиса элементы
![]() ,
,![]() ,
,![]() ,…,
,…,![]() .
.
►![]() ,
,
![]() ,
,![]() , аналогично получим
, аналогично получим![]() ,…,
,…,![]() .
.
Матрица этого линейного оператора:
 ◄
◄
3.
Сумма, произведение линейных операторов.
Для любых двух
линейных операторов
![]() определён
оператор
определён
оператор![]() ,
называемыйсуммой
данных двух
операторов. Действие оператора
,
называемыйсуммой
данных двух
операторов. Действие оператора
![]() на любой вектор пространства
на любой вектор пространства![]() определяется так:
определяется так:![]() .
.
Для
всякого линейного оператора
![]() определён оператор
определён оператор![]() ,
называемыйпроизведением
,
называемыйпроизведением
![]() на число
на число![]() .
Действие этого оператора задаётся с
помощью формулы
.
Действие этого оператора задаётся с
помощью формулы
![]() .
.
Для
линейных операторов
![]() ,
,![]() ,
определён оператор, называемыйкомпозицией
двух исходных
операторов и обозначаемый
,
определён оператор, называемыйкомпозицией
двух исходных
операторов и обозначаемый![]() .
Композиция определяется таким образом:
.
Композиция определяется таким образом:![]() .
.
