Формула Симпсона

Для вывода формулы Симпсона заменим подинтегральную функцию 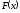на отрезке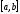некоторой вспомогательной функцией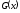. Пусть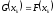для заданного равномерного разбиения

,

причем на частичных отрезках 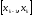функция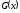является полиномом второй степени⁷.

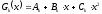Полиномы подберем так, чтобы выполнялись условия:

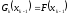, и.

В соответствии с выбором функции имеем, что искомый интеграл приблизительно равен интегралу от функции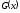. Зачем был сделан такой переход? Интеграл от полинома легко подсчитать...

.

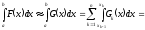
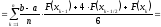
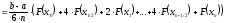Чтобы избегать работы с дробными индексами, решили ограничить значения nтолько четными числами и записывать формулу Симпсона в форме:

(2.9)

Примечание. Не следует забывать о важном ограничении формулы Симпсона - она работает только для четных n.

Погрешность 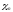формулы Симпсона удовлетворяет неравенству

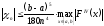(2.10)

при условии существования четвертой производной подинтегральной функции.

Выводы:

• Погрешность формулы Симпсона убывает как .

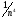• Формула Симпсона точнее формул прямоугольников и трапеций.

Пример. Сравнение формул при вычислении: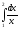

• Формула Ньютона - Лейбница: I= Ln(2) = 0.693147

• Формула Прямоугольников: I = 0.692835

• Формула Трапеций: I = 0.693771

• Формула Симпсона: I = 0.693150

На практике оценка погрешности численного интегрирования с помощью формулы (2.10) является малоэффективной из-за трудностей, связанных с оценкой производной .

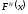Обычно поступают так - берут параметр n, кратный 4. Вычисляют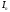и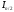. Тогда погрешность приблизительно равна⁸

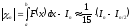. (2.11)

Алгоритм метода Симпсона похож на алгоритмы прямоугольников и трапеций. Просто при вычислении суммы элементов в круглых скобках (в цикле) следует поставить условие⁹: для четного номера точки разбиенияKзначение функции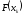следует умножить на 2, а для нечетного номера на 4.

Данные три метода - Симпсона, прямоугольников и трапеций - разработаны на основе геометрической интерпретации операции интегрирования, имеют простые алгоритмы и обладают важным свойством итерационных методов: изменяя некоторый параметр (количество точек разбиения), можно существенно повысить точность расчета. Их основной недостаток: если подинтегральная функция имеет сложный вид, то ее вычисление в десятках или сотнях точек может сильно замедлить работу программы¹⁰.

Ниже будут рассмотрены два метода приближенного интегрирования - формулы Чебышева и Гаусса. При выводе данных формул основное внимание было уделено именно скорости вычисления интеграла за счет понижения точности расчета (для некоторых классов функций). В этих методах требуется знать значение подинтегральной функции в 2 - 8 точках отрезка, но координаты этих точек выбираются строго определенным образом.

Квадратурная формула Чебышева

Рассмотрим квадратурную формулу

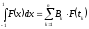. (2.12)

где 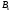- некоторые постоянные коэффициенты.

Ранее при вычислении приблизительного значения интеграла использовали равномерное распределение 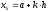. Чебышев предложил выбирать значения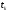иным образом, за счет чего удалось снизить количество расчетных точек при сохранении точности формулы.

Правила Чебышева:

• Коэффициенты 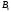равны между собой.

• Квадратурная формула (2.12) является точной для всех полиномов степени p, где.

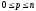Определим теперь конкретные значения коэффициентов Чебышева.

Т.к. 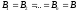, подставим в формулу (2.12) функцию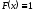. Получаем

.

Следовательно,

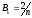. (2.13)

Для определения вспомним, что формула (2.12) точна для всех полиномов вида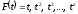. Подставив все вышеперечисленные полиномы в формулу (2.12), получим систему уравнений¹¹:

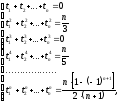(2.14)

Данная система при n<8илиn=9имеет единственное решение. При другихn, согласно С.Н. Берштейн, действительных решений не существует.

Решение системы (2.14) приведено в таблице:

n	k	tk	n	k	tk
2	1; 2	0.577350	5	1; 5 2; 4 3	0.832498 0.374541 0
3	1; 3 2	0.707107 0	6	1; 6 2; 5 3; 4	0.866247 0.422519 0.266635
4	1; 4 2; 3	0.794654 0.187592	7	1; 7 2; 6 3; 5 4	0.883862 0.529657 0.323912 0

Т.о. для отрезка интегрирования [-1,1]формула Чебышева имеет вид:

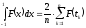. (2.15)

Чтобы применить квадратурную формулу Чебышева к интегралу типа

следует преобразовать его с помощью подстановки

,

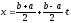переводящей отрезок 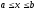в отрезок. Применяя к преобразованному интегралу формулу Чебышева, будем иметь

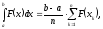(2.16)

где

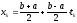. (2.17)

Следовательно, алгоритм формулы Чебышева можно представить следующим образом: Выбрать параметр n(чем больше, тем лучше). Задать с помощью констант значени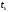яиз вышеприведенной таблицы. По формуле (2.17) вычислить значения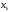. Далее можно вычислить приблизительное значение интеграла по формуле (2.16).

При использовании формулы Чебышева в программировании следует учитывать его важную характеристику: Интеграл от полинома определенной степени он вычисляет точно, но для всех других функций его погрешность может вырасти довольно сильно. Погрешность зависит от класса интегрируемой функции, от того, насколько точно ее можно приблизить полиномом.