Метод Ньютона

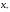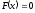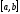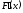Пусть корень уравненияявляется изолированным корнем на отрезке, причем первая производнаяи вторая производная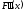непрерывны и сохраняют определенные знаки при.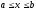

Если известно некоторое приближение решения 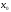, то его можно уточнить методом Ньютона.

Для вывода формулы метода Ньютона используем формулу Тейлора. Имеем

.

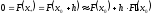Поэтому

.

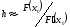Положим

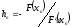(1.10)

и построим итерационный процесс

. (1.11)

Итак, метод Ньютона имеет следующую формулировку. Выберем начальное приближение . Найдем очередные приближения по формуле

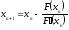, n=0,1,2... (1.12)

Критерии окончания расчетов для метода Ньютона аналогичны критериям метода итераций (приведены выше).

Теоретическое обоснование метода Ньютона заключено в следующей теореме.

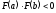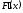Теорема. Если, причем первая производнаяи вторая производная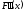непрерывны, отличны от нуля и сохраняют определенные знаки при, то, исходя из начального приближения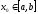, удовлетворяющего неравенству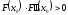, можно вычислить методом Ньютона корень уравнения с любой степенью точности.

Примечание. В качестве исходной точки 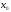можно выбрать тот конец интервала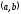, которому отвечает ордината того же знака, что и.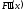

Примечание. Алгоритмы программ методов итераций и Ньютона практически совпадают, только очередные приближения 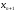вычисляются по разным формулам.

На практике для итерационных методов с первого раза трудно подобрать хорошее начальное приближение. Так, сходимость метода Ньютона сильно зависит от правильного выбора начального приближения. В случае его неверного выбора, ошибки в алгоритме или реализации неподходящего метода (у каждого метода есть свои определенные условия для решаемой задачи) программа обычно зацикливается или прекращает работу с ошибкой. Поэтому в программу для любого из итерационных методов рекомендуется вставить счетчик итераций,т.е. ввести специальную переменную. При вычислении очередного приближения (выполнена одна итерация) увеличивать значение этой переменной на единицу. Когда значение этой переменной превзойдет заранее заданное максимальное значение (для метода Ньютона обычно используют число 30), программа прекращает работу с выдачей соответствующего сообщения.

Пример. Ниже представлен фрагмент программы со счетчиком итераций Iter. Когда значение больше 30, программа прекращает свою работу.

{Задаем начальное значение счетчика итераций}

Iter:=0;

{начинаем цикл метода}

Repeat

{Вычисляем очередное приближение}

Xn1:=...

...

{Увеличиваем значение счетчика итераций}

Iter:=Iter+1;

{Если его значение превосходит максимально}

{заданное, даем сообщение и заканчиваем работу}

If Iter>30 then

begin

Writeln(’Корень уравнения не найден’);

Halt(1);

end;

{конец цикла и проверка критерия сходимости}

Until Abs(F(Xn1))<Eps;

Примечание. Метод Ньютона удобно применять в том случае, когда в окрестности корня график функции имеет большую кривизну (т.е. значение производной 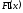велико). В противном случае метод сходится долго и его применение не рекомендуется.

приближения. Поэтому метод Ньютона при решении сложных прикладных задач используют в качестве второго дополнительного метода. Например, методом половинного деления находят приближенный корень с погрешностью 0.1, а затем методом Ньютона «уменьшают» погрешность до 0.0000001

Геометрический смысл метода Ньютона (см. рисунок № 2) заключается в замене кривой 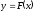касательной, проведенной в некоторой точке кривой. Выбирается начальное приближение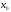. Проводится касательная к кривой в точке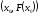. Абсцисса точки пересечения касательной и оси Ох берется за очередное приближение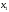. Далее снова проводится касательная в точке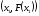и т.д. Из уравнения касательной и данного алгоритма можно также вывести формулу метода Ньютона.

Если на 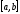существует изолированный корень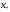с кратностьюp, то условие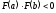может и не выполняться (при четной кратности). В этом случае, следует использовать вариант метода Ньютона с параметром для кратных корней:

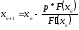. (1.15)