
2. Множини
Приклади розв’язання типових задач
Задача
1.
Нехай
![]() .
Визначити, які з наведених тверджень є
правильними, а які – ні. Відповідь
обґрунтувати.
.
Визначити, які з наведених тверджень є
правильними, а які – ні. Відповідь
обґрунтувати.
a)
![]() ; b)
; b)
![]() ; c)
; c)
![]() ;
;
d)
![]() ; e)
; e)
![]() ; f)
; f)
![]() .
.
Розв’язання.
Твердження
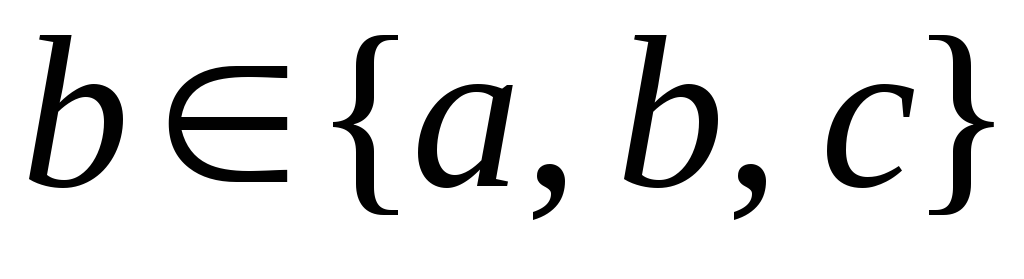 правильне,
тому що об’єкт
правильне,
тому що об’єкт
 міститься у множині
міститься у множині
 .
.Твердження
 також
правильне, оскільки множина
також
правильне, оскільки множина
 не
містить об’єкта
не
містить об’єкта
 .
.Твердження невірне, тому що серед елементів множини
 немає елемента.
немає елемента.Твердження правильне, оскільки для елементів множини
 маємо:
маємо: ,
отже,
,
отже,
 .
.Твердження
 невірне, оскільки елемент
невірне, оскільки елемент ,
але
,
але .
.Твердження вірне, оскільки множина не має елементів, тому умова
 не порушується для жодного
не порушується для жодного .
.
Задача
2.
Обчислити
наведені вирази при заданих множинах
![]() ,
,![]() ,
,![]() ,
,![]() та
та![]() .
.
a)
![]() ; b)
; b)
![]() ; c)
; c)
![]() ; d)
; d)
![]() ; e)
; e)
![]() .
.
Розв’язання.
Оскільки лише елементи 5 та 6 є спільними для множин
 та
та ,
то
,
то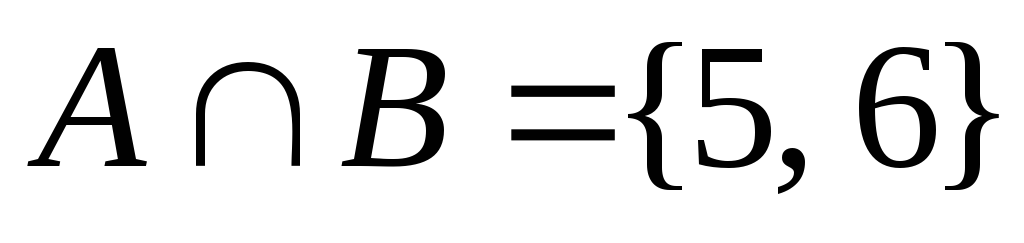 .
.Очевидно, не існує жодного елемента, який би належав як множині
 ,
так й множині
,
так й множині .
Отже, множина
.
Отже, множина
 не
містить жодного елемента, тобто є
порожньою:
не
містить жодного елемента, тобто є
порожньою:
 .
.
Елементи 2, 8, 0 належать множині
 і одночасно не належать множині
і одночасно не належать множині ,
тому
,
тому
 .
.Оскільки
 ,
то, скориставшись рівністю
,
то, скориставшись рівністю

 ,
маємо
,
маємо
 .
Ми отримали елементи, які належать або
тільки множині
.
Ми отримали елементи, які належать або
тільки множині
 ,
або тільки множині
,
або тільки множині ,
але не обом множинам
,
але не обом множинам та
та одночасно.
одночасно.Оскільки
 ,
то
,
то – множина елементів, які належать
універсальній множині
– множина елементів, які належать
універсальній множині і не належать множині
і не належать множині .
Остаточно,
.
Остаточно, .
.
Задача
3.
Довести,
що
![]() для будь-яких множин
для будь-яких множин
![]() і
і![]() .
.
Розв’язання.
Для доведення вказаної рівності достатньо
показати, що
![]() та
та
![]() .
Доведемо спочатку, що
.
Доведемо спочатку, що
![]() .
Використовуючи визначення операцій
різниці, перетину множин та операції
доповнення множини, маємо:
.
Використовуючи визначення операцій
різниці, перетину множин та операції
доповнення множини, маємо:
![]() та
та![]() та
та![]() ,
отже, доведено, що
,
отже, доведено, що![]() ,
а це означає, що
,
а це означає, що
![]() .
Тепер покажемо, що
.
Тепер покажемо, що
![]() :
:
![]() ,
отже,
,
отже,
![]() .
.
Задача
4.
Довести,
що з
![]() випливає
випливає![]() для будь-яких множин
для будь-яких множин![]() .
.
Розв’язання.
Потрібно показати, що
![]() за умови
за умови
![]() .
Іншими словами, при доведенні включення
.
Іншими словами, при доведенні включення
![]() можна користуватися не лише загальними
відомостями про множини (такими,
наприклад, як означення підмножини та
операцій над множинами), але й тим, що
можна користуватися не лише загальними
відомостями про множини (такими,
наприклад, як означення підмножини та
операцій над множинами), але й тим, що
![]() .
Отже, нехай
.
Отже, нехай
![]() .
Тоді, згідно з означенням операції
перетину множин, маємо:
.
Тоді, згідно з означенням операції
перетину множин, маємо:![]() та
та![]() .
Оскільки
.
Оскільки![]() ,
то з того, що
,
то з того, що![]() ,
випливає
,
випливає![]() .
Отже, з того, що
.
Отже, з того, що![]() та
та![]() ,
випливає
,
випливає![]() ,
тобто
,
тобто
![]() .
.
Задача
5.
Довести,
що
![]() для будь-яких множин
для будь-яких множин![]() .
.
Розв’язання.
Для доведення цієї еквівалентності
потрібно показати, що
![]() та
та![]() .
.
Доведемо
спочатку, перше з цих тверджень. Для
цього доведемо включення
![]() за умови, що
за умови, що ![]() .
Отже, нехай
.
Отже, нехай
![]() .
Звідси випливає, що
.
Звідси випливає, що
![]() та
та![]() (тобто
(тобто![]() ).
Оскільки
).
Оскільки![]() ,
то
,
то
![]() ,
отже,
,
отже,![]() або
або![]() .
Але відомо, що
.
Але відомо, що![]() ,
тобто залишається тільки можливість
,
тобто залишається тільки можливість![]() .
Таким чином, показано, що
.
Таким чином, показано, що![]() ,
а це означає, що
,
а це означає, що![]() .
.
Доведемо
друге твердження:
![]() .
Потрібно показати, що
.
Потрібно показати, що![]() за умови
за умови ![]() .
Нехай
.
Нехай
![]() .
Для довільної множини
.
Для довільної множини![]() або
або![]() ,
або
,
або![]() .
Розглянемо окремо кожен з цих випадків.
Нехай
.
Розглянемо окремо кожен з цих випадків.
Нехай![]() .
Тоді з означення операції об’єднання
множин випливає, що
.
Тоді з означення операції об’єднання
множин випливає, що![]() є елементом множини, яка є об’єднанням
множини
є елементом множини, яка є об’єднанням
множини![]() з будь-якою множиною. Отже,
з будь-якою множиною. Отже,![]() .
Розглянемо тепер другий випадок, тобто
.
Розглянемо тепер другий випадок, тобто![]() .
Тоді
.
Тоді![]() ,
а оскільки
,
а оскільки![]() ,
то
,
то![]() .
Але відомо, що
.
Але відомо, що![]() ,
а це означає, що
,
а це означає, що![]() ,
тобто
,
тобто![]() .
.
Доведення можна записати таким чином:
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() або
або
![]() ,
,![]()
![]()
![]() .
.
![]()
![]()
![]() ,
,
![]() або
або![]()
![]() 1)
1)
![]() ,
,![]() або 2)
або 2)![]() ,
,![]() .
.
1)
![]() ,
,![]()
![]()
![]()
![]()
![]() .
.
2)
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Задача
6.
Використовуючи
основні теореми та аксіоми алгебри
множин, довести, що
![]() .
.
Розв’язання.
Для спрощення виразу в лівій частині
рівності послідовно застосуємо закон
де Моргана, тотожність
![]() ,
закон асоціативності та закон
ідемпотентності
,
закон асоціативності та закон
ідемпотентності![]() :
:
![]() .
.
Задача
7.
Спростити
вираз
![]() .
.
Розв’язання. Маємо
![]()
![]() .
.
При
спрощенні даного виразу послідовно
застосовувалися закон дистрибутивності
(до виразу
![]() ),
тотожності
),
тотожності
![]() та
та
![]() .
При перетвореннях також використовувались
закони асоціативності та комутативності.
.
При перетвореннях також використовувались
закони асоціативності та комутативності.
Задача
8.
Нехай
![]() .
Побудувати
.
Побудувати![]() та
та![]() .
.
Розв’язання.
Декартовим добутком множин
![]() та
та![]() є множина
є множина
 .
.
Декартовим
степенем множини
![]() є множина
є множина

![]() .
.
Задача
9.
Довести,
що
![]() .
.
Розв’язання.
Доведемо спочатку, що
![]() .
Множина
.
Множина![]() є декартовим добутком двох множин
є декартовим добутком двох множин ![]() та
та
![]() ,
отже, елементи цієї множини – це
впорядковані пари. Таким чином, маємо:
,
отже, елементи цієї множини – це
впорядковані пари. Таким чином, маємо:![]() або
або![]() та
та![]() або
або![]() та
та![]()
![]() або
або![]() .
Це і означає, що
.
Це і означає, що![]() .
.
Тепер
покажемо, що
![]() .
Аналогічно попередньому випадку
.
Аналогічно попередньому випадку![]() або
або
![]()
![]() та
та![]() або
або![]() та
та![]() .
.
Розглянемо
випадок
![]() та
та![]() .
Маємо:
.
Маємо:![]() та
та![]()
![]()
![]() .
Якщо
.
Якщо
![]() та
та![]() ,
то маємо:
,
то маємо:![]() та
та![]()
![]() .
Отже,
у кожному випадку доведено, що
.
Отже,
у кожному випадку доведено, що
![]() .
Таким чином, рівність виконується.
.
Таким чином, рівність виконується.
A2
1. Задати
множину
![]() іншим способом:
іншим способом:
 –корінь
рівняння
–корінь
рівняння
 ;
;
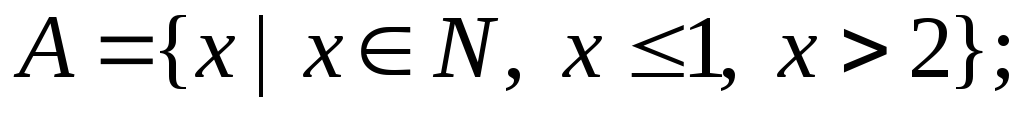
 ,
де
,
де
 .
.
2. Вказати вірні співвідношення:
1
 {1,
2, 3}; f)
1
{1,
2, 3}; f)
1 {1,
2, 3};
k)
0
{1,
2, 3};
k)
0 Ø;
Ø;1
 {{1,
2, 3}}; g)
{1}
{{1,
2, 3}}; g)
{1} {1,
2, 3};
l)
Ø
{1,
2, 3};
l)
Ø {Ø};
{Ø};{1}
 {1,
2, 3}; h)
{1}
{1,
2, 3}; h)
{1} {{1,
2, 3}};
m)
Ø
{{1,
2, 3}};
m)
Ø {1,
2};
{1,
2};{1}
 {{1},
{ 2, 3}};i)
{1}
{{1},
{ 2, 3}};i)
{1} {{1,
2}, 3}; n)
Ø
{{1,
2}, 3}; n)
Ø {Ø};
{Ø};1
 {{1},
{ 2}, 3};j)
{1, 2}
{{1},
{ 2}, 3};j)
{1, 2} {1,
2, 3}; o)
Ø
{1,
2, 3}; o)
Ø {1,
2}.
{1,
2}.
3. Вказати вірні співвідношення:
 c)
c)

 d)
d)

4.
Нехай
![]() –
довільні скінченні множини. Вказати
вірні твердження:
–
довільні скінченні множини. Вказати
вірні твердження:
 d)
d)

 e)
e)
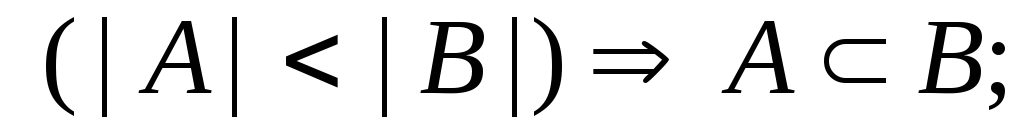
 f)
f)
 .
.Нехай
 –множина
всіх парних чисел,
–множина
всіх парних чисел,
 –
множина всіх чисел, які можуть бути
представлені у вигляді суми двох
непарних чисел. Довести, що
–
множина всіх чисел, які можуть бути
представлені у вигляді суми двох
непарних чисел. Довести, що

Побудувати булеан множини
 ,
тобто множину всіх її підмножин.
,
тобто множину всіх її підмножин.Яку кількість підмножин містить
порожня множина;
одноелементна множина;
двоелементна множина.
Зі скількох елементів складається множина
 ,
якщо її булеан містить 32 елементи?
,
якщо її булеан містить 32 елементи?Довести, що нескінченна множина має безліч підмножин.
Які з даних тверджень справедливі для будь-яких множин

а)
![]() і
і
![]()
b)
![]() і
і
![]() ?
?
Відповідь обґрунтувати.
Нехай
 ,
, ,
, .
Побудувати
.
Побудувати




 .
.Чи виконується для довільних множин
 і
і рівність
рівність ?Відповідь
обґрунтувати. Сформулювати і довести
необхідні та достатні умови виконання
цієї рівності.
?Відповідь
обґрунтувати. Сформулювати і довести
необхідні та достатні умови виконання
цієї рівності.Довести закон де Моргана

Довести включення
 .
.Довести еквівалентності:
a)
![]() ;
;
b)
![]() ;
;
c)
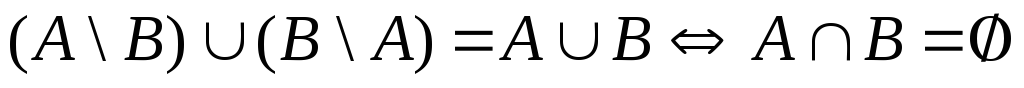 .
.
Перевірити (довести або спростувати) справедливість таких тверджень:
a)
якщо
![]() ,
то
,
то![]() ;
;
b)
якщо
![]() ,
то
,
то![]() ;
;
c)
якщо
![]() та
та![]() ,
то
,
то![]() .
.
За допомогою діаграм Венна перевірити теоретико-множинну рівність
 .
Довести
її двома способами.
.
Довести
її двома способами.Довести тотожності, використовуючи основні теореми та аксіоми алгебри множин:
a)
![]() ;
;
b)
 ;
;
c)
 .
.
Спростити вираз (
 – універсальна множина):
– універсальна множина):
a)
![]() ;
;
b)
![]() .
.
Побудувати приклади розбиття та покриття множини
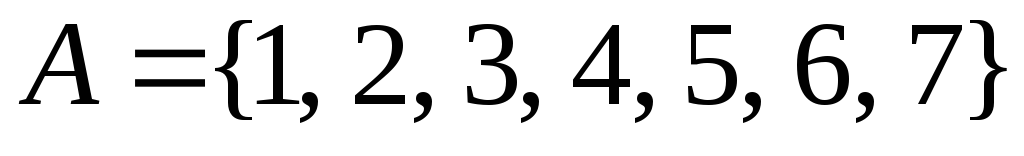 .
.Побудувати
 ,
якщо
,
якщо ,
, .
.Нехай
 – скінченні множини, причому
– скінченні множини, причому .
Скільки елементів містить множини
.
Скільки елементів містить множини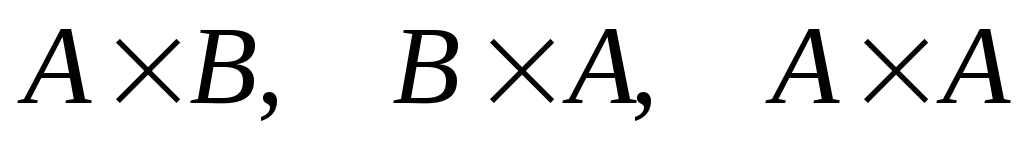 ?
?Що можна сказати про множини
 і
і ,
якщо:
,
якщо:
a)
![]() ; b)
; b)
![]() ?
?
Побудувати
 ,
якщо
,
якщо ,
, ,
, .
.Зобразити на площині такі множини:
a)
![]() ; b)
; b)
![]() .
.
Довести, що для довільних множин
 виконується
виконується
 .
.Довести, що для довільних непорожніх множин
 виконується
виконується
 і
і
 .
.
B2
Чи є множиною рівність:
а)
![]() ;
;
b)
![]() ;
;
с)
![]() ?
?
Множини задані за допомогою характеристичної властивості. Задати їх за допомогою переліку елементів:
a)
![]()
![]() ;
;
b)
![]() .
.
Множини задані переліком елементів. Записати їх за допомогою характеристичної властивості.
a)
![]()
b)
![]()
З яких елементів складається множина
 якщо
якщо ?
?Нехай
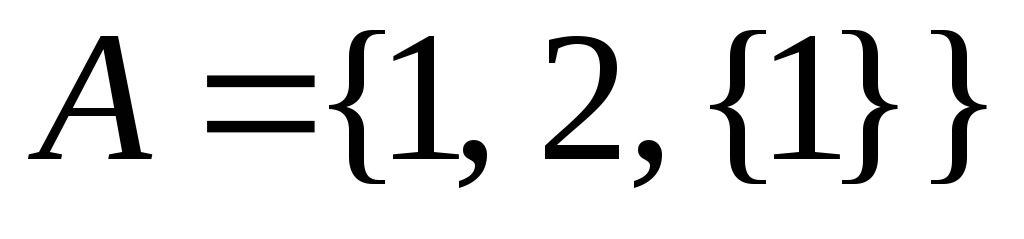 .
Навести декілька вірних співвідношень
із знаками належності та включення.
.
Навести декілька вірних співвідношень
із знаками належності та включення.Визначити всі можливі співвідношення (рівності, нерівності, включення, строге включення) між такими множинами геометричних фігур:
![]() –множина
всіх ромбів;
–множина
всіх ромбів;
![]() –множина
всіх ромбів, усі кути яких прямі;
–множина
всіх ромбів, усі кути яких прямі;
![]() –множина
всіх квадратів;
–множина
всіх квадратів;
![]() –множина
прямокутників, усі сторони яких рівні;
–множина
прямокутників, усі сторони яких рівні;
![]() –множина
всіх прямокутників;
–множина
всіх прямокутників;
![]() –множина
чотирикутників, усі кути яких прямі.
–множина
чотирикутників, усі кути яких прямі.
Чи існують такі множини
 та
та ,
що
,
що
 і
і
 ?
?Які з наведених тверджень є правильними (
 – множини):
– множини):
a)
якщо
![]() і
і
![]() то
то![]()
b)
якщо
![]() і
і
![]() то
то![]()
У тих випадках, коли твердження невірне, разом із контрприкладами побудуйте окремі приклади, для яких воно виконується.
Для заданої множини
 побудувати множину всіх підмножин
побудувати множину всіх підмножин
 Ø; b)
Ø; b)
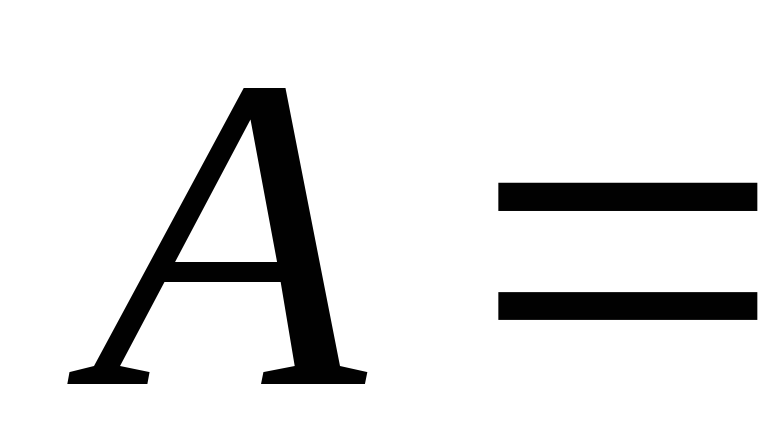 {Ø};
c)
{Ø};
c)
 .
.Маючи множини
 ,
за допомогою операцій
,
за допомогою операцій та доповнення записати множини
елементів, які
та доповнення записати множини
елементів, які
належать всім трьом множинам;
належать принаймні двом з даних множин;
належать хоча б одній з цих множин;
не належать будь-яким двом множинам, але належать хоча б одній з них;
не належать жодній із множин.
Нехай
 – множина
всіх прямокутників,
– множина
всіх прямокутників,
 –
множина всіх ромбів на площині. З яких
елементів складається множина
–
множина всіх ромбів на площині. З яких
елементів складається множина
a)
![]() ; b)
; b)
![]() ;
c)
;
c)
![]() ?
?
Нехай
 Обчислити
Обчислити
a)
![]() ; b)
; b)
![]() ;
c)
;
c)

Що можна сказати про множини
 і
і ,
якщо:
,
якщо:а)
 ;
;b)
 ;
;c)
 ;
;d)
 ;
;e)
 ;
;f)
 ;
;g)
 ;
;h)
 ;
;i)
 .
.Знайти множини
 та
та ,
якщо
,
якщо і
і
Довести еквівалентності:
a)
![]() і
і![]() ; b)
; b)
![]() .
.
Довести один із законів поглинання.
За допомогою діаграм Венна перевірити такі рівності:
a)
![]() ; b)
; b) .
.
Довести тотожності шляхом рівносильних перетворень.
а)
 ; d)
; d)
![]() ;
;
b)
 ; e)
; e)
 .
.
c)
 ;
;
Спростити вирази:
a)
![]() ;
;
b)
![]() ;
;
с)
![]() .
.
Знайти всі розбиття множини
 .
.Із вказаних нижче множин підібрати такі їх системи, які задавали б розбиття множини всіх цілих чисел
 :
:
![]() ;
;
![]() ;
;
![]() –множина
всіх цілих додатних чисел;
–множина
всіх цілих додатних чисел;
![]() –множина
всіх цілих від’ємних чисел;
–множина
всіх цілих від’ємних чисел;
![]() –множина
всіх парних чисел;
–множина
всіх парних чисел;
![]() –множина
всіх непарних чисел;
–множина
всіх непарних чисел;
![]() –множина
всіх простих чисел;
–множина
всіх простих чисел;
![]() –множина
всіх складених натуральних чисел.
–множина
всіх складених натуральних чисел.
Навести
два приклади покриття множини
![]() .
.
Побудувати
 ,
якщо
,
якщо ,
, ,
, .
.Побудувати
 ,
якщо
,
якщо .
.Коли в множині
 є хоча б один елемент з однаковими
першою та другою координатами?
є хоча б один елемент з однаковими
першою та другою координатами?Довести тотожність
 ,
де
,
де – непорожні множини.
– непорожні множини.Довести, що для довільних непорожніх множин
 виконується твердження
виконується твердження .
.
С2
Чи існують такі множини
 ,
для яких виконувалися б умови:
,
для яких виконувалися б умови:
a)
![]() ;
;
b)
![]() .
.
Нехай
 – довільна множина. Обчислити:
– довільна множина. Обчислити:
a)
![]() ; d)
; d)![]() ; g)
; g)![]() ;
;
b)
![]() ; e)
; e)![]() ; h)
; h)![]() ;
;
c)
![]() ; f)
; f)![]() ; i)
; i)![]() .
.
Обчислити:
a)
![]() ;c)
;c)
![]() ;e)
;e)
![]() ;
;
b)
![]() ;d)
;d)
![]() ; f)
; f)
![]() .
.
Нехай
 – скінченні
множини,
– скінченні
множини,
 ,
,
 .
Обчислити
.
Обчислити .
.На фірмі працюють 67 чоловік. З них 47 співробітників володіють англійською мовою, 35 – німецькою, 23 володіють обома мовами. Скільки співробітників фірми не знають жодної іноземної мови?
Довести узагальнені закони:
a)
![]() ;
;
b)
![]() .
.
Спростити
a)
![]() ;
;
b)
![]() .
.
Довести тотожності:
a)
![]() ;
;
b)
![]() ;
;
с)
 ;
;
d)
![]() .
.
Довести
 ,
де
,
де – булеани множин
– булеани множин та
та відповідно.
відповідно.Яким повинно бути розбиття скінченної множини
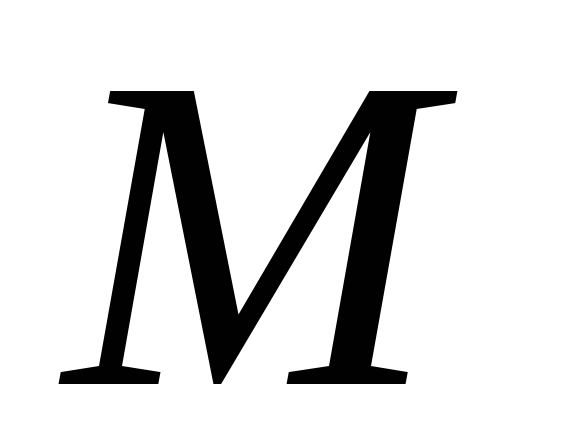 на два класи
на два класи ,
щоб декартів добуток
,
щоб декартів добуток містив найбільшу кількість елементів?
містив найбільшу кількість елементів?Чи істинними будуть твердження:
a)
![]() ; b)
; b)
![]() ; с)
; с)
 Ø.
Ø.
