
Спецглавы
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
™КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени Т. Ф. Горбачева®
Кафедра математики
СПЕЦГЛАВЫ МАТЕМАТИКИ
Методические указания к контрольной работе для студентов направления подготовки 140100.62 ™Теплоэнергетика
и теплотехника® заочной формы обучения
Составители И. А. Ермакова Г. А. Липина
Г. В. Алексеевская
Утверждены на заседании кафедры Протокол № 3 от 04.12.2012 Рекомендованы к печати учебно-методической комиссией направления 140100.62 Протокол № 6 от 05.12.2012 Электронная копия находится в библиотеке КузГТУ
Кемерово 2012
1
Дисциплина ™Специальные главы математики® включает в себя три раздела:
1)элементы теории множеств;
2)элементы математической логики;
3)элементы теории графов.
Студент выполняет контрольную работу, выбирая вариант задания по последней цифре зачетной книжки. Если последняя цифра равна 0, то студент решает вариант №10. Работа, выполненная не по своему варианту, не проверяется.
ПРОГРАММА КУРСА 1. Элементы теории множеств
1.1.Общие понятия теории множеств
1.2.Операции над множествами
2. Элементы математической логики
2.1.Общие понятия
2.2.Виды логических операций
2.3.Формализация сложных высказываний
2.4.Нахождение значений простых высказываний, входящих в
сложное
2.5.Логическая равносильность
3. Элементы теории графов
3.1.Основные понятия
3.2.Степень вершины
3.3.Маршруты, цепи, циклы
3.4.Связность графа
3.5.Ориентированные графы
3.6.Способы задания графов, матрицы смежности и инцидентности
2
1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
1. Общие понятия теории множеств
Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно было введено в
математику немецким ученым Георгом Кантором (1845 1918). Множество – совокупность объектов, обладающих определенным свойством, объединенных в единое целое. Например, множество студентов в группе, множество целых чисел и т. д.
Элементами множества называются объекты, его составляющие. Множества обозначаются прописными буквами латинского алфавита: A, B, C,... а элементы множеств – строчными буквами: a, b, c,… .
Запись a M означает: элемент a принадлежит множеству M. Аналогично a M читаем как: элемент a не принадлежит множеству M. Термин ™множество® употребляется независимо от того, сколько в этом множестве элементов. Множество, не содержащее ни одного элемента, называется пустым и обозначается символом . Примеры пустых множеств:
а) множество треугольников, сумма углов которых больше
1800;
б) множество отрицательных чисел, являющихся решением неравенства 2<x<10.
Мощностью множества A называется число элементов этого множества, обозначается |A| или n(A). Мощность пустого множества равна нулю: n( ) = 0.
Способы задания множеств: перечисление и описание его элементов. Перечисление состоит в получении полного списка элементов множества. Описание заключается в задании такого свойства, которым элементы данного множества обладают, а все остальные нет.
Конечные множества можно задавать обоими способами, причем выбор того или иного способа зависит от удобства задания и дальнейшей работы с множеством. Бесконечные множества можно задавать только с помощью описания.
Множество |
объектов |
x, |
обладающих |
свойством A(x), |
|||
обозначается |
x |
|
A x . |
При |
этом, |
A(x) |
называется |
|
|||||||
3
характеристическим свойством множества.
Пример 1:
а) Задать множество четных чисел, удовлетворяющих
неравенству 1 x 5. |
Первый способ: A 2, 4 . Второй способ: |
|||||
A x |
|
|
1 x 5 и x четное |
|
|
|
|
|
|
||||
б) |
Перечислить |
элементы множества B x |
|
x N , x 5 . |
||
|
||||||
Запись означает, что все элементы множества В обладают общими свойствами: принадлежат множеству натуральных чисел N и меньше 5. Таким образом, B 1, 2, 3, 4 .
Равенство двух множеств А и В А В означает, что они состоят из одних и тех же элементов.
Универсальным называют множество U, состоящее из всех
возможных |
элементов, |
обладающих |
данным |
признаком. |
Например, |
U – множество планет |
Солнечной |
системы: |
|
Земля, Марс, Меркурий, Венера, Уран, Юпитер, Нептун, |
||||
U |
|
|
|
|
Плутон, Сатурн |
|
|
|
|
Подмножеством А |
множества |
В является |
любая часть |
|
множества В. Например:
а) множество жителей Кузбасса (А) является подмножеством множества жителей России (В);
б) множество четных чисел (А) является подмножеством множества целых чисел (В).
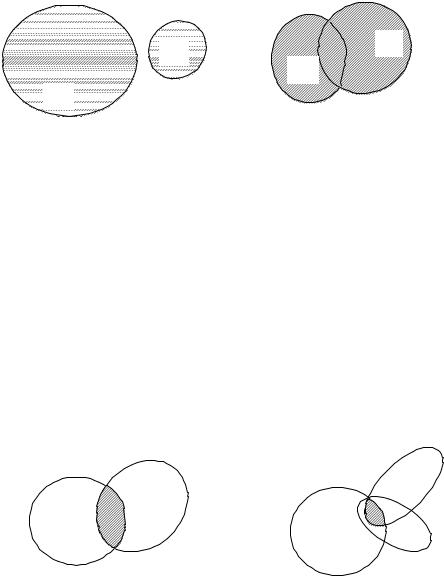
Таким образом, если А есть подмножество В, то A B . Наглядно соотношения между множествами иллюстрируются с помощью диаграмм Венна. Диаграмма Венна – это замкнутая линия, внутри которой расположены элементы данного множества, а снаружи – элементы, не принадлежащие этому множеству (рис.1.1).
В |
А |
Рис.1.1. Отношение A B
4
1.2. Операции над множествами
1.2.1. Объединением С двух множеств А и В называется множество, состоящее из всех элементов, принадлежащих или множеству А, или множеству В, или обоим множествам вместе. Обозначение: C A B . Объединение множеств также называют суммой множеств. Объединение трех и более множеств определяется аналогично.
Пример 2. Изобразить штриховкой объединение множеств (рис.1.2):
а) А 1, 2, 3, 4 и В 6, 7 ; A B 1, 2, 3, 4, 6, 7
б) С 1, 2, 3 и D 2, 3, 4, 5 ; С D 1, 2, 3, 4, 5
а) |
б) |
В |
D |
|
С |
||
|
А
Рис.1.2. Объединение множеств: а) A B , б) С D
1.2.2. Пересечением С двух множеств А и В называется множество, состоящее из элементов, принадлежащих и множеству А, и множеству В одновременно. Обозначение: C A B . Пересечение образовано всеми общими элементами данных множеств. Пересечение трех и более множеств определяется аналогично.
Пример 3. Изобразить штриховкой пересечение множеств
(рис.1.3): |
|
|
а) А 1, 2, 3 и В 2, 3, 4, 5 ; А В 2, 3 |
|
|
б) С 1, 2, 3, 4 и D 4,5, 6, 7 ; E 3, 4,5 , |
C D E 4 |
|
а) |
б) |
|
|
В |
D |
А |
E |
|
С |
||
|
Рис.1.3. Пересечение множеств: а) A B , б) C D E

5
1.2.3. Разностью С двух множеств А и В называют множество, состоящее из всех элементов А, не входящих в В. Обозначение: C A\ B (™С равно А без В®). Таким образом, из множества А достаточно удалить общие элементы множеств А и В.
Пример 4. Изобразить штриховкой разность множеств (рис.1.4):
а) А 1, 2, 3 и В 2, 3, 4, 5 ; А\ В 1 б) А 1, 2, 3, 4 и В 3, 4 ; А\ В 1, 2 в) А 1, 2, 3 , В 4, 5 ; А\ В 1, 2, 3
а) |
б) |
в) |
|
А |
В |
А |
В |
А |
|||
|
|
В |
|
Рис.1.4. Разность множеств A\ B
1.2.4. Дополнением к множеству А называется множество элементов, которые не принадлежат А, и дополняют его до универсального множества U. Обозначается: A .
Пример 5. Изобразить штриховкой дополнение множества А (рис.1.5):
а) А 1, 2, 3 , U 2, 3, 4, 5 ; А U\A 4, 5 .
U
|
|
|
|
|
А |
|
|
|
|
|
Рис.1.5. Дополнение множества А |
||||
ЗАДАНИЕ 1. |
U 1, 2, 3, 4, 5, 6, 7 – |
|
|||||
Заданы |
множества: |
универсальное, |
|||||
A 2, 4, 7 , |
B 1,3,5, 7 , |
C 2,3,5, 6 . Перечислить элементы |
|||||
множества M |
|
B A . |
|
||||
C |
|
||||||
Для нахождения множества М выполним |
операции над |
||||||
множествами в следующем порядке: |
|
||||||

6
1) Найдем дополнение:
CU \ C 1, 2, 3, 4, 5, 6, 7 \ 2,3, 5, 6 1, 4, 7 . 2) Найдем пересечение двух множеств:
CB 1, 4, 7 1,3, 5, 7 1, 7 .
3) Найдем объединение двух множеств:C B A 1, 7 2, 4, 7 1, 2, 4, 7 . Отсюда М C B A 1, 2, 4, 7 .
2. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
2.1. Общие понятия
Логика – наука о законах мышления и его формах.
Законы мышления – это правила, соблюдение которых приводят рассуждения к истинным выводам.
Формы мышления характеризуют структурное строение высказываемых мыслей. Основные формы мышления включают в себя понятия, суждения (высказывания) и умозаключения.
Понятие — это форма мышления, в которой отражаются общие и существенные свойства (признаки) объектов и явлений. Признаки являются общими, если присущи всем объектам. Признаки являются существенными, если без них объект теряет свою суть.
Пример 6.
Понятие ™студент® может характеризоваться следующими признаками:
1)молодой человек;
2)учится в КузГТУ;
3)живет в общежитии;
4)учится в техникуме;
5)учится в техникуме или вузе.
Из перечисленных признаков общим и существенным является последний, так как остальные признаки могут не наблюдаться.
Суждение (высказывание) представляет собой форму мышления, в которой что-либо утверждается или отрицается о предметах, их свойствах, отношениях между ними.
Суждением является любое повествовательное предложение, про которое однозначно известно: истинно оно или ложно.
7
Простое суждение включает в себя:
1)субъект S (логическое подлежащее) – это понятие, о котором идее речь в суждении;
2)предикат Р (логическое сказуемое) – это понятие, с помощью которого что-либо утверждается или отрицается о субъекте;
3)связка – слова: ™есть®, ™является®, ™называется® и т.п. Связка в суждении может отсутствовать.
Пример 7.
Дано суждение: ™КузГТУ является старейшим вузом Кузбасса®.
Здесь субъект S – ™КузГТУ®, предикат Р – ™старейший вуз Кузбасса®, связка – слово ™является®. Суждение простое, утвердительное.
Пример 8.
Дано суждение: ™КузГТУ не имеет юридического факультета®. Здесь субъект S – ™КузГТУ®, предикат Р – ™имеет юридический факультет®, связка отсутствует, имеется частица ™не®. Суждение простое, отрицательное.
Простые суждения обозначаются латинскими буквами: p, q,…A, B, C, … X, Y…
Если высказывание p истинно, то записывают р 1. Если высказывание p ложно, то записывают р 0 .
Сложное суждение (высказывание) составляют из простых с помощью логических операций.
2.2. Виды логических операций
2.2.1. Отрицание – сложное высказывание, которое образуется из простого с помощью связок: ™не® или ™неверно, что®. Обозначается – р , читается – ™не р®.
Пример 9.
Дано простое высказывание p: ™КузГТУ является старейшим вузом Кузбасса®. Высказывание истинно, р 1.
Составим отрицание р : ™КузГТУ не является старейшим вузом Кузбасса® или ™Неверно, что КузГТУ является старейшим вузом Кузбасса®. Полученное высказывание ложно, р 0 .

8
Если изначальное простое высказывание ложно, то его отрицание будет истинно.
Пусть p: ™КузГТУ имеет юридический факультет®, р 0 . Тогда р : ™Неверно, что КузГТУ имеет юридический факультет®, р 1.
Запишем таблицу истинности для отрицания:
рр
1 0
01
Таблица истинности показывает возможные логические значения входящих простых высказываний и соответствующие значения сложных суждений (1 – истинно, 0 – ложно).
2.2.2. Конъюнкция (логическое умножение) – сложное высказывание, которое образуется из простых с помощью союзов ™и®, ™также®, ™и……, и…®. Обозначается p q , читается ™p и q®. Простые высказывания описывают некоторые события. Конъюнкция двух высказываний обозначает, что оба события происходят вместе; и первое, и второе одновременно.
Пример 10.
Запишем простые высказывания и составим из них конъюнкцию. При этом возможны следующие варианты.
1) Простые высказывания истинны:
р: ™При поступлении в КузГТУ сдают математику®, р 1; q: ™При поступлении в КузГТУ сдают физику®, q 1.
Сложное высказывание: ™При поступлении в КузГТУ сдают математику и физику® также является истинным, p q 1.
2) Одно (любое) из простых высказываний ложно: р: ™При поступлении в КузГТУ сдают математику®, р 1 q: ™При поступлении в КузГТУ сдают биологию®, q 0 .
Сложное высказывание: ™При поступлении в КузГТУ сдают математику и биологию® является ложным, p q 0 .
3) Оба простых высказываний ложны:
р: ™При поступлении в КузГТУ сдают физкультуру®, р 0 q: ™При поступлении в КузГТУ сдают биологию®, q 0 .
Сложное высказывание: ™При поступлении в КузГТУ сдают физкультуру и биологию® является ложным, p q 0 .
9
Таблица истинности для конъюнкции:
р |
q |
p q |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
Конъюнкция является истинной только тогда, когда оба исходных высказывания истинны. Если хотя бы одно из составляющих высказываний ложно, то и полученное из них с помощью союза ™и® сложное высказывание также считается ложным.
2.2.3. Дизъюнкция (логическое сложение) – сложное высказывание, которое образуется из простых с помощью союзов ™или®. Обозначается p q , читается ™p или q®. Дизъюнкция двух высказываний о некоторых событиях обозначает, что происходит или одно событие, или второе, или оба вместе.
Пример 11.
Запишем простые высказывания и составим из них дизъюнкцию. При этом возможны следующие варианты.
1) Простые высказывания истинны: р: ™В столовой куплю пиццу®, р 1;
q: ™В столовой куплю булочку®, q 1.
Сложное высказывание: ™В столовой куплю пиццу или булочку® также является истинным, p q 1.
2) Одно (любое) из простых высказываний ложно: р: ™В столовой куплю булочку®, р 1
q: ™В столовой куплю ручку®, q 0 .
Сложное высказывание: ™В столовой куплю булочку или ручку® является истинным, p q 1.
3) Оба простых высказываний ложны: р: ™В столовой куплю ручку®, р 0
q: ™В столовой куплю карандаш®, q 0 .
Сложное высказывание: ™В столовой куплю ручку или карандаш® является ложным, p q 0 .
