
Спецглавы
.pdf
20
определении оптимальной загрузки производственных элементов и обеспечивающих эту загрузку потоков.
3.Обменные схемы, являющиеся моделями таких явлений как бартер, взаимозачёты и т. д. Вершины графа при этом описывают участников обменной схемы (цепочки), а дуги – потоки материальных
ифинансовых ресурсов между ними. Задача заключается в определении цепочки обменов, оптимальной с точки зрения, например, организатора обмена и согласованной с интересами участников цепочки и существующими ограничениями.
4.Управление проектами. С точки зрения теории графов – совокупность операций и зависимостей между ними (сетевой график). Примером является проект строительства некоторого объекта. Совокупность моделей и методов, использующих язык и результаты теории графов и ориентированных на решение задач управления проектами, получила название календарно-сетевого планирования и управления (КСПУ). В рамка КСПУ решаются задачи определения последовательности выполнения операций и распределения ресурсов между ними, оптимальных с точки зрения тех или иных критериев (времени выполнения проекта, затрат риска и др.).
5.Модели коллектива и групп, используемые в социологии, основываются на представлении людей или их групп в виде вершин, а отношений между ними (например, отношений знакомства, доверия, симпатии и т. д.) – в виде рёбер или дуг. Тем самым решаются задачи исследования структуры социальных групп, их сравнения и т. д.
6.Модели организационных структур, в которых вершинами являются элементы организационной системы, а рёбрами или дугами
– связи (информационные, управляющие, технологические и др.) между ними.
Графом называется непустое конечное множество вершин V и множество ребер E, оба конца которых принадлежат множеству V.
Обозначение графа: G V, E  V , E
V , E  .
.
Изолированными вершинами, называются те, которые не принадлежат ни одному ребру. Обозначение вершин: V1, V2, ….Vn .
Пусть вершины V1 |
, V2 соединены ребром, это ребро |
обозначается: e V1,V2 . |
Тогда вершина V1 и ребро e |
инцидентны. Вершина V2 и ребро e тоже инцидентны. Два ребра, инцидентные одной вершине, называются смежными. Две вершины, инцидентные одному ребру, также называются
21
смежными.
Число вершин графа G обозначим p, а число ребер – q, то есть p: p G V ; q: q G E .
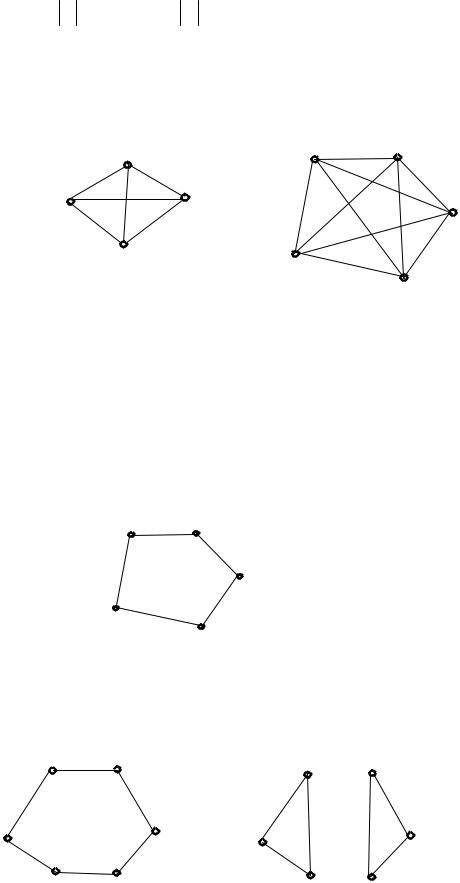
Граф называется полным, если каждые две различные вершины его соединены одним и только одним ребром (рис. 1.2).
V2 |
V2 |
V3 |
V1 |
V3 |
V4 |
|
|
|
V4 |
V1 |
|
|
Рис.3.2. Полные графы |
V5 |
|
|
Пример 19.
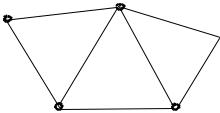
Утверждают, что в одной компании из пяти человек каждый знаком с двумя и только двумя другими. Возможна ли такая компания?
Каждого члена этой компании изобразим кружком. Если двое знакомы, соединим соответствующие кружки отрезками. Как видно из рисунка, такая компания возможна.
Пример 20.
Может ли так случиться, что в одной компании из шести человек каждый знаком с двумя и только с двумя другими?
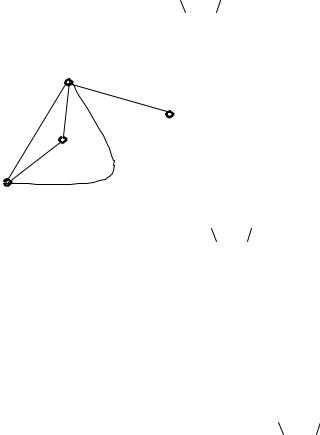
Изобразим графы, которые могут соответствовать такой компании.
G1 |
G2 |
22
Граф G1 является связным. В этом случае каждый человек через своих знакомых может познакомиться со всеми остальными. Граф G2 несвязный, он соответствует двум компаниям, участники одной из них незнакомы с участниками другой.
3.2. Степень вершины
Вершины могут принадлежать различному числу ребер, и в этом их отличие.
Степенью вершины называется число ребер графа, которым принадлежит эта вершина.
Степень вершины графа еще называют ее валентностью и обозначают d(V). Вершина графа называется изолированной, если она не имеет ребер, то есть d V 0 . Вершина называется висячей, если она принадлежит одному ребру, то есть d V 1.
Пример 21.
На рис.3.3 изображен граф G V, E  5, 5
5, 5 . Найти степени всех его вершин.
. Найти степени всех его вершин.
V3
V1 
V5
V4
V2
Рис.3.3. Граф G V, E  5, 5
5, 5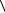
Подсчитаем количество ребер, которым принадлежит каждая вершина графа, получаем: d V1 0 , V1 – изолированная вершина;
d V2 3; d V3 4 ; d V4 2 ; d V5 1; V5 – висячая вершина. Вершина называется нечетной, если d V равно нечетному
числу. Вершина называется четной, если d V – четное число. В задаче 1 вершины V2 и V5 – нечетные, вершина V4 – четная.
На рис. 3.4 изображен полный граф G V, E  4, 6
4, 6 . То есть,
. То есть,
имеется 4 вершины, каждая из которых соединена с тремя другими вершинами. Степень каждой его вершины равна 3. Таким образом, степень каждой вершины полного графа на единицу меньше числа его
23
вершин.
V2
V1 
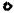 V3
V3
V4
Рис. 3.4. Полный граф G V, E  4, 6
4, 6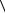
Сумма степеней всех вершин графа: 3 4 12 . Число ребер в данном графе равно 6, оно равно половине этой суммы.
В любом графе G V, E сумма степеней всех его вершин равна удвоенному числу ребер графа, есть число четное.
Число нечетных вершин любого графа есть число четное.
Во всяком графе с n вершинами, где n 2, найдутся по крайней мере две вершины с одинаковыми степенями. Если в графе с n вершинами (n 2) в точности две вершины имеют одинаковую степень, то в этом графе всегда найдется либо в точности одна вершина степени 0, либо в точности одна вершина степени n = 1.
Пример 22.
В офисе 15 работников, которым нужен телефон. Можно ли проложить телефонную сеть таким образом, чтобы каждый телефон был соединен ровно с пятью другими?
Для решения задачи предположим, что это возможно. Рассмотрим граф, вершины которого соответствуют телефонам, а ребра – соединяющим их проводам. В этом графе 15 вершин,
степень |
каждой вершины равна 5. |
Сумма степеней всех |
вершин |
равна: 15 5 75. Тогда число |
ребер: 75 / 2 37,5, равно |
нецелому числу. Значит, такого графа не существует, соединить телефоны указанным образом невозможно.
Пример 23.
В группе 30 человек. Может ли быть так, что 9 из них имеют по 3 друга, 11 – по 4, а 10 – по 5 друзей?
Решение. Если бы это было возможно, то можно было бы начертить граф с 30 вершинами, 9 из которых имели бы степень 3, 11 вершин – степень 4, 10 вершин – степень 5. У такого графа число нечетных вершин будет равно: 9 10 19. Это противоречит

24
утверждению, что число нечетных вершин любого графа четно. Поэтому поставленный в задаче вопрос имеет отрицательный ответ.
3.3. Маршруты, цепи, циклы
Маршрутом в графе называется чередующаяся последовательность вершин и ребер, в которой любые два соседних элемента инцидентны: V0 , l1 ,V2 , l2,...,lk, Vk . Вершины V0 и Vk называются концами цепи. Если начало и конец маршрута совпадают (V0 Vk ), то маршрут замкнут, в противном случае – открыт.
Цепью называется маршрут, в котором все ребра различны. Простой цепью называется маршрут, в котором все вершины (и
ребра) различны.
Цепь, соединяющая вершины V0 и Vk , обозначается (V0 , Vk). Циклом называется замкнутый маршрут, являющийся цепью. Простым циклом называется цикл, в котором все вершины,
кроме первой и последней, попарно различны.
Число циклов в графе G V, E обозначается Z G . Граф без циклов называется ациклическим.
Длиной маршрута называется количество ребер в нем (с повторениями). Если маршрут M = V0 , l1 ,V2 , l2,...,lk, Vk, то длина маршрута M равна k , обозначается М k .
3.4. Связность графа
Две вершины графа называются связными, если существует соединяющая их простая цепь. В противном случае две вершины называют несвязными.
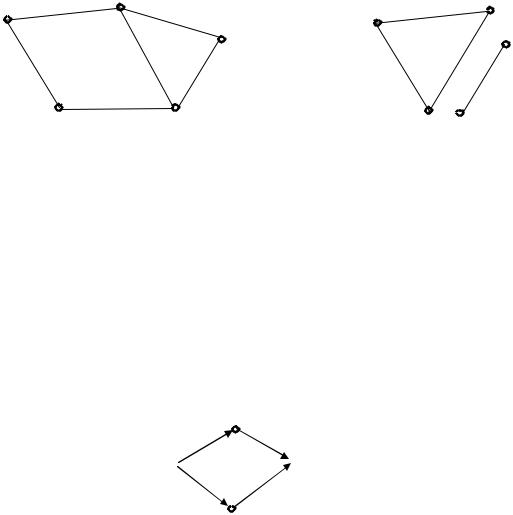
Граф называется связным, если каждые две вершины его связные. Граф называется несвязным, если хотя бы две его вершины несвязные. На рис. 4.1 изображены связный и несвязный графы.
|
|
25 |
|
|
V1 |
V2 |
V1 |
V2 |
|
V3 |
V3 |
|||
|
|
|||
V0 |
V4 |
V0 |
V4 |
Рис. 3.5. Связный и несвязный графы
3.5. Ориентированные графы
Ребро l графа G называется ориентированным, если одну вершину считают началом, а другую – концом, на рисунке его изображают стрелкой между вершинами. Граф называется ориентированным графом или орграфом, если все ребра у него ориентированы (рис. 5.1).
V1
V0 
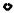 V2
V2
V3
Рис.3.6. Ориентированный граф
Одна и та же вершина ориентированного графа может служить началом для одних ребер и концом для других. По этой причине различают две степени вершины: степень выхода и степень входа.
Степенью выхода орграфа называется число выходящих из вершины ребер. Степенью входа вершины орграфа называется число входящих в вершину ребер. В орграфах в зависимости от сочетания степеней входа и выхода для данной вершины рассматриваются три случая.
Изолированной вершиной называется вершина, у которой и степень входа, и степень выхода равна 0. Источником называется вершина, степень выхода которой положительна, а степень
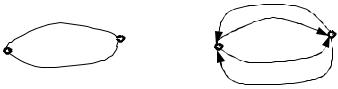
26
входа равна 0. Стоком называется вершина, степень входа которой положительна, а степень выхода равна 0. Петлей называется ребро, у которого начальная и конечная вершины совпадают. Петля обычно считается неориентированной.
Путем в ориентированном графе называется последовательность ориентированных ребер, то есть для орграфов цепь называется путем. Простым путем в орграфе называется путь, в котором ни одна вершина не содержится более одного раза. Ориентированным циклом или контуром в
ориентированном графе называется замкнутый путь. Длиной пути называется число ребер в этом пути.
Полным ориентированным графом называется граф, каждая пара вершин которого соединена в точности одним ориентированным ребром.
Если с каждого ребра полного ориентированного графа снять направление, то образуется полный граф с неориентированными ребрами (неориентированный полный граф).
Всякий полный ориентированный граф с n вершинами имеет простой ориентированный путь, проходящий через все вершины графа.
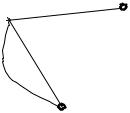
Мультиграфом называется граф, в котором пара вершин соединяется несколькими различными ребрами (рис. 3.7).
|
V2 |
|
V2 |
V1 |
V1 |
Рис. 3.7. Неориентированный и ориентированный мультиграф
3.6. Способы задания графов, матрицы смежности и инцидентности
Существуют три эквивалентных способа задания графов: аналитический, геометрический и матричный.
3.6.1. Графический способ.
Вершины изображают точками на плоскости, а ребра – линиями, соединяющими соответствующие точки (рис.3.8). Для
27
изображения ориентированного графа используется линия со стрелкой, указывающей направление от начала к концу дуги.
V1  е1 V2
е1 V2
е2
е3 V3
Рис.3.8. Способы задания графа
3.6.2. Аналитический способ.
Граф задают перечислением элементов множества вершин и множества ребер.
Для графа, изображенного на рис.3.8, эти множества включают:
V={V1, V2, V3} и Е={e1, e2, e3}, где e1=(V1, V2), e2=(V1, V3), e3=(V1, V3).
3.6.3. Матричный способ.
Ориентированный граф имеет вершины: V1 , V2 , …Vn и ребра: l1, l2, ….lm
а) Матрица смежности вершин – это квадратная матрица, в которой число строк и столбцов равно числу вершин n:
а11 |
а12 |
... |
а1n |
|
a22 |
... |
|
a21 |
a2n |
||
... |
... |
... |
... |
|
an2 |
... |
|
an1 |
ann |
Элементы этой матрицы определяются следующим образом. Элемент аij 1, если вершины Vi и Vj соединены между собой одним
ребром.
Элемент аij 0 , если вершины Vi и V j не соединены между собой. Элемент аii 1, если при вершине Vi имеется петля.
Элемент аij p , если вершины Vi и Vj соединены между собой р ребрами.
28
б) Матрица инцидентности – это прямоугольная матрица размером m n, число строк которой m равно числу вершин, а число столбцов n – числу ребер ориентированного графа.
Для неориентированного графа элементы этой матрицы определяются следующим образом:
1, если ребро l j инцидентно вершине Vi ;
аij 0, если ребро l j и вершина Vi не инцидентны
Для ориентированного графа элементы принимают значения:1, если ребро l j выходит из вершиныVi ;
аij 1, если ребро l j заходит в вершинуVi ;
0, если ребро l j и вершин Vi не инцидентны
ЗАДАНИЕ 5.
Граф G задан диаграммой. Для него:
1)составить матрицу смежности;
2)составить матрицу инцидентности;
3)указать степени вершин графа;
4)составить маршруты длины, равной 5;
5)составить цепь и простую цепь, соединяющие вершины V2 и V5;
6)построить простой цикл, содержащий вершину V4.
V1 |
2 |
V3 |
|
3 |
|||
|
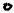 V4
V4
1 |
6 |
7 |
V2 |
|
4 |
|
V5 |
|
|
|
5 |
Решение.
1) Составим матрицу смежности вершин. Она является квадратной матрицей, в которой число строк и столбцов равно числу вершин n, в данном случае n 5 . Составим матрицу из пяти строк и пяти столбцов, запишем ее элементы в общем виде:
29
|
V1 |
V2 |
V3 |
V4 |
V5 |
|
|||||
V1 |
а11 |
а12 |
а13 |
а14 |
а15 |
||||||
V |
a |
21 |
a |
22 |
a |
23 |
a |
24 |
a |
25 |
|
2 |
|
|
|
|
|
|
|||||
V3 |
a31 |
a32 |
a33 |
a34 |
a35 |
||||||
V |
a |
41 |
a |
42 |
a |
43 |
a |
44 |
a |
|
|
4 |
|
|
|
|
|
45 |
|||||
V |
a |
a |
|
a |
a |
a |
|
|
|||
5 |
51 |
52 |
53 |
54 |
55 |
|
|||||
Заполняем первую строку:
a11 0 , так как при вершине V1 нет петли;
a12 1, так как вершины V1 и V2 соединены одним ребром; a13 1, так как вершины V1 и V3 соединены одним ребром; a14 0 , так как между вершинами V1 и V4 нет ребра;
a15 0 , так как между вершинами V1 и V5 нет ребра.
Аналогично заполняем 2-ю строку. Смотрим, с какими вершинами соединена вершина V2. Она соединена с вершинами V1, V3, V5 одним ребром. Поэтому элементы a21 , a23 , a25 равны 1, остальные равны 0.
Заполняем третью строку. Смотрим, с какими вершинами соединена вершина V3. Она соединена с вершинами V1, V2, V4 , V5 одним ребром. Поэтому элементы a31 , a32 , a34 , a35 равны 1, остальные равны 0.
Заполняем 4-ю строку. Вершина V4. соединена с вершинами V3 и V5 . Поэтому элементы a43 и a45 равны 1, остальные равны 0.
Заполняем 5-ю строку. Вершина V5. соединена с вершинами V2, V3 и V4. Поэтому элементы a52 , a53 , a54 равны 1, остальные равны 0.
Запишем матрицу смежности, в которую подставим полученные значения элементов:
V1 V2 V3 V4 V5
V1 |
0 |
1 |
1 |
0 |
0 |
V |
1 |
0 |
1 |
0 |
1 |
2 |
|
|
|
|
|
V3 |
1 |
1 |
0 |
1 |
1 |
V |
0 |
0 |
1 |
0 |
1 |
4 |
|
|
|
|
|
V |
0 |
1 |
1 |
1 |
0 |
5 |
|
|
|
|
|
