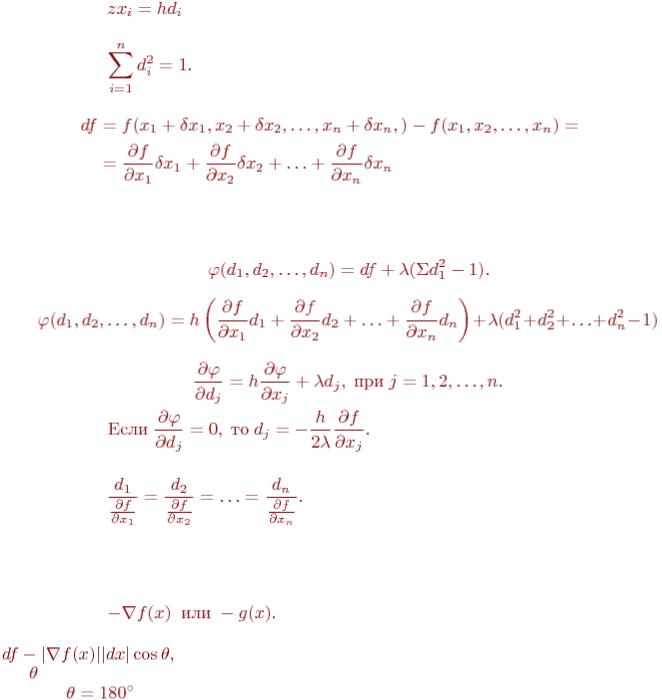
Введение в математическое программирование

6. Метод наискорейшего спуска

Суть данного метода заключается в том, что с помощью упомянутого ранее метода покоординатного спуска осуществляется поиск из заданной точки в направлении, параллельном одной из осей, до точки минимума в данном направлении. Затем поиск производится в направлении, параллельном другой оси, и т.д. Направления, конечно, фиксированы. Кажется разумным попытаться модифицировать этот метод таким образом, чтобы на каждом этапе поиск точки минимума производился вдоль "наилучшего" направления. Не ясно, какое направление является "наилучшим", но известно, что направление градиента является направлением наискорейшего возрастания функции. Следовательно, противоположное направление является направлением наискорейшего убывания функции. Это свойство может быть обосновано следующим образом.

Предположим, что осуществляется перемещение из точки x в следующую точку х + hd, где d - некоторое направление, a h - шаг некоторой длины. Следовательно, перемещение производится из точки (x1, х2, ..., хn) в точку (x1 + zx1, x2 + zх2, ..., хn + zхn), где

(6.1)

a dj - косинусы направления d, такие, что

(6.2)

Изменение значений функции определяется соотношениями

(6.3)

с точностью до первого порядка zxi, причем частные производные вычисляются в точке x. Как следует выбрать направления di, удовлетворяющие уравнению (6.2), чтобы получить наибольшее значение изменения функции df? Здесь возникает задача максимизации с ограничением. Применим метод множителей Лагранжа, с помощью которого определим функцию

Величина df, удовлетворяющая ограничению (6.2), достигает максимума, когда функция

достигает максимума. Ее производная

(6.5)

Следовательно,

(6.6)

Тогда di ~ df/dxi и направление d параллельно направлению V/(x) в точке х.

Таким образом, наибольшее локальное возрастание функции для заданного малого шага h имеет место, когда d есть направление Vf(x) или g(х). Поэтому направлением наискорейшего спуска является направление

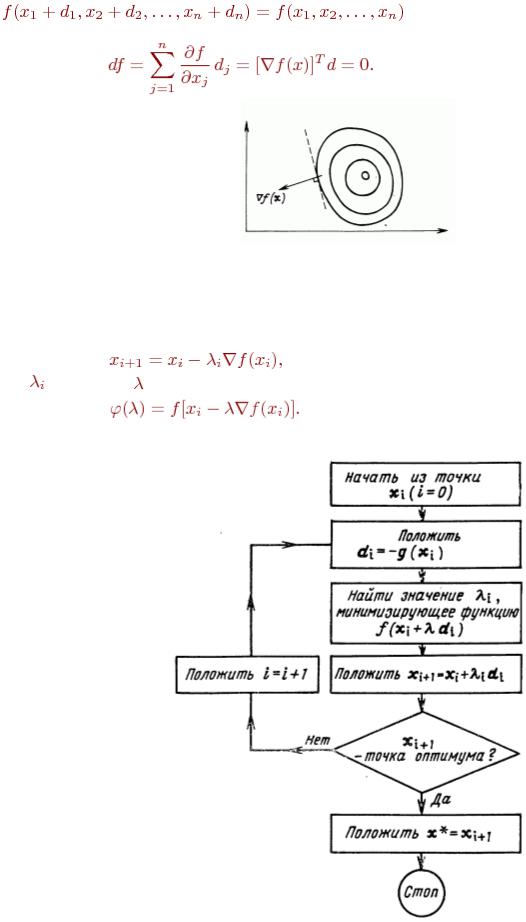
Замечание. Направление градиента перпендикулярно в любой точке линии постоянного уровня, поскольку вдоль этой линии функция постоянна. Таким образом, если (d1, d2, ..., dn) - малый шаг вдоль линии уровня, то

18

Введение в математическое программирование

и, следовательно,

(6.8)

Рис.13.

В методе наискорейшего спуска желательно использовать рассмотренное свойство направления градиента. Поэтому, если мы находимся в точке xi на некотором шаге процесса оптимизации, то поиск минимума функции осуществляется вдоль направления -Vf(xj). Данный метод является итерационным. На шаге i точка минимума аппроксимируется точкой xi. Следующей аппроксимацией является точка

Значение 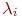может быть найдено с помощью одного из методов одномерного поиска. Блок-

схема метода наискорейшего спуска приведена на рис.14.

Рис.14.

19

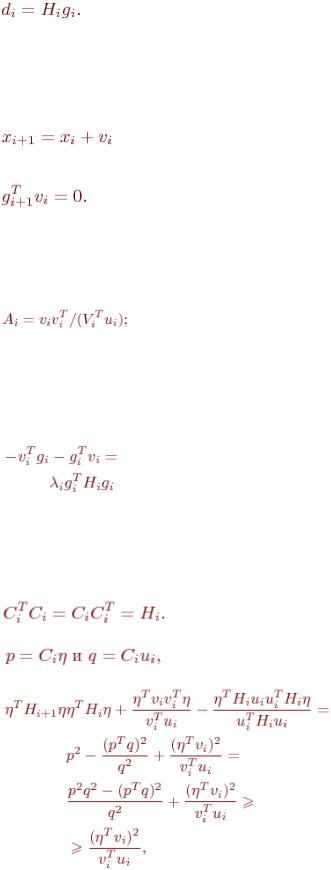
Введение в математическое программирование

7. Метод Давидона - Флетчера – Пауэлла

Начнем поиск из начальной точки x0, взяв в качестве начальной матрицу Н0 (обычно единичную матрицу, хотя в этом случае может подойти любая симметрическая положительно определенная матрица). Итерационная процедура может быть представлена следующим образом.

1.На шаге i имеются точка xi и положительно определенная симметрическая матрица Hi.

2.В качестве направления поиска взять направление

(7.1)

3.Чтобы найти функцию xi, минимизирующую функцию 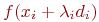, произвести одномерный поиск вдоль прямой .

4.Положить

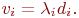(7.2) 5. Положить

(7.3)

6.Найти f(xi+1) и gi+6. Завершить процедуру, если величины |gi+1| или |Vi| достаточно малы. В противном случае продолжить.

7.Положить

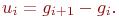(7.5) 8. Обновить матрицу H следующим образом:

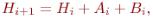(7.6) 9. где

(7.7)

10.

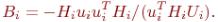
11.Увеличить i на единицу и вернуться на шаг 7.

Поясним процедуру, следуя аргументации Флетчера и Пауэлла.

а) Процесс будет устойчив, если функция vi убывает и величина 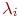положительна. Поскольку gi есть направление наискорейшего возрастания, функция vi будет убывать тогда, когда произведение

(7.9)

положительно.

Это справедливо, если Hi - симметрическая положительно определенная матрица для любого i. Начальная матрица Н0 обладает этими свойствами по определению. Процесс обновления в соответствии с соотношениями 7.6 – 7.8 сохраняет симметричность гессиана. Методом индукции докажем, что после обновления матрица Hi остается положительно определенной. Если это условие справедливо, то

(7.10)

Положим

(7.11)

где 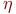- произвольный вектор. Тогда

(7.12)

20

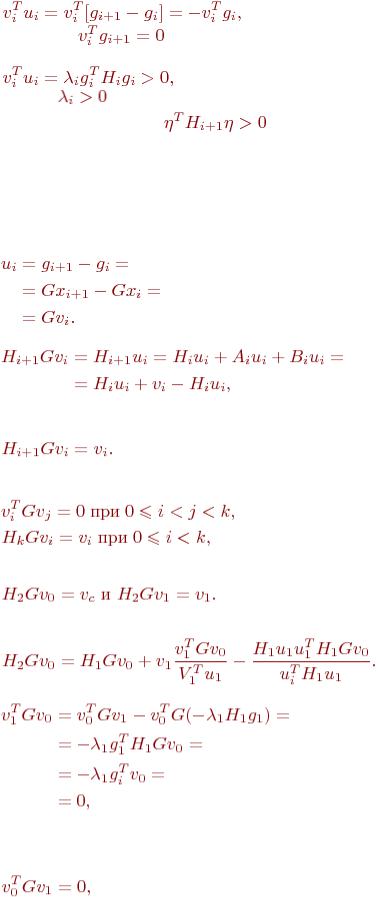
Введение в математическое программирование

поскольку 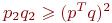согласно неравенству Шварца. Знаменатель в соотношении (7.12) положителен, так как

Нi+6.

б) Теперь покажем, что если метод ДФП применяется к квадратичной функции (с

линейно независимые собственные векторы матрицы Hk+1G с собственными значениями, равными единице. Тогда матрица HnG должна быть единичной.

Отметим, что из соотношения (7.5) следует, что

(7.14)

Кроме того,

что следует из соотношений (7.6) – (7.8) и из того, что 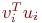и 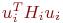можно сократить. Таким образом,

(7.15)

Далее методом индукции по k покажем, что для к = 2, 3, ..., n справедливы соотношения

(7.16)

(7.17)

Для доказательства в соотношении (7.15) положим i = 0 и получим H1Gv0 = v0, т.е. соотношение (7.17) при k = 6. При k = 2 соотношение (7.17) будет иметь вид

Второе равенство следует из соотношения (7.15) при i = 6. Для первого равенства имеем

Два последних члена в правой части равны нулю, поскольку

что следует из соотношения (7.15) при i = 0 и из соотношения (7.4) при i = 0. Кроме того, u1 =

Gv1, так что 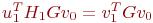. Таким образом, показано, что соотношение (7.17) справедливо при k = 7. После переноса в другую часть уравнения получим требуемый результат:

что является соотношением (7.6) при k = 7.

Теперь по индукции покажем, что если соотношения (7.16) и (7.17) справедливы при k, то они справедливы и при k + 6.

Имеем

21

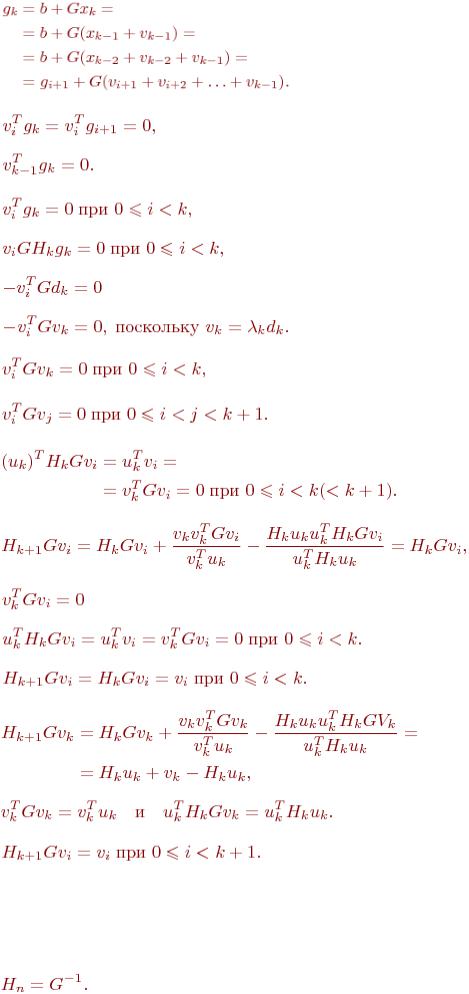
Введение в математическое программирование

(7.18)

Из соотношения (7.16) при I < k — 1 получим

и из соотношения (7.4) непосредственно следует, что

Тогда

(7.19)

и из соотношения (7.17) следует, что

причем

и

Следовательно,

(7.20)

т.е.

(7.21)

Из соотношений (7.14) и (7.17) также имеем

(7.22)

Тогда из соотношений (7.6) – (7.17) следует

так как

и

Таким образом, показано, что

(7.23)

При i = k имеем

поскольку

Следовательно, Hk+1Gvk = vk и из соотношения (7.23) получаем

(7.24)

Соотношения (7.21) и (7.24) так же справедливы для следующего k, как и соотношения (7.16) и (7.17). Следовательно, доказательство по индукции закончено. Из соотношения (7.16) следует, что векторы v0, v1, ..., vn-1 линейно независимы. Они являются взаимно сопряженными по отношению к матрице G. Из соотношения (7.17) следует, что v0, v1, ..., vn-1 являются собственными векторами матрицы HnG с собственным значением, равным единице. Тогда матрица HnG должна быть единичной. Следовательно,

(7.25)

22

Введение в математическое программирование

Из соотношения (7.19) следует, что минимум найден за n итераций. Вектор gn должен быть ортогонален каждому из n независимых векторов v0, v1, ..., vn-6. Следовательно,

(7.26)

в) Способ обновления матрицы H описывается в соотношении (7.6):

Покажем, что . Из условий ортогональности (7.16) следует

VTGV=D,

где V — матрица, состоящая из векторов vi, a D - диагональная матрица с элементами

.

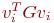Следовательно,

G=(VT)-1DV-1

Тогда

G-1=VDV-1VT,

а поскольку D - диагональная матрица, то можно произвести инверсию и перемножить матрицы для получения выражения

(см. соотношение (7.14)) Таким образом,

(7.27)

Поскольку соотношение (7.15) должно выполняться, то Нi+1Gvi - Vi, а это означает, что vi

= HiGvi + AiGvi + BiGvi. Так как

то

(7.28)

где z - произвольный вектор. Поскольку мы хотим, чтобы матрица Bi была симметрической, то выберем в качестве вектора z = Нiui, такой, чтобы

(7.29)

Этим завершается теоретическое изложение метода ДФП, который использует как идеи метода Ньютона — Рафсона, так и свойство сопряженных направлений, и при применении для минимизации квадратичной функции n переменных он сходится не более чем за n итераций. Это весьма мощная оптимизационная процедура, очень эффективная при оптимизации большинства функций независимо от того, квадратичны они или нет.

Ниже приведена блок – схема данной процедуры.

23