Практическая работа 7

Практическая работа № 7

Алгебра логики

Цель работы: Научиться определять истинность и ложность высказываний, применять логические операции, представлять логические выражения в виде выражений, выполнять упрощение выражений.

Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.

Например, «Сегодня идёт дождь» - это высказывание. В зависимости от погоды в каждый конкретный день это высказывание будет истинным или ложным.

Валгебре высказываний используются только утвердительные высказывания и при этом либо точно истинные, либо точно ложные.

Вбулевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные буквами латинского алфавита. Логические выражения (составные высказывания) называют логическими функциями, значение которых также только 0 и 1.

Таблица истинности – это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.

Различные варианты обозначения истинности или ложности представлены в таблице 1.

Таблица 1 - Варианты обозначения истинности и ложности высказываний

Основные логические операции

1.Инверсия (логическое отрицание) – одноместная логическая операция. Соответствует частице «НЕ», обозначается A или А .

Результат инверсии будет ложным, если исходное выражение истинно, и наоборот, результат будет истинным, если исходное выражение ложно.

Таблица истинности операции Инверсия представлена в таблице 2.

Таблица 2 - Таблица истинности операции Инверсия

2.Конъюнкция (логическое умножение) – двухместная операция логического умножения. Соответствует союзу «И», обозначается А В или А В, или А&В, или АВ.

Результат конъюнкции будет истинным тогда и только тогда, когда оба логических выражения истинны.

Таблица истинности операции Конъюнкция представлена в таблице 3.

1

Таблица 3 - Таблица истинности операции Конъюнкция

3.Дизъюнкция (логическое сложение) - двухместная операция логического сложения. Соответствует союзу «ИЛИ», обозначается А В , А+В.

Результат дизъюнкции будет ложным тогда и только тогда, когда оба логических выражения ложны.

Таблица истинности операции Дизъюнкция представлена в таблице 4.

Таблица 4 – Таблица истинности операции Дизъюнкция

4.Импликация (логическое следование) - условная двухместная логическая операция: Соответствует связке «Если…, то», обозначается А В .

Результат импликации будет ложным тогда и только тогда, когда условие истинно, а следствие ложно.

Таблица истинности операции Импликация представлена в таблице 5.

Таблица 5 - Таблица истинности операции Импликация

5.Эквивалентность (равнозначность) - двухместная логическая операция:

Соответствует связке «Тогда и только тогда, когда», обозначается А В , А В , A ~ B.

Результат эквивалентности будет истинным тогда и только тогда, когда значения исходных выражений совпадают.

Таблица истинности операции Эквивалентность представлена в таблице 6.

Результат неэквивалентности будет истинным тогда и только тогда, когда одно из исходных выражений истинно, а другое ложно.

2

Таблица истинности операции Исключающая дизъюнкция представлена в таблице 7.

Таблица 7 - Таблица истинности операции Сумма по модулю два

7. Штрих Шеффера (отрицание конъюнкций или дизъюнкция отрицаний) - двухместная логическая операция.

Результат штриха Шеффера будет ложным тогда и только тогда, когда оба исходных выражений истинно.

Таблица истинности операции Штрих Шеффера представлена в таблице 8.

Таблица 8 - Таблица истинности операции Штрих Шеффера

8. Стрелка Пирса (отрицание дизъюнкции или конъюнкция отрицаний) - двухместная логическая операция.

Результат стрелки Пирса будет истинным тогда и только тогда, когда оба исходных выражений ложны.

Таблица истинности операции Стрелка Пирса представлена в таблице 9.

Таблица 9 - Таблица истинности операции Стрелка Пирса

При вычислении значения логического выражения (формулы) логические операции вычисляются

вопределенном порядке, согласно их приоритету:

1)операции, заключённые в скобки;

2)инверсия;

3)конъюнкция;

4)дизъюнкция;

5)импликация и эквивалентность и т.д.

3

Столбцы группы Переменные содержат все варианты значений переменных, составляющих функцию. Для двух переменных таких сочетаний будет всего 4, а для трёх переменных их будет уже 8.

Построим таблицу истинности для p q r p q r

Элементарной конъюнкцией называется конъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причём среди переменных могут быть одинаковые.

Элементарной дизъюнкцией называется дизъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причём среди переменных могут быть одинаковые.

Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций. Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция элементарных конъюнкций. Совершенной ДНФ (СДНФ) называется ДНФ, в которой нет равных элементарных конъюнкций и все они содержат одни и те же переменные, причём каждую переменную только один раз (возможно с

отрицанием).

Совершенной КНФ (СКНФ) называется КНФ, в которой нет равных элементарных дизъюнкций и все они содержат одни и те же переменные, причём каждую переменную только один раз (возможно с отрицанием).

Таблица 10 - Таблица соответствия и несоответствия определению

4

Методика построения СДНФ по таблице истинности

В таблице истинности, по которой мы будем строить СДНФ, х и у – переменные, а F – результат вычислений логического выражения (значение функции).

1. Отмечаем те строки таблицы, в которых значение функции равно 1.

2.Выписываем для каждой из отмеченных строк комбинацию переменных через знак конъюнкции. Если переменная равна 1, то запишем её без отрицания, если же она равна 0, запишем эту переменную с отрицанием.

Таблица 11 - Таблица с элементарными конъюнкциями для функции F=0110

3. Все полученные выражения свяжем операцией дизъюнкцией и получим совершенную дизъюнктивную нормальную форму для данного логического выражения.

СДНФ= x y x y .

Методика построения СКНФ по таблице истинности

В таблице истинности, по которой мы будем строить СКНФ, х и у – переменные, а F – результат вычислений логического выражения (значение функции).

1. Отмечаем те строки таблицы, в которых значение функции равно 0.

5

2.Выписываем для каждой из отмеченных строк комбинацию переменных через знак дизъюнкции. Если переменная равна 0, то запишем её без отрицания, если же она равна 1, запишем эту переменную с отрицанием.

Таблица 12 - Таблица с элементарными дизъюнкциями для функции F=0110

3. Все полученные выражения свяжем операцией конъюнкцией и получим совершенную

конъюнктивную нормальную форму для данного логического выражения. СКНФ= x y x y .

Карты Карно-Вейча

Карта Карно — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения.

Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.

Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.

Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, таким образом вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.

Импликантой называется элементарное произведение, равное 1 на одном или нескольких наборах, где данная функция равна 1, и равное 0 на всех наборах, где данная функция равна 0. Импликанта покрывает один или несколько минтермов рассматриваемой булевой функции. Обычно, импликанта - это результат склеивания соответствующих минтермов или импликант.

Простая импликанта - это импликанта, которая содержит хотя бы минтерм функции, но перестает быть импликантой после удаления любого аргумента (иными словами, это импликанта, к которой не нельзя применить операцию склеивания).

Сокращенная ДНФ - это дизъюнкция всех простых импликант.

Существенная импликанта - это простая импликанта, образованная склеиванием таких минтермов, что по крайней мере для одного из них эта операция была единственной. Существенные импликанты образуют ядро функции.

Тупиковая ДНФ - это дизъюнкция простых импликант, из которых ни одна не является лишней. МДНФ (минимальная ДНФ) - тупиковая ДНФ с минимальным числом вхождений переменных

(минимальным числом букв) по сравнению с другими тупиковыми формами этой функции.

6

Имплицентой называется элементарная логическая сумма, равная 0 на одном или нескольких наборах, где данная функция равна 0, и равная 1 на всех наборах, где данная функция равна 1. Имплицента покрывает один или несколько макстермов рассматриваемой булевой функции. Обычно, имплицента - это результат склеивания соответствующих макстермов.

Простая имплицента - это имплицента, которая содержит хотя бы макстерм функции, но перестает быть имплицентой после удаления любого аргумента (иными словами, это имплицента, к которой не нельзя применить операцию склеивания).

Сокращенная КНФ - это конъюнкция всех простых имплицент.

Существенная имплицента - это простая имплицента, образованная склеиванием таких макстермов, что по крайней мере для одного из них эта операция была единственной. Существенные имплиценты образуют ядро функции.

Тупиковая КНФ - это конъюнкция простых имплицент, из которых ни одна не является лишней. МКНФ (минимальная КНФ) - тупиковая КНФ с минимальным числом вхождений переменных

(минимальным числом букв) по сравнению с другими тупиковыми формами этой функции.

Правила минимизации с использованием карт Карно

1.В карте Карно группы единиц (для получения ДНФ) и группы нулей (для получения КНФ) необходимо обвести четырехугольными контурами. Внутри контура должны находится только одноименные значения функции. Этот процесс соответствует операции склеивания или нахождения импликант данной функции.

2.Количество клеток внути контура должно быть целой степенью двойки (1, 2, 4, 8, 16...).

3.При проведении контуров крайние строки карты (верхние и нижние, левые и правые), а также угловые клетки, считаются соседними (для карт до 4-х переменных).

4.Каждый контур должен включать максимально возможное количество клеток. В этом случае он будет соответствовать простой импликанте.

5.Все единицы (нули) в карте (даже одиночные) должны быть охвачены контурами. Любая единица (нуль) может входить в контуры произвольное количество раз.

6.Множество контуров, покрывающих все 1 (0) функции образуют тупиковую ДНФ (КНФ). Целью минимизации является нахождение минимальной из множества тупиковых форм.

7.В элементарной конъюнкции (дизъюнкции), которая соответствует одному контуру, остаются только те переменные, значение которых не изменяется внутри обведенного контура. Переменные булевой функции входят в элементарную коньюнкцию (для значений функции 1) без инверсии, если их значение на соответствующих координатах равно 1 и с инверсией - если 0. Для значений булевой функции, равных 0, записываются элементарные дизьюнкции, куда переменные входят без инверсии, если их значение на соответствующих координатах равно 0 и с инверсией - если 1.

Например, необходимо построить МДНФ и МКНФ для функции f=10110101

Таблица 13 - Таблица истинности для функции F=10110101

7

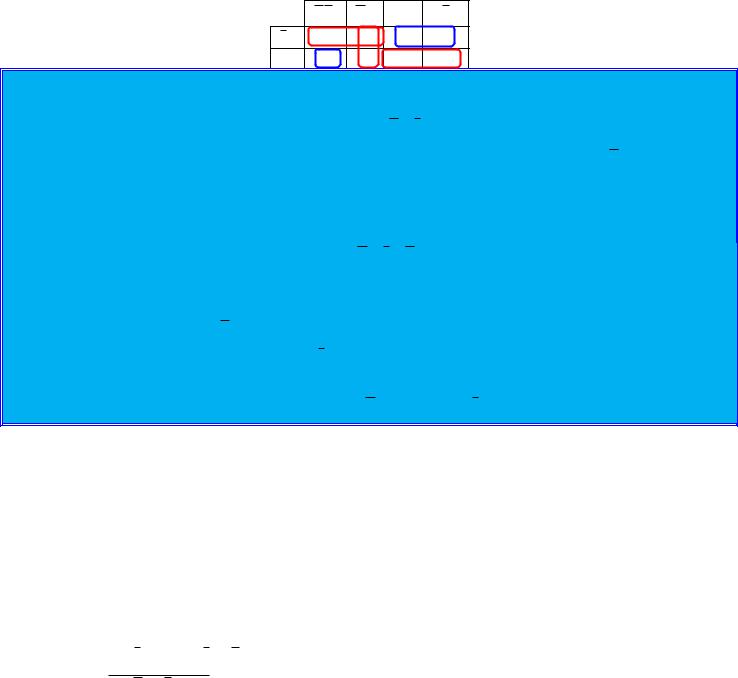
Таблица 14 - Карта Карно для функции F=10110101

Для построения МДНФ выделяем единицы (выделены красными прямоугольниками на таблице 14). Поскольку для первой группы переменная r неизменна, переменная q меняет значение с 0 на 1, а

переменная p неизменна, то импликанта имеет вид p r . Для второй группы переменная r меняет

значение с 0 на 1, а переменные q и p неизменны, следовательно импликанта имеет вид p q . Для третей группы переменная r неизменна, переменная q меняет значение с 0 на 1, а переменная p неизменна, следовательно импликанта имеет вид p r . Соединив полученные импликанты знаком дизъюнкции, получим минимальную дизъюнктивную нормальную форму:

МДНФ= p r p q p r

Для построения МКНФ выделяем нули (выделены синими прямоугольниками на таблице 14). Поскольку для первой группы переменные p и r неизменны, а переменная q меняет значение с 1 на 0, то

имплицента будет иметь вид p r . Вторая имплицента не состоит ни в одной из групп объединения,

поэтому она останется неизменной: p q r . Соединив полученные имплиценты знаком конъюнкции, получим минимальную конъюнктивную нормальную форму:

МКНФ= p r p q r

Задание №1 Определить истинность или ложность высказываний:

1.«2 2=5» и «2 2=4»

2.«2 2=5» или «2 2=4»

3.«2 2=5» и «2 2=4» или «2 2=3»

4.«2 2=5» или «2 2=4» или «2 2=3»

5.«2 2=5» или «2 2=4» и не «2 2=3»

6.«2 2=4» и не «2 2=3» и не «2 2=5»

Задание №2 Построить таблицу истинности:

1.q r p r q ;

2.r p r p .

Таблица 15 - Варианты значения функции

8

Таблица 16 - Продолжение таблицы 15

Задание №3 Построить совершенную дизъюнктивную нормальную форму (СДНФ) и совершенную конъюнктивную нормальную форму (СКНФ) для функции своего варианта (варианты представлены в таблице 15), который определяется по номеру в журнале.

Задание №4 Построить минимальную дизъюнктивную (МДНФ) и минимальную конъюнктивную (МКНФ) формы функции с использованием метода Карно-Вейча для функции своего варианта (варианты представлены в таблице 15), который определяется по номеру в журнале.

Задание №5 Оформить отчет по лабораторной работе (форма отчета приведена в Приложении) и отправить его на проверку преподавателю электронной почтой: SorokinaSV.4@gmail.com

9

ПРИЛОЖЕНИЕ

Титульный лист должен иметь вид:

Нижний колонтитул всех листов кроме титульного должен содержать рамку со штампом (высота надписи штампа – 1,5 см; ширина надписи – 18,5 см; 1 столбец таблицы – 0,7 см; 2 столбец

– 1 см; 3 столбец – 2,3 см; 4 столбец – 1,5 см; 5 столбец – 1 см; 6 столбец – 11 см; 7 столбец – 1 см):

10