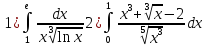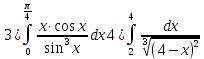Практическое занятие по теме «Определённый интеграл»
.docxПрактическое занятие по теме «Определённый интеграл»
Теоретические аспекты
Пусть функция y = f(x) определена на отрезке [a;b]
c1 ci cn
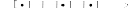 X
X
a=x0 x1 … xi-1 xi … xn = b
ci
ϵ
[xi-1
; xi]
 xi
= xi
– xi-1
xi
= xi
– xi-1
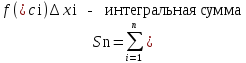
Если интегральная сумма Sn имеет предел, который не зависит ни от способа разбиения отрезка [a;b] на малые отрезки, ни от выбора точек в каждом из них,
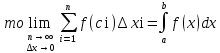
Теорема
1 (Коши)
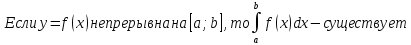
Теорема 2 (формула Ньютона-Лейбница)
Если f (x) - непрерывна на [a;b] и F(x) — её любая первообразная на этом отрезке, то имеет место равенство:
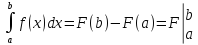
Основные свойства:
Если
y
= f(x)
интегрируема на [a;b],
то
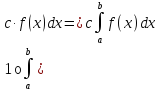
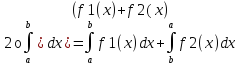

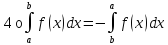
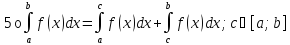
6о. (теорема о среднем)
Если
f(x)
непрерывна на [a;b], то существует такая
точка
c ϵ [a;b],что
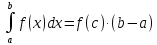
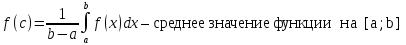
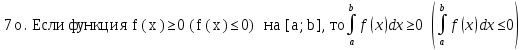
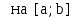
8о.
Если
f1(x),
f2(x)-
непрерывны
на [a;b]
и f1(x)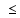 f2(x)
на [a;b],
f2(x)
на [a;b],

9о. (оценка интеграла)
Если
m
– наименьшее, M
– наибольшее значения функции f(x)
на
[a;b],
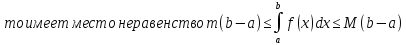
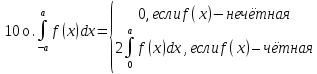
11о. Производная определённого интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом
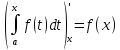
Геометрический смысл определённого интеграла
Если f(x)
непрерывна и положительна на [a, b],
то интеграл
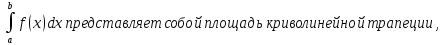
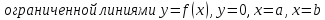

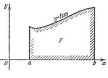
Физический смысл определённого интеграла
Пусть некоторая материальная точка M перемещается под действием силы F= F(x), которая направлена вдоль оси абсцисс (здесь x – абсцисса движущейся точки M).
Работа переменной силы F, величина которой есть непрерывная функция F= F(x), действующей на отрезке [a;b], равна определенному интегралу от величины F(x) силы, взятому по

Методы интегрирования
-
Замена переменной
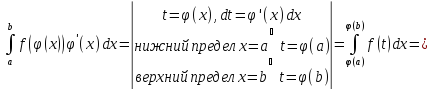
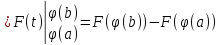
-
Интегрирование по частям
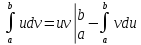
где u=u(x) , v=v(x) – непрерывны на [a, b]; du=u’(x)dx , dv=v’(x)dx
Несобственные интегралы
I рода (промежуток интегрирования бесконечен) :

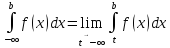
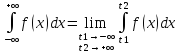
II рода (на [a;b] существует точка c в которой f(c) имеет разрыв):
1. если точка разрыва - a (или b)
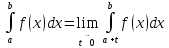
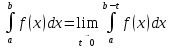
2. если c ϵ [a;b] - точка разрыва
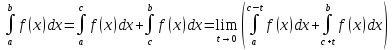
Замечание: При этом несобственный интеграл называется сходящимся если предел конечен, и расходящемся если предел равен ∞ или не существует
Практические задания
№1 Вычислить определённый интеграл

№2 Вычислить определённый интеграл

№3 Вычислить определённый интеграл
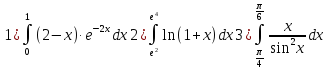
№4 Вычислить несобственный интеграл (бесконечный интервал интегрирования)
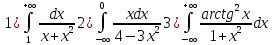
№5 Вычислить несобственный интеграл (разрыв функции на интервале интегрирования)