
Матанализ 4 Вариант
.doc
Контрольная работа №1.
Вариант по последней цифре шифра
Задание 1. Вычислить указанные пределы, не пользуясь правилом Лопиталя а), б), в), г), д).
а)
4.
б)
4.
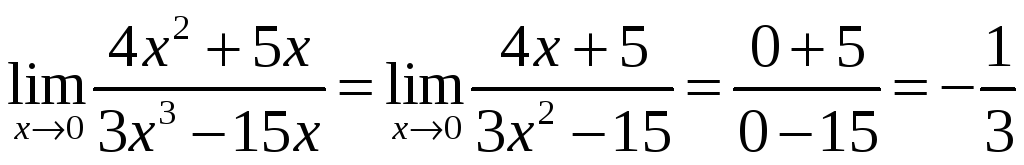 ,
,
в)
4.
 ,
,
г) 4.
![]() ,
,
д)
4.
 ,
,
Задание 2. Вычислить производные функций а), б), в), г):
а) 4.![]() ,
,

б) 4.![]() ,
,
![]()
в) 4.![]() ,
Логарифмируем это:
,
Логарифмируем это:
![]()
Теперь дифференцируем:

Следовательно,
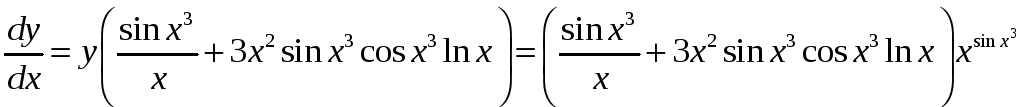
г) 4.![]() ,
продифференцируем это
,
продифференцируем это
![]() ,
откуда
,
откуда
![]() ,
и тогда
,
и тогда

Задание 3.Вычислить производные второго порядка функций:
4.
 ―
найдём сперва первые производные:
―
найдём сперва первые производные:
![]() ,
,
 , теперь вторую производную
, теперь вторую производную

Тогда

Задание 4. Провести исследование функций и построить их графики а), б).
а) 4. ,
,
Решение. Видно, что функция определена на всём множестве действительных чисел, за исключением выколотой точки х=0, где знаменатель обращается в нуль. Следовательно, х=0 ― точка разрыва второго рода, х=0 ― вертикальная асимптота графика.
Найдём производную этой функции:
![]() .
Приравняв её нулю, видим, что в нуль
эта производная обращается только при
x=-2. Следовательно, точка (-2, 3) ―
подозрительная на экстремум
.
Приравняв её нулю, видим, что в нуль
эта производная обращается только при
x=-2. Следовательно, точка (-2, 3) ―
подозрительная на экстремум
Найдём вторую
производную:
 .
В точке х=-2 её значение равно 3/2.
Следовательно, точка (-2, 3) ― это точка
минимума. Нулю вторая производная не
бывает равна, следовательно, точек
перегиба нет. Вторая производная всегда
положительна, следовательно, функция
вогнутая на всей области определения.
.
В точке х=-2 её значение равно 3/2.
Следовательно, точка (-2, 3) ― это точка
минимума. Нулю вторая производная не
бывает равна, следовательно, точек
перегиба нет. Вторая производная всегда
положительна, следовательно, функция
вогнутая на всей области определения.
Отсюда можно без труда заключить, что на промежутке (-∞, -2) функция убывает, на промежутке (-2, 0) ― возрастает, и на промежутке (0, +∞) ― убывает.
Кроме того, эти два примера с дифференцированием позволяют предположить, что функция непрерывная и гладкая на всей области определения.
Попробуем функцию на чётность:
 ,
видно, что
,
видно, что
![]() ― функция не обладает чётностью или
нечётностью, график не имеет элементов
симметрии. Нулевое значение функция
может приобрести при
― функция не обладает чётностью или
нечётностью, график не имеет элементов
симметрии. Нулевое значение функция
может приобрести при
![]() .
.
Устремим х®-∞
 ,
т.е., у функции нет горизонтальных
асимптот.
,
т.е., у функции нет горизонтальных
асимптот.
 ,
следовательно, есть наклонная асимптота
вида y=-x+b.
,
следовательно, есть наклонная асимптота
вида y=-x+b.
 ,
следовательно, наклонная асимптота
есть y=-x.
,
следовательно, наклонная асимптота
есть y=-x.
Построим график нашей функции на небольшом участке, содержащем все особые точки, найденные нами.

б) 4.![]()
Решение. Видно, что функция определена на всём множестве действительных чисел. Следовательно, точек разрыва нет, вертикальных асимптот графика нет.
Найдём производную этой функции:
![]()
Приравняв её нулю, видим, что в нуль эта производная обращается только при x=3. Следовательно, точка (3, 1) ― подозрительная на экстремум
Найдём вторую производную:
 .
В точке х=3 её значение равно -1.
Следовательно, точка (3, 1) ― это точка
максимума. Нулю вторая производная
становится равна при х=4, следовательно,
(4, 2/е) ― точка перегиба.
.
В точке х=3 её значение равно -1.
Следовательно, точка (3, 1) ― это точка
максимума. Нулю вторая производная
становится равна при х=4, следовательно,
(4, 2/е) ― точка перегиба.
Отсюда можно без труда заключить, что на промежутке (-∞, 3) функция выпуклая, возрастает, на промежутке (3, +∞) ― убывает, выпукло-вогнутая (перегиб в точке х=4).
Кроме того, эти два примера с дифференцированием позволяют предположить, что функция непрерывная и гладкая на всей области определения.
Попробуем функцию на чётность:
![]() ,
видно, что
,
видно, что
![]() ― эта функция не является чётной либо
нечётной, график лишён элементов
симметрии. Нулевое значение функция
может приобрести в бесконечном пределе.
― эта функция не является чётной либо
нечётной, график лишён элементов
симметрии. Нулевое значение функция
может приобрести в бесконечном пределе.
Устремим х®-∞
![]() ,
т.е., у функции есть горизонтальная
асимптота у=0.
,
т.е., у функции есть горизонтальная
асимптота у=0.
 ,
следовательно, наклонных асимптот нет
,
следовательно, наклонных асимптот нет
Построим график нашей функции на небольшом участке, содержащем все особые точки, найденные нами.

Задание 5. Исследовать на экстремум следующие функции двух переменных:
4.
![]() .
.
Решение. Найдем частные производные функции:
![]() ,
,

Чтобы исследовать функцию на экстремум, приравняем частные производные нулю:
 ,
откуда
,
откуда

Найдем вторые производные:
 ,
,
 ,
,

Построим гессиан
функции:

Определитель его
есть

Так как гессиан отрицательно определен, то в точке (0, -2) нет экстремума, следовательно, это седловая точка.

Задание 6. Найти наибольшее и наименьшее значения функций в указанных областях.
![]() в треугольнике
в треугольнике
![]() ,
,
![]() ,
,
![]() .
.
Решение. Вычертим эту область

Найдём значение функции на граничных точках: z(4, -4)=16, z(4, 4)=0, z(-4, 4)=16
Найдём возможный экстремум функции внутри этой области:
![]() ,
,
 ,
приравняв эти производные нулю, получим
х=2, у=2, z(2, 2)=4.
,
приравняв эти производные нулю, получим
х=2, у=2, z(2, 2)=4.
Положим х=4, тогда
наша функция есть
![]() .
Следовательно,
.
Следовательно,
 ,
экстремума быть не может.
,
экстремума быть не может.
Положим у=4, тогда
наша функция есть
![]() ,
испытаем это на экстремум:
,
испытаем это на экстремум:
![]() ,
экстремума быть не может.
,
экстремума быть не может.
Положим y=-х, тогда
наша функция есть
![]() ,
испытаем это на экстремум:
,
испытаем это на экстремум:
![]() ,
приравняв нулю, получим точку (0, 0), z(0,
0)=0.
,
приравняв нулю, получим точку (0, 0), z(0,
0)=0.
Таким образом,
видим, что
![]() ,
,
![]()

Задание 7. Найти интегралы а), б), в), г), д).
а) 4.
![]() .
.
Положим такую
замену:
 , тогда можно перейти к такому интегралу
, тогда можно перейти к такому интегралу

Переходим к старой переменной, получаем

б)
4.
![]() .
― возьмём этот интеграл по частям
.
― возьмём этот интеграл по частям
Обозначим

Тогда, в соответствии с формулой, получим

Второй интеграл опять берём по частям

Получаем:

В)
4.
 .
.
Сравнивая с видом исходной дроби, видим
 , откуда, конечно
, откуда, конечно
![]()
Тогда имеем

г) 4.
![]() ― введём такую замену
― введём такую замену
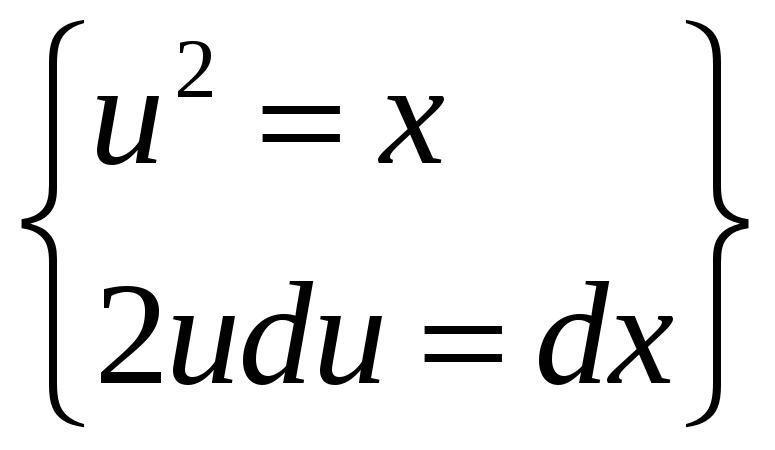 ,
получаем интеграл
,
получаем интеграл
 ,
возвращаясь к старой переменной, получим
,
возвращаясь к старой переменной, получим

д)
4.
 .
.
Задание 8. Вычислить площади фигур, ограниченных линиями, заданными уравнениями.
4.

Решение. Вычертим такую фигуру

Решение. Площадь фигуры можно представить в виде
![]() ,
где
,
где
![]()
Определим пределы
интегрирования:
![]() ,
откуда
,
откуда
 ,
следовательно,
,
следовательно,
![]()
Таким образом,

Задание 9. Вычислить длины дуг кривых, заданных уравнениями в полярных координатах.
4.
![]()
Решение. Построим данную кривую

В данном случае длина дуги выражается интегралом

Контрольная работа №2.
Задание 1. Установить характер сходимости ряда с общим членом un.
4.

Решение. Так как
это знакопеременный ряд, то применим
признак Лейбница:
 .
Так как члены ряда монотонно убывают
по величине и стремятся к нулю, данный
ряд сходится.
.
Так как члены ряда монотонно убывают
по величине и стремятся к нулю, данный
ряд сходится.
Проверим его на
условную сходимость. Используем
радикальный признак Коши

Так как
![]() ,
то данный ряд, бесспорно, сходится.
,
то данный ряд, бесспорно, сходится.
Следовательно,
ряд
 ― сходящийся.
― сходящийся.
Задание 2. Найти область сходимости степенного ряда с общим членом un.
4.

Решение. Найдём радиус сходимости ряда по формуле

Далее найдём область абсолютной сходимости ряда:
 ,
,
 ,
следовательно, область сходимости
степенного ряда есть
,
следовательно, область сходимости
степенного ряда есть
![]()
Исследуем ряд на
концах интервалов сходимости. Пусть
![]() ,
тогда наш ряд
,
тогда наш ряд
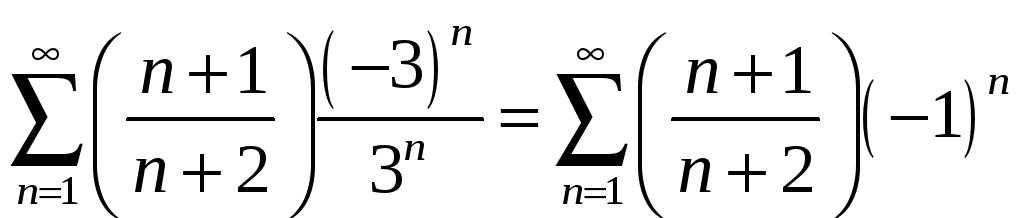 .
Это знакопеременный ряд. Применим
признак Лейбница:
.
Это знакопеременный ряд. Применим
признак Лейбница:
 .
Так как члены ряда не стремятся к нулю,
то ряд является расходящимся, следовательно,
точка
.
Так как члены ряда не стремятся к нулю,
то ряд является расходящимся, следовательно,
точка
![]() не входит в область абсолютной сходимости.
не входит в область абсолютной сходимости.
Далее, пусть
![]() ,
тогда имеем ряд
,
тогда имеем ряд
 ― это расходящийся ряд, как это уже было
показано. Следовательно, точка
― это расходящийся ряд, как это уже было
показано. Следовательно, точка
![]() не входит в область абсолютной сходимости
ряда.
не входит в область абсолютной сходимости
ряда.
Ответ: в области
![]() ряд сходится абсолютно.
ряд сходится абсолютно.
Задание 3. Найти решение задачи Коши.
4.
![]()
Обозначим
![]() , тогда
, тогда

И теперь получаем

И тогда
![]() ,
проинтегрируем
,
проинтегрируем
![]() или
или
![]() ,
теперь можно найти частное решение,
используя условие y'(0)=1. Имеем x=0, cosx=1,
тогда
,
теперь можно найти частное решение,
используя условие y'(0)=1. Имеем x=0, cosx=1,
тогда
![]() ,
откуда, конечно, С1=0, и частное
решение, интересующее нас, есть u=cos2y.
,
откуда, конечно, С1=0, и частное
решение, интересующее нас, есть u=cos2y.
Возвращаемся к старой переменной:
![]() или
или
 ,
откуда tgy=x+C2
или в явном виде
,
откуда tgy=x+C2
или в явном виде
![]()
Найдём теперь частное решение, подставим y(0)=0, получим
![]() ,
откуда конечно, С2=0, тогда имеем
окончательный ответ y=arctgx
,
откуда конечно, С2=0, тогда имеем
окончательный ответ y=arctgx
Задание 4. Найти общее решение дифференциального уравнения.
4.
![]()
Решение. Сначала
необходимо найти общее решение
неоднородного уравнения
![]()
Запишем
характеристическое уравнение m2+m+1=0.
У него комплексные корни
 ,
поэтому общее решение надо искать в
виде
,
поэтому общее решение надо искать в
виде

Теперь необходимо найти частное решение этого уравнения в виде
![]() ,
судя по виду правой части
,
судя по виду правой части
Найдем соответствующие производные:
![]()
![]()
Конструируем исходное уравнение:
![]()
Теперь, сравнивая с видом исходной правой части, убеждаемся
 или
или

Отсюда
![]()
Таким образом, искомое общее решение неоднородного уравнения

Задание 5. Операционным методом решить задачу Коши.
![]() ,
поскольку не заданы начальные условия,
то решения нет.
,
поскольку не заданы начальные условия,
то решения нет.
Задание 6. Функцию
![]() разложить в указанном интервале в ряд
Фурье и в ряд Фурье по синусам:
разложить в указанном интервале в ряд
Фурье и в ряд Фурье по синусам:
4.

Решение. Вычислим Фурье-коэффициенты при синусах.

Таким образом, наше Фурье-представление:

Задание 7. Изменить порядок интегрирования в следующих интегралах:
![]()
Решение. Вычертим область интегрирования, чтобы было легче ориентироваться

Обе кривые пересекаются в точках (-1, 1) и (1, 1). Искомая фигура находится книзу от точки пересечения этих кривых.
Таким образом,

Задание 8. Найти объем тела, заданного ограничивающими его поверхностями.
![]()
Решение. Проекция такой фигуры на плоскость XOY выглядит как

Объём можно вычислить соответствующим тройным интегралом

Задание 9. Вычислить криволинейные интегралы по координатам
![]() ,
где l-окружность
,
где l-окружность
![]() при положительном направлении обхода.
при положительном направлении обхода.
Вычислим
![]()
Тогда получаем

Задание10. Вычислить криволинейные интегралы по длине дуги.
![]() ,
где l–отрезок АВ; А(-1;0), В(0;1).
,
где l–отрезок АВ; А(-1;0), В(0;1).
Решение. Ищем
дифференциал длины дуги
![]()
Уравнение отрезка
АВ есть у=х+1, тогда dx=dy,
и
![]()

Задание 11. Даны
векторное поле
![]() и плоскость
и плоскость
![]() ,
которая совместно с координатными
плоскостями образует пирамиду. Найти:
,
которая совместно с координатными
плоскостями образует пирамиду. Найти:
1) поток векторного поля через полную поверхность пирамиды в направлении внешней нормали непосредственно и по теореме Остроградского-Гаусса;
2) циркуляцию векторного поля вдоль замкнутого контура, ограничивающего часть плоскости (р), вырезаемую координатными плоскостями, применив теорему Стокса.
![]() .
.
Решение. Приводим
уравнение плоскости
![]() к виду
к виду
![]() ,
где
,
где
![]() – отрезки, отсекаемые плоскостью на
осях координат.
– отрезки, отсекаемые плоскостью на
осях координат.
Поделим обе части
уравнения на 2, получим
![]() .
.
Построим эту
плоскость. По оси
![]() она отсекает 1; по оси
она отсекает 1; по оси
![]() она отсекает отрезок -2; по оси
она отсекает отрезок -2; по оси
![]() она отсекает 1.
она отсекает 1.
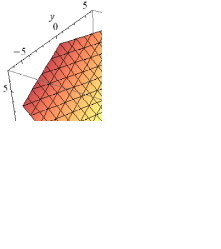
Циркуляцию
векторного поля
![]() находят по формуле:
находят по формуле:
![]() .
.
Учитывая, что
![]() ,
,
![]() ,
получаем
,
получаем
![]() ,
где
,
где
![]() – контур треугольником
– контур треугольником
![]() состоит из трех отрезков:
состоит из трех отрезков:
![]() ,
,
![]() и
и
![]() ,
поэтому интеграл разбиваем на три
интеграла:
,
поэтому интеграл разбиваем на три
интеграла:
1) по отрезку
![]() ;
2) по отрезку
;
2) по отрезку
![]() ;
3) по отрезку
;
3) по отрезку
![]() .
.
1). Уравнение прямой
![]() (
(![]() –
линия пересечения плоскости
–
линия пересечения плоскости
![]() с координатной плоскостью
с координатной плоскостью
![]() ),
имеет вид:
),
имеет вид:
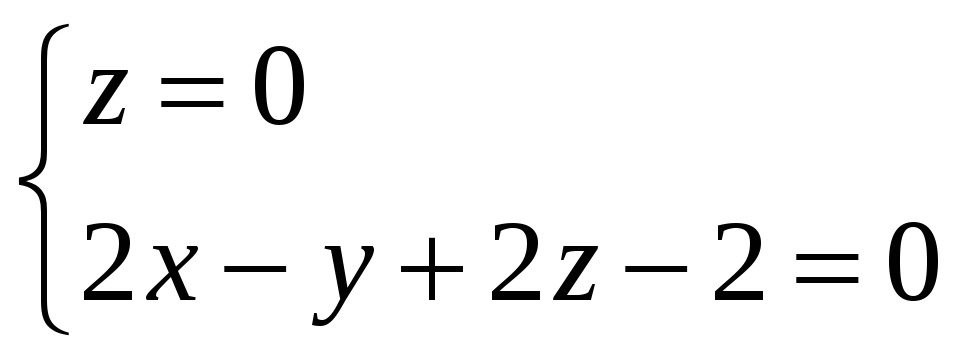
![]()


2). Уравнение прямой
![]() имеет
вид:
имеет
вид:

![]()

![]()
3). Уравнение прямой
![]() имеет вид:
имеет вид:

![]()


Вычисляем циркуляцию:
![]()
Вычисляем циркуляцию по формуле Стокса:
 ;
;
В формуле здесь
![]() ,
,
![]() ,
,
![]() – координаты векторного поля
– координаты векторного поля
![]() ,
,
![]() – плоский треугольник
– плоский треугольник
![]() .
Имеем
.
Имеем
![]() ,
,
![]() ,
тогда
,
тогда
 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
 .
В формуле Стокса
.
В формуле Стокса
![]() ,
,
![]() ,
,
![]() – координаты единичного вектора нормали
к поверхности. В данном случае
– координаты единичного вектора нормали
к поверхности. В данном случае
![]() и
и
![]() берем со знаком «–», т.к. нормаль образует
тупой угол с осью
берем со знаком «–», т.к. нормаль образует
тупой угол с осью
![]() и с осью
и с осью
![]() .
.
Отсюда получаем по формуле Стокса

Вычислим поток
векторного поля
![]() по внешней стороне треугольника
по внешней стороне треугольника
![]() .
Из уравнения плоскости
.
Из уравнения плоскости
![]() находим:
находим:
![]() ;
;
![]() ;
;
 .
.
Запишем уравнение
плоскости
![]() в виде:
в виде:
![]() ;
координаты нормального вектора плоскости
;
координаты нормального вектора плоскости
![]() ,
,
![]() ,
тогда единичный вектор нормали равен
,
тогда единичный вектор нормали равен
 .
.
Поток находим по формуле:
![]() ,
где
,
где
 .
.
В нашем примере
 ,
найдем скалярное произведение
,
найдем скалярное произведение
![]() и
и
![]() .
Имеем:
.
Имеем:
![]()
итак,
 .
.
Здесь треугольник
![]() это проекция треугольника
это проекция треугольника
![]() на плоскость
на плоскость
![]() .
Вместо
.
Вместо
![]() подставим
подставим
![]() .
.
