
romanovskiy_romanovskaya_elementy_teorii_veroyatnostey
.pdf
= |
пл.d1 |
+ |
пл.d2 |
– |
пл.d3 |
= Р(А) + Р (В) – Р (АВ), |
пл.D |
пл.D |
пл.D |
что и требовалось доказать.
Замечание 1. События А, В называются несовместными, если они не могут произойти одновременно при данном испытании. Для несовместных событий справедлива формула
Р (А + В) = Р (А) + Р (В). |
(6) |
Вероятность суммы несовместных событий равна сумме вероятностей этих событий.
В самом деле, по теореме сложения имеем:
P( A + B) = P( A) + P(B) - P( A × B) = P( A) + P(B) - 0 .
{
O
Замечание 2. Справедлива формула:
Р(А) = 1 – Р ( A ).
Вероятность наступления события равна единице минус вероятность ненаступления события. В самом деле:
A + A = W ;
A × A = O .
Откуда имеем:
P( A + A) = P(W) = 1 ,
P( A + A) = P( A) + P( A) ,
следовательно,
Р(А) + Р ( A ) = 1, то есть Р(А) = 1 – Р ( A ).
Условная вероятность. Теорема умножения вероятностей
Пусть с испытанием связаны события А,В. Запись Р(В/А) означает: вероятность события В при условии, что событие А наступило.
Поясним на примере.
21
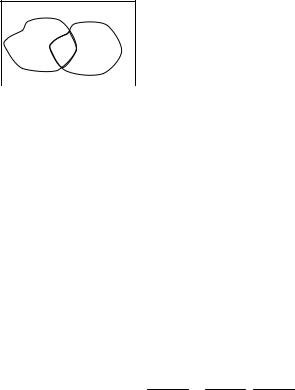
Испытание: берут наугад точку в области D равновозможным образом.
d1 d3 d2 Событие А: попадание в область d1; Событие В: попадание в область d2.
|
|
|
|
D |
|
|
|
|
Рис. 5 |
|
Тогда, имеем (рис.5): |
|
|
||
|
пл.d |
2 |
|
|
благоприятная площадь |
пл. d3 |
|
Р(В)= |
|
, |
Р(В/А) = вся возможная площадь = |
|
|
||
|
пл. d1 . |
||||||
|
|
||||||
|
пл.D |
|
|
|
|
||
Вероятность Р(В/А) называется условной вероятностью.
Теорема 2. Справедлива формула
P( A × B) = P( A) × P(B / A) . |
(7) |
Вероятность произведения двух событий равна вероятности одного из них, умноженного на вероятность другого при условии, что первое наступило.
Доказательство. Доказательство проведем в рамках схемы геометрической вероятности (рис. 5).
P( A × B) = пл. d 3 = пл. d1 × пл. d 3 = P( A) × P(B / A) .
пл. D пл. D пл. d1
Замечание. 1. Будем говорить, что событие В не зависит от события А, если выполняется равенство Р(В/А) = Р(В), в этом случае
P( A × B) = P( A) × P(B) . |
(8) |
Вероятность произведения независимых событий равна произведению вероятностей этих событий.
Доказать самостоятельно:
если событие В не зависит от события А, то событие А не зависит от В.
22

2. P( A × B × C ×K) = P( A) × P(B / A) × P(C / AB) ×K.
Пример. В урне содержится 7 белых и 3 черных шара
7 б |
(рис. 6). |
3 ч |
Испытание: из урны берут наугад два |
Рис. 6 |
шара равновозможным образом. |
Найти вероятность того, что они: |
а) оба белые (Р(бб) – ?); б) оба черные (Р (чч) – ?); в) одного цвета; г) разного цвета.
Решение.
I способ. По определению вероятности (1) (гл.1§1) и по формуле (2) имеем:
а) Р(бб) = |
|
m |
= |
|
C72 |
= |
7 |
; |
||||
|
|
C102 |
|
|
||||||||
|
|
n |
|
|
15 |
|
|
|||||
б) Р(чч) = |
m |
= |
C32 |
|
= |
1 |
. |
|||||
|
C102 |
|
|
|||||||||
|
|
n |
|
|
|
15 |
|
|||||
II способ. По формулам (6) и (7) имеем:
а) Р(бб) = Р (1й белый и 2й белый) = Р(1й белый) ·Р (2й б/ 1й б) =
= 7 × 6 = 7 . 10 9 15
б) Р(чч) = Р (1й черный и 2й черный) = Р(1й ч) ·Р (2й ч/ 1й ч) =
= 3 × 2 = 1 . 10 9 15
в) Р(одного цвета) =Р (1й б и 2й б или 1й ч и 2й ч) = Р(бб + чч) =
= Р(бб) + Р (чч) = 7 + 1 = 8 . 15 15 15
г) I способ.
Р (разного цвета) = Р (б·ч + ч·б) = Р (б·ч) + Р(ч·б) =
7 × 3 + 3 × 7 = 42 = 7 . 10 9 10 9 90 15
23
II способ. |
|
|
|
|
|
Р (разного цвета) = 1 – Р (одного цвета) = 1 – |
|
8 |
= |
7 |
. |
15 |
|
||||
|
15 |
|
|||
§ 5. Формула полной вероятности. Формула Байеса
Рассмотрим следующую задачу. Имеются три урны с указанным количеством белых и черных шаров (рис. 7).
I |
II |
III |
7 б |
4 б |
2 б |
3 ч |
6 ч |
8 ч |
Рис. 7
Испытание: из наугад выбранной урны наугад берут один шар. Найти вероятность того, что шар белый.
Обозначим: событие А – выбран белый шар, Р(А) – ?. Введем три предположения (гипотезы):
Н1 – выбран шар из I-ой урны;
Н2 – выбран шар из II-ой урны;
Н3 – выбран шар из III-ей урны.
Очевидно, эти гипотезы являются несовместными событиями, одно из которых обязательно реализуется в результате испытания, то есть
3
∑ P(H i ) = 1 .
i=1
Найдем вероятности следующих событий:
P(H1 ) = |
1 |
, P(H |
2 ) = |
1 |
, P(H |
3 ) = |
1 |
. |
|
|
|
||||||
3 |
|
3 |
|
3 |
|
|||
Р(А·Н1) = Р(Н1)Р(А/Н1), P( A / H1 ) = 7 ; 10
Р(А·Н2) = Р(Н2)Р(А/Н2), P( A / H 2 ) = 4 ; 10
Р(А·Н3) = Р(Н3)Р(А/Н3), P( A / H 3 ) = 2 . 10
24
Откуда имеем:
Р(А) = Р (АН1 + АН2 + АН3) = Р (АН1) + Р (АН2) +
+ Р (АН3) = 1 × 7 + 1 × 4 + 1 × 2 = 13 . |
||||||
3 |
10 |
3 |
10 |
3 |
10 |
30 |
Перенесем эту задачу в следующую общую ситуацию: событие А может наступить при одной из n взаимоисключающих гипотез Н1, Н2, …, Нn. Рассуждая аналогично, применяя формулы сложения, умножения событий, получаем формулу
Р(А) = Р(Н1)Р(А/Н1)+Р(Н2)Р(А/Н2) + … + Р(Нn)Р(А/Нn), (9)
которая называется формулой полной вероятности.
Вычисление вероятностей гипотез при наличии дополнительной информации. Формула Байеса.
Рассмотрим две задачи.
I |
II |
8 б |
1 б |
2 ч |
9 ч |
Рис. 8
1. Известно, что в соседней комнате проводилось следующее испытание: из наугад выбранной урны (рис. 8) брали наугад один шар. Какова вероятность того, что его брали: а) из первой урны (Н1); б) из второй урны (Н2)?
В этой ситуации оба предположения следует считать равновозможными:
P(H1 ) = P(H 2 ) = 1 . 2
2. Известно, что в соседней комнате проводилось то же испытание, и был вынут белый шар. Какова вероятность, что шар взят: а) из первой урны; б) из второй урны.
В этой ситуации гипотезы нельзя считать равновозмож-
25
ными: в первой урне значительно больше белых шаров, чем во второй. Как в этой ситуации найти вероятности гипотез?
Эта задача может быть в общем виде сформулирована так:
1)в данном испытании интересующее нас событие А может наступить при одной из n взаимоисключающих гипотез
Н1, Н2, …, Нn;
2)известно, что испытание проведено и его результат известен: наступило событие А. Как найти вероятности
Р(Н1/А), Р(Н2/А), …, Р(Нn/А)?
Утверждение. В указанной ситуации справедлива формула:
P(Hk / A) = |
P(Hk )P(A/ Hk ) |
|
|
, (10) |
|
|
||
|
P(H1)P(A/ H1) + P(H2)P(A/ H2) +K+ P(Hn)P(A/ Hn) |
|
которая называется формулой Байеса.
Доказательство. По формуле (7) имеем
Р(А·Нk) = Р(А) · Р(Нk/А), Р(А·Нk) = Р(Нk) · Р(А/Нk).
Откуда, учитывая формулу (9), получаем
P(H / A) = |
P(Hk )P(A/ Hk ) |
= |
P(Hk )P(A/ Hk ) |
|
. |
k |
P(A) |
P(H1)P(A/ H1) +K+ P(Hn )P(A/ Hn ) |
|
||
|
|
||||
§6. Схема с повторением испытаний (схема Бернулли)
Рассмотрим следующую часто встречающуюся ситуацию.
1.Проводится серия n независимых испытаний. Независимость испытаний означает, что при выполнении каждого следующего испытания полностью восстанавливается комплекс условий, при которых выполнялось предыдущее испытание.
2.При каждом испытании интересующее нас событие
А(успех) наступает с вероятностью р и не наступает с вероятностью q = 1 – p. Такую ситуацию будем называть
схемой с повторением испытаний или схемой Бернулли.
26

Обозначим через x число успехов в серии из n независимых испытаний. Очевидно, x в зависимости от
случая принимает значения |
|
0, 1, 2, …, n. |
|
Каковы вероятности этих значений? |
|
Теорема 1. Справедлива формула |
|
P(ξ = k) = Cnk p k q n−k , k = 0, 1,…, n. |
(11) |
Эта формула называется формулой Бернулли. |
|
Доказательство. |
|
P(ξ = k) = P(Y KY H KH +Y KY HYHKH +K+ H KHY KY) = |
||||||
|
123123 |
123 |
123123 |
|||
|
|
k |
n−k |
k −1 |
n−k |
k |
= P(Y KY H KH ) + P(Y KY HYHKH ) +K+ P(H KHY KY ) = |
||||||
123123 |
123 |
123123 |
||||
k |
n−k |
|
k −1 |
|
n−k |
k |
= p K pq Kq + p K pqpq Kq +K+ q Kq p K p = |
|
|||||
123123 |
123 |
|
123123 |
|
||
k |
n−k |
|
k −1 |
|
n−k k |
|
= p k q n−k + p k q n−k +K+ p k q n−k .
Здесь Y (успех) – появление события А, Н (неуспех)– непоявление события А.
Число слагаемых в этой сумме равно числу способов выбрать k мест из n свободных мест, то есть числу
сочетаний из n по k:
P(ξ = k) = Cnk p k q n−k ,
что и требовалось доказать.
Пример 1. Проводится десять независимых бросаний монеты. Найти вероятность того, что три раза из 10 выпадет герб.
Решение. Здесь успех – выпадение герба, x – число
успехов, p = q = 1 , n = 10, k =3. Следовательно, из формулы
2
(11) имеем
P(ξ = 3) = C 3 |
p 3 q10−3 = C 3 |
× |
1 |
= |
15 |
. |
|
|
|||||
10 |
10 |
210 |
128 |
|
||
Пример 2. Проводится 100 независимых бросаний монеты. Найти Р (40≤ x≤ 60), x - число выпадений герба.
27
Решение.
Р (40≤ ξ≤ 60) = Р(ξ = 40) + Р(ξ = 41) + Р(ξ = 42) + … +
+ Р(ξ = 60) = C 40 |
|
1 |
100 |
+ C 41 |
|
1 |
100 |
+ ... + C 60 |
|
1 |
100 |
|
|
|
|
|
|
|
|
. |
|||
|
|
|
|||||||||
100 |
|
2 |
|
100 |
|
2 |
|
100 |
|
2 |
|
Мы видим: если в схеме Бернулли число испытаний n велико, то подсчет вероятностей вида P(m1 ≤ ξ≤ m2) с помощью формулы Бернулли весьма затруднен.
Укажем приближенную формулу для подсчета таких вероятностей, доказанную независимо французскими математиками Муавром и Лапласом.
Для этого вначале введем функцию, которая называется функцией Лапласа и обозначается Ф(х):
|
|
1 |
|
x |
− |
t 2 |
|
|
Ф ( x ) = |
|
|
∫ e |
|
|
|
||
|
|
2 dt . |
(12) |
|||||
|
|
|
|
|||||
|
|
|
|
|||||
2π |
|
|||||||
|
|
0 |
|
|
|
|
||
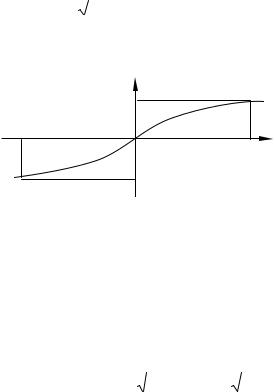
Укажем график и некоторые свойства этой функции.
Ф(x)
0,5
– 3 |
0 |
3 x |
–0,5
Рис. 9
10. Ф(0) = 0; 20. Ф (– х) = – Ф(х);
30. Если | x | ≥ 3, то Ф (х) ≈ ± 0,5 с большой точностью.
Для функции Лапласа имеются таблицы.
Теорема 2. В схеме Бернулли при достаточно большом числе испытаний справедлива приближенная формула:
|
m |
2 |
− np |
m |
− np |
|
||||||
P(m1 |
≤ ξ ≤ m2) ≈ Ф |
|
|
|
|
− Ф |
1 |
|
|
|
. (13) |
|
|
|
|
|
|
|
|
||||||
|
|
|
npq |
|
|
|
|
npq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
28
Эта формула называется интегральной формулой Муавра-Лапласа. Доказательство этой формулы приводится в §3 главы 3. Вычисления показывают, что эта формула является практически точной при n ≥ 30.
Вернемся к решению примера 2.
Решение. Здесь n =100, p = q = |
1 |
. По формуле |
|
2 |
|||
|
|
||
Муавра-Лапласа найдем |
|
|
Р (40 ≤ x ≤ 60) » Ф
10 |
|
|
|
10 |
|
|
|||
= Ф |
|
|
- Ф |
- |
|
|
|
= Ф(2) |
|
5 |
5 |
||||||||
|
|
|
|
|
|
||||
» 2 × 0,4772 = 0,9544 .
60 -100 × 1
2
100 × 1 × 1
2 2
- Ф(-2) =
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
40 -100 × |
|
|
|
|
|
|
|||
|
|
|
|
||||||||
|
- Ф |
|
|
|
|
2 |
|
|
|
= |
|
|
|
|
|
|
|
|
|||||
|
|
100 × |
1 |
|
1 |
|
|
|
|
||
|
|
|
× |
|
|
|
|
|
|
||
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
2 |
|
|
|
|
|
Ф(2) + Ф(2) = 2Ф(2) »
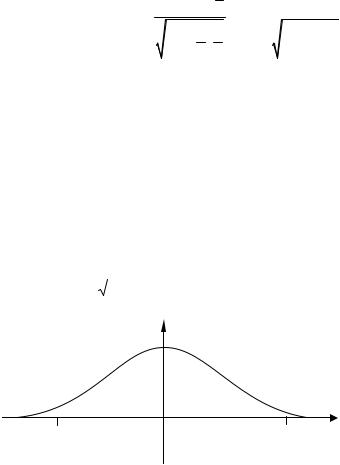
Замечание. Интегральная формула Муавра-Лапласа указывает правила вычисления вероятности неравенств вида P(m1 ≤ x ≤ m2) в схеме Бернулли при большом числе испытаний. Укажем правило вычисления вероятностей P(ξ=k) в этой ситуации.
Рассмотрим функцию
ϕ (x) = |
|
1 |
|
− |
x2 |
|
|
|
|
e 2 . |
|||||
|
|
|
|||||
2π |
|||||||
|
|
|
|
|
|
||
|
|
|
|
|
φ(х) |
||
– 3 |
0 |
3 |
x |
Рис. 10
29

Очевидно, φ(х) связана с функцией Лапласа равенством
x
Ф(x) = ∫ϕ (s)ds .
0
При большом числе испытаний справедлива приближенная формула
|
|
1 |
|
k − np |
||||
P(ξ = k) ≈ |
|
|
|
ϕ |
|
|
|
. |
|
|
|
|
|
|
|||
|
|
npq |
|
|
|
|
|
|
|
|
|
|
npq |
||||
Эта формула называется локальной формулой Лапласа. Для функции (13') имеются таблицы.
(13′ )
Муавра-
Глава 2. Случайные величины
§ 1. Дискретные и непрерывные случайные величины
Пусть с испытанием связано некоторое число, зависящее от случая. Такое число называется случайной величиной. Случайные величины будем обозначать буквами греческого алфавита: ξ, η и так далее.
Примеры случайных величин.
1.Число успехов в серии из n независимых испытаний в схеме Бернулли.
2.Число вызовов, поступающих на АТС за единицу времени.
3.Результат измерений какой-либо величины с помощью прибора.
4.Продолжительность телефонного разговора.
Случайная величина называется дискретной, если она принимает отдельные изолированные значения, и непрерывной, если ее возможные значения заполняют сплошь промежуток на числовой оси или всю числовую ось.
Очевидно, в первых двух примерах случайные величины являются дискретными, в последних двух примерах – непрерывными.
30
