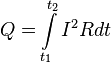Kolyas
.docx|
1 |
Кинематические характеристики движения материальной точки: перемещение, путь, траектория, скорость, ускорение |
|||||||||||||||||||
|
Кинематика-описание движения. Система отсчёта - тело отсчёта, связь с ним, система координат. Материальная точка-это любое тело, размеры которого малы по сравнению с расстояниями до других тел. Если материальная
точка свободно движется в пространстве,
то, как уже было сказано, она обладает
тремя степенями свободы (координаты
х, у иz), если она движется по некоторой
поверхности, то двумя степенями
свободы, если вдоль некоторой линии,
то одной степенью свободы.
Положение точек в пр-ве всегда описывается радиус-вектором. Перемещение – это векторная разность конечного и начального положения тела(по модулю всегда больше чем путь).
Путь – это длина участка траектории, пройденной телом или точкой тела за выбранный промежуток времени. Траектория – линия, описываемая в пространстве движущейся точкой тела (траектория движения делится на: прямолинейное, криволинейное, по окружности) Скорость – это отношение пройденного пути ко времени, за который он пройден. Она показывает, как быстро изменяется положение тела в пространстве. Вектором средней
скорости <v> называется
отношение приращения Dr радиуса-вектора
точки к промежутку времени Dt:
При неограниченном
уменьшении Dt средняя скорость
стремится к предельному значению,
которое называется мгновенной
скоростью v (первой производной
радиуса-вектора движущейся точки по
времени ):
Средняя скорость
неравномерного движения:
Ускорение – это величина, равная отношению изменения скорости движения тела к длительности промежутка времени, за которое это изменение скорости произошло. Среднее ускорениее:
Мгновенным
ускорением а (ускорением)
материальной точки в момент
времени t будет предел
среднего ускорения:
|
||||||||||||||||||||
|
2 |
Равнопеременное поступательное движение материальной точки |
|||||||||||||||||||
|
Равнопеременное движение - это такое движение, при котором материальная точка (тело) за любые равные промежутки времени изменяет свою скорость на одну и ту же величину, т.е. имеет постоянное ускорение (a=const). При поступательном движении тела все точки тела движутся одинаково, и, вместо того чтобы рассматривать движение каждой точки тела, можно рассматривать движение только одной его точки.
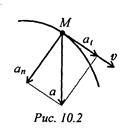
Полное ускорение равно касательному ускорению. Криволинейное равнопеременное движение (рис. 10.2):
получим значение скорости при равнопеременном движении
После интегрирования будем иметь закон равнопеременного движения в общем виде, представляющий уравнение параболы:
|
||||||||||||||||||||
|
3 |
Движение материальной точки по окружности. Связь между линейными и угловыми кинематическими характеристиками. |
|||||||||||||||||||
|
Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту). Тангенциальное
(касательное) ускорение – это
составляющая вектора ускорения,
направленная вдоль касательной к
траектории в данной точке траектории
движения.
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов
Тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная составляющая ускорения —быстроту изменения скорости по направлению (направлена к центру кривизны траектории). Для того чтобы связать линейную скорость v произвольной точки твердого тела с угловой скоростью ω вращения этого тела вокруг неподвижной оси, поделим обе части формулы на dt. Учитывая, что dr/dt=v и dφ/dt=ω, получим v=[ω,r] т.е. линейная скорость вращающейся точки равна векторному произведению угловой скорости на радиус-вектор этой точки |
||||||||||||||||||||
|
4 |
Кинематика вращательного движения твердого тела. Равнопеременное вращательное движение. |
|||||||||||||||||||
|
Поступательное движение – это такое движение, при котором любая прямая, проведенная в теле, остается параллельной самой себе. Вращательным движением абсолютно твердого тела вокруг неподвижной оси называется такое движение, при котором все точки тела описывают окружности, лежащие в параллельных плоскостях, причем центры окружностей лежат на оси вращения.
Угловая
скорость зависимость между φ – углом поворота тела и s – расстоянием, пройденным точкой тела за то же время, выражается так: s = φR. Зависимость между угловой скоростью тела и скоростью точки в каждый данный момент выражается равенством v = ωR. Касательное ускорение точки зависит от углового ускорения и определяется формулой at = εR. Нормальное ускорение точки зависит от угловой скорости тела и определяется зависимостью an = ω2R.
Вектор углового перемещения Δϕ r - это вектор, определяющий, как вращается твердое тело. Средняя угловая
скорость – это физическая величина
равная отношению вектора углового
перемещения к промежутку времени, за
который это перемещение произошло:
Мгновенная угловая скорость – это угловая скорость в данный момент времени. Векторная величина, равная первой производной от угла поворота тела по времени, называется мгновенной угловой скоростью. Среднее угловое
ускорение – это физическая величина,
равная отношению вектора изменения
угловой скорости к промежутку времени,
за который это изменение произошло: Мгновенное угловое ускорение – это физическая величина, равная отношению вектора элементарного изменения угловой скорости к промежутку времени, за который это изменение произошло.
Вращательное движение с переменной угловой скоростью называется неравномерным Если же угловое ускорение ε=const, то вращательное движение называется равнопеременным. Таким образом, равнопеременное вращение тела – частный случай неравномерного вращательного движения. Уравнение равнопеременного вращения (1)φ = φ0 + ω0t + εt2/2 и уравнение, выражающее угловую скорость тела в любой момент времени, (2)ω = ω0 + εt представляют совокупность основных формул вращательного равнопеременного движения тела. В эти формулы входят всего шесть величин: три постоянных для данной задачи φ0, ω0и ε и три переменных φ, ω и t. Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин. Просто преобразования с теми формулами: (3)φ = φ0 + (ω + ω0)t/2. (4)φ = φ0 + (ω2 - ω02)/(2ε). В частном случае равноускоренного вращения, начавшегося из состояния покоя, φ0=0 и ω0=0. Поэтому приведенные выше основные и вспомогательные формулы принимают такой вид: (5)φ = εt2/2; (6)ω = εt; (7)φ = ωt/2; (8)φ = ω2/(2ε). |
||||||||||||||||||||
|
5 |
Законы Ньютона. Инерциальная система отсчета. Принцип относительности и преобразования Галилея |
|||||||||||||||||||
Первый закон Ньютона постулирует существование инерциальных систем отсчета. Поэтому он также известен как Закон инерции. Инерция — это свойство тела сохранять скорость своего движения неизменной (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают разной инертностью. Инертность — это свойство тел сопротивляться изменению их скорости. Величина инертности характеризуется массой тела.
Замечания Когда на материальную точку действуют несколько сил, с учётом принципа суперпозиции, второй закон Ньютона записывается в виде:
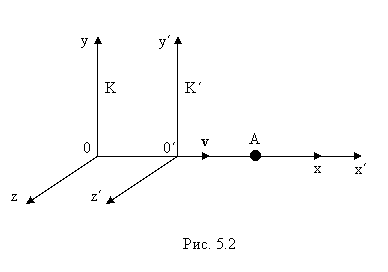
Инерциальная система отсчета - система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно или покоятся(«Инерциальной называется система отсчёта, по отношению к которой пространство является однородным и изотропным, а время — однородным») Принцип относительности – принцип, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения. Математически принцип относительности Галилея выражает инвариантность (неизменность) уравнений механики относительно преобразований координат движущихся точек (и времени) при переходе от одной инерциальной системы к другой — преобразований Галилея. Преобразования Галилея - принцип физического равноправия инерциальных систем отсчёта в классической механике, проявляющегося в том, что законы механики во всех таких системах одинаковы. Обратные и прямые преобразования Галилея
Закон сложения
скоростей. Здесь
Если система S инерциальна, то свободная частица в ней движется без ускорения, то есть, а = 0. Но ускорение такой частицы и в штрихованной системе будет отсутствовать: ведь а’ = а =0! Это означает, что она тоже является инерциальной. Сила, действующая на
частицу в системе S может
быть записана так:
А в системе штрихованной
та же сила должна быть представлена
иначе: Так как Это уравнение означает, что второй закон Ньютона не меняется при переходе в штрихованную систему отсчёта. То есть, уравнения классической механики Ньютона инвариантны относительно преобразования Галилея. В этом состоит принцип относительности Галилея, утверждающий, что все три закона динамики справедливы во всех инерциальных системах отсчёта. |
||||||||||||||||||||
|
6 |
Виды сил: гравитационная, сила тяжести, вес тела, силы упругости и трения. Основная задача механики. |
|||||||||||||||||||
|
Закон
всемирного тяготения. Все тела
притягиваются друг к другу с силой,
прямо пропорциональной их массам и
обратно пропорциональной квадрату
расстояния r между ними: Одним из проявлений закона всемирного тяготения является сила тяжести. Сила тяжести – сила, с которой нас притягивается к себе Земля . Сила тяжести направлена к центру Земли и на поверхности Земли равна:
Вблизи поверхности Земли ускорение свободного падения равно g = 9,8 м/с2. Сила, с
которой тело действует на горизонтальную
опору или подвес, называется весом
тела Сила упругости – Изменение формы или размеров тела называется деформацией. Деформации бывают упругими и пластичными. При упругих деформациях тело восстанавливает свою форму и размеры после прекращения действия силы, при пластичных – нет. При упругих деформациях справедлив закон Гука( Сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению тела и направлена противоположно направлению перемещения частиц тела относительно других частиц при деформации):
Коэффициент k называется жесткостью. Сила трения - процесс взаимодействия тел при их относительном движении. Силы, действующие между поверхностями соприкасающихся твердых тел, называются силами сухого трения. Они всегда направлены по касательной к соприкасающимся поверхностям. Сила трения покоя – величина непостоянная, она растет по модулю вместе с внешней силой от нуля до некоторого максимального значения Fтр max. Сила трения покоя равна по модулю и противоположна по направлению проекции внешней силы, направленной параллельно поверхности соприкосновения его с другим телом. Если внешняя сила больше Fтр max, то возникает движение. Силу трения в этом случае называют силой трения скольжения. Экспериментально доказано, что сила трения скольжения пропорциональна реакции опоры:
Коэффициент трения μ зависит от материалов, из которых изготовлены соприкасающиеся тела, и не зависит от размеров соприкасающихся поверхностей. Сила трения скольжения всегда направлена против относительного движения тела. При движении в жидкости или газе возникает сила вязкого трения. При вязком трении нет трения покоя. Сила вязкого трения значительно меньше силы сухого трения и также направлена в сторону, противоположную относительной скорости тела. Зависимость от модуля скорости может быть линейной F = –βυ или квадратичной F = –αυ2. Основная задача механики – определить положение тел в пространстве в любой момент времени Разделы механики: КИНЕМАТИКА - раздел механики, изучающий способы описания движений и связь между величинами, характеризующими эти движения. СТАТИКА - раздел механики, изучающий равновесие абсолютно твердых тел. ДИНАМИКА - раздел механики, изучающий взаимное влияние тел друг на друга и изменение характера движения этих тел в результате взаимодействий тел. |
||||||||||||||||||||
|
7 |
Закон сохранения импульса. Центр инерции механической системы. Абсолютно неупругий удар. |
|||||||||||||||||||
|
Закон сохранения импульса - векторная сумма импульсов всех тел (или частиц) системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю.
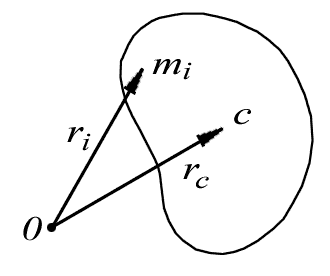
Центр
инерции (центр масс) - геометрическая
точка, характеризующая движение тела
или системы частиц как целого.
Центр масс является точкой
приложения вектора импульса системы
где
Абсолютно неупругий удар – это столкновение двух тел, в результате которого тела объединяются и двигаются дальше, как единое целое.
Если шары движутся навстречу друг другу, то они вместе будут продолжать двигаться в ту сторону, в которую двигался шар, обладающий большим импульсом. В частном случае, если массы шаров равны (т1=т2), то
Выясним,
как изменяется кинетическая энергия
шаров при центральном абсолютно
неупругом ударе. Так как в процессе
соударения шаров между ними действуют
силы, зависящие не от самих деформаций,
а от их скоростей, то мы имеем дело с
силами, подобными силам трения, поэтому
закон сохранения механической энергии
не должен соблюдаться. Вследствие
деформации происходит «потеря»
кинетической энергии, перешедшей
в тепловую или другие формы
энергии. Эту «потерю» можно определить
по разности кинетической энергии тел
до и после удара:
|
||||||||||||||||||||
|
8 |
Работа и энергия. Работа переменной силы. Мощность. Работа консервативных сил. Потенциальная энергия в поле сил тяжести, упругости и тяготения. |
|||||||||||||||||||
|
Работа
- физическая величина, равная
произведению силы, перемещения и
косинуса угла между направлением
действия силы и перемещением:
Энергия
является мерой способности физической
системы совершить работу, поэтому
количественно энергия и работа
выражаются в одних единицах.
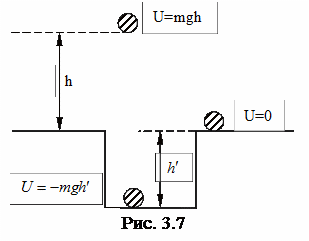
Из предыдущего уравнения вытекает, что работа не зависит от траектории движения в доле силы тяжести, а определяется лишь изменением высоты. Потенциальная энергия характеризует и другие взаимодействующие тела. Так, потенциальной энергией обладает сжатая пружина:
где k - модуль упругости, х - смещение от положения равновесия. Потенциальная энергия, как и кинетическая, является величиной относительной, поскольку и высота, и смещение зависят от выбора точки отсчета.
Работа
переменной силы - Всю траекторию
мысленно разбивают на отдельные
участки такой малой длины |dr|, что
действующую на них силу можно считать
постоянной.
Мощность - физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
где F —
сила, v —
скорость,
Для пассивной линейной цепи, в которой соблюдается закон Ома, можно записать:
Мгновенной мощностью называется скалярная величина, равная отношению элементарной работы к промежутку времени, за который она была совершена Консервативные силы - это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения и определяется только начальным и конечным положением этой точки
Работа совершается из-за убыли потенциальной энергии. Потенциальная
энергия в поле сил тяжести – Работа
силы тяжести равна изменению
потенциальной энергии тела, взятому
с противоположным знаком
Потенциальная
энергия упруго деформированного
тела равна работе силы упругости
при переходе из данного состояния в
состояние с нулевой деформацией.
Так,
для груза весом G,
поднятого на высоту h,
потенциальная энергия будет
равна: |
||||||||||||||||||||
|
9 |
Закон сохранения полной механической энергии. Абсолютно упругий удар. |
|||||||||||||||||||
|
Закон
сохранения полной механической
энергии –
Абсолютно упругий удар – такой удар, при котором полная кинетическая энергия системы сохраняется
|
||||||||||||||||||||
|
|
|
|||||||||||||||||||
|
10 |
Динамика вращательного движения твердого тела. Динамические характеристики вращательного движения: момент силы, момент импульса, момент инерции. Уравнение моментов. |
|||||||||||||||||||
|
Момент
силы
— векторная физическая величина,
равная произведению радиус-вектора,
проведенного от оси вращения к точке
приложения силы, на вектор этой силы.
Характеризует вращательное действие
силы на твёрдое тело.
F – Сила действующая на тело. r – Плечо силы.
Моментом импульса материальной точки относительно оси вращения называется вектор L, равный векторному произведению радиуса-вектора r на вектор импульса P: L = [ r∙P] = [ r∙ mv], где m, v -
соответственно масса и вектор скорости
точки. Направление Lопределяется по
правилу правого буравчика. Модуль
вектора L = mv∙ r∙ sinα, где α - угол между
векторами r и v.
Па́ра сил — совокупность двух сил, которые приложены к одному абсолютно твёрдому телу и при этом равны по модулю и противоположны по направлению. Моментом инерции материальной точки относительно оси вращения называется физическая величина, численно равная произведению массы точки на квадрат расстояния точки до оси вращения .
Момент инерции - величина скалярная. Моментом инерции механической системы относительно неподвижной оси называется физическая величина, равная сумме произведений масс всех точек системы на квадраты их расстояний до оси вращения. I = mi∙ ri2 Для твердого тела, разбитого на элементарные массы ∆ mi, момент инерции относительно оси равен I = ∆ mi∙ ri2. Обруч:
Основное
уравнение динамики вращательного
движения тела можно представить в
виде Последнее уравнение можно записать в более общем виде:
|
||||||||||||||||||||
|
11 |
|
|||||||||||||||||||
|
|
||||||||||||||||||||
|
12 |
Теорема штейнера |
|||||||||||||||||||
|
момент
инерции тела I относительно
произвольной оси равен сумме момента
инерции этого тела IС относительно
параллельной ей оси, проходящей через
центр масс тела, и произведения массы
тела на квадрат расстояния между
осями:.
. Обруч:
|
||||||||||||||||||||
|
13 |
Основной закон динамики вращательного движения |
|||||||||||||||||||
|
Основной закон динамики вращательного движения можно получить из второго закона Ньютона для поступательного движения твердого тела
где Если к
твердому телу массой m в
точке А (рис. 5) приложить силу
где mi –
масса i-й точки; Умножая левую и правую части уравнения (1.7) на ri, получают
где Плечом
силы называют кратчайшее расстояние
от оси вращения “ОО” (рис. 5) до
линии действия силы
Выражение (1.8) можно записать так:
Просуммируем левую и правую части (1.9) по всем точкам тела:
Обозначим
Уравнение
(1.10) – основной закон динамики
вращательного движения твердого
тела. Величина Мгновенное
значение углового ускорения
где Если в выражение основного закона (1.10) поставить значение мгновенного ускорения (1.11), то
где
Поэтому
основной закон динамики вращательного
движения твердого тела формулируется
так: “Импульс момента силы
|
||||||||||||||||||||
|
14 |
Работа и энергия при вращательном движении. Плоское движение твердого тела. Полная энергия тела, катящегося без скольжения. |
|||||||||||||||||||
|
Если твердое
тело движется поступательно со
скоростью v и одновременно
вращается с угловой скоростью ω вокруг
оси, проходящей через его центр
инерции, то его кинетическая энергия
определяется как сумма двух составляющих:
При повороте
тела на бесконечно малый угол dφ точка
приложения В проходит путь ds =
rdφ, и работа равна произведению
проекции силы на направление смещения
на величину смещения: dA = Fsinα*rdφ
Плоским (плоскопараллельным)
назыв. такое движение, при котором
все его точки перемещаются параллельно
некоторой неподвижной плоскости :
Плоского
движения тела, например цилиндра,
скатывающегося
с наклонной плоскости без скольжения.
Его энергия движения складывается
из энергии поступательного движения
и энергии вращения:
|
||||||||||||||||||||
|
15 |
Собственные незатухающие гармонические колебания- амплитуда которых не меняется во времени. Такие колебания называются собственными незатухающими x = A cos
(ω0t + 0)
6. Частота колебаний 0 число полных колебаний, совершаемых в одну секунду
7. Скорость колеблющегося тела v = dx/dt
8. Ускорение
колеблющегося тела v =
d2x/dt2 =
dv/dt
9. Сила F = kx
т.е. период и фаза силы и ускорения совпадают. 10. Полная энергия незатухающих колебаний
Векторное представление гармонических функций, частота которых одинакова, облегчает операции сложения и вычитания этих функций. Ввиду того, что сумма проекций двух векторов равна проекции геометрической суммы этих векторов, амплитуда и начальная фаза результирующей кривой легко находятся из векторной диаграммы геометрическим сложением векторов.
|
|||||||||||||||||||
|
|
||||||||||||||||||||
|
16 |
Кинематические характеристики материальной точки участвующей в гармонических колебаниях: смещение, скорость, ускорение. Уравнение гармонических колебаний. Полная энергия колеблющейся точки. |
|||||||||||||||||||
|
Гармоническими называются колебания, для которых изменяющаяся величина зависит от времени по закону синуса или косинуса. Уравнение гармонических колебаний можно записать в виде: x = A*sin(wt + f0), где x - смещение точки от положения равновесия, A - амплитуда колебаний, (wt+f0) - фаза колебаний, f0 - начальная фаза, w - частота, t - время. Скорость гармонического колебания Ускорение
колеблющейся точки При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией. Кинетическая энергия тела W:
|
||||||||||||||||||||
|
17 |
Математический и физический маятники. Период и приведенная длина физического маятника. |
|||||||||||||||||||
|
Математический маятник. Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.
Таким
маятником можно считать тяжелый шар
массой m, подвешенный на тонкой нити,
длина l которой намного больше размеров
шара. Если его отклонить на угол α
(рис.7.3.) от вертикальной линии, то под
влиянием силы F – одной из составляющих
веса Р он будет совершать колебания.
Другая составляющая
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
Момент
силы относительно точки О:
С
учетом этих величин имеем:
или
Его
решение
Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний. Физический маятник. Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.
При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
Решение
этого уравнения
Определим
длину l математического маятника, при
которой период его колебаний равен
периоду колебаний физического
маятника, т.е.
Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.
|
||||||||||||||||||||
|
18 |
Собственные Затухающие Колебания. Уравнение колебаний. Период и частота затухающих колебаний. Постоянная затухания, логарифмический декремент, и добротность затухающих колебаний. |
|||||||||||||||||||
|
Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины. Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими. Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения
где r - коэффициент сопротивления среды. Знак минус показывает, что FC направлена в сторону противоположную скорости. Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r. По второму закону Ньютона
где β - коэффициент затухания(постоянная затухания). Этот коэффициент характеризует скорость затухания колебаний, При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать.
- дифференциальное уравнение затухающих колебаний.
- уравнение затухающих колебаний. ω – частота затухающих колебаний:
Период затухающих колебаний:
Затухающие
колебания при строгом рассмотрении
не являются периодическими. Поэтому
о периоде затухаюших колебаний можно
говорить, когда β мало. Если
затухания выражены слабо (β→0), то рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону
В уравнении (1) А0 и φ0 - произвольные константы, зависящие от выбора момента времени, начиная е которого мы рассматриваем колебания
Рассмотрим колебание в течение, некоторого времени τ, за которое амплитуда уменьшится в е раз
τ - время релаксации. Коэффициент затихания β обратно пропорционален времени, в течение которого амплитуда уменьшается в е раз. Однако коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затуханияD, который равен отношению амплитуд, отстоящих по времени на период:
Логарифмический декремент затухания равен логарифму D:
Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний уменьшилась в е раз. Логарифмический декремент затухания - постоянная для данной системы величина. Еще одной характеристикой колебательной система является добротность Q.
Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ. Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии. Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.
Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим. |
||||||||||||||||||||
|
19 |
Параметры термодинамического состояния: давление, объем, температура. Идеальный газ. Уравнение состояния идеального газа. |
|||||||||||||||||||
|
В технической термодинамике основными параметрами состояния являются термические параметры: абсолютное давление (р), температура (Т) и удельный объем (v). Давление – сила, действующая нормально к площади. p = F/ где F – сила, действующая нормально к площади; f – площадь. В международной системе единиц (СИ) имеет размерность p = 1Н/1м2 = 1 Па. Паскаль равен давлению, вызываемому силой 1н по нормали к поверхности в 1 м2. Все технические приборы, измеряющие давление, показывают избыточное давление Ризб. Избыточное давление – это разность между давлением в термодинамической системе (абсолютное давление) и внешним атмосферным давлением В. Термодинамика оперирует только с абсолютным давлением в термодинамической системе, которое равно Pабс = Ризб + В, (1.2) Рабс = В – Рвак (1.3)где Ризб – избыточное давление; B – атмосферное давление; Рабс – абсолютное давление; Рвак – величина вакуума (разряжения) формулы (1.2) используется при давлениях больше атмосферного, а формула (1.3) – при давлениях меньше атмосферного. Температура – одна из основных величин в технической термодинамике. Принцип измерения температуры основан на очевидном законе логики. Если два тела в отдельности находятся в тепловом равновесии с третьим телом, то все три тела находятся в тепловом равновесии, а значит имеют одинаковую температуру. Следовательно, по показанию термометра можно сравнить температуру разных тел. Для измерения температуры используют технические приборы: термометры, термопары, термометры сопротивления и др. В каждом из этих приборов используется зависимость какого-либо физического свойства (коэффициента объемного расширения, удельного сопротивления, электродвижущей силы) от температуры. Определение температуры при помощи таких приборов зависит от индивидуальных свойств термодинамического вещества (чувствительного элемента термометра), так как одна и та же физическая величина имеет разную зависимость от температуры для различных материалов. Абсолютная температура (не зависит от свойств термометрического вещества) определяется с помощью идеального газового термометра, что следует из Второго закона термодинамики. Это впервые показал Кельвин и в его честь эта абсолютная (термодинамическая температура) была названа температурой Кельвина. Термодинамическая температура по Второму закону не может иметь отрицательных значений, а нулевая точка равна наинизшей термодинамически возможной температуре – абсолютному нулю. Единицей измерения температуры в Международной системе единиц (СИ) является градус Кельвина – К: Т, К = t˚C + 273,15 Удельный объем, как температура и давление, являются термодинамическим параметром. Удельный объем (v) – величина, равная отношению объем V однородного тела к его массе: v = V/m = 1/ρ Размерность удельного объема в Международной системе СИ (м3/кг). Эта величина обратно пропорциональна плотности (ρ). В термодинамике удобно рассматривать не плотность, а удельный объем, так как многие термодинамические системы имеют настоящую массу и тогда удельный объем пропорционален общему объему. В термодинамике широко распространено понятие о количестве вещества «n». Во времена Ньютона количество вещества отождествлялось с массой. В современной метрологии количеством вещества называется число атомов, молекул, ионов или, как говорят, число структурных элементов, из которых состоит вещество. Но число частиц тела макроскопических размеров велико (N ≈ 1025). Поэтому вводится величина пропорциональная числу частиц, которая получила название количества вещества. n = N/Na, где Na – универсальная газовая постоянная или число Авогадро. Количество вещества относится к категории основных в системе СИ и получила наименование моля при следующем определении: моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится в углероде-12 массой 0,012 кг. Из формулы видно, что число Авогадро выражает число молекул или других частиц, содержащихся в одном моле вещества. Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями. В расширенной модели идеального газа частицы, из которого он состоит, имеют также форму в виде упругих сфер или эллипсоидов, что позволяет учитывать энергию не только поступательного, но и вращательно-колебательного движения, а также не только центральные, но и нецентральные столкновения частиц и др. На основании обобщения экспериментальных данных было получено соотношение, связывающее основные макроскопические параметры состояния газа:
Это уравнение называется уравнением состояния идеального газа или уравнением Менделеева - Клапейрона.
Введя
новую фундаментальную постоянную
Давление смеси идеальных газов подчиняется закону Дальтона, в соответствии с которым это давление равно сумме парциальных давлений, входящих в нее газов
|
||||||||||||||||||||
|
20 |
Основное уравнение мкт |
|||||||||||||||||||
|
|
||||||||||||||||||||
|
|
||||||||||||||||||||
|
Пусть
имеется кубический сосуд с ребром
длиной Обозначим
скорость движения Отсюда следует:
Так как
давление Подставив,
получим: Преобразовав: Так как
рассматривается кубический сосуд,
то Отсюда:
Соответственно, Таким
образом, для большого числа частиц
верно следующее: Поскольку Отсюда или Пусть
|
||||||||||||||||||||
|
21 |
Идеальный газ в поле силы тяжести |
|||||||||||||||||||
|
Барометрическая
формула — зависимость давления
или плотности газа от высоты в поле
тяжести. Для идеального газа, имеющего
постоянную температуру T и находящегося
в однородном поле тяжести (во всех
точках его объёма ускорение свободного
падения g одинаково), барометрическая
формула имеет следующий вид:
,
где p — давление газа в слое,
расположенном на высоте h, p0 —
давление на нулевом уровне (h = h0),
z=h-h0
- координата(высота) точки по отношению
к уровню, принятому за нулевой, m
- масса частицы, M — молярная масса
газа, R — газовая постоянная, T —
абсолютная температура. Из барометрической
формулы следует, что концентрация
молекул n (или плотность газа) убывает
с высотой по тому же закону:
где
M — молярная масса газа, R —
газовая постоянная. Барометрическая
формула показывает, что плотность
газа уменьшается с высотой по
экспоненциальному закону. Величина
определяющая
быстроту спада плотности, представляет
собой отношение потенциальной энергии
частиц к их средней кинетической
энергии, пропорциональной kT. Чем выше
температура T, тем медленнее убывает
плотность с высотой. С другой стороны,
возрастание силы тяжести mg (при
неизменной температуре) приводит к
значительно большему уплотнению
нижних слоев и увеличению перепада
(градиента) плотности. Действующая
на частицы сила тяжести mg может
изменяться за счёт двух величин:
ускорения g и массы частиц m. Следовательно,
в смеси газов, находящейся в поле
тяжести, молекулы различной массы
по-разному распределяются по высоте.
Пусть идеальный газ находится в поле
консервативных сил в условиях теплового
равновесия. При этом концентрация
газа будет различной в точках с
различной потенциальной энергией,
что необходимо для соблюдения условий
механического равновесия. Так, число
молекул в единичном объеме n убывает
с удалением от поверхности Земли, и
давление, в силу соотношения P = nkT,
падает. Если известно число молекул
в единичном объеме, то известно и
давление, и наоборот. Давление и
плотность пропорциональны друг другу,
поскольку температура в нашем случае
постоянна. Давление с уменьшением
высоты должно возрастать, потому что
нижнему слою приходится выдерживать
вес всех расположенных сверху атомов.
Исходя из основного уравнения
молекулярно-кинетической теории: P =
nkT, заменим P и P0 в барометрической
формуле (2.4.1) на n и n0 и получим
распределение Больцмана для молярной
массы газа:
где n0
и n - число молекул в единичном объёме
на высоте h = 0 и h.
представить в виде
С уменьшением температуры число молекул на высотах, отличных от нуля, убывает. При T = 0 тепловое движение прекращается, все молекулы расположились бы на земной поверхности. При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой. Так как mgh – это потенциальная энергия U, то на разных высотах U = mgh – различна. Следовательно, (2.5.2) характеризует распределение частиц по значениям потенциальной энергии:
–
это
закон распределения частиц по
потенциальным энергиям – распределение
Больцмана. Здесь n0 – число молекул в
единице объёма там, где U = 0(потенциальная
энергия). На рисунке показана зависимость
концентрации различных газов от
высоты. Видно, что число более тяжелых
молекул с высотой убывает быстрее,
чем легких.
|
||||||||||||||||||||
|
22 |
Внутренняя энергия идеального газа |
|||||||||||||||||||
|
Исходя из определения идеального газа, в нем отсутствует потенциальная составляющая внутренней энергии (отсутствуют силы взаимодействия молекул, кроме ударного). Таким образом, внутренняя энергия идеального газа представляет собой только кинетическую энергию движения его молекул.( Внутренняя энергия любого вещества (в том числе и газа) - это сумма кинетических и потенциальных энергий всех молекул. Идеальный газ - это модель реального газа, в которой молекулы принимаем за материальные точки (т. е. не учитываем размеры молекул) и пренебрегаем взаимодействием молекул друг с другом. Поэтому внутренняя энергия идеального газа равна только сумме кинетических энергий молекул (потенциальная энергия взаимодействия молекул равна 0). У реального газа потенциальная энергия взаимодействия молекул не равна 0, и она вносит вклад в выражение для внутренней энергии). Кинетическая энергия поступательного движения молекул газа прямо пропорциональна его абсолютной температуре
Используя выражение универсальной газовой постоянной (4.6), можно определить величину константы α
Таким образом, кинетическая энергия поступательного движения одной молекулы идеального газа будет определяться выражением
В соответствии с кинетической теорией, распределение энергии по степеням свободы равномерное. У поступательного движения 3 степени свободы. Следовательно, на одну степень свободы движения молекулы газа будет приходиться 1/3 ее кинетической энергии
Для двух, трех и многоатомных молекул газа кроме степеней свободы поступательного движения есть степени свободы вращательного движения молекулы. Для двухатомных молекул газа число степеней свободы вращательного движения равно 2, для трех и многоатомных молекул - 3. Поскольку распределение энергии движения молекулы по всем степеням свободы равномерное, а число молекул в одном киломоле газа равняется Nμ, внутреннюю энергию одного киломоля идеального газа можно получить, умножив выражение (4.11) на число молекул в одном киломоле и на число степеней свободы движения молекулы данного газа
где Uμ - внутренняя энергия киломоля газа в Дж/кмоль(берем молярный объем), для произвольного количества газа
i - число степеней свободы движения молекулы газа, определяющие структуру молекул(минимальное число параметров, которые полностью определяют положение тела в пространстве в выбранной системе отсчета: x, y, z - центр масс, альфа, бета, гамма - вращательные параметры (всего 6 степеней свободы) i=n(поступат)+n(вращат) на каждую степень свободы приходится Е1=1/2 * kT(внутренняя энергия) Для 1-атомного газа i = 3, для 2-атомного газа i = 5, для 3-атомного и многоатомного газов i = 6. Для многоатомного газа i=6, так как существуют 3 степени свободы поступательного движения и 3 степени свободы вращательного движения молекул. Может быть еще колебательное движение атомов в молекуле, но его обычно учитывают для реальных газов, используя экспериментальные данные. Для идеальных газов колебательное движение атомов в молекулах тоже может быть учтено при расчете внутренней энергии, об этом будет сказано в разделе "Зависимость теплоемкостей идеальных газов от температуры". На данном этапе изложения материала будем руководствоваться молекулярно-кинетической теорией идеального газа. В соответствии с ней атомы в молекулах идеального газа имеют жесткие связи, т.е. колебательного движения атомов в молекулах нет. Для одного килограмма идеального газа удельная внутренняя энергия в Дж/кг определяется делением выражения (4.12) на молярную массу газа
Для произвольного количества газа внутренняя энергия определяется как произведение его массы на удельную внутреннюю энергию этого газа
где m - масса газа в кг, U - полная внутренняя энергия идеального газа. Если система состоит из нескольких различных по физическим свойствам газов, то, подчиняясь закону сложения (аддитивности), его полная внутренняя энергия будет определяться суммой внутренних энергий компонентов газовой смеси
где n - число компонентов газа в системе. Полученные уравнения внутренней энергии идеального газа (4.12) - (4.15) указывают на то, что внутренняя энергия идеального газа зависит только от абсолютной температуры газа и числа степеней свободы движения его молекул
или
|
||||||||||||||||||||
|
23 |
Работа и теплота в термодинамич. процессах |
|||||||||||||||||||
|
энергия, Передаваемая рассматриваемой термодинамической системе внешними телами, называется работой, совершаемой над системой Теплота – это энергия, передаваемая системе внешними телами путем теплообмена. первое начало термодинамики: (количество теплоты , полученное системой, идет на изменение ее внутренней энергии и совершение работы против внешних сил).
Для равновесных процессов: сигмаQ=dU+pdV, если dU=0, то сигмаQ=сигмаА; сигмаQ=dU+сигмаА, если dU=0, dQ=0, то сигмаА=0, следовательно вечный двигатель первого рода невозможен. В любой изолированной системе запас энергии остается постоянным.
теплота, сообщаемая системе, расходуется на изменение внутренней энергии системы и на совершение системой работы против внешних сил (сигма)Q = dU + (сигма)А
Теплоемкость –количество тепла, необходимое чтобы нагреть тело на 1К или 1⁰С
(бесконечно малое количество теплоты полученное телом к приращению его температуры) Существуют удельная, молярная и объемные теплоемкости. Удельна С- количество тепла, необходимое чтобы нагреть тело массой 1кг на 1К или 1⁰С (Дж/кг К)
Молярная С- количество тепла, необходимое чтобы нагреть тело в количестве 1 моль на 1К или 1⁰С(Дж/моль К) , где υ-моль
С=с*M - взаимосвязь теплоемкостей, где М- молярная масса вещества
Моль- количество вещества, которое содержит столько же структурных единиц, сколько содержится атомов в 12гр в изотопе С(12)-углерод. Нормальные условия( t=0⁰C, p=1атм)
Теплоемкости при постоянном объёме (Cv) и при постоянном давлении (Ср), если в процессе нагревания поддерживаются постоянными соответственно его объём или давление. При нагревании при постоянном давлении часть теплоты идёт на производство работы расширения тела, а часть — на увеличение его внутренней энергии. Сp>Cv всегда Сp=Cv+R
Среди
равновесных процессов, которые
происходят с термодинамическими
системами, отдельно рассматриваются
изопроцессы, при которых один из
основных параметров состояния остается
постоянным.
Изохорный
процесс (V=const). Диаграмма этого
процесса (изохора) в координатах
р, V изображается прямой, параллельной
оси ординат (рис. 1), где процесс 1—2
есть изохорное нагревание, а 1—3 —
изохорное охлаждение. При изохорном
процессе газ не совершает работы над
внешними телами, т. е.
В изобарном
процессе при сообщении газу массой
m количества теплоты
Значит, для того чтобы при расширении газа температура не становилась меньше, к газу в течение изотермического процесса необходимо подводить количество теплоты, равное внешней работе расширения. |
||||||||||||||||||||
|
24 |
адиабатический процесс - процесс, при котором физ. система не получает теплоты извне и не отдаёт её.(Q=0) Изолированный процесс от внешних энергий уравнение
адиабаты
При разряжении V увелич, а Р уменьшается, то Т уменьш
или
где γ = Cp/Cv— показатель адиабаты (для воздуха γ = 1,4). (сигма) Из
первого закона термодинамики следует,
что при адиабатном процессе работа
производится только за счет изменения
внутренней энергии вещества:
Работа при адиабатическом процессе:
|
|||||||||||||||||||
|
|
||||||||||||||||||||
|
25 |
Кпд
1.
2. где А — полезная работа, а Q — затраченная энергия, тепло, передаваем телу от нагревателя. Вечный двигатель второго рода невозможен(когда Q2=0).
3.
Принцип действия - Большая часть двигателей на Земле - это тепловые двигатели. Устройства, превращающие энергию топлива в механическую энергию, называются тепловыми двигателями. Любой тепловой двигатель (паровые и газовые турбины, двигатели внутреннего сгорания) состоит из трех основных элементов: рабочего тела (это газ), которое совершает работу в двигателе; нагревателя, от которого рабочее тело получает энергию, часть которой затем идет на совершение работы; холодильника, которым является атмосфера или специальные устройства. Ни один тепловой двигатель не может работать при одинаковой температуре его рабочего тела и окружающей среды. Обязательно температура нагревателя больше температуры холодильника. При совершении работы тепловыми двигателями происходит передача теплоты от более горячих тел к более холодным. Рабочее тело двигателя получает количество теплоты QН от нагревателя, совершает работу A' и передает холодильнику количество теплоты Q. В соответствии с законом сохранения энергии А' < QН - QХ. В случае равенства речь идет об идеальном двигателе, в котором нет потерь энергии. Отношение работы к энергии, которое получило рабочее тело от нагревателя, называют коэффициентом полезного действия (КПД): < 1. В процессе работы многочисленных тепловых машин возникают тепловые потери, которые в конечном счете приводят к повышению внутренней энергии атмосферы, т. е. к повышению ее температуры. Это может привести к таянию ледников и катастрофическому повышению уровня Мирового океана, а вместе с тем к глобальному изменению природных условий. При работе тепловых установок и двигателей в атмосферу выбрасываются вредные для человека, животных и растений оксиды азота, углерода и серы. С вредными последствиями работы тепловых машин можно бороться путем повышения КПД, их регулировки и создания новых двигателей, не выбрасывающих вредные вещества с отработанными газами.
|
|||||||||||||||||||
|
Теплова́я маши́на — устройство, преобразующее тепловую энергию в механическую работу (тепловой двигатель) или механическую работу в тепло (холодильник). Преобразование осуществляется за счёт изменения внутренней энергии рабочего тела — на практике обычно пара или газа.
Тепловая машина- периодич действующ устройство, по замкнутому циклу, преобразов тепло от нагревателя для совершения работы(по часовой стрелке положит работа) Тепловыми маши́нами в термодинамике называются тепловые двигатели и холодильные машины (термокомпрессоры)
|
||||||||||||||||||||
|
26 |
Цикл Карно. КПД идеальной тепловой машины, работающей по циклу Карно. Теорема Карно. |
|||||||||||||||||||
|
цикл Карно́ или процесс Карно — это обратимый круговой процесс, состоящий из двух адиабатических и двух изотермических процессов[1]. В процессе Карно термодинамическая система выполняет механическую работу и обменивается теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником[
КПД идеальной тепловой машины Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно
Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику
Отсюда коэффициент полезного действия тепловой машины Карно равен
Карно теорема, теорема о коэффициенте полезного действия тепловых двигателей,установленная Н. Л. С.Карно в 1824. Согласно К. т., кпд Карно цикла не зависит от природы рабочего вещества и конструкции теплового двигателя и определяется только температурами нагревателя и холодильника. К. т. сыграла важную роль в установлении второго начала термодинамики. 2) В теории удара — теорема о потере кинетической энергии при абсолютном неупругом ударе. Названа по имени Л. Н. Карно. Кинетическая энергия, потерянная системой при ударе, равна той кинетической энергии, которую имела бы система, если бы её точки двигались с потерянными скоростями, т. е.
где
|
||||||||||||||||||||
|
27 |
Для подсчета приведенной теплоты в
произвольном процессе необходимо
разбить этот процесс на бесконечно
малые участки, где Т можно
считать константой. Приведенная
теплота на таком участке будет равна
Функция
состояния, полный дифференциал которой
равен
Энтропия S – это отношение полученной или отданной теплоты к температуре, при которой происходил этот процесс. Для обратимых процессов изменение энтропии:
Разность энтропий двух равновесных состояний: количество привед тепла, которое необходимо сообщить системе, чтобы из сост 1 в сост 2 перевести по произвольному пути(равновесно)
Понятие энтропии впервые введено Р. Клаузиусом в 1854 г. ПРИНЦИП ВОЗРАСТАНИЯ ЭНТРОПИИ сводится к утверждению, что энтропия изолированных систем неизменно возрастает при всяком изменении их состояния и остается постоянной лишь при обратимом течении процессов. Энтропия постоянна при адиабатном процессе, она увеличиваетсяпри нагревании, при охлаждении тела - уменьшается, её называют тепловым показателем. Формула Больцмана позволяет дать статистическое истолкование второго закона термодинамики, утверждающего, что энтропия изолированной системы не убывает: термодинамическая вероятность состояния изолированной системы при всех происходящих в ней процессах не может убывать. Следовательно, при всяком процессе, протекающем в изолированной системе, изменение термодинамической вероятности её состояния (дельта)Р положительно или равно нулю:
(дельта)Р=Р2–P1>=0 (11.28). Для обратимого процесса (дельта)P=0 и Р=const, а в случае необратимого процесса (дельта)Р>0 и Р возрастает.
|
|||||||||||||||||||
|
|
||||||||||||||||||||
|
28 |
Электрическое поле-особый вид материи, который недоступен нашему вниманию и проявляет себя во взаимодействии зарядов
Электростаика-изучение взаимодействия зарядов в неподвиж системах отсчета
Закон Кулона(основной закон электростатики): сила взаимодействия двух точечных зарядов(формой можно пренебречь) в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
Где k-коэф пропорциональности, k=9*10^9 м/Ф ε0=8,85*10^(-12) Ф/м - электрич постоянная
Физическая величина, равная отношению силы, с которой электрическое поле действует на точечный электрический заряд, к значению этого заряда, называется напряженностью электрического поля. Напряженность- силовая характеристика(векторная), численно равная силе, децствующей на единичный пробный заряд, помещенный в данную точку поля. Напряженность электрического поля не зависит от количества пробного заряда q
Обозначив напряженность буквой Е , запишем
где q1— заряд, на который действует сила F.
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||
|
29 |
Поток вектора напряженности … теорема Гаусса |
|||||||||||||||||||
|
Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности NE.
Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным (рис.13.4).
Поток напряженности через такую элементарную площадку будет равен по определению(рис.13.5).
где
2) Поток вектора напряженности Е электрического поля а) поток вектора напряженности через плоскую поверхность, помещенную в однородное электрическое поле, ФE=ЕScosa (5) б) поток вектора напряженности через произвольную поверхность S, помещенную в неоднородное поле
Или где a — угол между вектором напряженности Е и нормальюn к элементу поверхности; dS — площадь элемента поверхности; En — проекция вектора напряженности на нормаль; в) поток вектора напряженности Е через замкнутую поверхность
где интегрирование ведется по всей поверхности. теоремы Гаусса: поток вектора напряженности поляпо любой замкнутой поверхности пропорционален алгебраической сумме зарядов, заключенной в этой поверхности. Теорему Гаусса можно записать и для потока вектора напряженности электрического поля: Воображаемую поверхность S проводника в E любая, причем выбираем поверхность так, что Е во всех точках поверхности постоянна. Линия Е проходит по нормали поверхности, тк в противном случае заряды придут в движение.
Из теоремы Гаусса следует важное свойство электрического поля: силовые линии начинаются или заканчиваются только на электрических зарядах или уходят в бесконечность. Еще раз подчеркнем, что, несмотря на то, что напряжённость электрического поля E и электрическая индукция D зависят от расположения в пространстве всех зарядов, потоки этих векторов через произвольную замкнутую поверхность S определяются только теми зарядами, которые расположены внутри поверхности S. Дифференциальная форма теоремы Гаусса. Отметим, что интегральная форма теоремы Гаусса характеризует соотношения между источниками электрического поля (зарядами) и характеристиками электрического поля (напряженностью или индукцией) в объеме V произвольной, но достаточной для формирования интегральных соотношений, величины. Производя деление объема Vна малые объемы Vi , получим выражение
справедливое как в целом, так и для каждого слагаемого. Преобразуем полученное выражение следующим образом:
и рассмотрим предел, к которому стремится выражение в правой части равенства, заключенное в фигурных скобках, при неограниченном делении объема V. В математике этот предел называют дивергенцией вектора (в данном случае вектора электрической индукции D):
Дивергенция вектора D в декартовых координатах:
Таким образом выражение (1.7) преобразуется к виду:
Учитывая, что при неограниченном делении сумма в левой части последнего выражения переходит в объемный интеграл, получим
Полученное соотношение должно выполняться для любого произвольно выбранного объема V. Это возможно лишь в том случае, если значения подынтегральных функций в каждой точке пространства одинаковы. Следовательно, дивергенция вектора D связана с плотностью заряда в той же точке равенством
или для вектора напряженности электростатического поля
Эти равенства выражают теорему Гаусса в дифференциальной форме. Отметим, что в процессе перехода к дифференциальной форме теоремы Гаусса получается соотношение, которое имеет общий характер:
Выражение называется формулой Гаусса - Остроградского и связывает интеграл по объему от дивергенции вектора с потоком этого вектора сквозь замкнутую поверхность, ограничивающую объем. Теорема Гаусса в интегральной форме
Пусть
n – единичная нормаль к площадке dS
(достаточно малой, чтобы пренебречь
изменением электрической напряженности
Е в пределах площадки). Поток
dФэ электрической
напряженности через эту площадку
определяется как произведение
нормальной компоненты Е и dS:
Знак
потока dFэ, очевидно,
зависит от взаимной ориентации нормали
и напряженности. Если эти два вектора
образуют острый угол, поток положителен,
если тупой – отрицателен.
Поток
dFэ через
площадку, наклонную к силовой линии
(т.е. к вектору Е), равен также потоку
через проекцию этой площадки на
плоскость, перпендикулярную силовой
линии (см. рис. 1.1.2):
|
||||||||||||||||||||
|
30 |
|
|||||||||||||||||||
|
Теорема Гаусса для вектора напряженности электрического поля. Применение теоремы для расчета полей бесконечной плоскости, нити, сферы, равномерно заряженного по объему шара. Теорема Гаусса: Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, охваченной этой поверхностью, деленной на электрическую постоянную.
Применение теоремы для расчета полей: 1)Поле бесконечной плоскости:
2)Поле бесконечной нити:
3)Поле сферы: r<R: E=0 r>R: Внутри сферы R=0
4)Поле равномерно заряженного по объему шара: r<R: r>R:
|
||||||||||||||||||||
|
31 |
Потенциал-1)энергия, которой обладает единичный эл заряд, помещенный в электрическое поле. 2)работа по перемещению единичного точечного заряда в поле источника Q из точки 1 в точку 2(из данной точки на бесконечность) A=W1-W2=q(Фи1-Фи2) -убыль потенциальной энергии, ед заряд умноженный на разность потенциалов W-энергия заряда, помещенного в эл поле
Где, Q- источник поля, q-пробный заряд Потенциал(фи)=W/q [В]=Дж/кл
составляющая напряженности электрического поля по любому направлению равна градиенту потенциала в этом направлении, взятому с обратным знаком. Градиентом величины V называется ее производная по определенному направлению dV/dl. Если направление не указывается, то градиент соответствует направлению наиболее быстрого изменения V; это соответствует направлению вектора Е в данной точке, поскольку именно в таком направлении составляющая вектора Е совпадает с полной величиной напряженности поля:
Если расписать составляющие вектора Е по координатам х, у, z и в качестве l взять направления вдоль осей х у, z, то уравнение можно записать в виде:
Здесь dV/dx - частная производная V по направлению х при условии, что у и z фиксированы. В последнем примере напряженность электрического поля Е диполя в произвольной точке пространства. Складывая векторы напряженностей, создаваемых каждым зарядом в отдельности, получить этот результат было бы гораздо сложнее. Вообще говоря, для многих распределений зарядов гораздо проще рассчитать потенциал, а затем по формуле- напряженность электрического поля Е, чем вычислять по закону Кулона по отдельности Е для каждого заряда: скалярные величины складывать намного проще, чем векторы.
|
|||||||||||||||||||
|
Если
тело поставлено в такие условия, что
в каждой точке пространства оно
подвержено воздействию других тел с
силой, закономерно изменяющейся от
точки к точке, то говорят, что это тело
находится в поле сил. Центральное
поле сил потенциально. Убедимся, что
электрическое поле потенциально.
Вычислим работу, которая совершается
силами поля неподвижного точечного
заряда q над перемещающимся
в этом поле точечным зарядом Видно, что
работа не зависит от пути, по которому
перемещался в электрическом поле
заряд q', а зависит лишь от
начального и конечного положений
этого заряда (от r1 и r2)
Работа
сил электростатического поля при
перемещении заряда из одной точки
поля в другую не зависит от формы
траектории, а определяется только
положением начальной и конечной точек
и величиной заряда.
Следовательно, силы, действующие на
заряд q' в поле неподвижного
заряда q, являются консервативными,
а поле этих сил потенциальным.
Этот вывод легко распространяется
на поле любой системы неподвижных
зарядов, так как сила
|
||||||||||||||||||||
|
32 |
|
|||||||||||||||||||
|
|
||||||||||||||||||||
|
33 |
Вектор электрической индукции- векторная физическая величина, равная сумме вектора напряженности и вектора поляризации.
Можно
ввести вектор
электрической индукции
Теорема Гаусса: Для поля в диэлектрической среде электростатическая теорема Гаусса может быть записана еще и иначе (альтернативным образом) — через поток вектораэлектрического смещения (электрической индукции). При этом формулировка теоремы выглядит следующим образом: поток вектора электрического смещения через замкнутую поверхность пропорционален заключённому внутри этой поверхности свободному электрическому заряду:
В
дифференциальной форме:
|
|||||||||||||||||||
|
В
простейшем статич. случае Диэлектрич
проницаемость (наз. также статич. Дп.)
показывает, во сколько раз уменьшится
кулоновское взаимодействие зарядов,
не испытывающих обратного влияния
среды, при переносе их из вакуума в
данную среду. Одновременно Дп. |
||||||||||||||||||||
|
34 |
Проводник — вещество, в котором существуют свободные заряды, способные перемещаться под действием сколь угодно малого электрического поля. проводники имеют особые электрические заряды. Так, металлы, например, являются носителями таких зарядов, как электроны, которые потеряли связь с атомами. Их называют свободными электронами. Такие электроны в проводнике из металла, помещённом в электрополе, под воздействием сил этого поля будут передвигаться в направлении, которое будет противоположно напряжённости электрополя. Проводник называется уединенным, если он находится так далеко от других проводников и заряженных тел, что влиянием их электрических полей можно пренебречь. Потенциал уединенного проводника пропорционален его заряду.
Электроемкость
уединенного проводника -
физическая величина, измеряемая
отношением изменения заряда проводника
к изменению его потенциала: Электроемкость зависит от размеров и формы проводников, диэлектрической проницаемости среды, в которую они помещены, и расположения окружающих тел, но не зависит отматериала проводника. В СИ за единицу электрической емкости принимается фарада (Ф).
Электроемкость
уединенного проводящего шара
радиусом Rравна Конденсаторыпредставляют собой два проводника, разделенные слоем воздуха или диэлектрика, толщина которого малапо сравнению с размерами проводника. Проводники в этомслучае называют обкладками конденсатора.
Плоский
конденсаторсостоит
из двух одинаковых параллельных
пластин, находящихся на малом расстоянии
друг отдруга. Если заряды пластин
одинаковы по модулю и противоположныпо
знаку, то силовые линии электрического
поля начинаются на положительно
заряженной обкладке конденсатора и
оканчиваются на отрицательно
заряженной. Поэтому почтивсе
электрическое поле сосредоточено
внутри конденсатора.Если
пренебречь эффектами, возникающими
на краях обкладок плоского конденсатора
(краевой
эффект),
то электрическое поле плоского
конденсатора можно считать однородным.
Напряженность этого поля
Электроемкость
плоского конденсатора
Емкость
сферического конденсатора,
состоящего из двухконцентрических
обкладок сферической формы с
радиусами Емкость при параллельном и последовательном соединении конденсаторов.
Емкость
батареипараллельно
соединенных конденсаторовравна
сумме емкостей всех конденсаторов
При последовательном
соединении складываются
обратные величины их емкостей |
|||||||||||||||||||
|
Энергия заряженного уединенного проводника, конденсатора и системы точечных зарядов.
Сообщение
заряда проводнику связано с совершением
работы по преодолению сил кулоновского
отталкивания. Эта работа идет на
увеличение электрической энергии
проводника. Элементарная работа dA по
перенесению малого заряда dq из
бесконечности на уединенный проводник
равна
Аналогичное
выражение получается для конденсатора:
Для
системы точечных зарядов: |
||||||||||||||||||||
|
35 |
Выразим
энергию электрического поля между
обкладками конденсатора такой
формулой, чтобы в ней не было величин,
характеризующих сам конденсатор, и
остались бы только величины,
характеризующие поле. Понятно, что
этого можно достичь только одним
способом: вычислить энергию поля,
приходящуюся на единицу объёма. Так
как напряжение на конденсаторе U
= Ed,
а его ёмкость
Величина Sd представляет
собой объём V электрического
поля в конденсаторе. Поэтому плотность
энергии электрического
поля
|
|||||||||||||||||||
|
Рассчитаем энергию заряженного конденсатора, заряд которого q, напряжение на конденсаторе U, емкость С. В процессе разрядки конденсатора разность потенциалов между обкладками равномерно убывает от U до нуля, среднее же значение разности потенциалов равно
Тогда работа A, совершаемая электрическим полем при разряде конденсатора,
а энергия, которой обладает заряженный конденсатор, равна этой работе. Этой энергией обладает электростатическое поле конденсатора. Выразим ее через характеристики поля. Подставив в формулу
выражение
а также U = Ed, имеем
Энергия однородного поля пропорциональна объему, занимаемому полем. В связи с этим говорят об энергии единицы объема поля (объемной плотности энергии — We).
В СИ единицей объемной плотности энергии является джоуль на кубический метр (Дж/м3). Тогда
Полученная формула справедлива не только для однородного электростатического поля, но и для любого другого электростатического поля, а также и для переменного электрического поля. |
||||||||||||||||||||
|
36 |
Дифференциальная форма общего уравнения непрерывности такова:
где
Сигма(ро) - объемная плотность заряда В любой точке плотность заряда не меняется(постоянный ток)
Если q — сохраняющаяся величина, которая не может быть создана или уничтожена (например, энергия), тогда σ = 0, и уравнение непрерывности принимает вид:
|
|||||||||||||||||||
|
Закон Ома. Участок цепи, на котором не действуют сторонние силы, приводящие к возникновению ЭДС, называется однородным.
Закон Ома для однородного участка цепи был установлен экспериментально в 1826 г. Г. Омом. Согласно этому закону, сила тока I в однородном металлическом проводнике прямо пропорциональна напряжению U на концах этого проводника и обратно пропорциональна сопротивлению R этого проводника:
Закон Ома для полной цепи:
где:
Сопротивление Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:
где:
|
||||||||||||||||||||
|
37 |
Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними. Природа сторонних сил может быть различной. Например, в гальванических элементах они возникают за счет энергии химических реакций между электродами и электролитами; в генераторе — за счет механической энергии вращения ротора генератора и т. п. Сторонние силы совершают работу по перемещению электрических зарядов. Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда внутри источника, называется электродвижущей силой (э. д. с.),действующей в цепи: ξ=A/Q Эта работа производится за счет энергии, затрачиваемой в источнике тока, поэтому величину ξ можно также называть электродвижущей силой источника тока, включенного в цепь.
|
|||||||||||||||||||
|
При прохождении электрического тока в замкнутой цепи на свободные заряды действуют силы со стороны стационарного электрического поля и сторонние силы. При этом на отдельных участках этой цепи ток создается только стационарным электрическим полем. Такие участки цепи называются однородными. На некоторых участках этой цепи, кроме сил стационарного электрического поля, действуют и сторонние силы. Участок цепи, на котором действуют сторонние силы, называют неоднородным участком цепи. Рассмотрим
неоднородный участок цепи, участок,
содержащий источник ЭДС (т.е. участок,
где действуют неэлектрические
силы). Напряженность Напряжение
на концах участка цепи совпадает с
разностью потенциалов только в случае,
если на этом участке нет ЭДС, т.е. на
однородном участке цепи. Запишем обобщенный
закон Ома для участка цепи содержащей
источник ЭДС:
В
электротехнике часто используют
термин падение
напряжения –
изменение напряжения вследствие
переноса заряда через сопротивление
закон Ома для замкнутого участка цепи, содержащего источник ЭДС запишется в виде
|
||||||||||||||||||||
|
38 |
Правила Киргофа |
|||||||||||||||||||
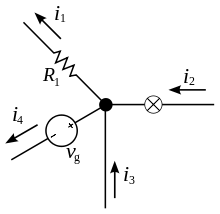
|
Определения Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют любой двухполюсник, входящий в цепь, например, на рис. отрезок, обозначенный U1, I1 есть ветвь. Узлом называют точку соединения трех и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый цикл из ветвей. Термин замкнутый цикл означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам. В терминах данных определений правила Кирхгофа формулируются следующим образом. Первое правило
Сколько тока втекает в узел, столько из него и вытекает. i2 + i3 = i1 + i4 Первое правило Кирхгофа гласит, что алгебраическая сумма токов сходящихся в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда. Второе правило Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:
для
постоянных напряжений
для
переменных напряжений Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля. Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, являетсязакон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее). Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.
|
||||||||||||||||||||
|
39 |
Электрическая мощность Р (Вт) определяется произведением напряжения на силу тока:
где U-напряжение на токоприемнике, В I-сила тока через токоприемник, А
Единица
мощности – 1 ватт 1вольт
Принимая
во внимание закон Ома (
В практике пользуются единицей мощности – киловатт (кВт), 1 Квт=1000 Вт.
|
|||||||||||||||||||
|
Мощность тепла, выделяемого в единице объёма среды при протекании постоянного электрического тока, пропорциональна произведению плотности электрического тока на величину напряженности электрического поля Математически может быть выражен в следующей форме:
где Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивления участка
В интегральной форме этот закон имеет вид
где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2. В случае постоянных силы тока и сопротивления:
Введем
плотность тепловой мощности Удельная мощность равна произведению вектора j на вектор Е - закон Дж-Л в диф форме |
||||||||||||||||||||

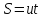 , ∆rx = vx ·
t при равномерном
, ∆rx = vx ·
t при равномерном при равноускоренном движениях
при равноускоренном движениях -при движении вниз
-при движении вниз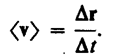
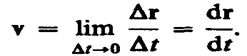
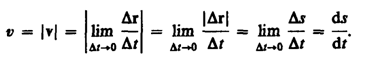
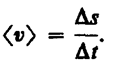
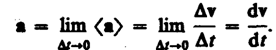
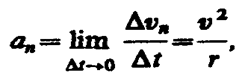
 и
сделав ряд преобразований:
и
сделав ряд преобразований:

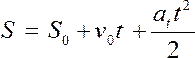 где v0 —
начальная скорость движения; Sо
— путь, пройденный до начала
отсчета; at — постоянное
касательное ускорение.
где v0 —
начальная скорость движения; Sо
— путь, пройденный до начала
отсчета; at — постоянное
касательное ускорение.


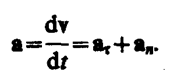
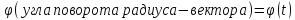 кинематическое уравнение вращательного
движения
кинематическое уравнение вращательного
движения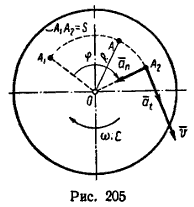
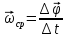

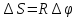 Делим обе части равенства на Δt
и переходим к пределу:
Делим обе части равенства на Δt
и переходим к пределу:
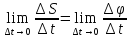 Отсюда имеем:
Отсюда имеем:
 ,
либо
,
либо
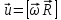
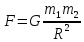 ,
где G = 6,67∙10–11 м3/кг∙с2 –
гравитационная
постоянная.
Закон
всемирного тяготения справедлив для
точечных, а также сферически симметричных
тел. Приближенно он выполняется для
любых тел, если расстояние между ними
значительно больше их размеров.
,
где G = 6,67∙10–11 м3/кг∙с2 –
гравитационная
постоянная.
Закон
всемирного тяготения справедлив для
точечных, а также сферически симметричных
тел. Приближенно он выполняется для
любых тел, если расстояние между ними
значительно больше их размеров.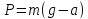 .
По третьему закону Ньютона
с той же по модулю силой опора или
подвес действует на тело; эта сила
называется реакцией опоры
.
По третьему закону Ньютона
с той же по модулю силой опора или
подвес действует на тело; эта сила
называется реакцией опоры 
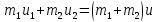
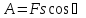 ,
,
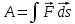 Работа равна нулю, когда тело движется
по инерции (F = 0), когда нет перемещения
(s = 0) или когда угол между перемещением
и силой равен 90° (cos а
= 0).
Единицей работы в СИ служит джоуль
(Дж).
Работа равна нулю, когда тело движется
по инерции (F = 0), когда нет перемещения
(s = 0) или когда угол между перемещением
и силой равен 90° (cos а
= 0).
Единицей работы в СИ служит джоуль
(Дж). ,
Кинетическая энергия
- энергия движения, ею обладают все
движущиеся тела.
,
Кинетическая энергия
- энергия движения, ею обладают все
движущиеся тела.
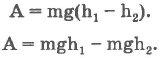 Величину mgh в соответствующей
точке, которая расположена на высоте
h, называют потенциальной энергией
тела, находящегося в поле тяжести.
Величину mgh в соответствующей
точке, которая расположена на высоте
h, называют потенциальной энергией
тела, находящегося в поле тяжести.
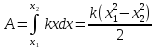 ,
, ,
,
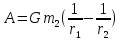
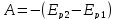

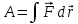 интегральная форма,
интегральная форма,
 дифференциальная форма.
дифференциальная форма. ,
импульсы
складываются векторно, а энергии
скалярно.
,
импульсы
складываются векторно, а энергии
скалярно.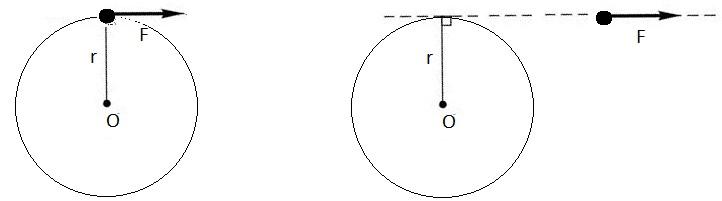

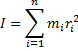
 или
или 


 .
. –
геометрическая сумма всех моментов
сил, то есть момент силы F,
сообщающий всем точкам тела
ускорение
–
геометрическая сумма всех моментов
сил, то есть момент силы F,
сообщающий всем точкам тела
ускорение  –
алгебраическая сумма моментов инерции
всех точек тела. Закон формулируется
так: “Момент силы, действующий на
вращающееся тело, равен произведению
момента инерции тела на угловое
ускорение”.
–
алгебраическая сумма моментов инерции
всех точек тела. Закон формулируется
так: “Момент силы, действующий на
вращающееся тело, равен произведению
момента инерции тела на угловое
ускорение”. ,
(1.11)
,
(1.11)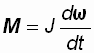 или
или 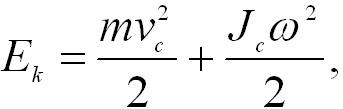 где vc –
скорость центра масс тела; Jc -
момент инерции тела относительно
оси, проходящей через его центр масс.
где vc –
скорость центра масс тела; Jc -
момент инерции тела относительно
оси, проходящей через его центр масс.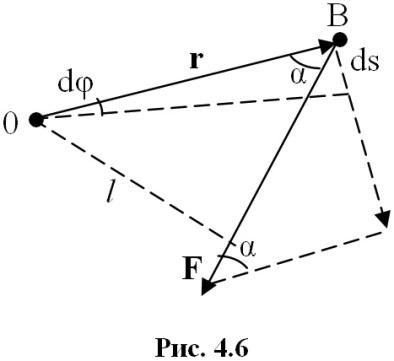 Работа при
вращении тела идет на увеличение его
кинетической энергии: dA = dEk
Работа при
вращении тела идет на увеличение его
кинетической энергии: dA = dEk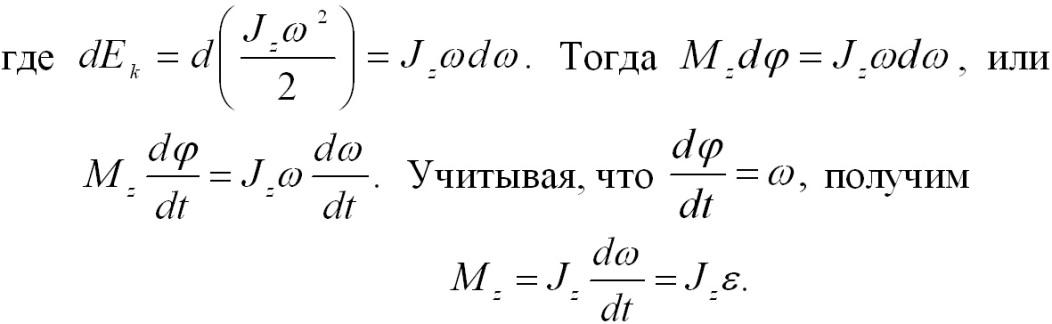

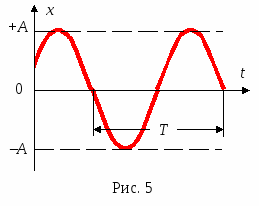

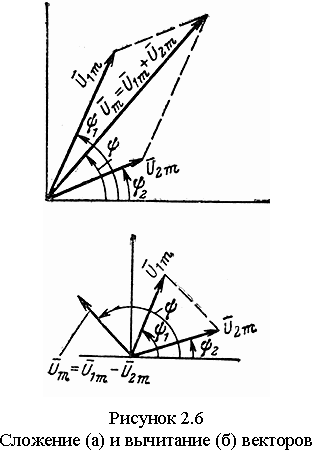
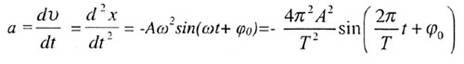
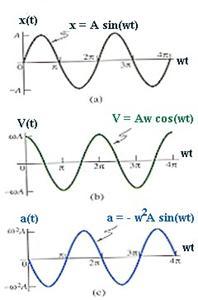
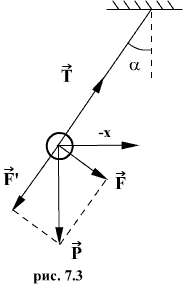
 ,
,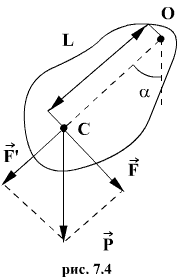
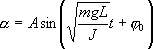
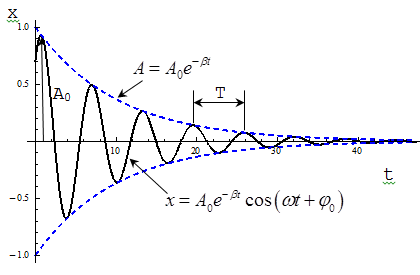
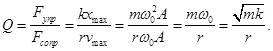
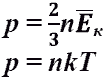 Вывод основного уравнения МКТ
Вывод основного уравнения МКТ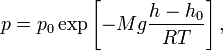 или
или
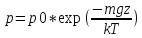
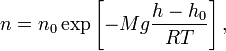
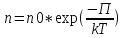 -
распределение
Больцмана( распред частиц в силовом
поле, где n-концентрация
частиц, П- потенциальная энергия,
n0-концетрация
частиц в точках поля, где П=0, k-постоянная
Больцмана, k=1,38*10^(-23),
Т- термодинамич температура )
-
распределение
Больцмана( распред частиц в силовом
поле, где n-концентрация
частиц, П- потенциальная энергия,
n0-концетрация
частиц в точках поля, где П=0, k-постоянная
Больцмана, k=1,38*10^(-23),
Т- термодинамич температура )
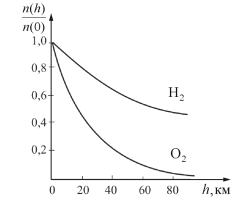
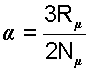
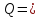 ∆U+
∆U+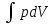
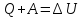
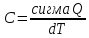


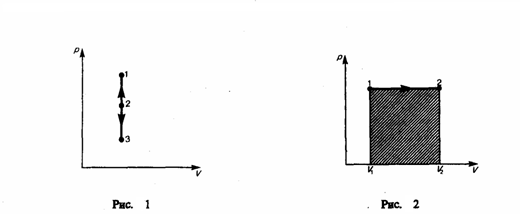
 =
=
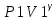 =
=
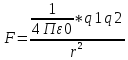


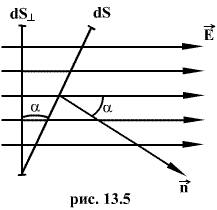
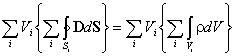 (1.7)
(1.7)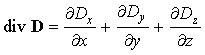

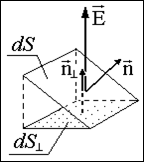
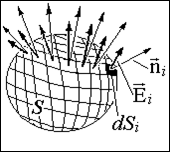 Рис.
1.1.3
Поток Fэ электрической
напряженности Е через замкнутую
поверхность S (рис. 1.3.3) определяется
как сумма элементарных потоков через
все площадки поверхности. В пределе,
когда количество площадок N стремится
к бесконечности, сумма потоков через
площадки переходит в поверхностный
интеграл от нормальной компоненты
напряженности En:
Рис.
1.1.3
Поток Fэ электрической
напряженности Е через замкнутую
поверхность S (рис. 1.3.3) определяется
как сумма элементарных потоков через
все площадки поверхности. В пределе,
когда количество площадок N стремится
к бесконечности, сумма потоков через
площадки переходит в поверхностный
интеграл от нормальной компоненты
напряженности En:
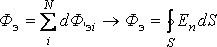 (1.1.3.)
К.
Гауссом в 1844 доказана теорема (теорема
Гаусса в интегральной форме),
устанавливающая связь источников
поля и потока напряженности через
произвольную поверхность, окружающую
источники.
(1.1.3.)
К.
Гауссом в 1844 доказана теорема (теорема
Гаусса в интегральной форме),
устанавливающая связь источников
поля и потока напряженности через
произвольную поверхность, окружающую
источники.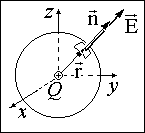 Для
доказательства выведем вспомогательную
формулу. Поток от точечного заряда
через произвольную окружающую его
сферу.
Для
доказательства выведем вспомогательную
формулу. Поток от точечного заряда
через произвольную окружающую его
сферу.
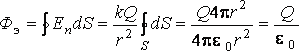 .
(1.1.4)
Силовые линии поля точечного
заряда перпендикулярны поверхности
концентрической сферы (см. рис 1.1.4). С
учетом этого факта формула (1.1.4)
выводится из выражения для поля
точечного заряда. Как видно, в этом
случае поток F э не
зависит от радиуса сферы, а зависит
только от Q .
.
(1.1.4)
Силовые линии поля точечного
заряда перпендикулярны поверхности
концентрической сферы (см. рис 1.1.4). С
учетом этого факта формула (1.1.4)
выводится из выражения для поля
точечного заряда. Как видно, в этом
случае поток F э не
зависит от радиуса сферы, а зависит
только от Q .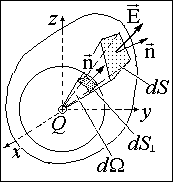 Рис.
1.1.5
Из (1.1.2) и (1.1.4) следует, что поток
поля точечного заряда через любую
поверхность, окружающую заряд, равен
потоку через сферу произвольного
радиуса, концентричную заряду.
Действительно, поток поля точечного
заряда через любую площадку dS,
вырезанную телесным углом dW из
произвольной поверхности, получается
таким же, как поток через площадку
Рис.
1.1.5
Из (1.1.2) и (1.1.4) следует, что поток
поля точечного заряда через любую
поверхность, окружающую заряд, равен
потоку через сферу произвольного
радиуса, концентричную заряду.
Действительно, поток поля точечного
заряда через любую площадку dS,
вырезанную телесным углом dW из
произвольной поверхности, получается
таким же, как поток через площадку 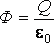 (1.1.5)
При
применении теоремы Гаусса для решения
задач, необходимо помнить, что в
уравнении (1.1.5) Q – сумма всех зарядов
внутри мысленной поверхности, через
которую вычисляется поток, в том числе
зарядов, принадлежащим атомам и
молекулам среды (так называемых
связанных зарядов).
(1.1.5)
При
применении теоремы Гаусса для решения
задач, необходимо помнить, что в
уравнении (1.1.5) Q – сумма всех зарядов
внутри мысленной поверхности, через
которую вычисляется поток, в том числе
зарядов, принадлежащим атомам и
молекулам среды (так называемых
связанных зарядов).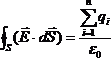
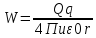
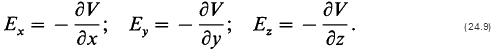
 сила,
действующая на точечный заряд,
находящийся в поле другого неподвижного
точечного заряда, является центральной.
Направление силы, действующей в любой
точке пространства на заряд, проходит
через центр заряда, создающего поле,
а значение силы зависит только от
расстояния до этого заряда
сила,
действующая на точечный заряд,
находящийся в поле другого неподвижного
точечного заряда, является центральной.
Направление силы, действующей в любой
точке пространства на заряд, проходит
через центр заряда, создающего поле,
а значение силы зависит только от
расстояния до этого заряда 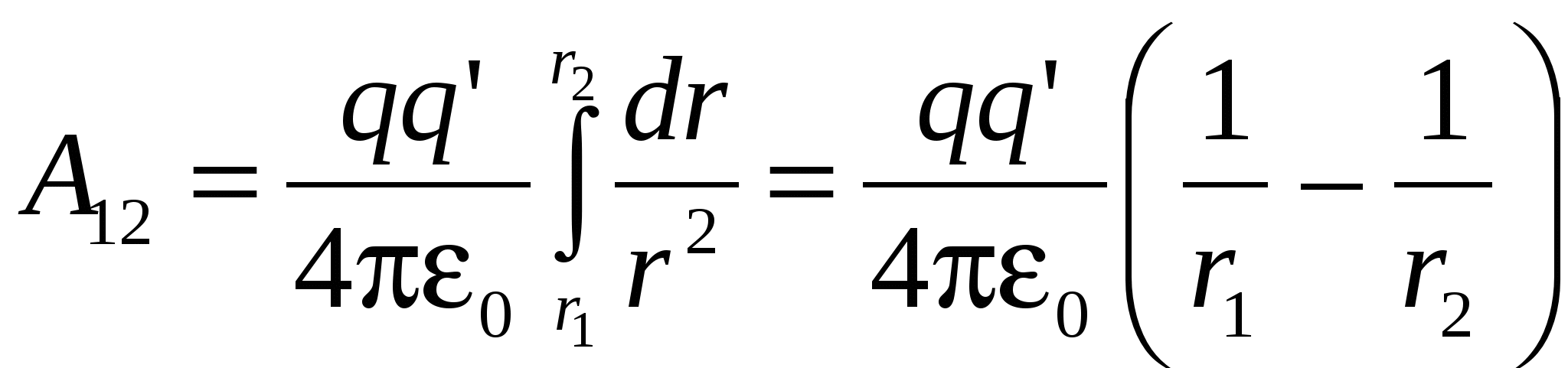 (1)
(1)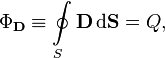
 .
Энергия проводника равна
.
Энергия проводника равна