Исходные данные к схеме № 15

№ варианта	a м	b м	P1 кН	P2 кН	P3 кН	P4 кН	q кН/м	Угол α	номера стержней
29	4	2	7	6	5	4	2	30о	1, 4, 6, 7
30	6	3	9	4	7	5	3	60о	3, 5, 8, 9

Пример выполнения расчетно-графической работы № 1

Схема конструкции

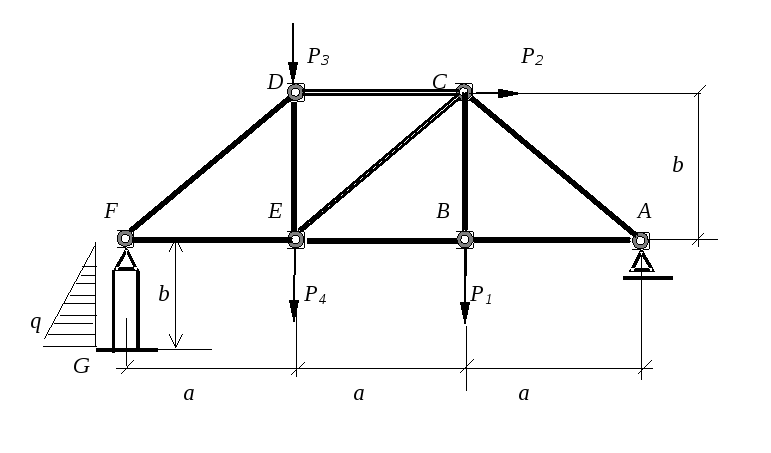Исходные данные: a = 4,0 м , b = 3,0 м, Р₁ = 1,0 кН, Р₂ = 2,0 кН, Р₃ = 3,0 кН, Р₄ = 4,0 кН, q = 1,0 кН/м

Для определения опорных реакций расчленяем конструкцию в шарнире F и рассматриваем две расчетные схемы:

а) расчетная схема и уравнения равновесия колонны

б) расчетная схема и уравнения равновесия фермы

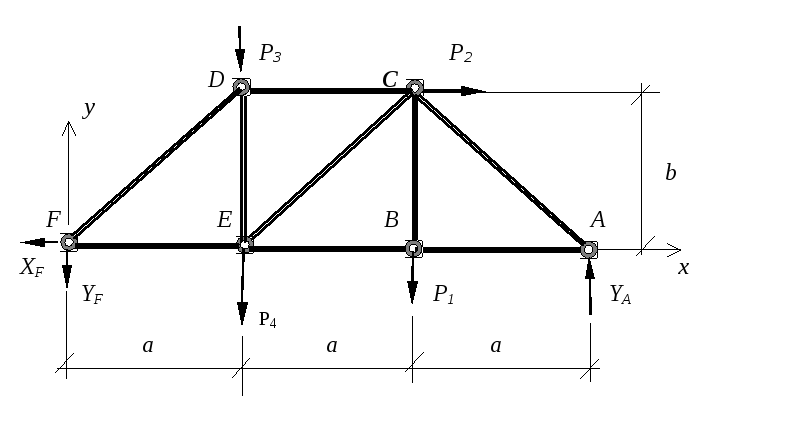4. Σ X = P₂ - X_F = 0,

5. Σ M_F = Y_A 3 a - P₁ 2 a - P₂ b - P₃ a - P₄ a = 0,

6. Σ M_A = Y_F 3 a + P₃ 2 a + P₄ 2 a + P₁ a - P₂ b = 0.

В результате совместного решения шести уравнений с учетом значений заданных величин получим:

Y_F = - 4,5 кН; Y_A = 3,5 кН; X_F = 2,0 кН;

X_G = - 8,0 кН; Y_G = 4,5 кН; M_G = 12,0 кНм.

Действительные направления реакций опор конструкции

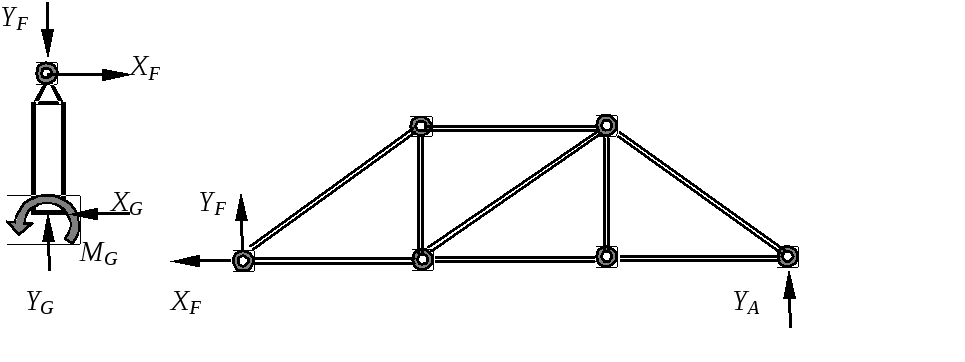
Определение усилий в стержнях методом вырезания узлов

Расчетная схема и уравнения равновесия узла А

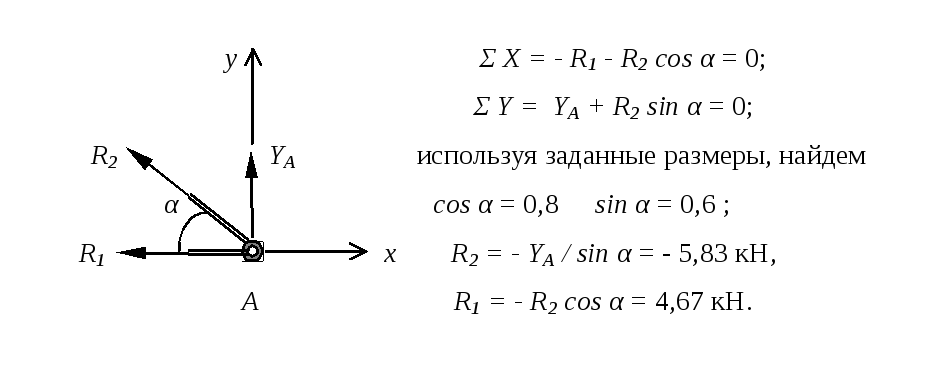
Расчетная схема и уравнения равновесия узла В

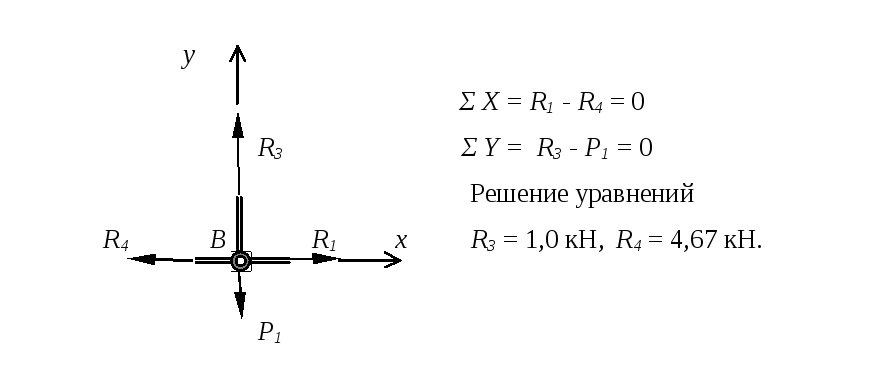
Расчетная схема и уравнения равновесия узла С

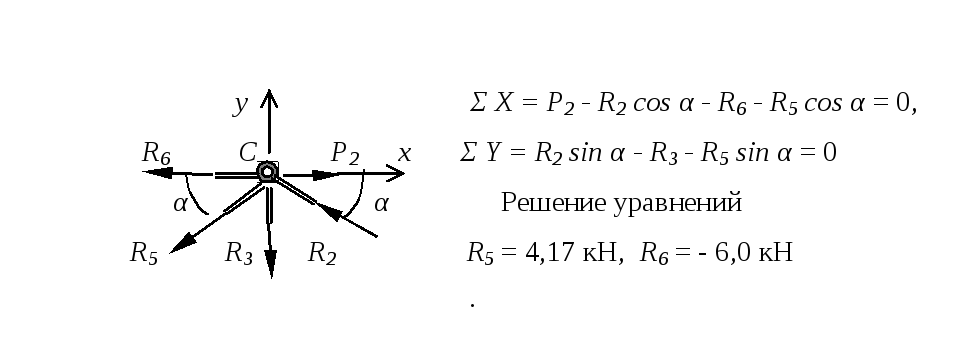
Расчетная схема и уравнения равновесия узла D

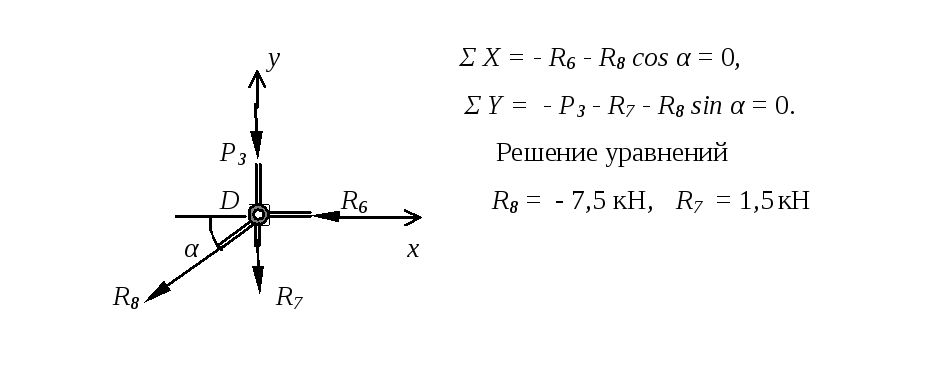
Расчетная схема и уравнения равновесия узла E

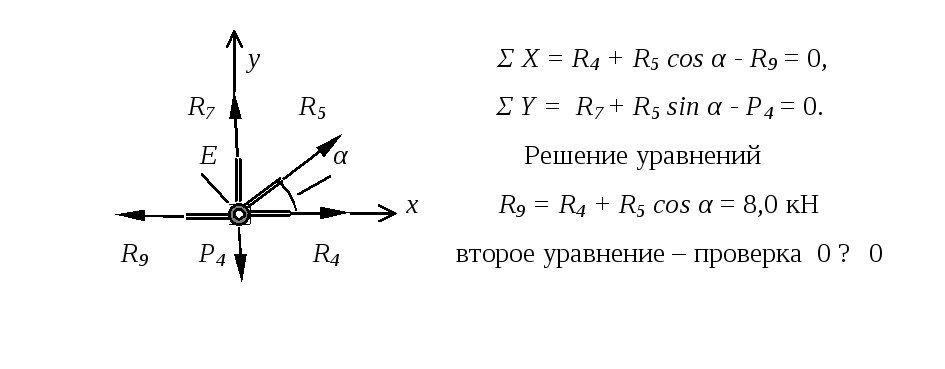
Проверка равновесия узла F

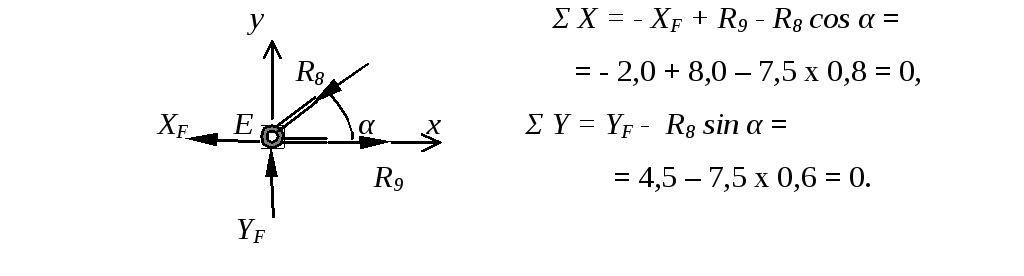
Определение усилий в стержнях методом сечений

При определении усилий этим методом следует действовать наиболее рационально, т.е. выбирать такие уравнения равновесия, в каждом из которых содержится только одно неизвестное усилие. Это достигается путем определения так называемых точек Риттера. Точка Риттера – это точка пересечения двух неизвестных усилий.

Сечение по стержням 2, 3 и 4

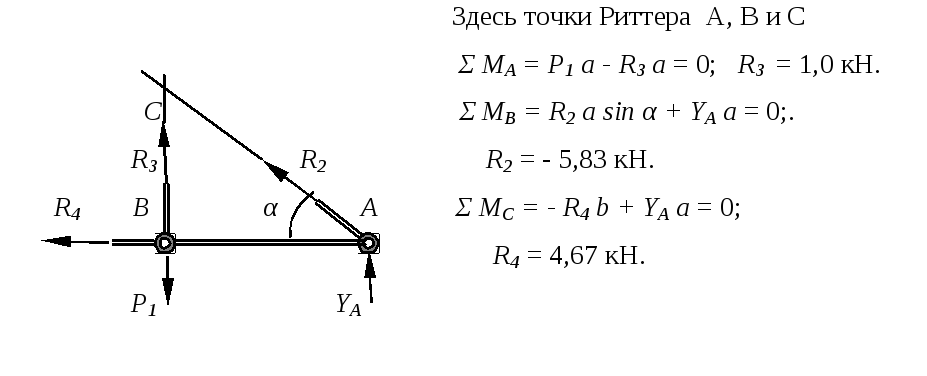
Сечение по стержням 4, 5 и 6

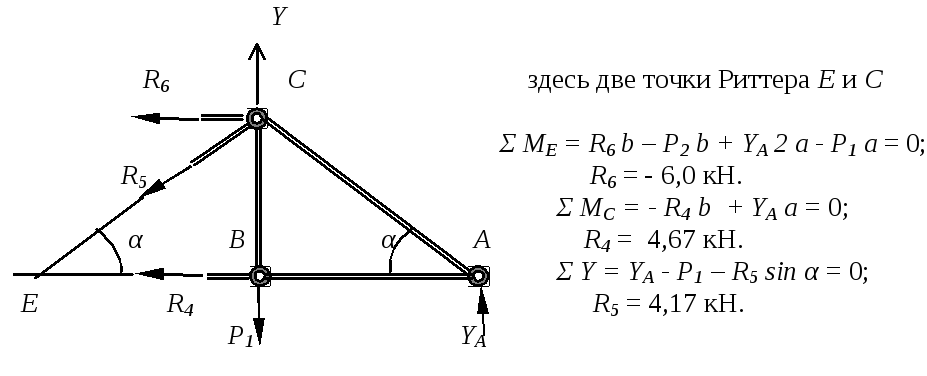
Сравнивая значения усилий, полученные двумя разными методами, убеждаемся в правильности выполненных вычислений.

Расчетно-графическая работа № 2

Работа представляет собой статический расчет стержневой пространственной конструкции, шарнирно закрепленной на монолитном фундаменте. Стержни связаны между собой также идеальными сферическими шарнирами.

Состав задания 1). Определить усилия во всех стержнях конструкции методом вырезания узлов (А, В и С) 2). Привести систему заданных сил (F₁, F₂ и F₃) к заданному центру О, расположенному на верхней поверхности фундамента и найти положение центральной оси системы заданных сил 3). Привести систему приложенных к фундаменту реакций стержней и убедиться в правильности решения задачи.

Схемы конструкций и варианты заданий

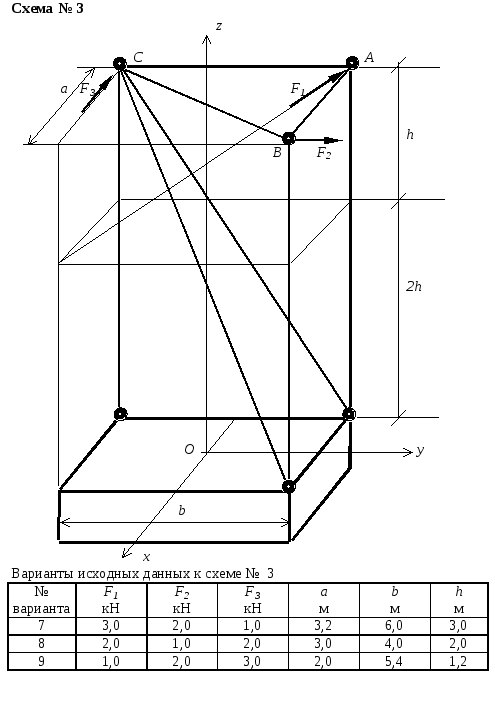
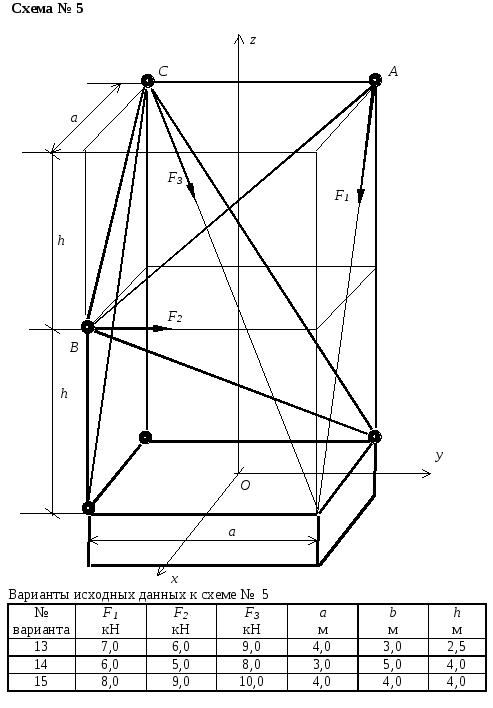
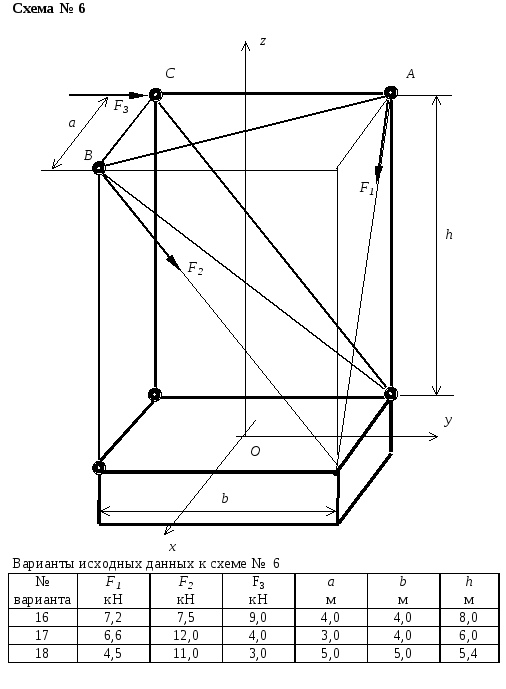
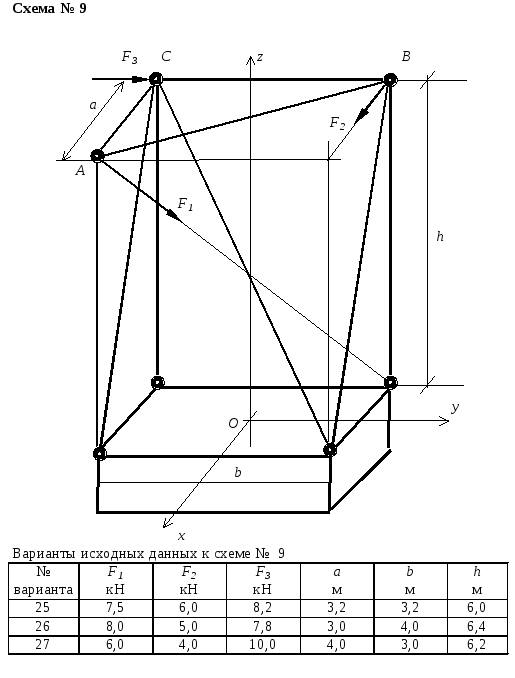
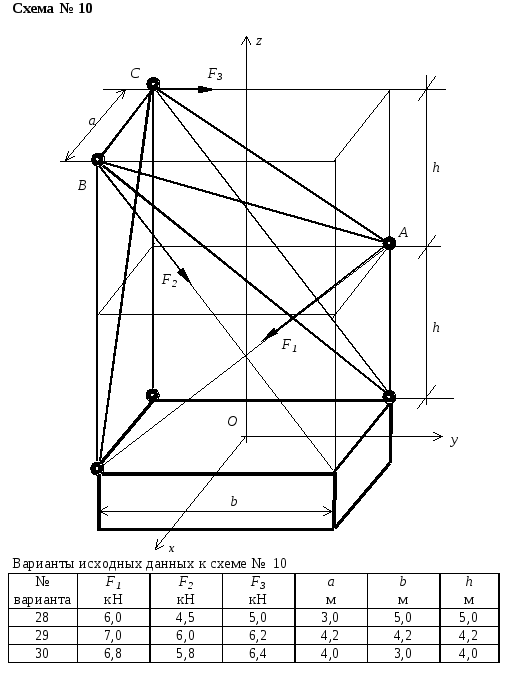
Пример выполнения расчетно-графической работы № 2

Работа представляет собой статический расчет пространственной стержневой конструкции, опирающейся на монолитный фундамент с помощью сферических шарниров. Определяются усилия во всех стержнях конструкции методом вырезания узлов. Кроме того, выясняется общее силовое воздействие на фундамент со стороны стержневой конструкции путем приведения системы сил к заданному центру О на верхней поверхности фундамента.

Расчетная схема узла А

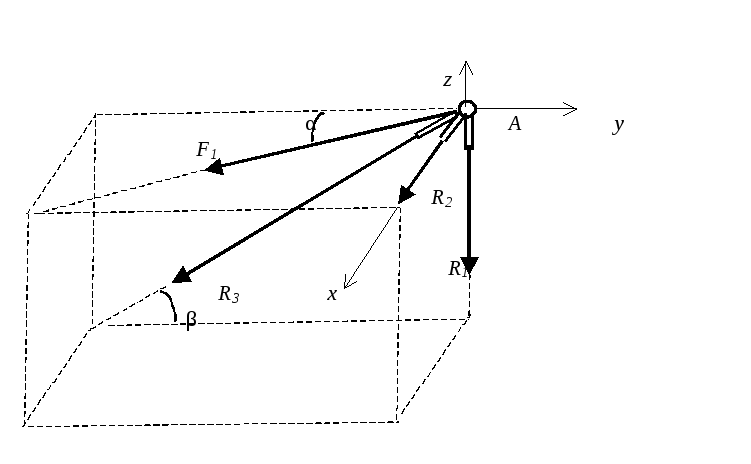
Уравнения равновесия:1. Σ X = F₁ sin α+ R₂ = 0; 2. Σ Y = - F₁ cos α - R₃ cos β = 0;

3. Σ Z = - R₁ - R₃ sin β = 0. При значениях функций

sin α = 0,6; cos α = 0,8; sin β= 0,447; cos β= 0,895 из уравнений

найдем R₂ = - 0,6 кН, R₃ = - 0,894 кН, R₁ = 0,4 кН.

Расчетная схема узла В

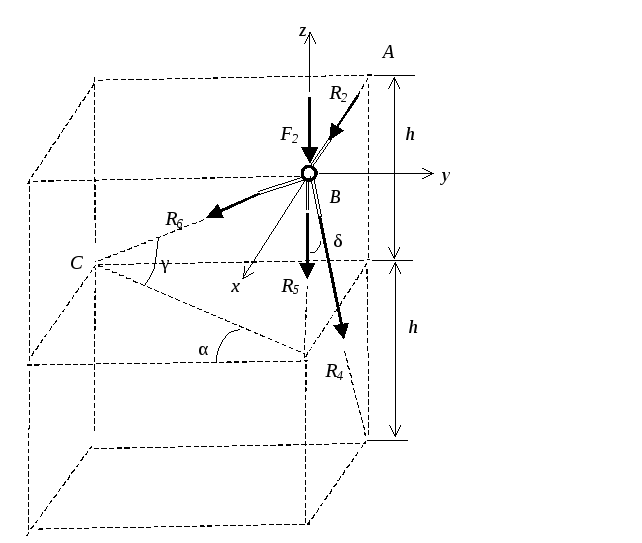
Уравнения равновесия

4. Σ X = R₂ - R₄ sin δ - R₆ cos γ sin α = 0;

5. Σ Y = - R₆ cos γ cos α = 0;

6. Σ Z = - F₂ - R₅ - R₄ cos δ - R₆ sin γ = 0.

Значения функций sin γ = 0,37 ; cos γ = 0,93 ; sin δ = 0,6; cos δ = 0,8.

Результаты решения уравнений R₆ = 0, R₄ = 1,0 кН, R₅ = - 2,8 кН

Расчетная схема узла С

Уравнения равновесия

7. Σ X = F₃ + R₉ cos φ = 0,

8. Σ Y = R₇ cos β - R₃ cos β = 0, 9. Σ Z = - R₈ - R₃ sin β - R₇ sin β - R₉ sin φ = 0. Вычислив значения функцийcos φ = 0,83; sin φ = 0,55;из уравнений равновесия найдем R₉ = - 3,6 кН; R₇ = 0,89 кН; R₈ = 1,2 кН.

Рассмотрим систему сил, действующих на фундамент со стороны стержней. При этом следует реакции растянутых стержней направлять «от узла», расположенного на фундаменте, а сжатых стержней «к узлу».

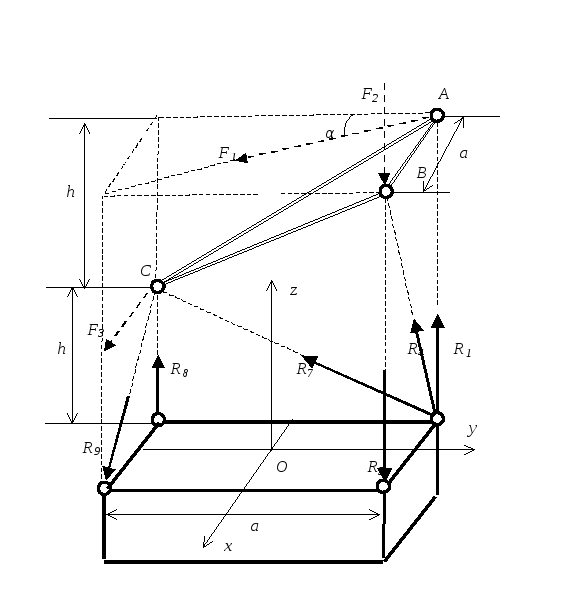
Приведем эту систему сил к заданному центру О на поверхности фундамента.Проекции главного вектора V на оси координат

V_x = Σ X = R₉ cos φ + R₄ sin δ = 3,6 кН; V_y = Σ Y = - R₇ cos β = - 0,8 кН;

V_z = Σ Z = R₁ + R₄ cos δ – R₅ + R₇ sin β + R₈ – R₉ sin φ = - 2,0 кН

Величина главного вектора V = = 4,2 кН

Проекции главного момента M_o

M_ox = Σ M_x = R₁ 0,5 b + R₄ cos δ 0,5 b – R₅ 0,5 b + R₇ sin β 0,5 b – R₈ 0,5 b + + R₉ sin φ = - 0,8 кНм

M_oy = Σ M_y = R₁ 0,5 a+ R₄ cos δ 0,5 + R₇ sin β 0,5 a + R₈ 0,5 a + R₉ sin φ 0,5 a + R₅ 0,5 a =11,4 кНм

M_oz = Σ M_z = - R₄ sin δ 0,5 b + R₇ cos β 0,5 a + R₉ cos φ 0,5 b = 6,0 кНм

Величина главного момента M_o = = 12,9 кНм

Для проверки выполненных расчетов найдем проекции главного вектора и главного момента для системы заданных сил F₁ , ,F₂ и F₃

V_x = Σ X = 3,6 кН; V_y = Σ Y = = - 0,8 кН; V_z = Σ Z = - 2,0 кН

M_ox = Σ M_x = F₁ cos α 2h – F₂ 0,5b = - 0,8 кНм

M_oy = Σ M_y = F₃ h + F₁ sin α 2h + F₂ 0,5 a = 11,4 кНм

M_oz = Σ M_z = F₃ 0,5b = 3,0 x 2,0 = 6,0 кНм

Результаты совпадают, следовательно, расчеты выполнены правильно.

Определим, к какому простейшему виду приводится система сил.

Так как V ≠ 0 и M_o ≠ 0, то система сил приводится либо к равнодействующей, либо к «динаме» - силовому винту.

Найдем скалярное произведение главного момента и главного вектора

M_o V cos (M_o^V) = M_x V_x + M_y V_y + M_z V_z = (-0,8) 3,6 + 11,4 (-0,8) + 6,0 (- 2,0) = - 24 ≠ 0.

Главный момент и главный вектор не перпендикулярны друг другу, следовательно система сил приводится к динаме.

Моментом динамы M_D называется проекция главного момента на линию действия главного вектора, поэтому M_D можно найти по формуле

M_D = (M_ox V_x + M_oy V_y + M_oz V_z) / V = -24 / 4,2 = -5,72 кНм

Знак минус означает, что вектор M_D направлен противоположно вектору V .

Расположение центральной оси системы определим, исходя из того, что векторы M_D и V расположены на этой оси и их одноименные проекции пропорциональны, т.е.

[M_x – (y V_z – z V_y)] / V_x = [M_y – (z V_x – x V_z)] / V_y =

= [M_z – (x V_y – y V_x)] / V_z = M_D / V ,

где x, y и z - координаты точек, расположенных на центральной оси.

Для определения координат x₁ и y₁ точки 1 пересечения центральной оси с плоскостью хОу выберем следующие два равенства

[M_x – (y₁ V_z – z₁ V_y)] / V_x = M_D / V, [M_y – (z₁ V_x – x₁ V_z )] / V_y = M_D / V , где положим z₁ = 0.

{ - 0,8 – [ y₁ ( - 2,0 ) – z₁ ( - 0,8 ) ] } / 3,6 = ( - 5,72) / 4,2 ; y₁ = - 2,05 м

{ 11,4 – [ z₁ 3,6 – x₁ ( - 2,0 ) ] } / ( - 0,8 ) = ( - 5,72) / 4,2 ; x₁ = 5,15 м

Аналогично определим координаты z₂ и x₂ точки 2 пересечения центральной оси с плоскостью xOz при y₂ = 0

[M_x – (y₂ V_z – z₂ V_y)] / V_x = M_D / V, [M_z – (x₂ V_y – y₂ V_x)] / V_y = M_D / V ,

{ - 0,8 – [ y₂ ( - 2,0 ) – z₂ ( - 0,8 ) ] } / 3,6 = ( - 5,72) / 4,2 ; z₂ = 5,12 м

{ 6,0 – [ x₂ ( - 0,8 ) – y₂ 3,6 ) ] } / ( - 2,0 ) = ( - 5,72) / 4,2 ; x₂ = - 4,1 м

Координаты z₃ и y₃ точки 3 пересечения центральной оси с плоскостью zОу ( x₃ = 0)

[M_y – (z₃ V_x – x₃ V_z)] / V_y = M_D / V , [M_z – (x₃ V_y – y₃ V_x)] / V_y = M_D / V

{ 11,4 – [ z₃ 3,6 – x₃ ( - 2,0 ) ] } / ( - 0,8 ) = ( - 5,72) / 4,2 ; z₃ = 2,86 м

{ 6,0 – [ x₃ ( - 0,8 ) – y₃ 3,6 ) ] } / ( - 2,0 ) = ( - 5,72) / 4,2 ; y₃ = - 0,91 м