10. Уравнения касательной к пространственной линии

Напомним, что прямая в пространстве, проходящая через точку , параллельно направляющему векторузадаетсяканоническими уравнениями:

(

рис. 11)

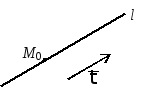
Рис. 11

Линия в пространстве может быть задана параметрическими уравнениями (рис. 12):

; ; ;.

Р

ис. 12

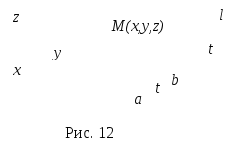
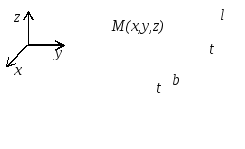
Будем предполагать функции дифференцируемыми (а значит, и непрерывными), а точку , где

,

обыкновенной; последнее означает, что производные координатных функций в этой точке не обращаются одновременно в нуль:

.

Пусть , и точкасоответствует значению параметра, так что

(рис. 13).

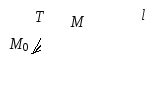
Рис. 13

Как и в случае плоской кривой, имеет место следующее Определение. Касательной к линии в точке называется предельное положение секущей при .

Это предельное положение определяется предельными значениями переменных величин, входящих в уравнения секущей . Последняя задается каноническими уравнениями:

.

Разделим знаменатели всех членов равенства на :

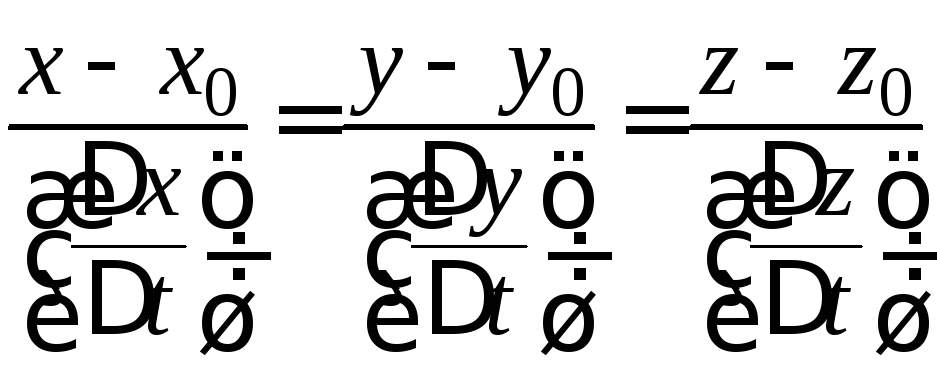. (23)

Поскольку

, ,,

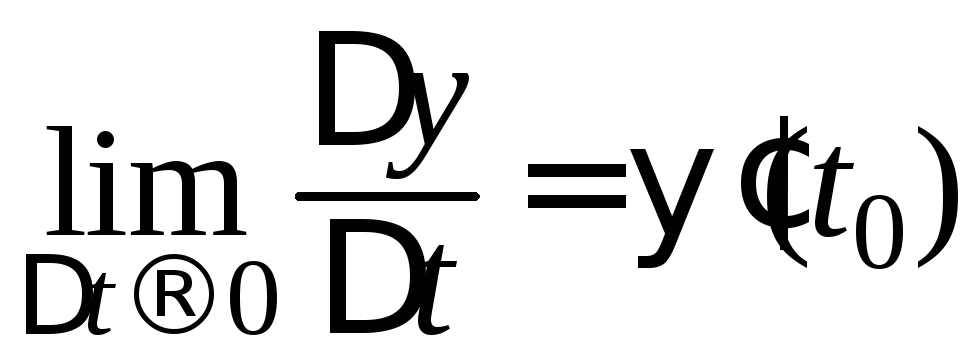то, переходя в (23) к пределу при ,получаем уравнения касательной :

,

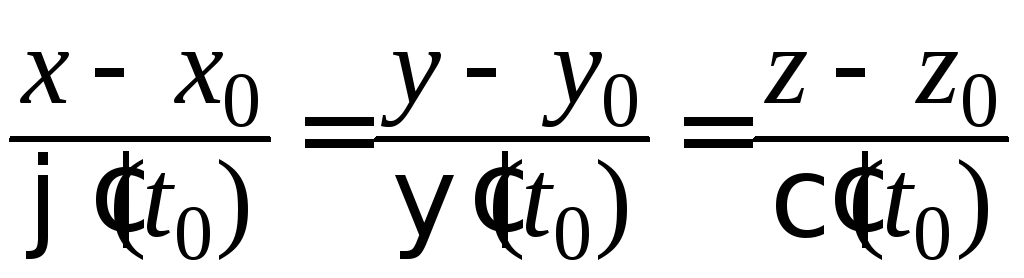или

.

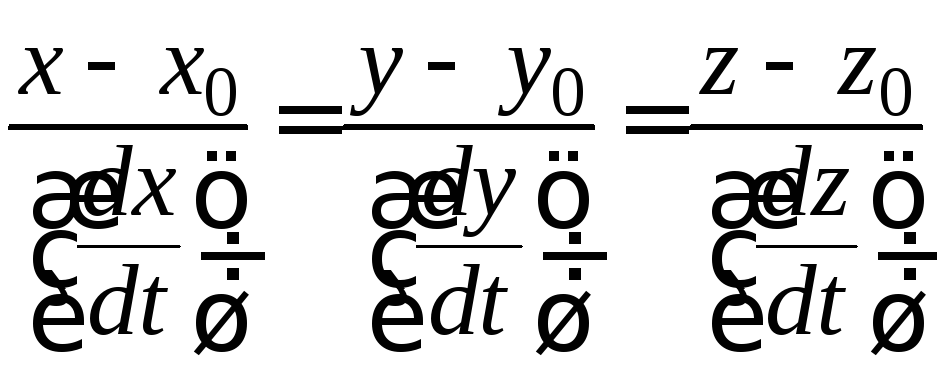Пример. Найдем канонические уравнения касательной к линии, заданной параметрическими уравнениями:

; ;

в точке , соответствующей значению параметра.

Находим производные:

; ;.

Полагая здесь , получаем канонические уравнения касательной в точке:

.

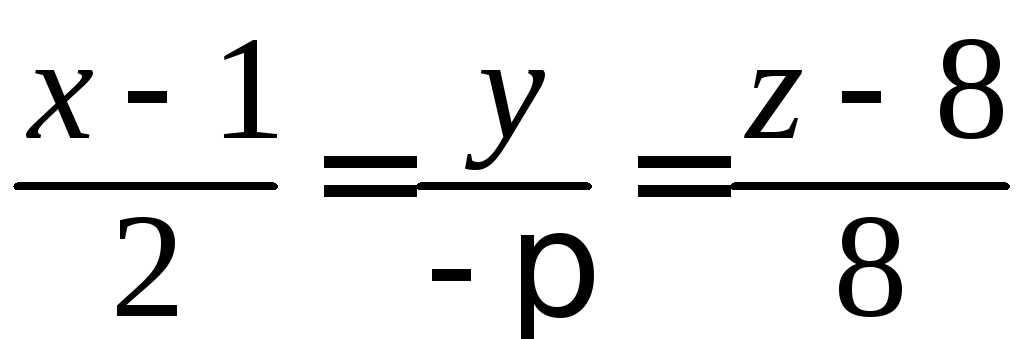11. Уравнение касательной плоскости и уравнения нормали к поверхности

Напомним, что плоскость , проходящая через точкуи перпендикулярная нормальному вектору(рис. 14), задается уравнением:

.

Напомним далее, что условие параллельности плоскости и пространственной прямой, заданной каноническими уравнениями

,

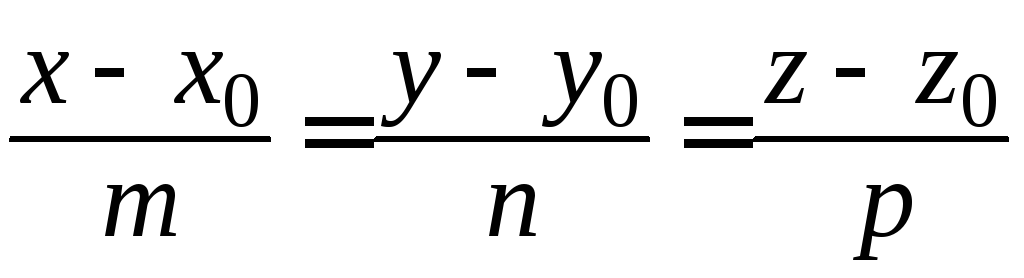имеет вид:

.

Определение. Прямая называетсякасательной прямой к поверхности в точке , если она является касательной в точкек какой-либо кривой, лежащей на поверхности(рис. 15).

Заметим что через точку можно провести разные кривыеи получить, соответственно, разные касательные прямыек поверхности(рис. 16).

Пусть поверхность задана уравнением.

Определение. Точка называетсяобыкновенной точкой поверхности , если выполняются три условия:

1. В окрестности точки существуют частные производные,,.

2. В точке частные производные непрерывны.

3. В точке частные производные не обращаются одновременно в нуль.

Теорема. Все касательные прямые к поверхности в неособенной точкележат в одной плоскости.

Доказательство. Пусть — плоскость, проходящая через точкуи имеющая нормальный вектор

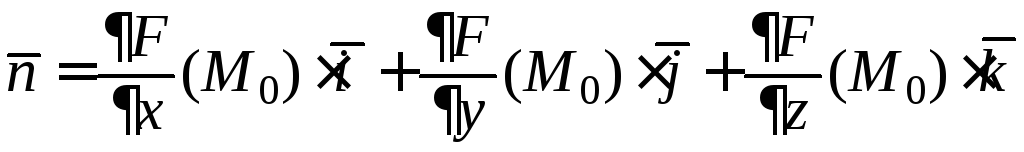
(вектор является ненулевым поскольку точкапо условию неособенная).Покажем, что в плоскости лежит любая касательная прямая. Пусть эта прямая является касательной к линии, имеющей параметрические уравнения

,

и

.

Канонические уравнения касательной к линии имеют вид:

.

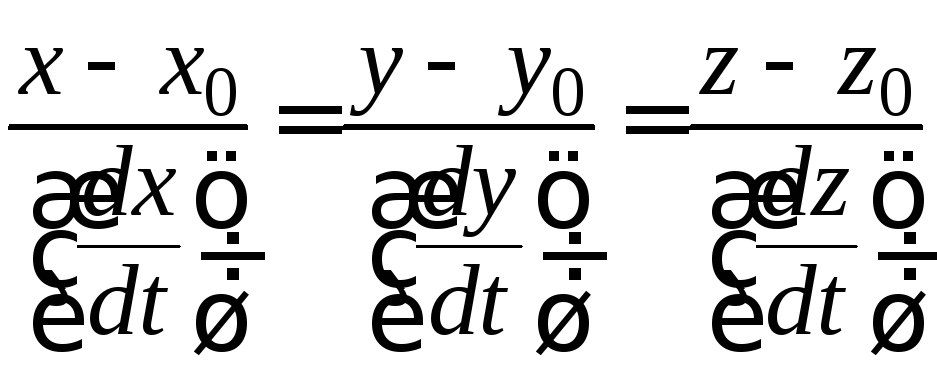Направляющий вектор касательной имеет координаты:

.

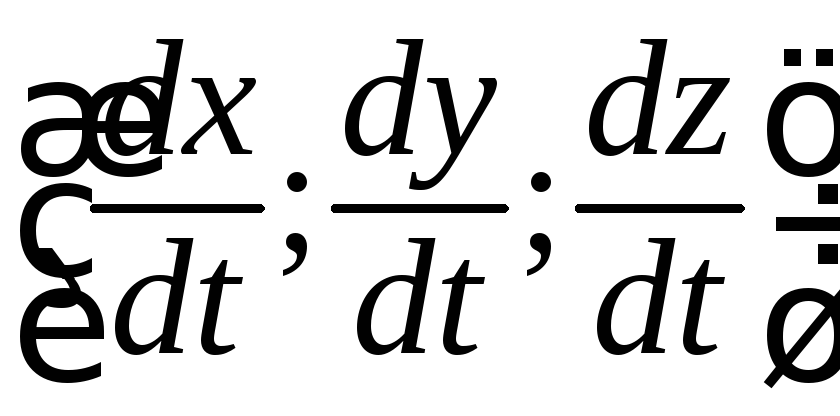Достаточно показать, что векторы иперпендикулярны; необходимым и достаточным условием для этого является равенство нулю скалярного произведения:. Имеем:

;

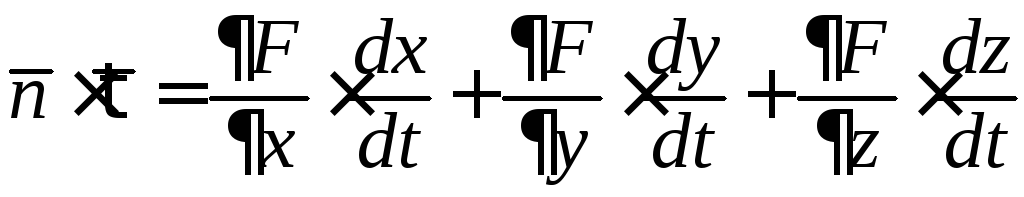правая часть здесь является полной производной сложной; при этом функцияпри всехтождественно равна нулю, поскольку точкалежит на поверхности, и, следовательно, ее координаты удовлетворяют уравнению). Итак,

. ▄

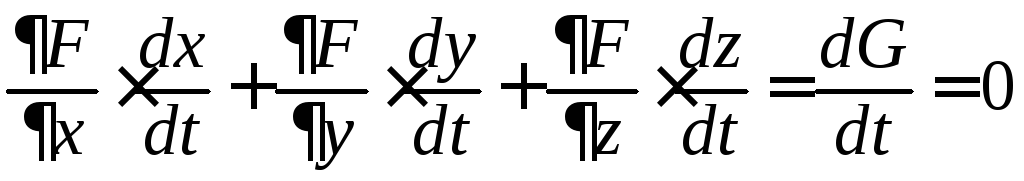Определение. Плоскость , в которой лежат все касательные прямые к поверхностив неособенной точке, называетсякасательной плоскостью к поверхности.

Пример. Найдем уравнение касательной плоскости к поверхности, заданной уравнением в точке. Здесь . Вычислим частные производные функции:

.

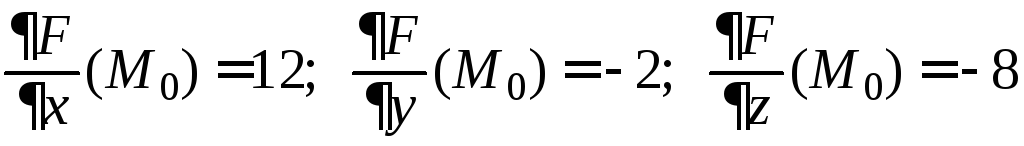Уравнение касательной плоскости:

.