III. Достаточное условие дифференцируемости

Теорема. Пусть функция удовлетворяет условиям предыдущей теоремы:

1. В окрестности точки она имеет частные производные .

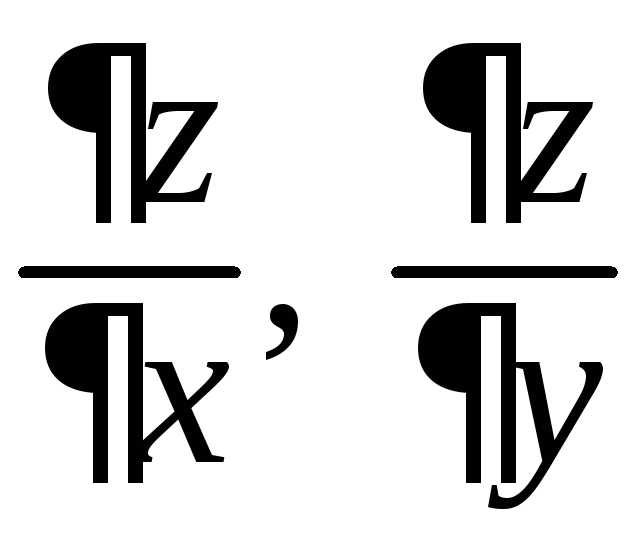2. В самой точке частные производные непрерывны.

Тогда дифференцируема в точке.

Доказательство. В силу условий теоремы справедлива формула (4) для полного приращения :

.

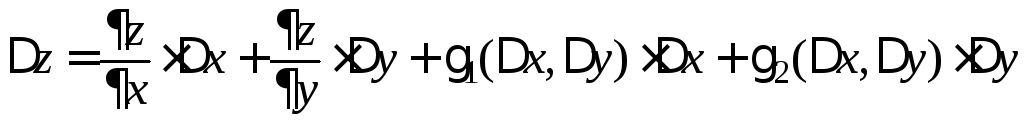Для того, чтобы придти к представлению (2), входящему в определение дифференцируемости, положим

.

Остается убедиться, что функция является бесконечно малой более высокого порядка, чем. Имеем

;

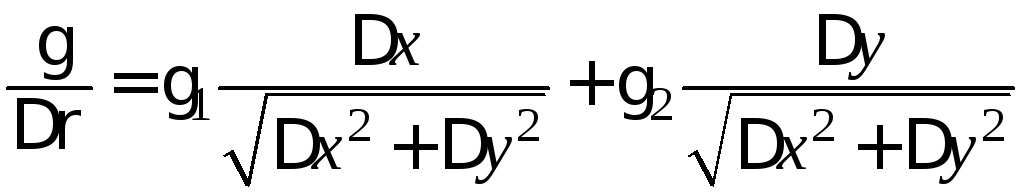при этом

и по свойствам бесконечно малых: при.▄

IV. Соотношение понятий непрерывности, дифференцируемости и частных производных

Как уже отмечено выше, из дифференцируемости функции нескольких переменных следует ее непрерывность. Здесь сохраняется логическая связь понятий, характерная для функций одной переменных. Однако из одного существования в точке частных производных еще не следуют ни дифференцируемость, ни даже непрерывность функции двух или более переменных. Далее, из непрерывности функции даже при условии существования частных производных не следует ее дифференцируемость. Дело здесь в том, что частные производные характеризуют в случае функции двух переменных ее поведение в малой окрестности точки не полностью, а только в направлениях координатных осей. Приведем соответствующие примеры.

Примеры. 1. Функция непрерывна в точке, но частные производные в этой точке не существуют.

Действительно, непрерывность функции обусловлена непрерывностью элементарных функций. В то же время разностное отношение

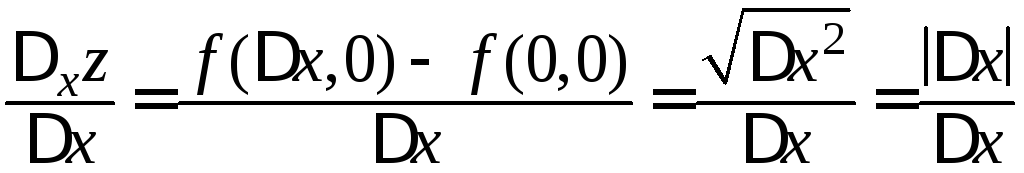
не имеет двустороннего предела при , поскольку прионо постоянно и равно, а припостоянно и равно.

2. Функция

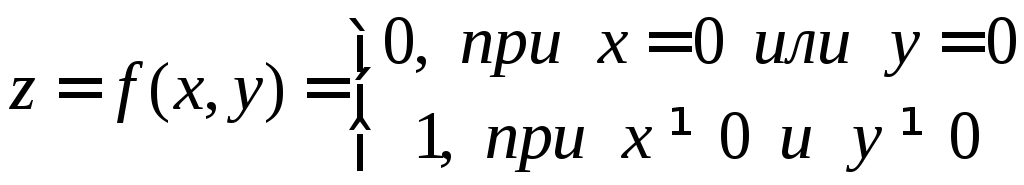
имеет в точке частные производные, но не является в этой точке непрерывной.

Действительно, полагая , имеем, откуда. Аналогично. В то же время предел функции в точкене существует, так как сколь угодно близко от нее существуют как значения, равные(в точках, не лежащих на координатных осях), так и значения, равные(в точках, лежащих на координатных осях).

3. Функция в точкенепрерывна, имеет частные производные, но не является дифференцируемой.

Действительно, непрерывность следует из того, что 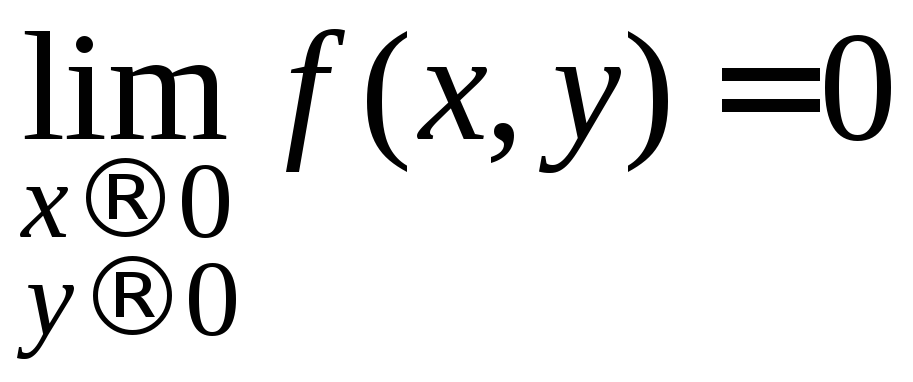, и. Далее,

,

.

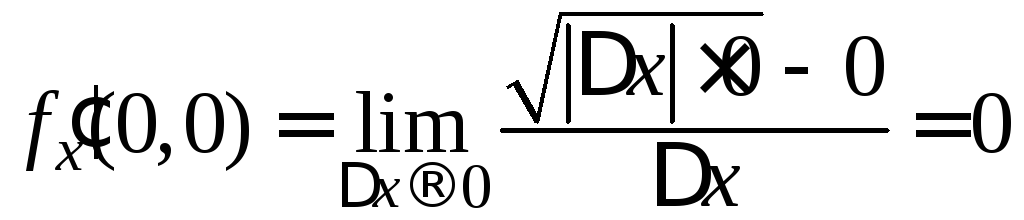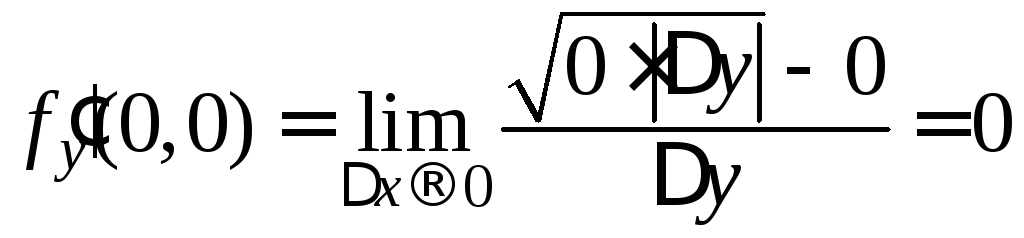В то же время при имеем. Как известно, эта функция не дифференцируема в точке. Если бы теперьбыла дифференцируема в точке, то присоответствующая функция — а это как раз— также была бы дифференцируема.

7. Частные производные сложной функции

Пусть в области задана функция двух переменных:

, (6)

у которой переменные ив свою очередь являются функциями переменныхи:

, (7)

заданными в области .

Тогда является сложной функцией независимых переменныхис промежуточными переменнымии:

. (8)

Рассмотрим задачу нахождения частных производных 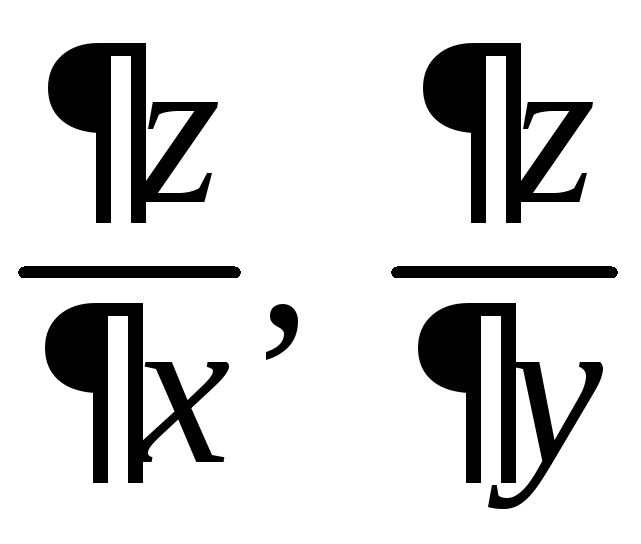этой сложной функции без использования явной записи (8).

Пусть точка , и функциии, согласно уравнениям (7), переводят ее в точку:

.

Теорема. Пусть выполняются три условия:

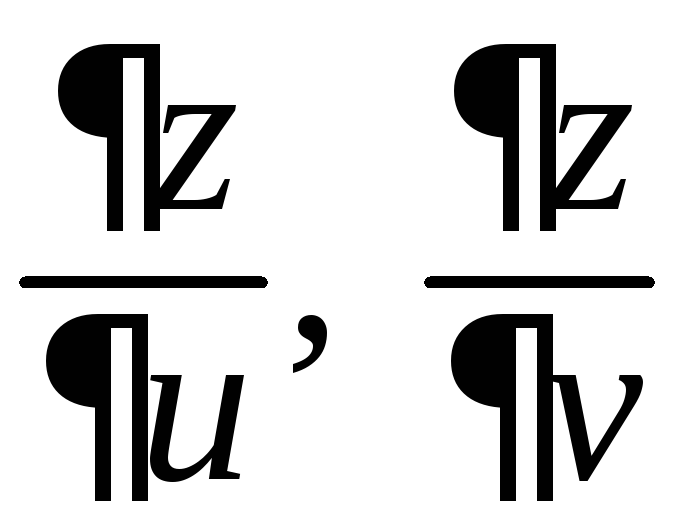1. В окрестности точки существуют частные производные, непрерывные в самой точке.

2. В точке существуют частные производные.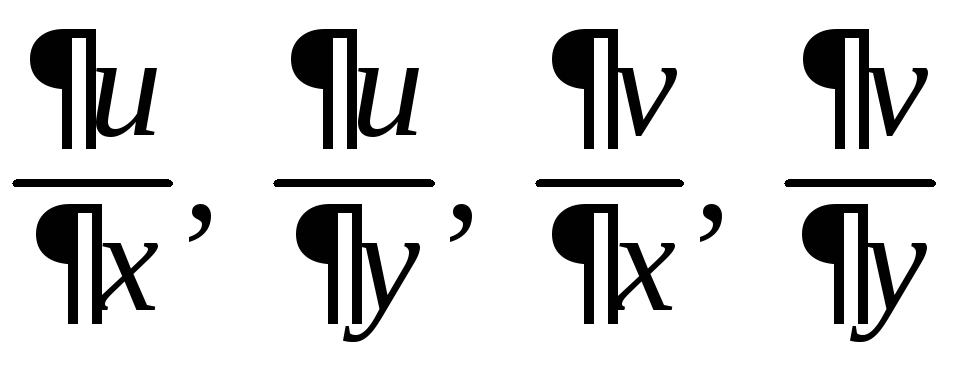

3. Функции непрерывны в точке.

Тогда в точке существуют частные производные сложной функции, и для них справедливы формулы:

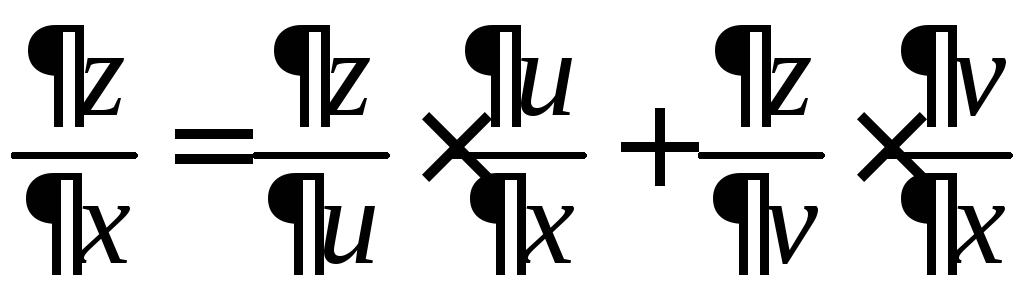
(9)

,

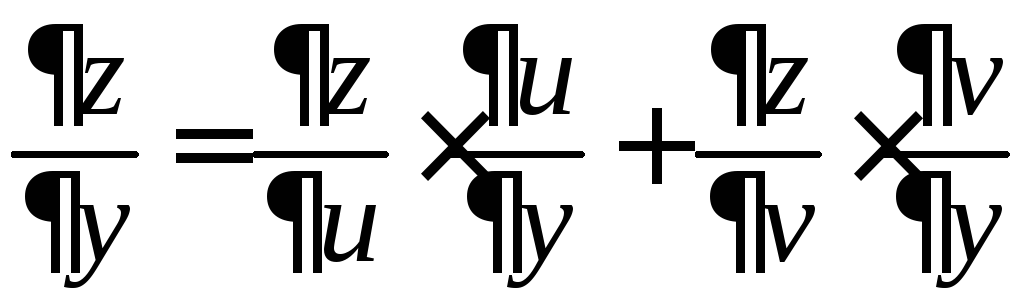или в другой записи:

.

Доказательство. Проведем его для частной производной . Придадим переменнойв точкеприращение; оно вызовет частные приращенияпромежуточных переменных, которые в свою очередь вызовут частное приращениесложной функции. В силу непрерывности частных производных (условие 1) к приращениюприменима формула (4):

,

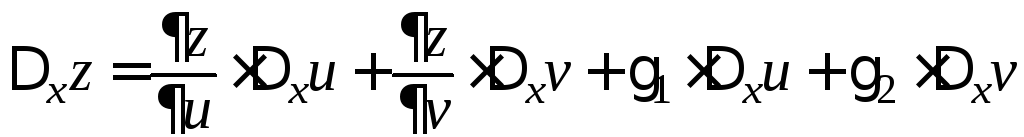откуда, деля на , получаем:

. (10)

Здесь 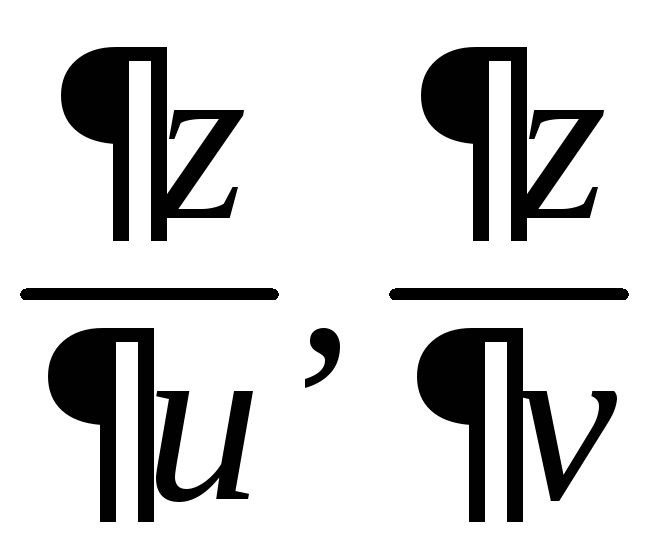— постоянные величины для фиксированной точки. Далее, в силу непрерывности функций(условие 3):

, ,

а тогда и величины в представлении (10) также стремятся к нулю.

Переходя в равенстве (10) к пределу при , получаем на основании свойств предела и условия 2:

,

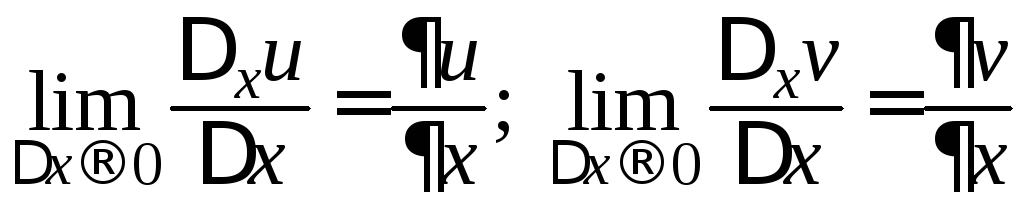и далее,

.

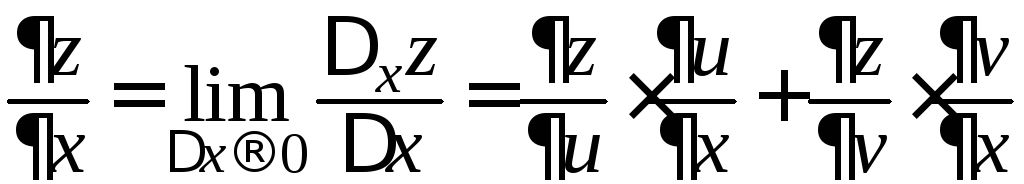Замечание. Аналогичные формулы имеют место для функций большего числа переменных. Например, в ситуации:

,

и

, ,,,

имеем:

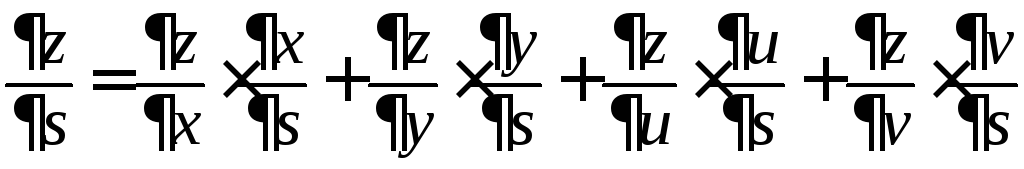
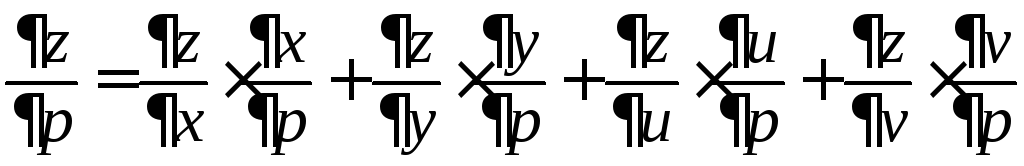
Пример. Пусть

;

.

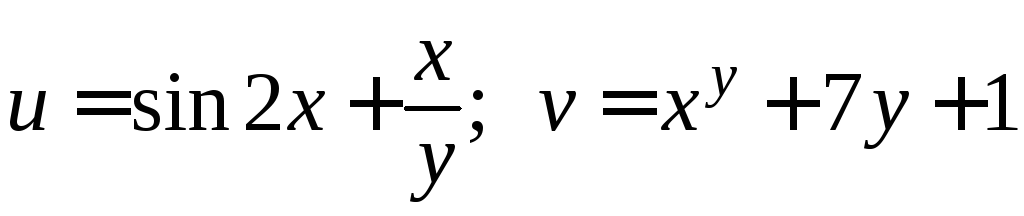Тогда

;

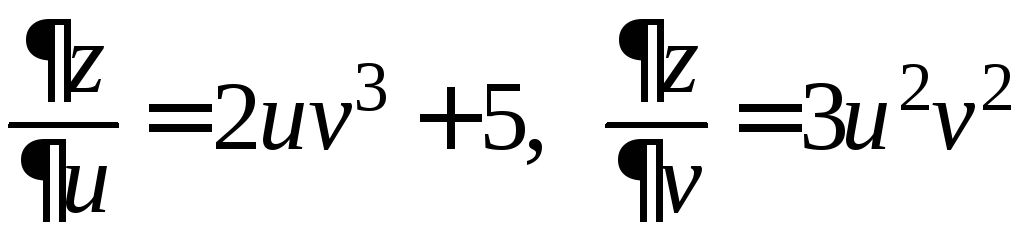далее,

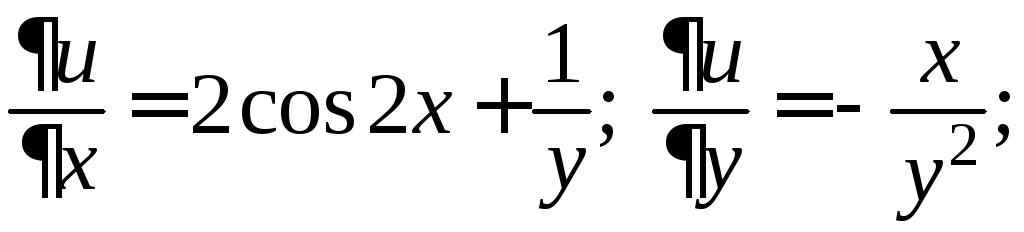
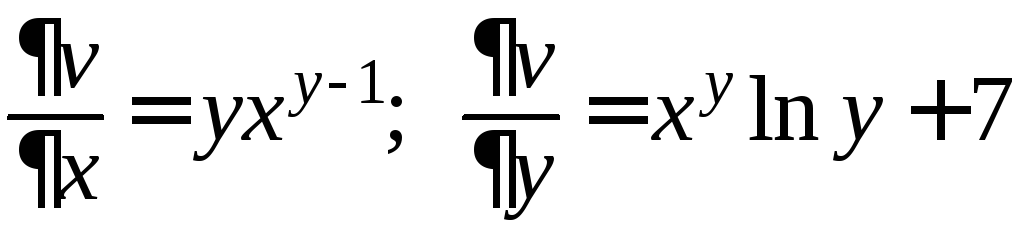
Поэтому

;

.
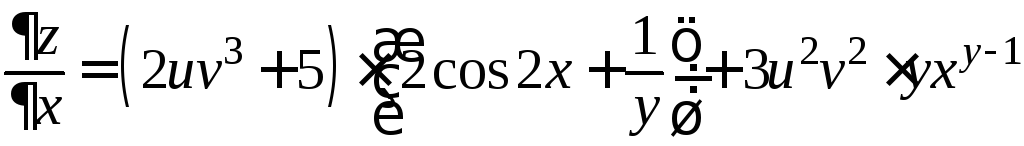
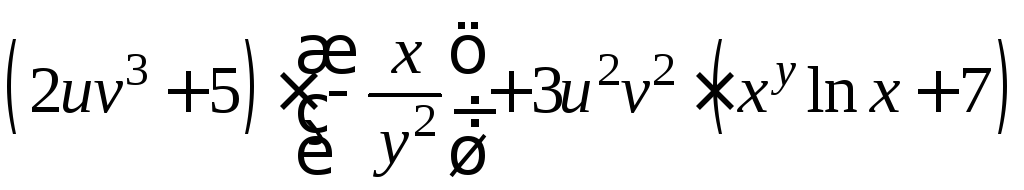