Кривые второго порядка (2 семестр)

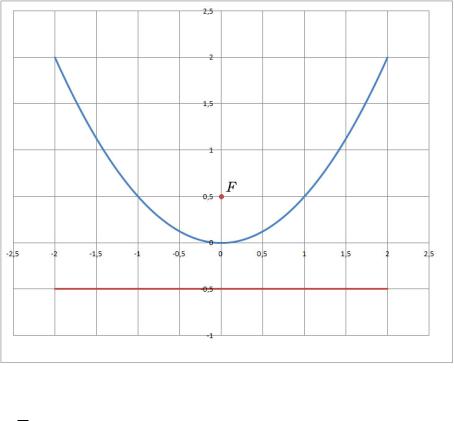
1Эллипс, гипербола и парабола на плоскости.

1.1Определения.

Определение 1. Параболой называется геометрическое место точек, равноудаленных от некоторой фиксированной точки ("фокуса" параболы) и некотрой фиксированной прямой ("директрисы" параболы)

Выведем каноническое уравнение параболы.

Введем систему координат. Фокус поместим в точку (0; p), директрисса

x2 = 4py каноническое уравнение параболы.

Показать, что график функции y = ax2 + bx + c парабола.

Для этого совершить параллельный перенос системы координат в точку ( 2ba ; c 4b2a (вершину параболы).

Определение 2. F1 è F2 фиксированные точки плоскости. 2a заданное расстояние.

Множество всех точек M, сумма растояний до который от точек F1 è F2 равно 2а, называется эллипсом.

1

F1 è F2 называются фокусами эллипса.

Вводим систему координат. Точку F1 помещаем в (0,с), точку F2 â (0,-ñ). Выводим каноническое уравнение эллипса.

Пусть точка M(x; y) произвольная точка эллипса. Заметим, что 2a > 2c (из неравенства треугольника для треугольника MF1F2). Записываем

2a длина большой оси эллипса, 2b малой. Фокусы лежат на большой

оси, внутри эллипса. Весь эллипс расположен в пределах прямоугольника fjxj < a; jyj < bg.

Как рисовать эллипс. Рисуем прямоугольник fjxj < a; jyj < bg и

вписываем в него кривую. Кривая касается прямоугольника в точках

(0; a) è ( b; 0).

Частный случай эллипса окружность (когда a = b = r, получаем уравнение x2 + y2 = r). В случае, если a = b получаем c = 0. Т.е. фокусы эллипса совпадают и являются центром окружности.

Определение 3. F1 è F2 фиксированные точки плоскости. 2a заданное расстояние.

Множество всех точек M, модуль разности растояний до который от точек F1 è F2 равен 2а, называется гиперболой.

F1 è F2 называются фокусами гиперболы.

Вводим систему координат так же, как в случае с эллипсом. Выводим уравнение гиперболы. Заметим, что в этом случае из неравенства

2

p

треугольника следует, что c > a. И новый параметр b = c2 a2. А вывод

уравнения практически идентичен.

xa22 yb22 = 1 каноническое уравнение гиперболы.

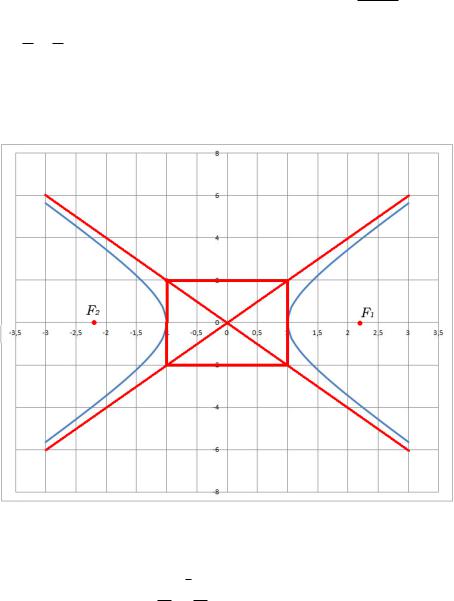
Как рисовать гиперболу. Рисуем прямоугольник fjxj < a; jyj < bg.

Теперь рисуем диагонали этого прямоугольника, но не только внутри прямоугольника, а целые прямые (это асимптоты гиперболы, их мы подробнее изучим позже). Гипербола касается прямоугольника снаружи в точках (0; a), а дальше уходит к нарисованым асимптотам.

Рассмотрим кривую, заданную уравнением y = 1=x. В школе ее

называли гиперболой, проверим, так ли это. Повернем систему координат на угол

4 . Тогда (вспоминаем формулы

эквивалентно тому, что x202 y202 = 1, а это каноническое уравнение гиперболы.

Здесь оси исходной системы координат это как раз асимптоты этой гиперболы.

1.2Классификация кривых второго порядка

Мы рассмотрели 3 кривые на плоскости, которые задаются уравнениями второго порядка. А какие вобще кривые на плоскости могут задаваться

3

Решая это уравнение находим подходящий угол , при повороте на

который системы координат, исчезает перекрестный член.

Можно и не разрешать уравнение для осуществления поворота. Применяя тригонометрические формулы и учитывая, что угол 2

qq

После поворота уравнение перешло к виду 1x02+ 2y02+a01x0+a02y0+a0 =

0

Первым делом предположим, что 1 2 6= 0.

Сделаем параллельный перенос так, чтобы исчезла линейная часть нашего уравнения. Для этого можно произвести замену переменной x0 =

x00 a01 y0 = y00 a02 .

2 1 2 2

Уравнение переходит к виду 1x002 + 2y002 + a000 = 0.

Предположим, что 1 2 < 0 (разных знаков) и a000 6= 0. Тогда уравнение становится каноническим уравнением гиперболы. Если a000 = 0, òî 1x002 =

y0 = y2. Если D < 0, уравенение не имеет решений (и значит, задает пустое множество точек плоскости). Если же D = 0, то получается одна прямая.

Таким образом, имеет место следующая теорема.

4

Теорема 1 (классификация КВП). Любая кривая второго порядка это одна из следующих кривых:

1.эллипс;

2.гипербола;

3.парабола;

4.пара прямых (пересекающихся, параллельных или совпадающих);

5.точка;

6.пустое множество.

Пример. Узнать, что за фигура задается уравнением x2 + xy + y2 + 2x + 2y + 1 = 0.

Решение. Нам нужно взять такой угол , что ctg 2 = 0. Поэтому

Ò.å. 3x002 + y002 = 23 , а это эллипс.

1.3Свойства КВП. Директриссы, эксцентриситет, симметрии.

Определение 5. Говорят, что фигура симметрична относительно точки O, если 8M 2 точка, симметричная M относительно точки O тоже принадлежит фигуре .

Точка O в этом случае центр симметрии фигуры .

Напомню, что точки M и M0 симметричны относительно точки O, åñëè O середина отрезка MM0.

Определение 6. Говорят, что фигура симметрична относительно прямой l, если 8M 2 точка, симметричная M относительно прямой l тоже принадлежит фигуре .

Прямая l в этом случае ось симметрии фигуры .

Óэллипса есть центр симметрии (в канонической системе координат это начало координат); 2 оси симметрии (в канонической системе координат это координатные оси).

Óокружности есть центр симметрии (центр окужности) и бесконечное множество осей симметрии (любая прямая, проходящая через центр окружности).

Óгиперболы есть центр симметрии (в канонической системе координат это начало координат), 2 оси симметрии (в канонической системе координат это координатные оси).

5

Óпараболы есть одна ось симметрии (в канонической системе координат это ось ординат); центров симметрии у параболы нет.

Óпары пересекающихся прямых есть 2 оси симметрии, если прямые не перпендикулярны (это биссектрисы образованных углов). И 4 оси симметрии у двух перпендикулярных прямых (2 биссектрисы и сами прямые). Центр симметрии точка пересечения прямых.

Óпары параллельных (или слипшихся) прямых бесконечно много центров симметрии (на прямой, лежащей посередине между этими прямыми). Оси симметрии это прямая, лежащая посередине между двумя исходными прямыми и все прямые, перпендикулярные им.

Определение 7. Пусть { некоторая кривая (не обязательно кривая

второго порядка), и существуют точка F и прямая l, а также число e, такие что для любой точки M 2 { выполнено равенство = e.

В этом случае прямая l называется дирректрисой кривой {, точка F фокусом, а число e называется эксцентриситетом кривой {.

Предложение 1. Очевидно, что у параболы есть дирректриса и эксцентриситет. Дирректриса прямая из определения параболы, а эксцентриситет равен 1.

Докажем, что дирректриса и эксцентриситет есть и у эллипса, и у гиперболы. Кроме вырожденного случая эллипса, окружности.

Дирректрисы эллипса.

самостоятельно.

Заметим, что эксцентриситет любого эллипса меньше единицы. (Для разных эллипсов он разный).

У эллипса, конечно, 2 симметричных дирректрисы (одна "работает" в паре с одним фокусом, другая в паре с другим).

Есть ли у эллипса другие дирректрисы? Заметим, что если l,

F дирректриса и фокус, то вся фигура должна быть симметрична относительно прямой l0 : l0 ? l; F 2 l0. Поэтому прямая l может быть только

параллельна одной из осей. Рассмотрим прямые x = x0 > 0, подходящие под условия. Таких всего одна. Рассмотрим прямые y = y0 > 0, таких нет совсем.

Эксцентриситет равен ac > 1. Других директрис у гиперболы нет. Доказательство аналогично.

Теорема 2. Пусть задана прямая l, точка F и число e < 1 (e > 1). Рассмотрим множество всех точек M (MFM;l) = e. Это множество точек образует кривую, которая является эллипсом (гиперболой).

6

получаем e2x2 = (x c)2+y2. Переносим в одну часть и получаем требуемое.

Определение 8. Асимптотой кривой { называется прямая, обладающая тем свойством, что расстояние от точки M 2 { до этой прямой стремится к нулю при неограниченном удалении точки M от начала координат.

Очевидно, что у эллипса ассимптот быть не может, потому что эллипс

не удаляется от начала координат.

Ассимптоты параболы: график параболы y = ax2 (каноническое

уравнение) возрастает быстрее любой прямой, поэтому ассимптот опять же

быть не может.

У гиперболы есть 2 ассимптоты: xa yb = 0. Доказательство с применением знанèé èç курса математического анализа. В первой четверти

1.4Касательные

Рассмотрим точки пересечения прямой и КВП.

КВП удовлетворяет уравнению: a11x2+2a12xy+a22y2+2a1x+2a2y+a0 =

0.

Прямая удовлетворяет уравнению: Ax + By + C = 0.

Выразим из второго уравнения одну из переменных, подставим в уравнение КВП, получим квадратное уравнение, у которого может быть 2 корня, у прямой и КВП две точки пересечения (если D > 0), нет точек

пересечения, (если D < 0) и две слипшиеся точки пересечения (если D = 0).

Определение 9. Прямая называется касательной к КВП, если точки их пересечения слипшиеся.

Бывает, что после подстановки в уравнение КВП, старший коэффициент зануляется и получается линейное уравнение, а следовательно, всего один корень. В этом случае кривая и прямая не называются касательными, хоть

и имеют всего одну точку пересечения. (Например, прямая, параллельная Oy пересекает параболу y = x2 в одной точке, но не касается ее).

Из условия D = 0 мы получаем уравнение касательной, которая касается КВП в точке (x0; y0)

(a11x0 + a12y0 + a1)x + (a12x0 + a22y0 + a2)y0 + (a1x0 + a2y0 + a0) = 0

Доказывать не будем.

Пример. Построить касательную к эллипсу 4x2 + y2 = 4, проходящую через точку (3; 2).

7

2Фокальные свойства эллипса, гиперболы и параболы.

Теорема 3 (Фокальное свойство эллипса) . Лучи света, исходящие из одного фокуса F1 эллипса, после зеркального отражения от эллипса проходят через второй фокус F2.

Теорема 4 (Фокальное свойство гиперболы) . Лучи света, исходящие из одного фокуса F1 гиперболы, после зеркального отражения от гиперболы кажутся исходящими из второго фокус F2.

Теорема 5 (Фокальное свойство параболы) . Лучи света, исходящие из фокуса параболы, после отражения от параболы образуют пучок, параллельный оси параболы.

относительно прямой l (получим точку F3).

Если указанные углы не равны, значит, прямая F2F3 пересекает прямую l не в точке M. А в другой точке M . Заметим, что F3M + F2M > F2F3. Значит, по другую сторону от точки M находится точка N такая, что

F3N + F2N = F3M + F2M. Действительно, пусть точка N бежит от точки M по направлению от M. Вначале сумма расстояний F3N + F2N

была меньше F3M + F2M, а на бесконечности станет больше. В силу непрерывности найдется искомая точка N. Точка N не совпадает с точкой M, так как они по разные стороны от точки M .

Вспомним определение эллписа. Эллипс это множество точек, сумма расстояний от которых до двух фокусов равна 2a. Таким образом F1M +

F2M = F3M + F2M = 2a = F3N + F2N = F1N + F2N. Поэтому точка N

тоже лежит на эллипсе, чего быть не может, так как эллипс и касательная пересекаются в одной точке.

Доказательство для гиперболы и параболы аналогично.

8

3Поверхности второго порядка.

3.1Краткий обзор. Определение основных ПВП.

Определение 10. Поверхностью второго порядка называется множество всех точек M(x; y), координаты которых удовлетворяют

уравнению a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz+2a1x+2a2y+2a3z+ a0 = 0; где квадратичная часть a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz

не равна нулю.

Часто будем писать F (x; y; z) = (x; y; z) + 2l(x; y; z) + a0 = 0, где(x; y; z) квадратичная часть уравнения ПВП; l(x; y; z) линейная часть уравнения ПВП; a0 свободный член.

3.1.1Распадающиеся плоскости

Иногда уравнение в правой части распадается в произведение двух линейных скобок (A1x + B1y + C1 + D1)(A2x + B2y + C2z + D2) = 0. Тогда, очевидно, в уравнение подходят все точки первой плоскости и все точки второй плоскости.

Если плоскости пересекаются, пускаем ось Оz по линии пересечения, координатные плоскости по биссекторам и получаем уравнение a2x2 b2y2 =

0.

Если прямые параллельны, пускаем коо плоскость Оуz по середине между ними и получаем уравнение x2 a2 = 0. В частном случае, когда

две плоскости совпадают, получаем уравнение x2 = 0.

Предложение 2. Если ПВП представляет собой пару плоскостей, то в некоторой ДСК его уравнение принимает вид a2x2 b2y2 = 0 (åñëè

плоскости пересекаются); x2 = a2 (если плоскости параллельны; а при a = 0 они слипаются).

9

3.1.2Циллиндрические поверхности

Определение 11. Циллиндрическая поверхность поверхность, которая в некоторой системе координат задается уравнением вида F (x; y; z) = F (x; y) = 0. (Т.е. уравнение в некоторой СК не зависит от

одной из переменных, а зависит только от двух оставшихся).

Заметим, что тогда на плоскости Оху уравнение F (x; y) = 0 задает кривую второго порядка. Поэтому можно найти такую ДСК, что F (x; y) = 0 и F (x; y) = 0 каноническое уравнение некоторой КВП. В зависимости

от того, какая это кривая, получается параболический циллиндр, эллиптический (круговой) циллиндр, гиперболический циллиндр и вырожденные виды циллиндров.

В частности, пара плоскостей, безусловно, является циллиндрической

поверхностью. Кроме того, вырожденными циллиндрическими поверхностями является прямая x2 + y2 = 0.

10