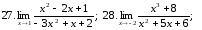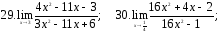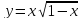- •Дифференциальное исчисление функции одной переменнойи нескольких переменных
- •Общие методические указания
- •Функция. Способы задания функции. Основные элементарные функции.
- •Предел и непрерывность функции.
- •Производная и дифференциал функции одной переменной.
- •Физические приложения производной.
- •Производная сложной функции.
- •Производные показательных и логарифмических функций.
- •Производные высших порядков
- •Производные неявной функции.
- •Касательная и нормаль к плоской кривой. Угол между двумя кривыми.
- •Дифференциал функции.
- •Исследование функций и построение их графиков
- •Индивидуальные задания. Задание1
- •Задание 2
- •Задание 3.
- •Задание 4.
- •Задание 5
- •Задание 8.
- •Задание 9.
- •Задание 10.
- •Задание 11.
- •2.Функции нескольких переменных.
- •Частные производные. Производная по направлению. Градиент.
- •Частные производные высших порядков.
- •Экстремум функции двух переменных
- •Условный экстремум
- •Расчетные задания.
Дифференциал функции.
Из
определений производной
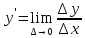 и предела переменной следует, что
и предела переменной следует, что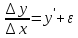 ,
или
,
или .
.
Главная
часть приращения функции, линейная
относительно приращения независимой
переменной, называется дифференциалом
функции и обозначается знаком
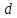 :
: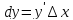 .
.
Дифференциал
независимой переменной
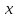 равен её приращению,
равен её приращению,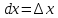 ,
поэтому
,
поэтому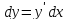 ,
т.е. дифференциал функции равен её
производной, умноженной на дифференциал
независимой переменной.
,
т.е. дифференциал функции равен её
производной, умноженной на дифференциал
независимой переменной.
Пример№13.
Найти полное приращение функции
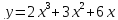 и её дифференциал, сравнить их значения
при
и её дифференциал, сравнить их значения
при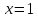 .
.
Решение: Полное приращение запишем в виде:
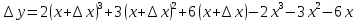
Преобразовав его, получим:
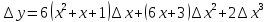
Найдём
полный дифференциал. По определению он
равен
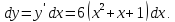 В
точке
В
точке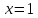 имеем
имеем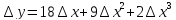 ,
,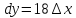 .
При достаточно малых
.
При достаточно малых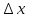 полное приращение функции и дифференциал
отличаются незначительно, т.е.
полное приращение функции и дифференциал
отличаются незначительно, т.е.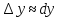 .
Это обстоятельство используется для
приближенных вычислений:
.
Это обстоятельство используется для
приближенных вычислений: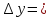
![]()
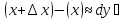
![]()
 ,
или
,
или![]()
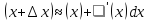 .
.
Пример№14:
Найти
приближенное значение
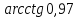 .
.
Решение:
Представим
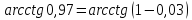 ,
тогда
,
тогда ,
,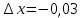 :
:
 .
.
Задания:1) Найти дифференциал функций:
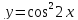 ;
;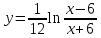 ;
; .
.
Вычислить приближенное значение:
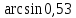 ; b).
; b).
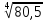 .
.
Определение
4.10.
Дифференциалом второго порядка называется
дифференциал
 ,
обозначается
,
обозначается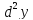 .
Тогда
.
Тогда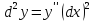 .
.
Исследование функций и построение их графиков
Схема исследования функции и построения графиков:
Определить область существования функции.
Исследовать функцию на четность и нечетность.
Найти координаты точек пересечения графика функции с осями координат.
Исследовать функцию на непрерывность, определить характер точек разрыва функции, если они имеются; найти асимптоты кривой.
Найти интервалы возрастания и убывания функции и её экстремумы.
Найти интервалы выпуклости вверх и вниз; определить точки перегиба.
Построить график функции.
Пример
№15
Построить график функции:
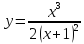 .
.
Решение:
Область существования функции
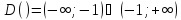
Функция не является ни четной ни нечетной.
Найдём точки пересечения с осями координат:
при
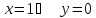
при
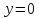 ,
,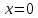 ,
т.е. кривая пересекает ось
,
т.е. кривая пересекает ось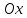 и осьO
и осьO в начале координат.
в начале координат.
Точка разрыва:
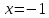 .
.
Исследуем характер разрыва:
 :
:
 ,
т.е. разрыв бесконечный 2-го рода.
,
т.е. разрыв бесконечный 2-го рода.
Найдём
асимптоты графика функции:
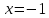 -
вертикальная асимптота; т.к.
-
вертикальная асимптота; т.к.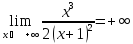 ,
,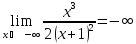 ,
горизонтальных асимптот нет.
,
горизонтальных асимптот нет.
Рассмотрим
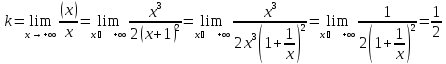
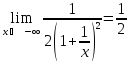

Таким
образом, график функции имеет наклонную
асимптоту
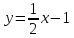 .
.
Вычислим первую производную и исследуем её знаки:
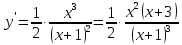
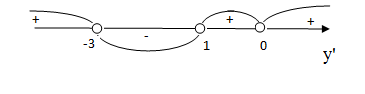
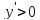 ,
для
,
для
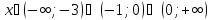 -
функция возрастает;
-
функция возрастает;
 ,
для
,
для
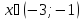 -
функция убывает.
-
функция убывает.
В
точках
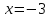 и
и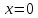 производная
производная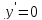 ,
но в окрестности точки
,
но в окрестности точки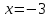 она меняет знак, поэтому в точке
она меняет знак, поэтому в точке функция имеет экстремум (максимум); в
окрестности точки
функция имеет экстремум (максимум); в
окрестности точки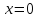 производная
производная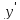 не изменяет знака, следовательно, точка
не изменяет знака, следовательно, точка не является точкой экстремума функции.
не является точкой экстремума функции.
Вычислим
значения:
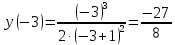 ,
, .
.
В
точке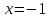 производная не существует, но в этой
точке не существует и сама функция,
поэтому
производная не существует, но в этой
точке не существует и сама функция,
поэтому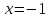 не является критической точкой для
производной.
не является критической точкой для
производной.
Вычислим вторую производную и исследуем её знаки:
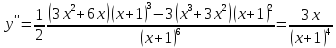
 для
для
 -
функция выпукла вверх.
-
функция выпукла вверх.
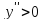 для
для
 -
функция выпукла вниз.
-
функция выпукла вниз.
В
точке
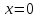 ,
,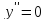 и в окрестности этой точки вторая
производная изменяет знак, значит, в
точки
и в окрестности этой точки вторая
производная изменяет знак, значит, в
точки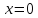 функция имеет точку перегиба.
функция имеет точку перегиба.
Результаты исследований наносим на график.
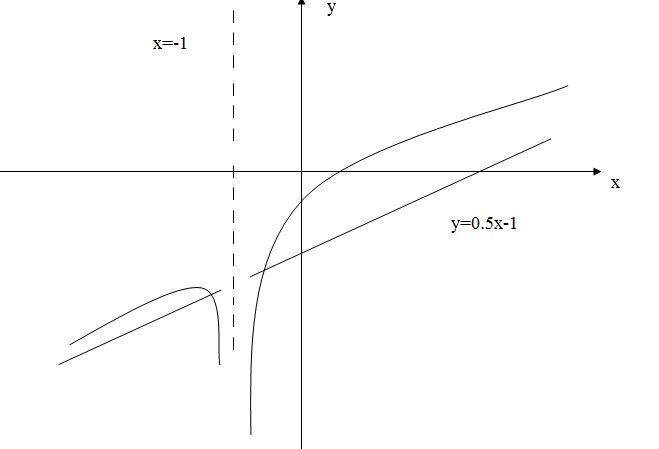
Задания: Построить графики функций:
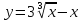 ;
;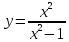 ;
;
Индивидуальные задания. Задание1
Вычислить предел:
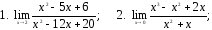
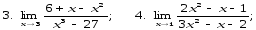
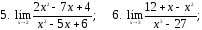
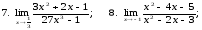
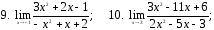
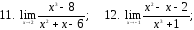



17.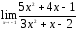 ;
18.
;
18.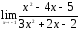 ;
;
19.
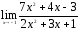 ;
20.
;
20.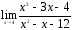 ;
;
21.
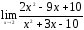 ;
22.
;
22.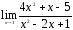 ;
;
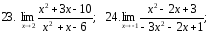
25. ;
26.
;
26.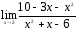 ;
;