7. Лінійні неоднорідні рівняння 2-го порядку

Лінійне неоднорідне рівняння із сталими коефіцієнтами має вигляд:

а₀у⁽ⁿ⁾ + a₁y^(n–1) + a₂y^(n–2) + ...+ a_ny=f(x)(4),

де а₀, а₁, а₂,..., a_nсталі, аf(x)– деяка неперервна функція (вона може бути сталою). Рівняння

а₀у⁽ⁿ⁾ + a₁y^(n–1) + a₂y^(n–2) + ...+ a_ny= 0(5)

у цьому випадку називається відповідним лінійним однорідним рівнянням.

Загальний розвязок рівняння (4) знаходять у вигляді:

У = у_одн + у_част. (6)

де у_одн= С₁у₁+ С₂у₂+...+ С_ny_n– загальний розвязок відповідного однорідного рівняння (5), ау_част.– деякий частинний розвязок рівняння (4).

Якщо права частина рівняння (4) має певний вигляд, то частинний розвязоку_част.можна знаходити не вдаючись до інтегрування.

Розглянемо ці випадки, користуючись таблицею:

Таблиця 2

Права частина диференціального рівняння	Корені характеристичного рівняння	Вигляд частинного розвязку
f(x) = Pm(x), де Pm(x) – многочлен степеняm.	a) Число 0 не є коренем характеристичного рівняння	Qm(x), де Qm(x)– многочлен степеня на вище m
	б) Число 0 є коренем характеристичного рівняння кратності l	xlQm(x)
f(x) = exm(x) де – дійсне число	а) Число не є коренем характеристичного рівняння	Qm(x)еx
	б) Число є коренем характеристичного рівняння кратностіl	Qm(x) еxxl
f(x) =m(x)cosx + + Qm(x)sin x, де m(x) i Qm(x) – многочлени степеня не вище mі хоч один з них має степіньm	а) Число і не є коренем характеристичного рівняння	Rm(x)cosx + Sm(x)sinx, де Rm(x) і Sm(x) – много-члени степеня не вищеm
	б) Число і є коренем характеристичного рівняння кратностіl	(Rm(x)cosx + +Sm(x)sinx) xl
f(x) = ex(m(x)cosx + + Qm(x)sinx)	а) Число + iне є коренем характерис-тичного рівняння	ex(Rm(x)cosx + +Sm(x)sin x)
	б) Число + i є коренем характерис-тичного рівняння кратності l	xlex(Rm(x)cosx + +Sm(x)sinx)

Зауваження 1. Якщо права частина рівняння (4) містить лише один доданок із синусом або з косинусом, то частинний розвязоку_част.все одно повинен містити обидва доданки.

Зауваження 2. Якщо права частина неоднорідного диференціального рівняння представляє суму двох функційf₁(x)іf₂(x)спеціального вигляду, то частинний розвязоку_част.шукають у вигляді

у_част.= (у₁)_част.+ (у₂)_част.,

де у_{1 част.}– частинний розвязок, що відповідає функціїf₁(x), ау_2част.– частинний розвязок, що відповідаєf₂(x).

П р и к л а д 13. Розвязати рівняння:

у +у = 12х².

Р о з в я з о к. Знаходимо загальний розвязок у_однвідповідно однорідного рівняння.

Характеристичне рівняння має вигляд:

k³ + k² = 0, його корені k₁= – 1,k₂=k₃= 0,

отже,

у_одн= С₁+ С₂х+ С₃е^–х

Визначимо вигляд частинного розвязкуу_част.^. Так як 0 – двократний корінь характеристичного рівнянняl= 2 і враховуючи, що права частина диференціального рівняння є многочлен другого степеня, то частинний розвязоку_част.будемо шукати у такому вигляді:

у_част. = (Ах²+ Вх+ С)х²= Ах⁴+ Вх³+ Сх².

Для знаходження невизначених коефіцієнтів А, В, С шукаємо похідні:

у_част. = 4Ах³+ 3Вх²+ 2Сх,

у_част. = 12Ах²+ 6Вх + 2С,

у_част. = 24Ах+ 6В

і підставляємо знайдені похідні в дане диференціальне рівняння:

24Ах + 6В + 12Ах²+ 6Вх + 2С12 х²

П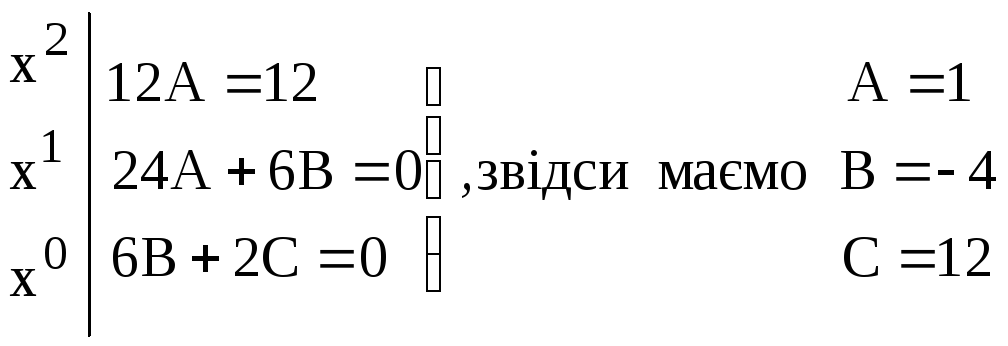рирівнюючи коефіцієнти при однакових степеняххв правій і лівій частинах рівності, одержимо:

Отже, у_част. =х⁴–4х³+ 12х², а загальний розвязок даного неоднорідного рівняння буде

у=у_одн+у_част= С₁+ С₂х+ С₃е^–х+х⁴–4х³+ 12х².

П р и к л а д 14. Проінтегрувати рівняння:

у –5у +6у = 13sin3х.

Р о з в я з о к. Коренями характеристичного рівнянняk²– 5 k + 6 = 0 будутьk₁= 2,k₃= 3, отже,

у_одн= С₁е^2х + С₂е^3х

Оскільки число і = 3і не є коренем характеристичного рівняння, тому частинний розвязок неоднорідного диференціального рівнянняу_частбудемо шукати у вигляді:

у_част = Аsin3x + Bcos3x

Знайдемо коефіцієнти А і В. Маємо:

у_част =3Аcos3x – 3Bsin3x

у_част = –9Аsin3x –9Bcos3x,

Підставляючи у_частіу_часту диференціальне рівняння, одержимо:

–9Аsin3x – 9Bcos3x – 15Аcos3x + 15Bsin3x + 6Аsin3x + 6Вcos3x13 sin3x.

П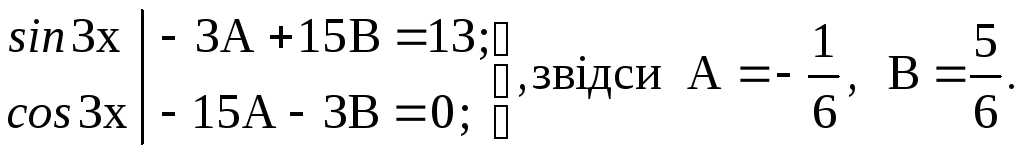рирівнюючи коефіцієнти приsin3x іcos3x, одержимо систему рівнянь:

Отже,

Загальний розвязок неоднорідного рівняння буде:

П р и к л а д 15. Розвязати рівняння:

у+4у = 3sin 2х.

Р о з в я з о к.

Характеристичне рівняння k²+4 = 0 має уявні кореніk_1,2=2і, тому

у_одн= С₁cos2х + С₂3sin 2х.

Оскільки 2і є коренем характеристичного рівняння, то частинний розвязок будемо шукати у вигляді:

у_част = (Аcos2x + Bsin2x)х.

Знаходимо похідні у_частіу_част:

у_част= (–2Аsin2x +2Bcos2x)х + Аcos2x + Вsin2x,

у_част= (–4Аcos2x – 4Вsin2x)х – 2Аsin2x + 2Bcos2x – 2Аsin2x + 2Bcos2x =

= (–4Аcos2x – 4Вsin2x)х – 4Аsin2x + 4Bcos2x.

Підставляючи у_частіу_часту дане диференціальне рівняння, одержимо:

(–4Аcos2x – 4Вsin2x)х – 4Аsin2x + 4Bcos2x + (2Acos2x + 4Вsin2x)х3sin2x ,

або – 4Аsin2x + 4Bcos2x = 3sin2x

П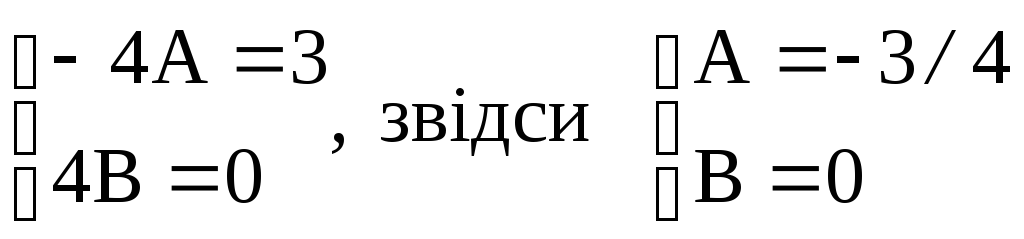рирівнюючи коефіцієнти приsin2xіcos2xу правій і лівій частинах, дістаємо систему:

Отже, у_част.=а загальний розвязок рівняння буде:

У = С₁ cos2x + С₂ sin2x.

П р и к л а д 16. Розвязати рівняння: у–2у + у = sinх + е^–х.

Р о з в я з о к. Корені характеристичного рівнянняk²– 2k+ 1= 0будутьk₁ =k₂ = 1. Отже, загальний розвязок однорідного рівняння буде

у_одн= С₁е^х+ С₂хе^х

Так як права частина рівняння f(x)складається із суми двох функційsinx і е^–х, то частинний розвязок у_част.будемо шукати у вигляді:

у_част.=у₁+у₂,

де у₁– частинний розвязок рівнянняу–2у+у=sinх,

у₂– частинний розвязок рівнянняу–2у+у= е^–х.

Знайдемо у₁:

у–2у+у=sinх (*)

Число і= iне є коренем характеристичного рівняння, тому частинний розвязок у₁будемо шукати у такому вигляді:

у₁=Asinx + Bcosx

Знаходимо похідні у₁і у₁:

у₁=Acosx–Bsinx, у₁= –Asinx–Bcosx

Підставляємо у₁, у₁іу₁в рівняння (*):

–Аsinx – Bcosх – 2Acosx+ 2Вsinx + Аsinx + Вcosxsinx.

П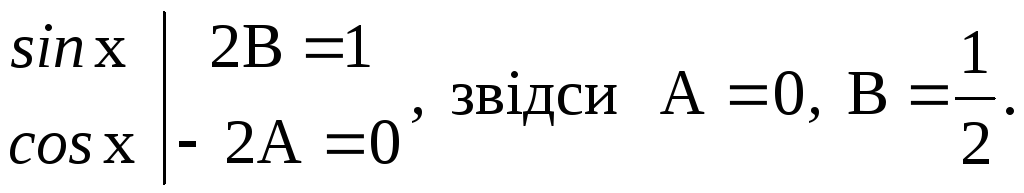рирівнюючи коефіцієнти приsinxіcosxв лівій і правій частинах тотожності, маємо:

Тепер знайдемо частинний розвязоку₂для рівнянняу–2у+у= е^–х(**)

Так як = –1 не є коренем характеристичного рівняння, то частинний розвязок у₂шукаємо у вигляді:

у₂= Ае^–х

Підставляючиу₂,у₂іу₂в рівняння (**), одержимо.

Таким чином, частинний розвязок даного диференціального рівняння буде

айого загальний розвязок буде: