- •V. Похідна і диференціал функції
- •5.1. Задачі, які приводять до поняття похідної
- •1. Миттєва швидкість руху.
- •2. Швидкість радіоактивного розпаду речовини.
- •4. Задача про силу струму.
- •5.Задача про кутовий коефіцієнт дотичної.
- •5.2. Означення похідної
- •5.3. Диференційовність та неперервність
- •Правила диференціювання
- •Диференціювання основних елементарних функцій
- •Отже, приріст функції і її диференціал є еквівалентними
- •5.13 Приклади диференціювання функцій
Правила диференціювання
10. Похідна сталої дорівнює нулю
![]()
Доведення проведемо за поданою раніше схемою.
За умовою
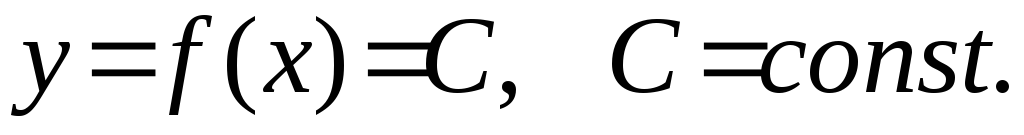
Для
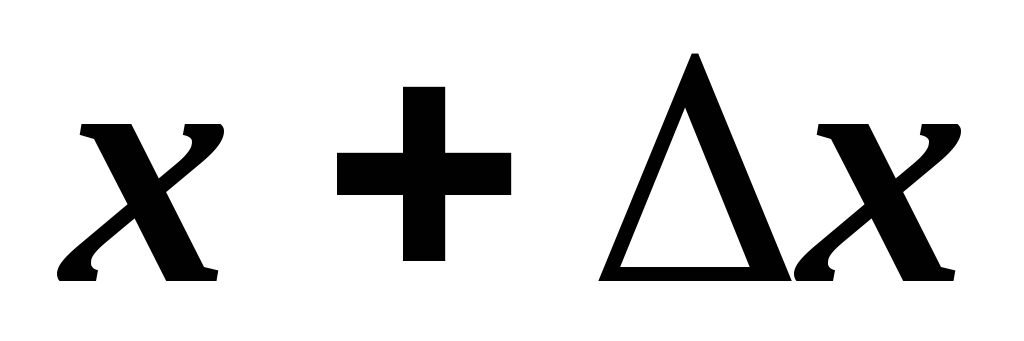 знаходимо
знаходимо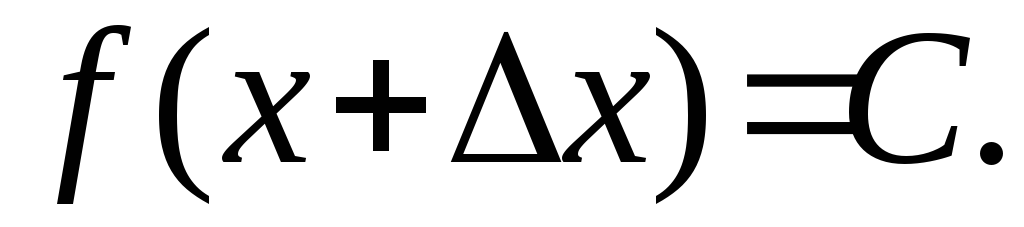
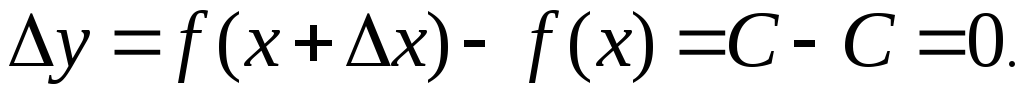
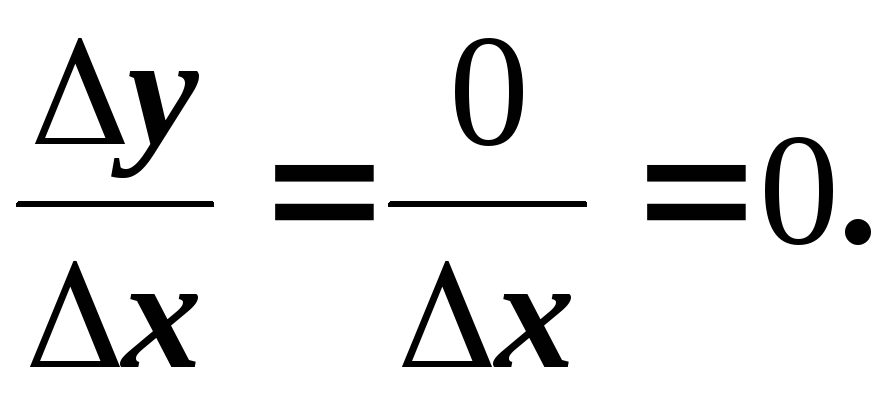
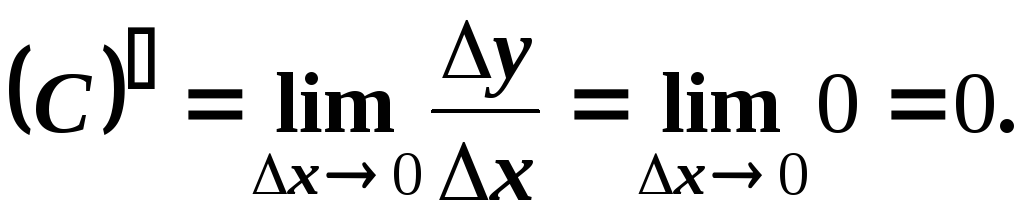
20. Похідна аргумента дорівнює 1, тобто
![]()
30. Похідна алгебраїчної суми диференційовних функцій дорівнює алгебраїчній сумі похідних цих функцій, тобто
![]()
Доведення.
Нехай функція
![]() мають похідні
мають похідні
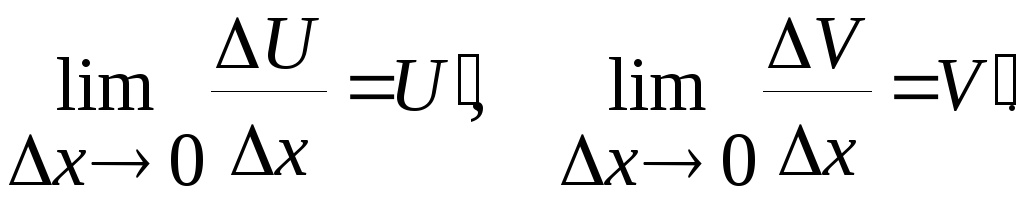
Розглянемо
функцію
![]() тоді
тоді
![]()
![]()
![]()
![]()
40. Похідна добутку двох диференційовних функцій дорівнює добутку похідної першого співмножника на другий без зміни плюс добуток першого співмножника без зміни на похідну другого співмножника, тобто
![]()
Доведення. Згідно схеми маємо:

надамо значенню х приріст
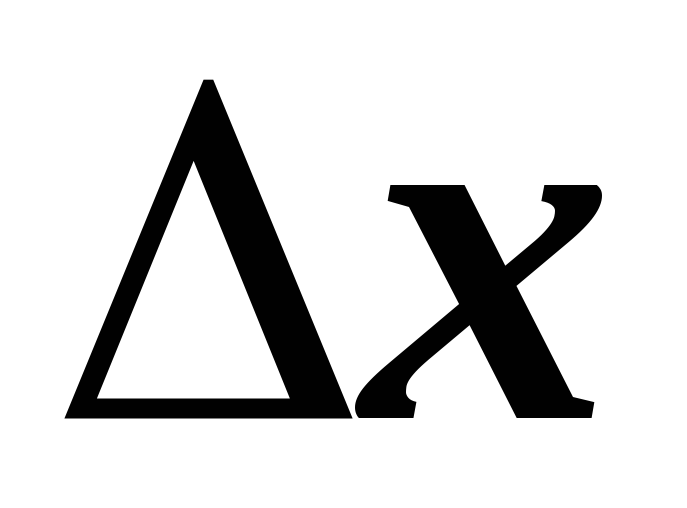 ,
тоді функції
,
тоді функції
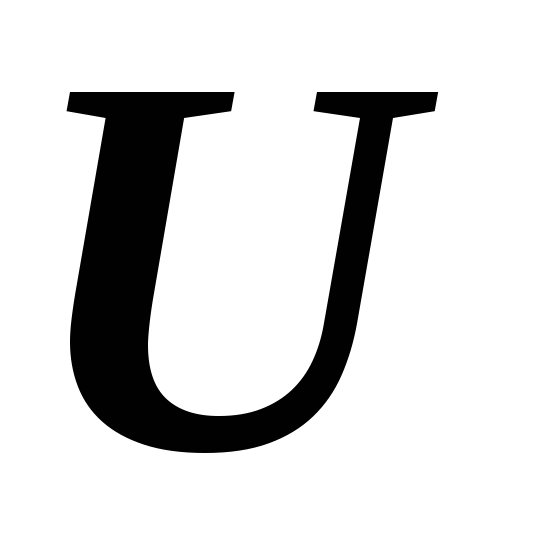 і
і
 набудуть нових значень
набудуть нових значень
 і
і
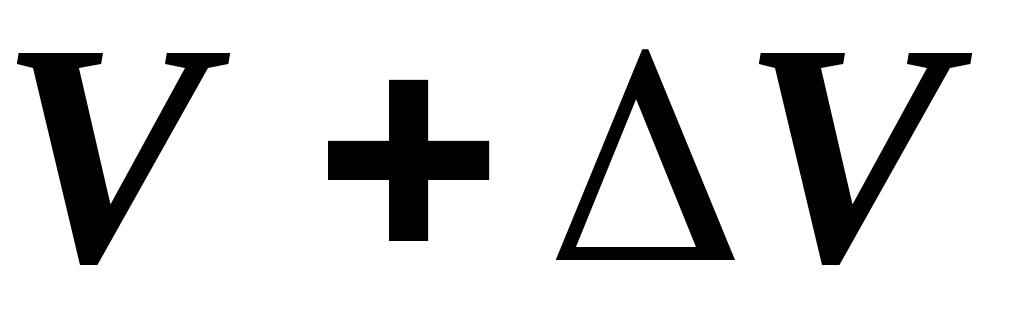 .
і нове значення добутку буде
.
і нове значення добутку буде
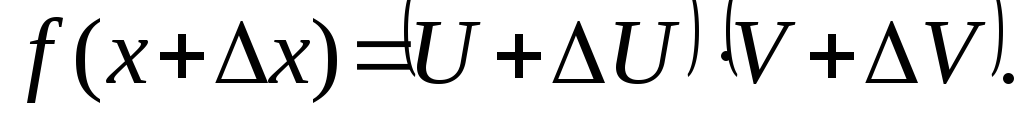
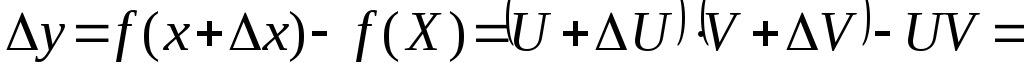
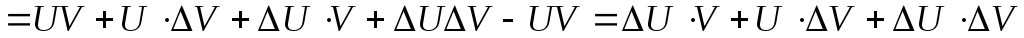 .
.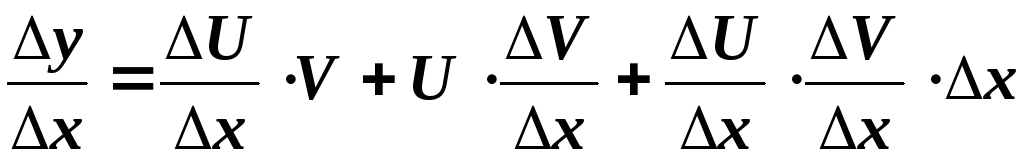 .
.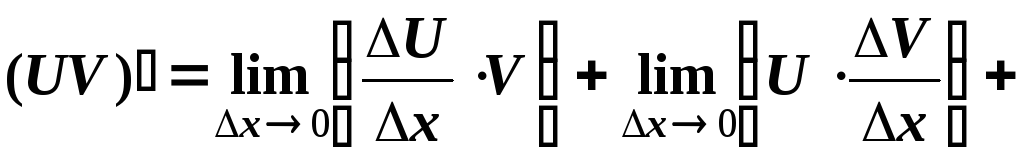
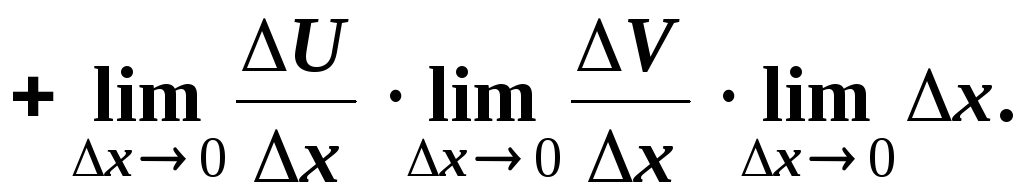
Оскільки
![]() і
і![]() від
від![]() не залежать, то їх можна виносити за
знак границі. Отже, формула похідної
добутку доведена.
не залежать, то їх можна виносити за
знак границі. Отже, формула похідної
добутку доведена.
Наслідок 1. Сталий множник можна виносити за знак похідної, тобто
 .
.
Дійсно,
згідно 10
і
40
маємо
![]() .
.
Наслідок 2. Для похідної добутку трьох співмножників маємо:
![]() .
.
Очевидно, що формулу можна узагальнити на більшу кількість співмножників.
50. Похідна степеневої функції знаходиться за формулою
![]()
Доведемодляnнатурального
![]()
![]()
Випадок довільного дійсного nбуде розглянутий далі.
60. Похідна частки двох диференційовних функцій має вигляд
![]() .
.
За
умови, що
![]()
Доведення аналогічне правилу 40.
Приклади.Знайти похідні
![]()
![]()
![]()
![]()
![]()
![]()
5.5 Похідна складної і оберненої функції
Розглянемо![]() ,
або
,
або
![]() ,
- складну функцію, деU
– проміжна зміна,
,
- складну функцію, деU
– проміжна зміна,
![]() – незалежна зміна.
– незалежна зміна.
Теорема 1.Нехай
![]() ,
і
,
і![]() - диференційовні у відповідних точках
функції, тоді похідна складної функції
існує і дорівнює добуткові даної функції
по проміжній змінній на похідну проміжної
змінної по незалежній змінній, тобто
- диференційовні у відповідних точках
функції, тоді похідна складної функції
існує і дорівнює добуткові даної функції
по проміжній змінній на похідну проміжної
змінної по незалежній змінній, тобто
![]() (1)
(1)
Доведення.Згідно викладених в5.3міркувань
із умови існування похідної маємо![]()
де
![]() при
при
![]() .
Розділивши останню рівність на
.
Розділивши останню рівність на
![]() ,
знаходимо
,
знаходимо
![]() (2)
(2)
Із умови диференційовності функції
![]() випливає її неперервність, тобто із
випливає її неперервність, тобто із![]() ,
а, значить,
,
а, значить,![]() тому в результаті граничного переходу
в(2)при
тому в результаті граничного переходу
в(2)при![]() отримаємо
отримаємо![]()
Наслідок.Для степеневої функції![]() де
де![]() маємо:
маємо:
![]() (3)
(3)
П
За
формулою (4)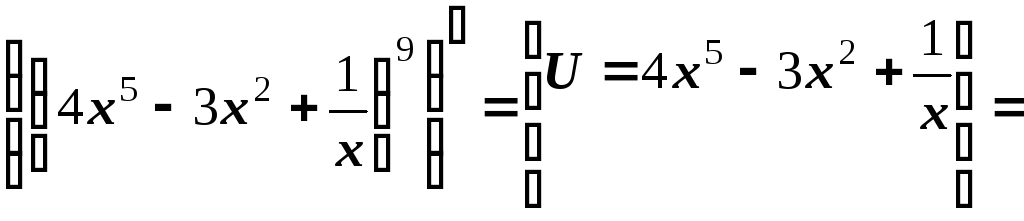
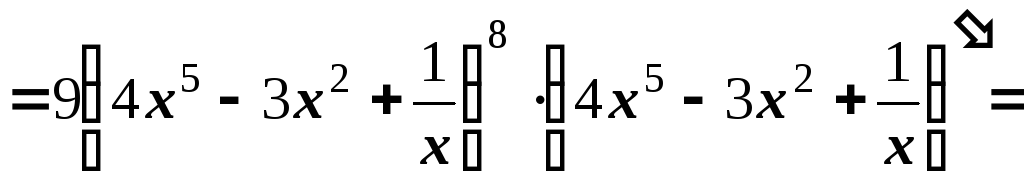
![]()
5.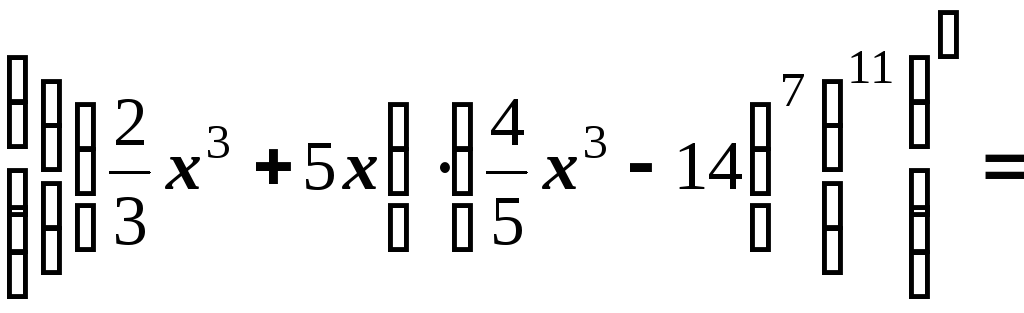
![]()
![]()
Перейдемо до розгляду похідної оберненої функції
Нехай
![]() - диференційовна і строго монотонна на
деякому проміжку осіOX.
Як вже відмічалося (див.2.4): якщо
- диференційовна і строго монотонна на
деякому проміжку осіOX.
Як вже відмічалося (див.2.4): якщо![]() неперервна, то для неї існує обернена
функція
неперервна, то для неї існує обернена
функція![]() теж неперервна на відповідному проміжку
по змінній
теж неперервна на відповідному проміжку
по змінній![]() .
.
Теорема 2. Для диференційовної функції з похідною, відмінною від нуля, існує похідна оберненої функції, яка дорівнює оберненій величині похідної даної функції, тобто
![]() . (4)
. (4)
Доведення.Нехай![]() - приріст змінної
- приріст змінної![]() ,
якому відповідає приріст
,
якому відповідає приріст![]() оберненої функції
оберненої функції![]() .
Тоді правильна рівність
.
Тоді правильна рівність
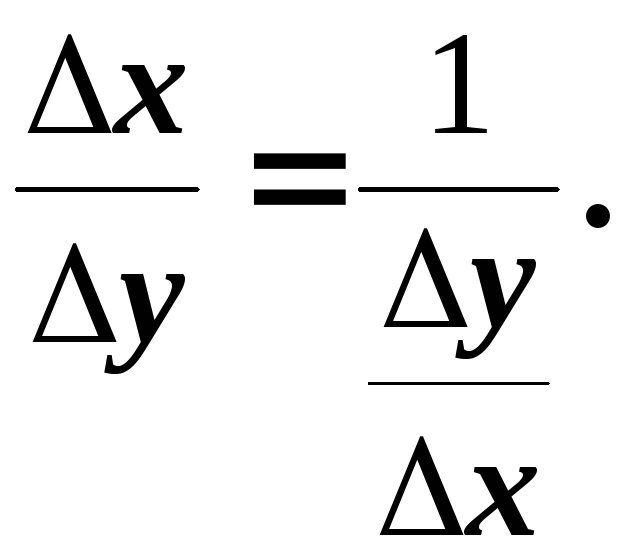
Перейшовши
до границі при
![]() ,
і враховуючи, що згідно неперервності
оберненої функції
,
і враховуючи, що згідно неперервності
оберненої функції![]() ,
маємо
,
маємо
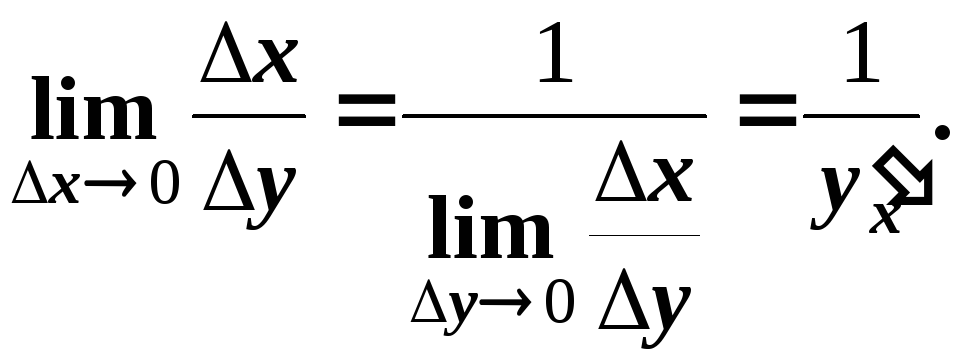
Наприклад,
функція
![]() має обернену
має обернену![]() для
для![]() ,
тоді
,
тоді
![]()
А тепер розглянемо
За
умовою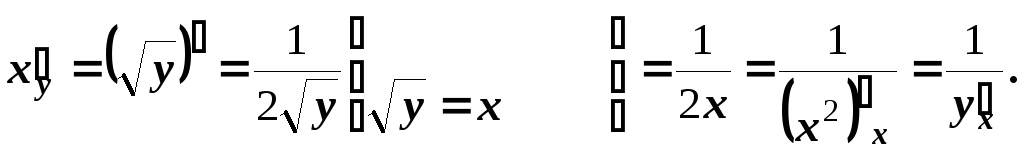
Диференціювання основних елементарних функцій
5.6.1 Похідна
логарифмічної функції
![]()
Похідну знаходимо за схемою:
1)
![]() .2)
.2)![]()
3)
![]()
Ураховуючи
властивість еквівалентності нескінченно
малих
![]() при
при![]() маємо
маємо
![]()
4)
Знаходимо
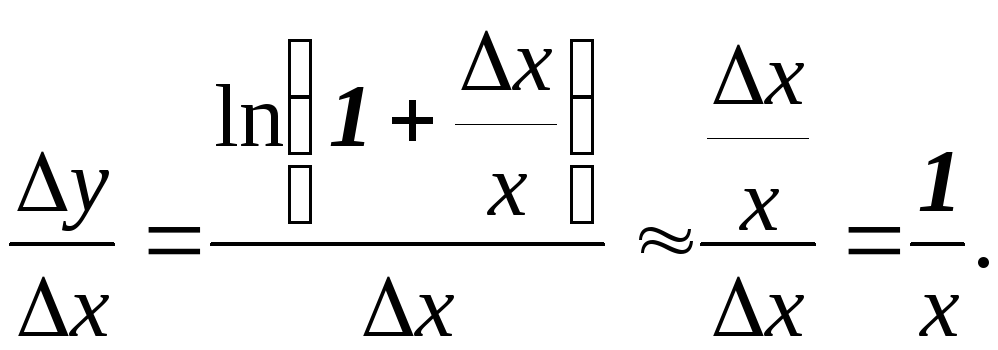
![]()
Для
складної функції
![]()
б)![]() .
За формулою переходу в логарифмах до
нової основи
.
За формулою переходу в логарифмах до
нової основи![]() маємо ,
маємо ,
![]() ,
,
тобто,
![]()
5.6.2 Похідна
показникової функції
![]()
В
результаті логарифмування обох частин
маємо
![]()
![]()
Отже,
![]()
б)
![]() Згідно тотожності
Згідно тотожності![]() маємо
маємо
![]()
![]() ,
,
тобто,
![]()
5.6.3 Похідна
степеневої функції
![]() ,
де
,
де![]() - довільне дійсне число
- довільне дійсне число
Аналогічно попередньому
![]()
![]()
![]()
![]() - довільне дійсне число. Зокрема, якщо
- довільне дійсне число. Зокрема, якщо![]() ,
то
,
то
![]() тому
тому![]()
![]()
Аналогічно,
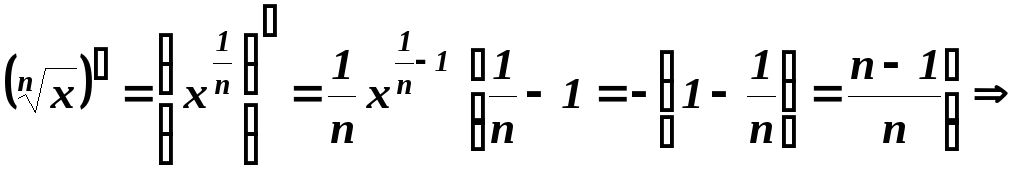
![]()
5.6.4 Похідні тригонометричних функцій
 Згідно означення маємо
Згідно означення маємо
![]()
![]()
![]()
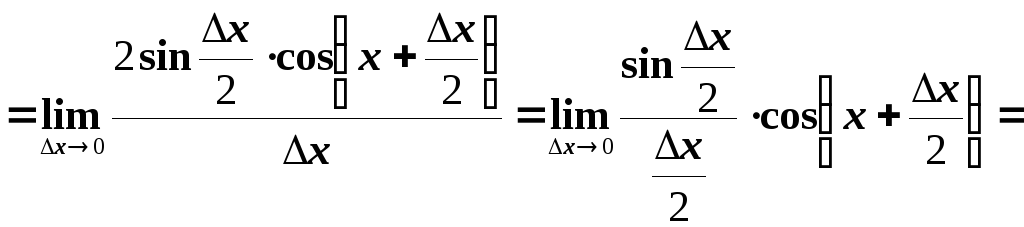
![]()
Отже,
![]()
2. ![]() Із тригонометрії відомо, що
Із тригонометрії відомо, що![]() ;
;![]() ,
тому
,
тому![]()
![]()
3. ![]()
![]()
![]()
![]()
![]()
5.6.5 Похідні обернених тригонометричних функцій
1. ![]() Переходимо до оберненої функції
Переходимо до оберненої функції![]() і диференціюємо обидві частини, причому
зліва як складну функцію,
і диференціюємо обидві частини, причому
зліва як складну функцію,![]()
![]()
![]()
![]() 2.
2.
![]() .
З тригонометрії відомо, що
.
З тригонометрії відомо, що![]() тому
тому
![]() .
.
3.
![]()
![]()
![]()
![]()
![]()
5.6.6 Похідна
степенево-показникової функції
![]() ,
де
,
де![]() - диференційовні функції. Знайдемо
логарифми рівності
- диференційовні функції. Знайдемо
логарифми рівності![]() і продиференціюємо обидві частини
і продиференціюємо обидві частини
![]()
![]()
![]() .
.
Приклади.Знайти похідні
1)
![]()
![]()
![]()
![]()
2.
![]()
![]()
![]()
![]()
5.6.7 Похідна неявної функції
Функцію у аргумента х називають неявною, якщо вона задана рівнянням F(x,y)=0, яке не розв’язане відносно залежної змінної.
Наприклад,
![]() задає неявно дві функції
задає неявно дві функції
![]() ,
якщо
,
якщо
![]() ,
і
,
і
![]() якщо
якщо
![]() .
.
Неявні функції диференціюють як складні.
![]()
![]() (1)
(1)
Переконаємось
на прикладі функції
![]() при
при
![]() ,
що похідна її збігається з отриманим
виразом (1). Дійсно,
,
що похідна її збігається з отриманим
виразом (1). Дійсно,

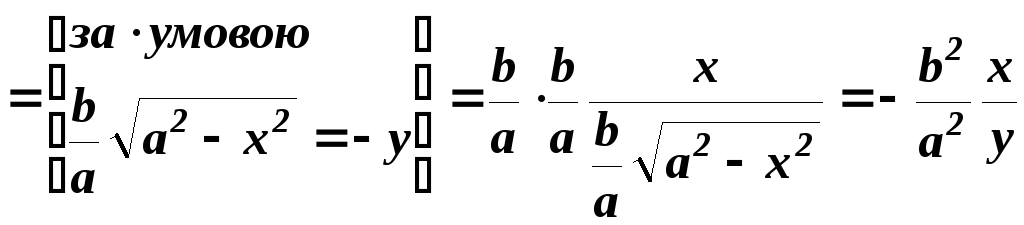 .
.
Приклад.
Знайти
![]() ,
якщо
,
якщо
![]()
Диференціюючи рівність, отримуємо
![]()
![]()
![]()
5.7 Таблиця похідних
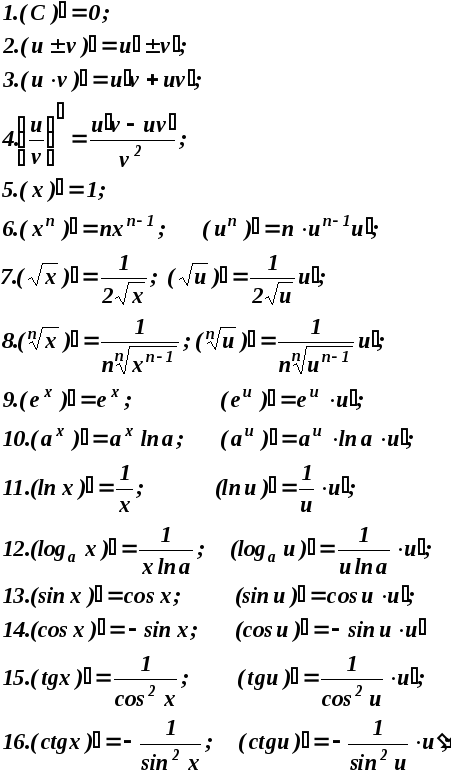
![]()

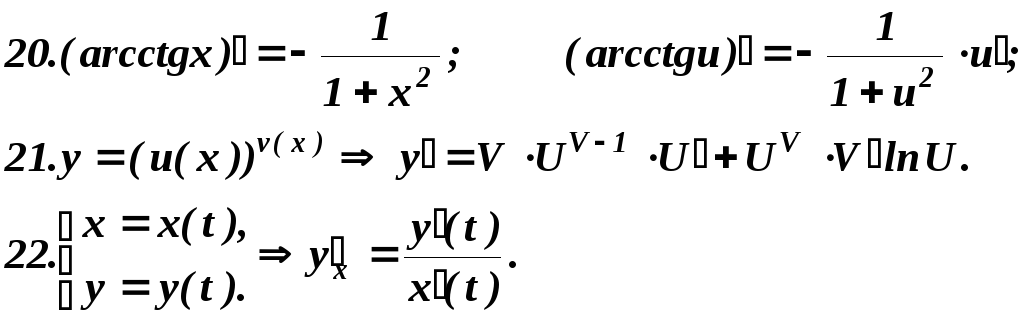
5.8. Означення диференціала функції
Нехай функція y=f(x) диференційовна в точці х, тобто існує границя
![]()
Згадаємо властивість про зв’язок функції з її границею, а саме:
якщо,
![]() ,
то
,
то![]() прихх0,
де (х)
нескінченно мала величина. Тому початкове
співвідношення (8) можна записати:
прихх0,
де (х)
нескінченно мала величина. Тому початкове
співвідношення (8) можна записати:
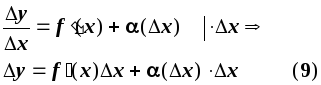
де (х)0 – нескінченно мала величина при х0. Співвідношення (9) показує, що приріст функції складається з двох доданків: (х)х – нескінченно малої величини вищого порядку малості при х0 в порівнянні з f(x)x (f(x)0). Тому f(х)х є головною частиною приросту функції, лінійною відносно х.
Означення. Головна, лінійна відносно х, частина приросту функції називається диференціалом функції і позначається
dy = f(x)x. (10)
Якщо в (10) взяти у=х , то dy=(x)x dy=x, але y=x, тому
d x = x –
для незалежної змінної х її диференціал збігається з приростом. В зв’язку з цим формула (10) приймає вигляд:
dy = f(x)dx – (11)
-формула диференціла функції.
З
формули (11) маємо
![]() ще
одне пояснення позначення похідної.
ще
одне пояснення позначення похідної.
Розділимо
почленно співвідношення (9) для приросту
функції на
![]() і
знайдемо границю прих0.
і
знайдемо границю прих0.
![]()