разрешимость в радикалах

Разрешимость уравнений в радикалах

Определение. Пусть P – числовое поле, - число. Говорят, что выражается в радикалах над полем P ,если оно выражается через числа поля P с помощью нахождения корней произвольной степени и рациональных операций суммы, произведения, деления и разности. Другими словами, выражается в радикалах над полем P ,если существует последовательность такая, что для произвольного k верно одно из условий:

1. ,

2. , или , или , или , где i<k,j<k;

3. .

Пример. P=Q. - выражается в радикалах над Q: .

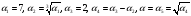Определение. Алгебраическое уравнение с коэффициентами из P называется разрешимым в радикалах над P, если все его корни выражаются в радикалах над P.

Определение. Число выражается в квадратичных (квадратных) радикалах над полем P, если оно выражается через числа поля P с помощью нахождения квадратных корней и рациональных операций.

Определение. Алгебраическое уравнение с коэффициентами из P называется разрешимым в квадратичных радикалах над P, если все его корни выражаются в квадратичных радикалах над P.

Теорема. Пусть - полином, неприводимый над P, при этом . Если n не является степенью двойки, то ни один из корней этого полинома не выражаются в квадратичных радикалах над P.

Доказательство. От противного. Пусть - корень , который выражаются в квадратичных радикалах над P, т.е. существует последовательность из первого определения (r=2).

Построим последовательность расширений: .

Для любого k рассмотрим расширение . Если , то , если , то . Таким образом, .

Если 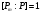, то , тогда , т.е. полином приводим – противоречие.

Если , то рассмотрим цепочку расширений . Данные расширения конечные. Тогда , т.е. (так как - корень неприводимого полинома степени n), из чего следует, что n является степенью двойки. Противоречие. Теорема доказана.

Следствие*. Пусть , . Уравнение разрешимо в квадратичных радикалах над P тогда и только тогда, когда один из корней этого полинома принадлежит полю P.

Доказательство. Самостоятельно.

Геометрические построения с помощью циркуля и линейки. Необходимое и достаточное условия разрешимости задач на построение.

Пусть задано некоторое конечное множество точек М. Тогда:

1.Если точка A принадлежит M, то точку A можно построить.

2. Если точки A и B можно построить, то прямую AB можно построить.

3. Если точки O и A можно построить, то можно построить окружность с центром в точке O радиуса OA.

4. Если можно построить пересекающиеся прямые l и m, то можно построить их точку пересечения.

5. Если можно построить прямую l и окружность O, имеющие общие точки, то можно построить любую их общую точку.

6. Если можно построить окружности O и O', имеющие общие точки, то можно построить любую их общую точку.

7. Никакие другие точки нельзя построить.

Пусть задано множество М точек плоскости, которое содержит 2 точки А и А^'. Через них можно провести прямую. Пусть А-0, А^’ – 1. С помощью циркуля и линейки можно построить прямую, проходящую через 0 и перпендикулярную АА’. На ней построим АB= АА’. Получим декартову систему координат.

С одной стороны, точки плоскости можно отождествлять с комплексными числами.

С другой стороны, Точку М(a;b) можно рассматривать как точку плоскости R². Построить точку М – значит построить отрезки, длины которых равны a и b.

В таком случае можно построить:

a+b, a-b (если a<b, то (b-a) построим в противоположном направлении оси), a*b, b/a, .

Следствие. Если построены точки a и b, то с помощью циркуля и линейки можно построить любые элементы из расширения Q(a,b).

Далее будем отождествлять плоскость с R². Точка М(a.b) определена над полем P, если ее координаты принадлежат P.

Свойство. Если точки A₁(x₁,y₁), A₂(x₂,y₂) определены над P, то прямую, проходящую через них, можно записать в виде: ax+by=c, где .

Доказательство. Уравнение прямой: , причем .

Свойство. Если точки A₁(x₁,y₁), A₂(x₂,y₂) определены над P, то окружность с радиусом и центром в точке A₁, задается уравнением .

Доказательство. Аналогично.

Свойство. Пусть заданы прямые ax+by=c и dx+ey=f, где . Координаты точки их пересечения определены над P.

Доказательство. Аналогично(решить систему и найти координаты точки пересечения).

Свойство. Пусть заданы прямая ax+by=c и окружность .Тогда точка (точки) их пересечения определена либо над P, либо над .

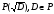Доказательство. . Если b=0, то получим аналогичный результат.

Свойство. Пусть заданы две окружности. Тогда точка (точки) их пересечения определена либо над P, либо над .

Теорема1. Пусть М – множество точек, определенных над P. Для того, чтобы можно было построить с помощью циркуля и линейки некоторые точки, необходимо и достаточно, чтобы это число принадлежало некоторой цепочке квадратичных расширений .

Доказательство.

Необходимость. Пусть задано непустое множество М. Из предыдущих свойств следует, что построенные числа принадлежат либо P, либо цепочке .

Достаточность. Так как a и b из P, то, по рассмотренному ранее, a+b, a-b, a*b, b/a, (т.е. все элементы из ) можно построить с помощью циркуля и линейки. Следовательно, любой элемент из можно построить.

Неразрешимые задачи на построение.

Задача о квадратуре круга. Построить квадрат, равновеликий данному кругу.

Пусть радиус данного круга равен 1 (т.к. можно взять любой масштаб). . Площадь круга равна: . Таким образом, нужно построить a. По теореме1 это можно сделать тогда и только тогда, когда 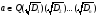, т.е. конечному расширению Q, тогда a – алгебраическое число. Следовательно, - алгебраическое. Противоречие. Таким образом, такой квадрат построить с помощью циркуля и линейки нельзя.

Задача о трисекции угла. Поделить произвольный угол на три равные части.

Пусть дан угол . Нужно построить угол . Построение угла эквивалентно построению косинуса этого угла. . Пусть . Тогда нужно выяснить, можно ли построить корни данного уравнения: , так как является его корнем. Имеем: . Уравнение не имеет рациональных корней, значит (следствие*). Построить данный угол нельзя.

Таким образом, не любой угол можно построить с помощью циркуля и линейки. (Но некоторые можно. Например, угол 90⁰).

Задача о делении круга на n равных частей. (построение правильного n- угольника).

Дана окружность. Вписать в нее правильный n-угольник.

См в предложенных статьях.