
- •Министерство образования и науки Российской Федерации
- •Тобольск – 2012
- •Глава I. Великая теорема ферма и алгебраические числа
- •§ 1. Предварительные сведения
- •§ 2. Диофантовы уравнения, пифагоровы тройки и Великая теорема Ферма
- •§ 3. Метод бесконечного спуска и доказательство
- •§ 4. Сводка результатов: от Эйлера до Куммера
- •Глава II. Великая теорема ферма и abc-гипотеза
- •§ 1. Гипотеза Таниямы и доказательство Вайлса
- •Великой теоремы Ферма
- •§ 2. Abc-гипотеза и “Великая теорема Ферма” для многочленов
- •§ 3. Abc-гипотеза для натуральных чисел
- •§ 4. Некоторые следствия abc- и (abc)2- гипотез
§ 2. Диофантовы уравнения, пифагоровы тройки и Великая теорема Ферма
Диофантово уравнение – это уравнение вида P(x1 , … , xn) = 0, где левая часть представляет собой многочлен от переменных x1 , … , xn с целыми коэффициентами. Любой упорядоченный набор (u1 ; … ; un) целых чисел со свойством P(u1 , … , un) = 0 называется (частным) решением диофантова уравнения P(x1 , … , xn) = 0. Решить диофантово уравнение – значит найти все его решения, или, как говорят, общее решение этого уравнения. Часто диофантовыми называют и уравнения вида P(x1 , … , xn) = Q(x1 , … , xn), где в левой и правой частях стоят многочлены от переменных x1 , … , xn : их всегда можно записать в виде диофантовых уравнений P(x1 , … , xn) – Q(x1 , … , xn) = 0.
Эти уравнения названы в честь Диофанта Александрийского (жил около III в. до РХ), о жизни которого почти ничего не известно. Через века до нас дошли шесть книг из тринадцати его главного труда “Арифметика” и книга “О многоугольных числах”. Выражаясь современным языком, он разрабатывал приёмы нахождения рациональных решений алгебраических уравнений от нескольких неизвестных.
Примеры:
1.
3x
– 8 = 0 – диофантово
уравнение первой степени от одной
переменной x.
Очевидно, что оно не имеет решений, т.к.
8
не делится нацело на 3.
В то же время, это уравнение имеет корень
x
=
![]() , который
не является целым.
, который
не является целым.
2. Диофантово уравнение 6x = 24 имеет единственное решение x = 4.
3. В курсе алгебры и теории чисел рассматривают линейные диофантовы уравнения первой степени от двух неизвестных x, y, общий вид которых таков: ax + by = c, где a, b, c – заданные целые числа. Известно, что такое диофантово уравнение имеет решение тогда и только тогда, когда НОД(a, b) | c – наибольший общий делитель коэффициентов делит нацело правую часть. При выполнении этого условия линейное диофантово уравнение от двух переменных имеет бесконечное число решений.
Нахождение решений произвольных диофантовых уравнений – непростая задача. Более того, в 70-х годах XX в. было доказано, что она алгоритмически неразрешима, т.е. невозможно придумать алгоритм (программу для ЭВМ), который для произвольного заданного диофантова уравнения давал бы ответ на вопрос: “Есть у этого уравнения хотя бы одно решение ?”.
Тем удивительнее, что для некоторых классов диофантовых уравнений можно получить полное описание их решений. Классической задачей такого рода, обсуждаемой в “Арифметике” Диофанта, является задача о пифагоровых тройках, т.е. о нахождении всех решений диофантова уравнения x2 + y2 = z2 , представляющего собой соотношение Пифагора для прямоугольного треугольника. Вначале найдём все его рациональные решения, а затем – и все целые решения.
1. Рациональные
решения уравнения Пифагора.
Во-первых, уравнение переписывается в
виде
![]() , где отношения
, где отношения
![]() ,
,![]() рациональны,
если рациональными были x,
y.
Эти отношения являются рациональными
координатами точек на единичной
окружности. Точки с рациональными
координатами на окружности назовём
рациональными.
Если все рациональные точки M(u;
v)
окружности
уже описаны, то u2
+ v2
= 1 и
рациональны,
если рациональными были x,
y.
Эти отношения являются рациональными
координатами точек на единичной
окружности. Точки с рациональными
координатами на окружности назовём
рациональными.
Если все рациональные точки M(u;
v)
окружности
уже описаны, то u2
+ v2
= 1 и
![]() =u,
=u,
![]() =v,
т.е. x
= zu,
y
= zv
, где z
Q
. Таким
образом, задача нахождения всех
рациональных решений уравнения Пифагора
свелась к описанию всех рациональных
точек окружности.
=v,
т.е. x
= zu,
y
= zv
, где z
Q
. Таким
образом, задача нахождения всех
рациональных решений уравнения Пифагора
свелась к описанию всех рациональных
точек окружности.
Изложим общий метод нахождения всех рациональных точек окружности, применимый и для многих других кривых, заданных полиномиальными уравнениями.
В ыберем
на кривой рациональную точку, например
точкуS(0;
–1) на
окружности (рис. 1). Если M(u;
v)
– произвольная рациональная точка, то
рациональным будет и
ыберем
на кривой рациональную точку, например
точкуS(0;
–1) на
окружности (рис. 1). Если M(u;
v)
– произвольная рациональная точка, то
рациональным будет и
![]() .
.
Обратно, если t
Q
, то u
= t(v
+ 1) и u2
+ v2
= 1, т.е.
t2(v
+ 1)2
+ v2
= 1 или
(t2+1)v2+2t2v+t2-
1= 0. Здесь
дискриминант D
= 4t4
– 4(t4
– 1) = 4 и
![]() . Если взять знак минус, то получим v
= –1, u
= t(v
+ 1) = 0, т.е.
точку S(0;
–1). Если же
брать плюс, то
. Если взять знак минус, то получим v
= –1, u
= t(v
+ 1) = 0, т.е.
точку S(0;
–1). Если же
брать плюс, то
![]()
Q
.
Q
.
Таким образом,
доказано, что точка на окружности
рациональна тогда и только тогда, когда
она либо совпадает с S(0;
–1), либо
получается по формулам
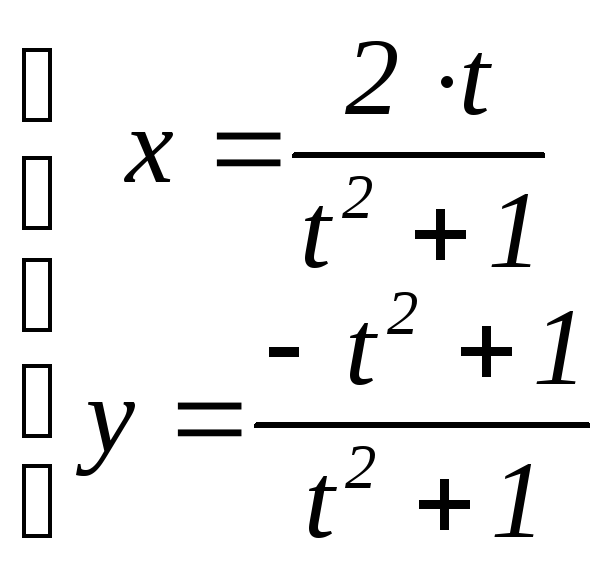 при некотором t
Q
.
при некотором t
Q
.
Легко понять, что
точка S(0;
–1) не может
быть получена по приведённым формулам
ни при каком рациональном t.
Можно видоизменить параметризацию,
чтобы включить точку S
в общие решения. Для этого запишем
число t
Q
в несократимом
виде
![]() , где m
Z,
n
N
, НОД(m,
n)
= 1. Тогда
формулы перепишутся так:
, где m
Z,
n
N
, НОД(m,
n)
= 1. Тогда
формулы перепишутся так:
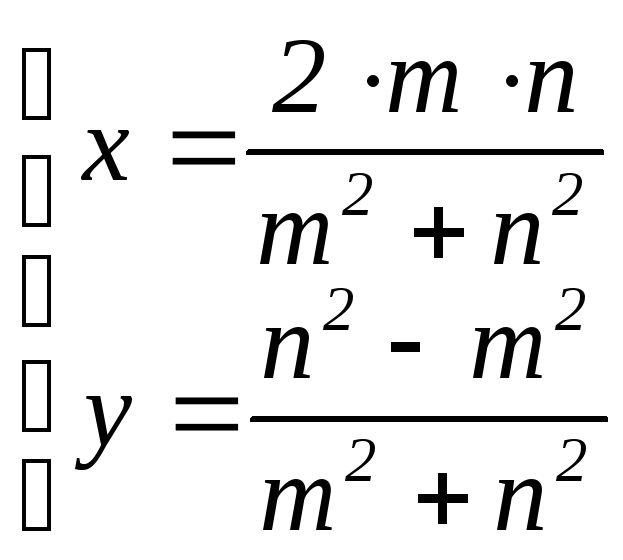 . Они
определены при любых m,
n
Z
и при n
= 0 дают точку
S(0;–1).
Таким образом, доказана следующая
теорема:
. Они
определены при любых m,
n
Z
и при n
= 0 дают точку
S(0;–1).
Таким образом, доказана следующая
теорема:
Теорема (о рациональных точках на окружности). (1) Все рациональные точки M(x; y) единичной окружности имеют координаты
![]() ,
,
при некоторых m, n Z , НОД(m, n) = 1.
(2) Все рациональные
пифагоровы тройки, т.е. рациональные
решения уравнения x2
+ y2
= z2
задаются формулами
![]() , где m,
n
Z
и НОД(m,
n)
= 1, z
Q
.
, где m,
n
Z
и НОД(m,
n)
= 1, z
Q
.
2. Целые решения уравнения Пифагора. Рассмотрим диофантово уравнение x2 + y2 = z2 от трёх неизвестных x, y, z. Оно, конечно, имеет решения: например, (0; 0; 0), (0; 1; 1), (3; 4; 5) и множество других. Решения, в которых одно из чисел равно нулю, называются тривиальными. Ясно, что все тривиальные решения имеют вид: (0; y; ±y), (x; 0; ±x), где x, y Z . Поэтому достаточно искать только нетривиальные решения.
Назовём решение (x; y; z) примитивным, если любые два числа в нём взаимно просты, т.е. если НОД(x, y) = НОД(x, z) = НОД(y, z) = 1. Ясно, что если есть некоторое решение (x; y; z) и D = НОД(x, y, z), то x = Dx1 , y = Dy1 , z = Dz1 при некоторых целых x1 , y1 , z1 , причём ввиду x2 + y2 = z2 получаем, сокращая на D2, x12 + y12 = z12, т.е. тройка (x1 ; y1 ; z1) тоже является решением. Кроме того, это решение примитивно: если НОД(x, y) = d > 1, то x1 = dx2 , y1=dy2 , d2(x22+y22)= z12 и число z1 делится на любой простой делитель p числа d, вопреки взаимной простоте чисел x1 , y1 , z1 . Аналогично рассматриваются и другие случае НОД(x, z) > 1, НОД(y, z) > 1.
Итак, доказано, что любое решение уравнения Пифагора получается из примитивного умножением всех его компонент на некоторое натуральное число D. Поэтому достаточно искать лишь примитивные пифагоровы тройки. Поскольку каждая такая тройка состоит из рациональных чисел, то можно применить описание рациональных пифагоровых троек.
Прежде всего, заметим, что из x2 + y2 = z2 следует, что одно из чисел x, y чётно, а другое нечётно. Действительно ввиду примитивности тройки x, y не могут быть чётными одновременно. Если x, y оба нечётны, то x2 + y2 чётно, т.е. z чётно и x2 + y2 делится на 4, что ведёт к противоречию: если x=2u+1, y = 2v + 1 (u, v Z), то x2 + y2 = 4(u2 + u + v2 + v) + 2 и не делится на 4.
Поменяв, если
нужно, x,
y
местами
(уравнение Пифагора симметрично по
x,
y),
будем считать, что x
чётно, а y
нечётно.
Согласно предыдущей теореме, каждая
примитивная тройка (x;
y;
z)
имеет вид
![]() при целых
z,
m,
n,
НОД(m,
n)
= 1. Значит,
x(m2
+ n2)
= z2mn,
причём числа x
и z
взаимно простые. По основному свойству
взаимно простых чисел получаем m2
+ n2
= zt
(t
Z)
и
xt
=2mn,
y
=
при целых
z,
m,
n,
НОД(m,
n)
= 1. Значит,
x(m2
+ n2)
= z2mn,
причём числа x
и z
взаимно простые. По основному свойству
взаимно простых чисел получаем m2
+ n2
= zt
(t
Z)
и
xt
=2mn,
y
=
![]() , т.е. m2
– n2
= yt
.
Отсюда
2m2
= (z + y)t,
2n2
= (z – y)t,
т.е.
t
– общий
делитель чисел 2m2
и 2n2.
Поэтому t
делит
НОД(2m2,
2n2)=2НОД(m2,n2)=2.
, т.е. m2
– n2
= yt
.
Отсюда
2m2
= (z + y)t,
2n2
= (z – y)t,
т.е.
t
– общий
делитель чисел 2m2
и 2n2.
Поэтому t
делит
НОД(2m2,
2n2)=2НОД(m2,n2)=2.
Если t = ±2, то m2 + n2 = ±2z 2, т.е. взаимно простые числа m, n оба нечётны, и кроме того, ±2x = 2mn, т.е. x= ±mn – нечётно, вопреки выбору x.
Значит, t = ±1, x = ±2mn, y = ±(m2 – n2), z = ±(m2 + n2), где целые числа m, n взаимно простые разной чётности (иначе y чётно), а комбинации знаков могут быть любыми. Учитывая возможность поменять местами x, y, получаем ещё возможность x = ±(m2 – n2), y = ±2mn, z = ±(m2 + n2). Любая целочисленная тройка получается одновременным умножением компонент описанных выше примитивных троек на произвольное целое число.
Легко проверить непосредственно, что найденные тройки действительно являются пифагоровыми: так, для x = ±(m2 – n2), y = ±2mn, z = ±(m2 + n2) получаем
x2 + y2 = (m2 – n2)2 + (2mn)2 = m4 – 2m2n2 + n4 + 4m2n2 =
= m4 + +2m2n2 + n4 = (m2 + n2)2 = z2 .
Таким образом, доказана
Теорема (о пифагоровых тройках). Любая пифагорова тройка имеет один из следующих видов:
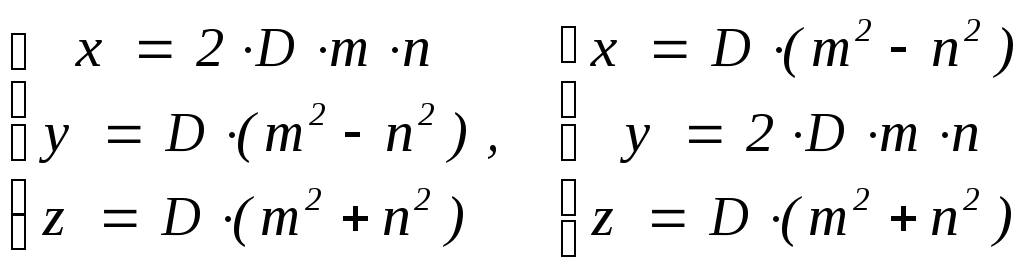 ,
,
где D, m, n – целые числа, m и n взаимно простые разной чётности.
Именно сочинение Диофанта “Арифметика”, изданное в 1621 году в переводе Клода Гаспара де Баше де Мазирьяка (1581-1630), в котором исследовались рациональные и целые решения уравнения Пифагора, дало повод Пьеру Ферма записать на полях этого перевода одно из самых достопримечательных замечаний в истории математики:
“Невозможно разложить куб на два куба, или биквадрат на два биквадрата, или вообще степень, большую двух, на две степени с тем же самым показателем; я нашел этому поистине чудесное доказательство, однако поля слишком малы, чтобы оно здесь уместилось”. Таким образом, большая или Великая теорема Ферма утверждает, что уравнение xn + yn = zn, ни при каком натуральном n, большем двух, неразрешимо в натуральных числах.
К сожалению, сам Ферма не оставил своего чудесного доказательства, в его записках было обнаружено обоснование лишь частного случая этой теоремы для n = 4. Долгие годы все усилия по доказательству Великой теоремы Ферма были тщетны, продвижения начали появляться лишь, начиная с XVIII в.: Л. Эйлер доказал теорему Ферма для n = 3 (1770 г), А. Лежандр – при n = 5 (1825 г), и Г. Ламе – для n = 7 (1839 г).
В 1908 году Пауль Вольфскель завещал премию в 100 тысяч германских марок тому, кто первым представит доказательство. В результате инфляции после первой мировой войны величина премии в настоящее время ничтожна. К тому же как указывает Г. Эдвардс в своей книге о теореме Ферма [5], премия была назначена лишь за доказательство предположения – нахождение контрпримера не принесло бы ни пфеннига его открывателю !
После объявления о премии Великой теоремой Ферма занялись не только профессионалы, но и широкая публика. Так как в условие награждения входило требование, чтобы доказательство было опубликовано, а научные издательства не желали принимать ложных доказательств, то авторы печатали свои доказательства на собственный счет. Так во многих странах, в том числе и в России, появилось много печатных неправильных доказательств Великой теоремы Ферма.
Общим свойством этих “доказательств” является то, что они ошибочны уже для наименьшего показателя в теореме Ферма, а именно, для показателя n = 3. Авторы этих работ, преимущественно не математики, оперировали только элементарными средствами. Между тем, известное правильное доказательство, как будет ясно из дальнейшего, уже для показателя n = 3 является неэлементарным.
Замечательные продвижения принадлежат Э. Куммеру (1810-1893), который своими исследованиями по проблеме Ферма оказал решающее влияние на развитие алгебраической теории чисел. В XX столетии его методы были усовершенствованы и дополнены (1929 г. и позже) прежде всего благодаря усилиям У. Вандивера, Г. Ламе и Э. Лемера. К 80-м годам XX в. с использованием ЭВМ неразрешимость уравнения хn + yn = zn в натуральных числах была установлена для всех n 2125000 (З. Вагштафф, 1976 г.). Если принять во внимание, что число 2125000 записывается 37628-ю цифрами, то поиски контрпримера к Великой теореме Ферма представлялись совершенно безнадежным занятием.
23 июня 1993 г. математик из Принстона Эндрю Вайлс в докладе на конференции по теории чисел в Кембридже (Великобритания) анонсировал решение проблемы Ю. Таниямы (о модулярности эллиптических кривых с рациональными коэффициентами). Ранее уже было доказано (в 1985 г. Г. Фрей выдвинул гипотезу, которую в 1986 г. доказал К. Рибет), что из доказательства проблемы Таниямы следует утверждение Великой теоремы Ферма. Однако, в начале декабря 1993 г., когда рукопись Э. Вайлса уже готова была отправиться в печать, в его доказательстве были обнаружены пробелы. Автор извинился и попросил два месяца для исправления. Только через год с небольшим появилось полное доказательство гипотезы Таниямы, но уже двух авторов – Э. Вайлса и его ученика Р. Тейлора [6, 7]. Новых пробелов в этих работах специалистами пока не найдено.
Сама по себе Великая теорема Ферма не имеет большого значения для математики. Однако она сыграла важную роль для развития теории алгебраических чисел, теории идеалов, алгебраической геометрии и математики в целом: попытки её доказательства приводили к открытию новых методов, обогативших многие смежные области математики.
Закончим этот параграф следующими элементарными замечаниями о Великой теореме Ферма.
Лемма (об уравнении xn + yn = zn). (1) Если диофантово уравнение xn + yn = zn имеет нетривиальные целочисленные решения, то оно имеет решение в попарно взаимно простых целых числах.
(2) Великую теорему Ферма достаточно доказать для простых нечётных показателей n = p и для n = 4.
Доказательство.
(1) Если xn
+ yn
= zn
для
x,
y,
z
Z
и НОД(x,
y,
z)
= D,
то
![]() ,
т.е.
,
т.е.![]() ,
причём целые числа
,
причём целые числа![]() взаимно просты:НОД(
взаимно просты:НОД(![]() )
= 1. Поэтому
сразу можно считать, что НОД(x,
y,
z)
= 1.
)
= 1. Поэтому
сразу можно считать, что НОД(x,
y,
z)
= 1.
Если какие-то два из чисел x , y , z не взаимно просты, то в их канонических разложениях участвует одно и то же простое число p. Пусть, например, оно участвует в x и z, т.е. x p, y p. Тогда yn = zn – xn p, а значит, y p, вопреки НОД(x, y, z) = 1.
(2) Пусть Великая теорема Ферма доказана для n = 4 и для любого нечётного простого числа n = p. Рассмотрим случай произвольного показателя n.
Если в каноническое разложение n входит нечётное простое число p, т.е. n = pm, то существование нетривиального решения (x; y; z) диофантова уравнения xn + yn = zn равносильно тому, что (xm)p + (ym)p = (zm)p, т.е. существованию нетривиального решения для теоремы Ферма с показателем p – противоречие.
Если же n не делится ни на одно простое нечётное число, то 1 < n = 2k 4, и аналогичные рассуждения показывают, что n = 4m и (xm)4 + (ym)4 = (zm)4, вопреки теореме Ферма для показателя 4.
Лемма доказана.
