Оценки основных характеристик ряда наблюдений

Обычно математическое ожидание и среднее квадратическое отклонение ряда наблюдений неизвестны. В этом случае их приходится оценивать по результатам полученного ряда наблюдений. Если действительное значение искомой величины равно А, то ее оценку обозначают (А с волной).

Оценка математического ожидания ряда наблюдений.

Как следует из теории вероятностей, оценкой математического ожидания ряда наблюдений может служить среднее арифметическое результатов отдельных наблюдений

, (4.1)

где - результаты отдельных наблюдений; n – число наблюдений.

Отклонение между каждым из отдельных значений и средним арифметическим (разности ) называется случайным отклонением результата наблюдения (или остаточной погрешностью) и может иметь как положительный, так и отрицательный знак.

Одним из свойств среднего арифметического является то, что алгебраическая сумма остаточных погрешностей равна нулю. Этим следует пользоваться для контроля правильности подсчета . При неограниченно большом числе наблюдений стремится к математическому ожиданию ряда наблюдений.

Оценка дисперсии ряда наблюдений, согласно теории вероятностей, может быть выражена через остаточные погрешности формулой

.

Оценкой среднего квадратического отклонения ряда наблюдений будет

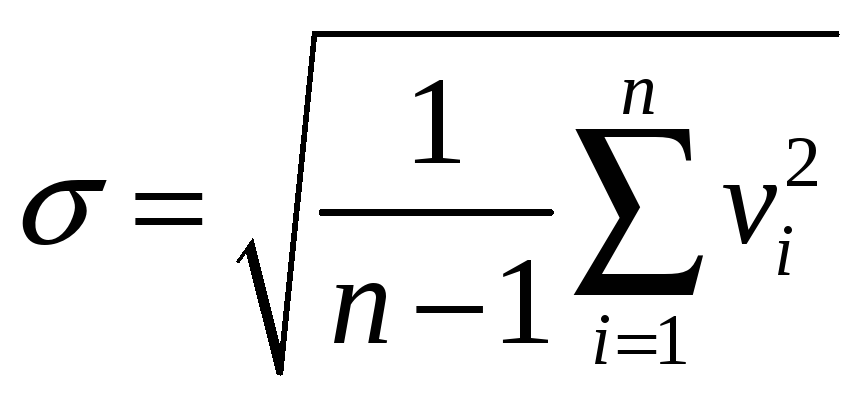. (4.2)

При неограниченно большом числе наблюдений (практически при n>30) оценки и совпадают соответственно с дисперсией и средним квадратическим отклонением ряда наблюдений.

Оценкой среднего квадратического отклонения среднего арифметического будет . Эта величина используется для оценки погрешности результата измерений с многократными наблюдениями.

Рассмотренные оценки результата измерения, выраженные одним числом, называются точечными оценками. Точечная оценка погрешности измерения неполная, поскольку D и указывают на границы интервала, в котором может находиться истинное значение А, но ничего не говорит о вероятности попадания А в этот интервал. Точечная оценка позволяет сделать некоторые выводы о точности проведенных измерений, поэтому рекомендуется ее использовать совместно с другими результатами измерений, а не как окончательный результат.

Интервальные оценки истинного значения

Более полным и надежным способом оценки случайных величин является определение интервальной оценки (а не единичного точечного значения), которая с заданной степенью достоверности включает в себя значение оцениваемого параметра.

При интервальной оценке определяется доверительный интервал, между границами которого с определенной доверительной вероятностью Р находится истинное значение. Если известен закон распределения погрешностей, можно определить вероятность появления погрешности , не выходящей за пределы доверительного интервала. В практике измерений применяют различные значения доверительной вероятности, например, 0.90; 0.95; 0.98; 0.99; 0.9973 и 0.999. Доверительный интервал и доверительную вероятность выбирают в зависимости от конкретных условий измерений. Так, например, при нормальном законе распределения случайных погрешностей со средним квадратическим отклонением s часто пользуются доверительным интервалом от +3s до -3s, для которого доверительная вероятность равна 0.9973. Такая доверительная вероятность означает, что в среднем из 370 случайных погрешностей только одна погрешность по абсолютному значению будет больше 3s. Так как на практике число отдельных измерений редко превышает несколько десятков, появление даже одной случайной погрешности, большей чем 3s, будет маловероятным событием, наличие же двух подобных погрешностей почти невозможно. Это позволяет с достаточным основанием утверждать, что все возможные случайные погрешности измерения, распределенные по нормальному закону, практически не превышают по абсолютному значению 3s (правило «трех сигм»).

Доверительный интервал является одной из основных форм выражения точности измерений. Доверительные границы случайной погрешности , соответствующие доверительной вероятности Р, находят по формуле:

, (4.3)

где t – коэффициент, зависящий от Р и формы закона распределения.

Одну из форм представления результата измерения ГОСТ устанавливает в следующем виде:

А; D от D_Н до D_В; Р,

где А - результат измерения (действительное значение) в единицах измеряемой величины; D, D_Н, D_В – соответственно погрешность измерения с нижней и верхней ее границами в тех же единицах; Р – установленная вероятность, с которой погрешность измерения находится в этих границах. Если границы погрешности симметричны, т.е. , то результат измерения может быть записан так: А.

Обработка результатов измерений

Прямые равноточные измерения с многократными наблюдениями

Результаты многократных наблюдений, получаемые при прямых измерениях величины А, называются равноточными (равнорассеянными), если они являются независимыми, одинаково распределенными случайными величинами. Измерения проводятся одним наблюдателем в одинаковых условиях внешней среды и с помощью одного и того же средства измерения.

Предположим, что при многократном измерении интересующей нас величины получили n отдельных результатов наблюдений. Исключив систематическую погрешность из каждого наблюдения, получаем исправленный ряд значений , математическим ожиданием которого является истинное значение измеряемой величины А. За действительное значение измеряемой величины принимаем среднее арифметическое .

При нормальном законе распределения плотности вероятностей результатов наблюдений и небольшом числе наблюдений среднее арифметическое подчиняется закону распределения Стьюдента с тем же средним арифметическим значением . Особенностью этого распределения является то, что доверительный интервал с уменьшением числа наблюдений расширяется, по сравнению с нормальным законом распределения при той же доверительной вероятности. В формуле (4.3) для оценки доверительных границ случайной погрешности это отражается введением коэффициента вместо t. Коэффициент распределения Стьюдента зависит от числа наблюдений и выбранной доверительной вероятности и находится по таблице (табл. 4.1). Так, при числе наблюдений n = 10 и доверительной вероятности Р = 0.95 = 2.3 (требуемый коэффициент находится на пересечении столбца и строки, соответствующих этим значениям). Зная , результат измерения с доверительной вероятностью Р можно записать в виде

.

Увеличение числа наблюдений позволяет получить более точную оценку истинного значения измеряемой величины.

Т а б л и ц а 4.1. Коэффициенты Стьюдента

n	P
	0.5	0.6	0.7	0.8	0.9	0.95	0.98	0.99	0.999
2	1.00	1.38	2.0	3.1	6.3	12.7	31.8	63.7	636.6
3	0.82	1.06	1.3	1.9	2.9	4.3	7.0	9.9	31.6
4	0.77	0.98	1.3	1.6	2.4	3.2	4.5	5.8	12.9
5	0.74	0.94	1.2	1.5	2.1	2.8	3.7	4.6	8.6
6	0.73	0.92	1.2	1.4	2.0	2.6	3.4	4.0	6.9
7	0.72	0.90	1.2	1.4	1.9	2.4	3.1	3.7	6.0
8	0.71	0.90	1.1	1.4	1.9	2.4	3.0	3.5	5.4
9	0.71	0.90	1.1	1.4	1.9	2.3	2.9	3.4	5.0
10	0.70	0.88	1.1	1.4	1.8	2.3	2.8	3.3	4.8
11	0.69	0.87	1.1	1.3	1.8	2.1	2.6	3.0	4.1
12	0.69	0.86	1.1	1.3	1.7	2.1	2.6	2.9	4.0
20	0.69	0.86	1.1	1.3	1.7	2.1	2.5	2.9	3.9

При обработке результатов измерения с многократными наблюдениями надо учитывать, что результаты наблюдений могут содержать систематическую погрешность, в группе наблюдений могут встречаться грубые погрешности.

Обработка результатов наблюдений производится в следующей последовательности:

1. Исключить известные систематические погрешности из результатов наблюдений (введением поправки).

2. Вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения:

.

3. Вычислить оценку среднего квадратического отклонения результатов наблюдения:

.

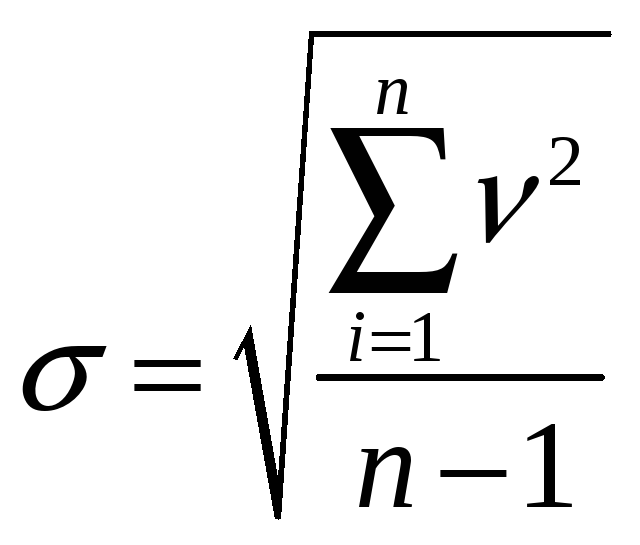Вычислив оценку СКО результата наблюдений, целесообразно проверить наличие в группе наблюдений грубых погрешностей, помня, что при нормальном законе распределения ни одна случайная погрешность , с вероятностью практически равной единице, не может выйти за пределы . Наблюдения, содержащие грубые погрешности, исключают из группы и заново повторяют вычисления и .

4. Вычислить оценку СКО результата измерения

.

5. Вычислить доверительные границы Δ случайной погрешности результата измерения при заданной вероятности Р

,

где - коэффициент Стьюдента.

6. Записать результат измерения в регламентированной стандартом форме:

.

При записи чисел и Δ используются следующие правила округления результатов и погрешностей измерений:

1) Число, выражающее результат измерения , должно оканчиваться цифрой того же разряда, что и предельное значение погрешности измерения Δ. При этом лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются. Например, число 1123 (любых единиц измерения) при погрешности измерения (тех же единиц) округляют до 1120, а число 1.123 при погрешности - до 1.12.

Если десятичная дробь оканчивается нулями, то соответственно отбрасываются не все нули. Например, для числа 1.1 при той же погрешности 0.05 следует записать 1.10.

2) Если первая из заменяемых нулями или отбрасываемых цифр в числе, выражающем , меньше 5, то остающиеся цифры не изменяют; если она больше или равна 5, то последнюю оставшуюся цифру увеличивают на единицу.

3) Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или нули, то последнюю сохраняемую цифру не изменяют, если она четная и увеличивают, если она нечетная. Например, число 22.5 при сохранении двух значащих цифр округляют до 22, а число 23.5 – до 24.

4) Число, выражающее предельное значение погрешности измерения, должно содержать не более двух цифр.