
Математика для юристов - Д.А. Ловцова
.pdf3.ɉɨɥɨɠɢɬɶ ɇɈȾ ɪɚɜɧɵɦ X ɢ ɩɟɪɟɣɬɢ ɤ ɩ.6.
4.ɉɨɥɨɠɢɬɶ X ɪɚɜɧɵɦ X Y ɢ ɩɟɪɟɣɬɢ ɤ ɩ.1.
5.ɉɨɥɨɠɢɬɶ Y ɪɚɜɧɵɦ Y X ɢ ɩɟɪɟɣɬɢ ɤ ɩ.1.
6.Ɂɚɤɨɧɱɢɬɶ ɜɵɱɢɫɥɟɧɢɹ (ɋɌɈɉ).
|
|
Ɍɚɛɥɢɰɚ 3.3 |
|
ɉɭɧɤɬ |
Ɋɟɡɭɥɶɬɚɬ |
ɒɚɝ |
ɚɥɝɨ- |
ɞɟɣɫɬɜɢɹ |
|
ɪɢɬɦɚ |
|
0 |
0 |
X 12, Y 18. |
1 |
1 |
X!Y? – ɇɟɬ. |
2 |
2 |
X Y? – Ⱦɚ. |
3 |
5 |
Y Y X 6. |
4 |
1 |
X!Y? – Ⱦɚ. |
5 |
4 |
X X Y 6. |
6 |
1 |
X!Y? – ɇɟɬ. |
7 |
2 |
X Y? – ɇɟɬ. |
8 |
3 |
ɇɈȾ 6. |
9 |
6 |
ɋɌɈɉ. |
ɉɪɨɜɟɪɢɦ ɪɚɛɨɬɭ ɷɬɨɝɨ ɚɥɝɨɪɢɬɦɚ ɧɚ ɩɪɢɦɟɪɟ. ɉɭɫɬɶ A 12 ɢ B 18. ɇɚɲɢ
ɞɟɣɫɬɜɢɹ ɩɨ ɪɟɚɥɢɡɚɰɢɢ ɚɥɝɨɪɢɬɦɚ ɫɜɟɞɟɦ ɜ ɬɚɛɥ.3.3. Ʉɚɤ ɜɢɞɢɦ, ɩɪɨɰɟɞɭɪɚ
ɜɵɱɢɫɥɟɧɢɣ, ɩɨɪɨɠɞɚɟɦɚɹ ɚɥɝɨɪɢɬɦɨɦ, ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɸ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɫɬɶ ɲɚɝɨɜ. ɇɚ ɤɚɠɞɨɦ ɲɚɝɟ ɜɵɩɨɥɧɹɟɬɫɹ ɬɨɬ ɢɥɢ ɢɧɨɣ ɩɭɧɤɬ ɢɡ ɨɩɢɫɚɧɢɹ ɚɥɝɨɪɢɬɦɚ.
ɇɚɡɨɜɟɦ ɨɫɧɨɜɧɵɟ ɬɪɟɛɨɜɚɧɢɹ, ɤɨɬɨɪɵɦ ɞɨɥɠɧɵ ɨɬɜɟɱɚɬɶ ɚɥɝɨɪɢɬɦɵ, ɟɫɥɢ ɢɯ ɪɟɚɥɢɡɚɰɢɸ ɩɪɟɞɩɨɥɚɝɚɟɬɫɹ ɜɵɩɨɥɧɹɬɶ ɧɚ ɤɨɦɩɶɸɬɟɪɟ.
1. Ʉɨɧɟɱɧɨɫɬɶ. ɗɬɨ ɬɪɟɛɨɜɚɧɢɟ ɫɨɫɬɨɢɬ ɜ ɬɨɦ, ɱɬɨ ɡɚɩɭɳɟɧɧɵɣ ɜ ɪɚɛɨɬɭ ɚɥɝɨɪɢɬɦ ɡɚ ɤɨɧɟɱɧɨɟ ɱɢɫɥɨ ɲɚɝɨɜ ɞɨɥɠɟɧ ɡɚɜɟɪɲɢɬɶɫɹ ɩɨɥɭɱɟɧɢɟɦ ɢɫɤɨɦɨɝɨ ɪɟɡɭɥɶɬɚɬɚ.
2. Ɉɩɪɟɞɟɥɟɧɧɨɫɬɶ. ɇɚ ɥɸɛɨɦ ɲɚɝɟ ɜɵɱɢɫɥɟɧɢɣ ɞɨɥɠɧɨ ɛɵɬɶ ɹɫɧɨ, ɱɬɨ ɞɟɥɚɬɶ ɞɚɥɶɲɟ (ɩɟɪɟɣɬɢ ɤ ɫɥɟɞɭɸɳɟɦɭ ɩɭɧɤɬɭ, ɜɟɪɧɭɬɶɫɹ ɤ ɬɨɦɭ ɢɥɢ ɢɧɨɦɭ ɢɡ ɩɪɟɞɵɞɭɳɢɯ ɩɭɧɤɬɨɜ ɢɥɢ ɡɚɤɨɧɱɢɬɶ ɪɚɛɨɬɭ).
3. Ʉɚɠɞɨɦɭ ɚɥɝɨɪɢɬɦɭ ɫɬɚɜɢɬɫɹ ɜ ɫɨɨɬɜɟɬɫɬɜɢɟ ɦɧɨɠɟɫɬɜɨ ɱɢɫɥɨɜɵɯ ɜɟɥɢɱɢɧ, ɞɨɩɭɫɬɢɦɵɯ ɞɥɹ ɧɟɝɨ ɜ ɤɚɱɟɫɬɜɟ ɢɫɯɨɞɧɵɯ ɞɚɧɧɵɯ. Ɍɨɱɧɨ ɬɚɤ ɨɩɪɟɞɟɥɟɧɨ ɢ ɦɧɨɠɟɫɬɜɨ ɞɨɩɭɫɬɢɦɵɯ ɞɥɹ ɷɬɨɝɨ ɚɥɝɨɪɢɬɦɚ ɪɟɡɭɥɶɬɚɬɨɜ ɜɵɱɢɫɥɟɧɢɣ. ɋɤɚɠɟɦ, ɞɥɹ ɚɥɝɨɪɢɬɦɚ ȿɜɤɥɢɞɚ ɢɫɯɨɞɧɵɟ ɜɟɥɢɱɢɧɵ Ⱥ ɢ ȼ, ɪɟɡɭɥɶɬɚɬ ɟɝɨ ɪɚɛɨɬɵ ɇɈȾ ɨɬɧɨɫɹɬɫɹ ɤ ɤɥɚɫɫɭ ɧɚɬɭɪɚɥɶɧɵɯ ɱɢɫɟɥ. ɉɪɢɦɟɧɟɧɢɟ ɚɥɝɨɪɢɬɦɚ ɤ ɜɟɥɢɱɢɧɚɦ, ɤɨɬɨɪɵɟ ɧɟ ɹɜɥɹɸɬɫɹ ɞɥɹ ɧɟɝɨ ɞɨɩɭɫɬɢɦɵɦɢ, ɱɪɟɜɚɬɨ, ɤɚɤ ɦɢɧɢɦɭɦ, ɩɨɥɭɱɟɧɢɟɦ ɚɛɫɭɪɞɧɵɯ ɪɟɡɭɥɶɬɚɬɨɜ, ɧɨ, ɫɤɨɪɟɟ ɜɫɟɝɨ, ɚɥɝɨɪɢɬɦ ɧɚ ɷɬɢɯ ɞɚɧɧɵɯ ɧɟ ɛɭɞɟɬ ɨɬɜɟɱɚɬɶ ɬɪɟɛɨɜɚɧɢɹɦ ɤɨɧɟɱɧɨɫɬɢ ɢ ɨɩɪɟɞɟɥɟɧɧɨɫɬɢ. ȼ ɷɬɨɦ ɭɛɟɠɞɚɟɬ ɩɪɢɦɟɧɟɧɢɟ ɚɥɝɨɪɢɬɦɚ ȿɜɤɥɢɞɚ ɤ ɨɬɪɢɰɚɬɟɥɶɧɵɦ ɰɟɥɵɦ ɱɢɫɥɚɦ.
Ɋɚɫɫɦɨɬɪɢɦ ɫɩɨɫɨɛɵ ɡɚɞɚɧɢɹ ɚɥɝɨɪɢɬɦɨɜ. Ⱥɥɝɨɪɢɬɦ ȿɜɤɥɢɞɚ ɛɵɥ ɡɚɞɚɧ ɫɜɨɢɦ ɫɥɨɜɟɫɧɵɦ (ɜɟɪɛɚɥɶɧɵɦ) ɨɩɢɫɚɧɢɟɦ. əɫɧɨ, ɱɬɨ ɬɚɤ ɦɨɠɧɨ ɨɩɢɫɚɬɶ ɪɟɲɟɧɢɟ ɫɪɚɜɧɢɬɟɥɶɧɨ ɩɪɨɫɬɨɣ ɡɚɞɚɱɢ. Ȼɨɥɟɟ ɢɥɢ ɦɟɧɟɟ ɫɥɨɠɧɚɹ ɡɚɞɚɱɚ ɩɨɬɪɟɛɭɟɬ ɝɪɨɦɨɡɞɤɨɝɨ, ɡɚɩɭɬɚɧɧɨɝɨ ɫɥɨɜɟɫɧɨɝɨ ɨɩɢɫɚɧɢɹ. ɂ ɜɫɟ ɪɚɜɧɨ, ɜ ɫɚɦɨɦ ɩɨɞɪɨɛɧɨɦ ɬɚɤɨɦ ɨɩɢɫɚɧɢɢ ɦɧɨɝɨɟ ɨɫɬɚɧɟɬɫɹ ɦɟɠɞɭ ɫɬɪɨɤ, ɜ ɤɨɧɬɟɤɫɬɟ. ɇɚɩɪɢɦɟɪ, ɜ ɚɥɝɨɪɢɬɦɟ
41
ȿɜɤɥɢɞɚ ɦɵ ɧɟ ɭɤɚɡɚɥɢ ɹɜɧɨ, ɱɬɨ ɩɨɫɥɟ ɩɭɧɤɬɚ 0 ɞɨɥɠɟɧ ɜɵɩɨɥɧɹɬɶɫɹ ɩɭɧɤɬ 1, ɚ ɩɪɢ ɧɟɜɵɩɨɥɧɟɧɢɢ ɭɫɥɨɜɢɹ X ɛɨɥɶɲɟ Y ɜ ɩɭɧɤɬɟ 1 ɫɥɟɞɭɟɬ ɩɟɪɟɣɬɢ ɤ ɩɭɧɤɬɭ 2. ȼɫɟ ɷɬɨ – ɧɚɪɭɲɟɧɢɟ ɬɪɟɛɨɜɚɧɢɹ ɨɩɪɟɞɟɥɟɧɧɨɫɬɢ ɚɥɝɨɪɢɬɦɚ. ȼ ɟɫɬɟɫɬɜɟɧɧɨɦ ɹɡɵɤɟ ɢɦɟɸɬɫɹ ɫɢɧɨɧɢɦɵ, ɚ ɟɫɬɶ ɢ ɦɧɨɝɨɡɧɚɱɧɵɟ ɫɥɨɜɚ. ɉɨɷɬɨɦɭ ɩɨɥɭɱɢɬɶ ɫɬɪɨɝɨɟ ɡɚɞɚɧɢɟ ɚɥɝɨɪɢɬɦɚ ɫɪɟɞɫɬɜɚɦɢ ɟɫɬɟɫɬɜɟɧɧɨɝɨ ɹɡɵɤɚ ɧɟɥɶɡɹ.
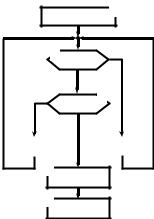
ɋɜɨɛɨɞɟɧ ɨɬ ɭɤɚɡɚɧɧɵɯ ɧɟɞɨɫɬɚɬɤɨɜ ɫɚɦɵɣ ɧɚɝɥɹɞɧɵɣ ɫɩɨɫɨɛ ɡɚɞɚɧɢɹ ɚɥɝɨɪɢɬ-
ɦɚ – ɝɪɚɮɢɱɟɫɤɢɣ, ɚ ɢɦɟɧɧɨ, ɩɪɟɞɫɬɚɜɥɟɧɢɟ ɟɝɨ ɜ ɮɨɪɦɟ ɝɪɚɮɚ. Ɍɚɤ, ɧɚ ɪɢɫ.3.3 ɩɨɤɚ-
ɡɚɧ ɝɪɚɮ ɚɥɝɨɪɢɬɦɚ ɜɵɱɢɫɥɟɧɢɹ ɇɈȾ ɩɨ ȿɜɤɥɢɞɭ. ɋɪɚɜɧɢɜ ɪɢɫ.3.3 ɫ ɜɟɪɛɚɥɶɧɵɦ ɨɩɢɫɚɧɢɟɦ ɷɬɨɝɨ ɚɥɝɨɪɢɬɦɚ, ɥɟɝɤɨ ɭɛɟɞɢɬɶɫɹ ɜ ɬɨɦ, ɱɬɨ ɨɧɢ ɩɪɚɤɬɢɱɟɫɤɢ ɢɞɟɧɬɢɱɧɵ. Ɉɬɦɟɬɢɦ, ɤɫɬɚɬɢ, ɱɬɨ ɬɚɤɨɟ ɭɤɚɡɚɧɢɟ ɜɟɪɛɚɥɶɧɨɝɨ ɚɥɝɨɪɢɬɦɚ ɤɚɤ «ɉɨɥɨɠɢɬɶ X X Y!» ɧɚ ɝɪɚɮɟ ɡɚɞɚɟɬɫɹ ɤɨɧɫɬɪɭɤɰɢɟɣ: X: X Y, ɤɨɬɨɪɭɸ ɧɚɡɵɜɚɸɬ ɨɩɟɪɚɬɨɪɨɦ ɩɪɢɫɜɚɢɜɚɧɢɹ.
Ɉɩɢɲɟɦ ɩɨɞɪɨɛɧɟɟ ɫɪɟɞɫɬɜɚ ɝɪɚɮɢɱɟɫɤɨɝɨ ɩɪɟɞɫɬɚɜɥɟɧɢɹ ɚɥɝɨɪɢɬɦɨɜ.
X:=A; Y:=B0
1 X!Y 1
0
1X Y 2 0
5 |
|
|
|
|
|
4 |
|
Y:=Y X |
|
X:=X Y |
|
||
|
|
|
|
|||
|
|
3 ɇɈȾ:=X
6
ɇɚ ɬɨɦ ɢɥɢ ɢɧɨɦ ɲɚɝɟ ɜɵɱɢɫɥɟɧɢɣ ɤɨɦɩɶɸɬɟɪ ɜɵɩɨɥɧɹɟɬ ɞɟɣɫɬɜɢɹ ɞɜɭɯ ɬɢɩɨɜ. ɉɟɪɜɵɣ ɬɢɩ ɞɟɣɫɬɜɢɣ – ɫɨɞɟɪ-
ɠɚɬɟɥɶɧɚɹ ɨɛɪɚɛɨɬɤɚ ɢɧɮɨɪɦɚɰɢɢ (ɜɜɨɞ ɢɫɯɨɞɧɵɯ ɞɚɧɧɵɯ, ɜɵɱɢɫɥɟɧɢɟ ɡɧɚɱɟɧɢɹ ɩɟɪɟɦɟɧɧɨɣ, ɧɚɩɪɢɦɟɪ, Y:=Y X, ɜɵɜɨɞ ɪɟɡɭɥɶɬɚɬɨɜ ɜɵɱɢɫɥɟɧɢɣ ɢ ɬ.ɩ.). ȼɬɨɪɨɣ ɬɢɩ ɞɟɣɫɬɜɢɣ – ɚɧɚɥɢɡ ɪɟɡɭɥɶɬɚɬɨɜ, ɩɨɥɭɱɟɧɧɵɯ ɧɚ ɩɪɟɞɵɞɭɳɢɯ ɲɚɝɚɯ, ɢ ɜɵɛɨɪ ɞɚɥɶɧɟɣɲɟɝɨ ɩɭɬɢ ɪɚɡɜɢɬɢɹ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɩɪɨɰɟɫɫɚ (ɫɤɚɠɟɦ, ɩɪɨɜɟɪɤɚ ɭɫɥɨɜɢɹ X!Y ɢ ɩɟɪɟɯɨɞ ɩɨ ɪɟɡɭɥɶɬɚɬɭ ɩɪɨɜɟɪɤɢ ɧɚ ɬɨɬ ɢɥɢ ɢɧɨɣ ɩɭɧɤɬ ɚɥɝɨɪɢɬɦɚ). ȼ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɷɬɢɦ, ɞɥɹ ɝɪɚɮɢɱɟɫɤɨɝɨ ɩɪɟɞɫɬɚɜɥɟɧɢɹ ɚɥɝɨɪɢɬɦɨɜ ɢɫɩɨɥɶɡɭɟɦ ɞɜɚ ɫɢɦɜɨɥɚ:
9ɩɪɹɦɨɭɝɨɥɶɧɢɤ, ɜɧɭɬɪɢ ɤɨɬɨɪɨɝɨ ɡɚɩɢɫɵɜɚɟɬɫɹ ɞɟɣɫɬɜɢɟ ɩɟɪɜɨɝɨ ɬɢɩɚ, ɜɵɩɨɥɧɹɟɦɨɟ ɧɚ ɞɚɧɧɨɦ ɲɚɝɟ ɜɵɱɢɫɥɟɧɢɣ,
9ɪɨɦɛ (ɢɥɢ ɲɟɫɬɢɭɝɨɥɶɧɢɤ, ɩɨɥɭɱɟɧɧɵɣ ɭɫɟɱɟɧɢɟɦ ɪɨɦɛɚ, ɤɚɤ ɧɚ ɪɢɫ.3.3), ɜɧɭɬɪɢ ɤɨɬɨɪɨɝɨ ɡɚɩɢɫɵɜɚɟɬɫɹ ɩɪɨɜɟɪɹɟɦɨɟ ɭɫɥɨɜɢɟ.
ɗɬɢ ɫɢɦɜɨɥɵ ɧɚɡɵɜɚɸɬ ɜɟɪɲɢɧɚɦɢ ɝɪɚɮɚ: ɩɪɹɦɨɭɝɨɥɶɧɢɤ – ɨɩɟɪɚɬɨɪɧɨɣ ɜɟɪɲɢɧɨɣ, ɚ ɪɨɦɛ (ɲɟɫɬɢɭɝɨɥɶɧɢɤ) – ɭɫɥɨɜɧɨɣ ɜɟɪɲɢɧɨɣ.
ȼɟɪɲɢɧɵ ɝɪɚɮɚ ɫɨɟɞɢɧɹɸɬ ɞɭɝɚɦɢ (ɫɬɪɟɥɤɚɦɢ) ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ
ɫɥɨɝɢɤɨɣ ɪɚɡɜɢɬɢɹ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɩɪɨɰɟɫɫɚ.
42
Ɉɩɟɪɚɬɨɪɧɚɹ ɜɟɪɲɢɧɚ ɦɨɠɟɬ ɢɦɟɬɶ ɨɞɢɧ ɢɥɢ ɧɟɫɤɨɥɶɤɨ ɜɯɨɞɨɜ (ɤ ɧɟɣ ɩɨɞɯɨɞɹɬ ɨɞɧɚ ɢɥɢ ɧɟɫɤɨɥɶɤɨ ɫɬɪɟɥɨɤ), ɧɨ ɭ ɧɟɟ ɞɨɥɠɟɧ ɛɵɬɶ ɨɞɢɧ ɢ ɬɨɥɶɤɨ ɨɞɢɧ ɜɵɯɨɞ (ɢɡ ɧɟɟ ɜɵɯɨɞɢɬ ɥɢɲɶ ɨɞɧɚ ɫɬɪɟɥɤɚ).
ɍɫɥɨɜɧɚɹ ɜɟɪɲɢɧɚ, ɤɚɤ ɢ ɨɩɟɪɚɬɨɪɧɚɹ, ɦɨɠɟɬ ɢɦɟɬɶ ɨɞɢɧ ɢɥɢ ɧɟɫɤɨɥɶɤɨ ɜɯɨɞɨɜ. ɉɪɨɜɟɪɹɟɦɨɟ ɭɫɥɨɜɢɟ ɜ ɦɨɦɟɧɬ ɟɝɨ ɩɪɨɜɟɪɤɢ ɦɨɠɟɬ ɜɵɩɨɥɧɹɬɶɫɹ, ɚ ɦɨɠɟɬ ɢ ɧɟ ɜɵɩɨɥɧɹɬɶɫɹ. ɉɨɷɬɨɦɭ ɭɫɥɨɜɧɚɹ ɜɟɪɲɢɧɚ ɢɦɟɟɬ ɞɜɚ ɜɵɯɨɞɚ. Ɉɞɢɧ ɢɡ ɧɢɯ ɨɬɜɟɱɚɟɬ ɬɨɦɭ ɧɚɩɪɚɜɥɟɧɢɸ ɯɨɞɚ ɜɵɱɢɫɥɟɧɢɣ, ɤɨɬɨɪɨɟ ɢɦɟɟɬ ɦɟɫɬɨ ɩɪɢ ɜɵɩɨɥɧɟɧɢɢ ɭɫɥɨɜɢɹ. ɗɬɨɬ ɜɵɯɨɞ ɨɬɦɟɱɚɟɬɫɹ ɫɢɦɜɨɥɨɦ 1 (ɢɫɬɢɧɚ). ȼɬɨɪɨɣ ɜɵɯɨɞ ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɬɨɦɭ ɧɚɩɪɚɜɥɟɧɢɸ ɪɚɡɜɢɬɢɹ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɩɪɨɰɟɫɫɚ, ɤɨɬɨɪɨɟ ɢɦɟɟɬ ɦɟɫɬɨ, ɤɨɝɞɚ ɭɫɥɨɜɢɟ ɜ ɪɨɦɛɟ ɧɟ ɜɵɩɨɥɧɹɟɬɫɹ. ɗɬɨɬ ɜɵɯɨɞ ɨɬɦɟɱɚɟɬɫɹ ɫɢɦɜɨɥɨɦ 0 (ɥɨɠɶ).
ɋɪɟɞɢ ɨɩɟɪɚɬɨɪɧɵɯ ɜɟɪɲɢɧ ɞɜɟ – ɨɫɨɛɵɟ: ɧɚɱɚɥɶɧɚɹ ɢ ɤɨɧɟɱɧɚɹ. ɇɚɱɚɥɶɧɚɹ ɜɟɪɲɢɧɚ ɧɟ ɢɦɟɟɬ ɜɯɨɞɨɜ, ɤɨɧɟɱɧɚɹ ɜɟɪɲɢɧɚ ɧɟ ɢɦɟɟɬ ɜɵɯɨɞɚ. ɇɚ ɪɢɫ. 3.3. ɧɚɱɚɥɶɧɚɹ ɜɟɪɲɢɧɚ – ȼɜɨɞ X,Y, ɚ ɤɨɧɟɱɧɚɹ – ȼɵɜɨɞ ɇɈȾ.
Ʉɨɪɪɟɤɬɧɨ ɪɚɡɪɚɛɨɬɚɧɧɵɣ ɝɪɚɮ (ɬɨɬ, ɤɨɬɨɪɵɣ ɨɬɜɟɱɚɟɬ ɬɪɟɛɨɜɚɧɢɹɦ ɤɨɧɟɱɧɨɫɬɢ ɢ ɨɩɪɟɞɟɥɟɧɧɨɫɬɢ) ɨɬɥɢɱɚɟɬɫɹ ɬɟɦ, ɱɬɨ:
9ɨɧ ɞɨɥɠɟɧ ɢɦɟɬɶ ɨɞɧɭ ɢ ɬɨɥɶɤɨ ɨɞɧɭ ɧɚɱɚɥɶɧɭɸ ɜɟɪɲɢɧɭ, ɨɞɧɭ ɢ ɬɨɥɶɤɨ ɨɞɧɭ ɤɨɧɟɱɧɭɸ ɜɟɪɲɢɧɭ,
9ɢɡ ɥɸɛɨɣ ɜɟɪɲɢɧɵ ɝɪɚɮɚ ɞɨɥɠɟɧ ɛɵɬɶ ɩɭɬɶ ɜ ɤɨɧɟɱɧɭɸ ɜɟɪɲɢɧɭ.
Ⱦɥɹ ɬɨɝɨ ɱɬɨɛɵ ɜ ɩɨɹɫɧɹɸɳɟɦ ɬɟɤɫɬɟ ɦɨɠɧɨ ɛɵɥɨ ɫɨɫɥɚɬɶɫɹ ɧɚ ɬɭ ɢɥɢ ɢɧɭɸ ɜɟɪɲɢɧɭ ɝɪɚɮɚ, ɟɟ ɫɧɚɛɠɚɸɬ ɦɟɬɤɨɣ. Ɉɛɵɱɧɨ ɜ ɤɚɱɟɫɬɜɟ ɦɟɬɤɢ ɢɫɩɨɥɶɡɭɸɬ ɱɢɫɥɨ, ɡɚɩɢɫɵɜɚɟɦɨɟ ɜ ɪɚɡɪɵɜ ɤɨɧɬɭɪɚ ɜɟɪɲɢɧɵ. ɇɚ ɪɢɫ. 3.3 ɜɟɪɲɢɧɵ ɝɪɚɮɚ ɨɬɦɟɱɟɧɵ ɫɢɦɜɨɥɚɦɢ, ɤɨɬɨɪɵɟ ɨɬɜɟɱɚɸɬ ɩɭɧɤɬɚɦ ɫɥɨɜɟɫɧɨɝɨ ɚɥɝɨɪɢɬɦɚ ȿɜɤɥɢɞɚ.
Вопросы и задачи для самоконтроля
1.Ɉɩɪɟɞɟɥɢɬɶ ɩɨɧɹɬɢɟ «ɩɨɡɢɰɢɨɧɧɚɹ ɫɢɫɬɟɦɚ ɫɱɢɫɥɟɧɢɹ».
2.ȼɵɩɨɥɧɢɬɶ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɵɣ ɩɟɪɟɜɨɞ ɢɡ ɞɟɫɹɬɢɱɧɨɣ ɫɢɫɬɟɦɵ ɫɱɢɫɥɟɧɢɹ ɜ ɞɜɨɢɱɧɭɸ, ɚ ɢɡ ɧɟɟ ɜ ɲɟɫɬɧɚɞɰɚɬɟɪɢɱɧɭɸ, ɩɨɫɥɟ ɱɟɝɨ ɜɟɪɧɭɬɶɫɹɜɞɟɫɹɬɢɱɧɭɸɞɥɹɱɢɫɟɥ:
130, 251, 617, 976, 1920, 5295, 12908.
3.ɋ ɤɚɤɢɦɢ ɤɥɚɫɫɚɦɢ ɱɢɫɟɥ ɨɩɟɪɢɪɭɸɬ ɧɚ ɩɪɚɤɬɢɤɟ ɢ ɜ ɦɚɬɟɦɚɬɢɤɟ? Ⱦɚɬɶ ɯɚɪɚɤɬɟɪɢɫɬɢɤɭ ɤɚɠɞɨɦɭ ɢɡ ɤɥɚɫɫɨɜ ɱɢɫɟɥ ɢ ɨɬɧɨɲɟɧɢɹɦ ɦɟɠɞɭ ɤɥɚɫɫɚɦɢ.
4.ɉɨɹɫɧɢɬɶ ɫɦɵɫɥ ɨɩɟɪɚɰɢɢ (A)mod M. ɇɚɣɬɢ (A)mod M ɞɥɹ
A {1000, 73,7} ɢ M {19, 10, 6}.
43
5. ɋɮɨɪɦɭɥɢɪɨɜɚɬɶ ɚɥɝɨɪɢɬɦ ɨɤɪɭɝɥɟɧɢɹ ɞɟɫɹɬɢɱɧɵɯ ɞɪɨɛɟɣ. Ɉɤɪɭɝɥɢɬɶ ɱɢɫɥɨ
S 3.14159265358979323846264338327950
ɞɨ ɲɟɫɬɢ, ɞɨ ɞɜɭɯ ɡɧɚɤɨɜ, ɞɨ ɰɟɥɨ-
ɝɨ. |
|
|
Ɍɚɛɥɢɰɚ Ȼɘ |
|
6. ɉɪɟɞɫɬɚɜɢɬɶ ɜ ɫɬɚɧɞɚɪɬɧɨɣ |
ɝɨɪɨɞ |
ɩɨ ɲɬɚɬɭ |
ɧɟɤɨɦɩɥɟɤɬ |
|
ɮɨɪɦɟ ɱɢɫɥɚ |
Ȼɪɸɤɨɜɨ |
145 |
|
55 |
0.000765402, 76540.2 |
ɘɛɤɢɧɨ |
352 |
|
98 |
|
|
|
|
|
7.Ⱦɚɧɧɵɟ ɨ ɤɨɥɢɱɟɫɬɜɟ ɫɭɞɟɣ ɜ ɝɨɪɨɞɚɯ Ȼɪɸɤɨɜɨ ɢ ɘɛɤɢɧɨ ɫɜɟɞɟɧɵ ɜ ɬɚɛɥ. Ȼɘ. ȼ ɤɚɤɨɦ ɢɡ ɝɨɪɨɞɨɜ ɫɢɬɭɚɰɢɹ ɫ ɫɭɞɶɹɦɢ ɫɥɨɠɧɟɟ?
8.Ɋɚɡɪɚɛɨɬɚɬɶ ɝɪɚɮ ɚɥɝɨɪɢɬɦɚ ɨɤɪɭɝɥɟɧɢɹ ɩɪɚɜɢɥɶɧɨɣ ɞɪɨɛɢ ɞɨ k ɪɚɡɪɹɞɨɜ ɩɨɫɥɟ ɬɨɱɤɢ.
Глава 4. Функции
4.1. Понятие функции
ɉɭɫɬɶ X ɢ Y – ɧɟɩɭɫɬɵɟ ɱɢɫɥɨɜɵɟ ɦɧɨɠɟɫɬ-
ɜɚ (ɪɢɫ.4.1).
Ɏɭɧɤɰɢɟɣ ɢɡ X ɜ Y ɧɚɡɵɜɚɸɬ ɡɚɤɨɧ f, ɩɨ ɤɨɬɨɪɨɦɭ ɤɚɠɞɨɦɭ ɷɥɟɦɟɧɬɭ x X ɫɬɚɜɢɬɫɹ ɜ ɫɨɨɬɜɟɬɫɬɜɢɟ ɟɞɢɧɫɬɜɟɧɧɵɣ ɷɥɟɦɟɧɬ y Y.
X Y
y x
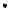
ɗɥɟɦɟɧɬ x X ɧɚɡɵɜɚɸɬ ɚɪɝɭɦɟɧɬɨɦ, ɚ ɷɥɟɦɟɧɬ y Y – ɡɧɚɱɟɧɢɟɦ ɮɭɧɤɰɢɢ f. Ɇɧɨɠɟ-
ɫɬɜɨ X ɧɚɡɵɜɚɟɬɫɹ ɨɛɥɚɫɬɶɸ ɨɩɪɟɞɟɥɟɧɢɹ ɮɭɧɤɰɢɢ f (ɨɛɥɚɫɬɶɸ ɟɟ ɫɭɳɟɫɬɜɨɜɚɧɢɹ), ɚ ɦɧɨɠɟɫɬɜɨ Y – ɨɛɥɚɫɬɶɸ ɡɧɚɱɟɧɢɣ ɮɭɧɤɰɢɢ f. Ɉɛɥɚɫɬɶ ɨɩɪɟɞɟɥɟɧɢɹ ɢ ɨɛɥɚɫɬɶ ɡɧɚɱɟɧɢɣ ɮɭɧɤɰɢɢ f ɨɛɨɡɧɚɱɢɦ ɤɚɤ Df ɢ Ef, ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ.
Ɂɚɞɚɬɶ ɮɭɧɤɰɢɸ – ɡɧɚɱɢɬ ɭɤɚɡɚɬɶ ɨɛɥɚɫɬɶ ɟɟ ɨɩɪɟɞɟɥɟɧɢɹ, ɨɛɥɚɫɬɶ ɟɟ ɡɧɚɱɟɧɢɣ ɢ ɫɮɨɪɦɭɥɢɪɨɜɚɬɶ ɡɚɤɨɧ (ɩɪɚɜɢɥɨ) ɨ ɬɨɦ, ɤɚɤ ɞɥɹ ɤɚɠɞɨɝɨ ɢɡ ɡɚɞɚɧɧɵɯ x ɩɨɥɭɱɚɸɬ ɫɜɨɣ y.
ɂɡɜɟɫɬɧɵ ɫɥɟɞɭɸɳɢɟ ɫɩɨɫɨɛɵ ɡɚɞɚɧɢɹ ɮɭɧɤɰɢɣ:
9ɚɧɚɥɢɬɢɱɟɫɤɢɣ,
9ɬɚɛɥɢɱɧɵɣ,
9ɝɪɚɮɢɱɟɫɤɢɣ.
Ɂɚɞɚɬɶ ɮɭɧɤɰɢɸ ɚɧɚɥɢɬɢɱɟɫɤɢ – ɷɬɨ ɡɚɩɢɫɚɬɶ ɟɟ ɮɨɪɦɭɥɨɣ. ȿɫɥɢ ɦɧɨɠɟɫɬɜɚ X ɢ Y ɨɩɪɟɞɟɥɟɧɵ, ɬɨ ɮɭɧɤɰɢɸ ɢɡ X ɜ Y ɡɚɞɚɸɬ ɡɚɩɢ-
44
ɫɶɸ ɜɢɞɚ y f(x). ɗɬɨ ɧɚɢɛɨɥɟɟ ɤɨɦɩɚɤɬɧɵɣ, ɭɞɨɛɧɵɣ ɢ ɭɧɢɜɟɪɫɚɥɶɧɵɣ ɫɩɨɫɨɛ ɡɚɞɚɧɢɹ ɮɭɧɤɰɢɢ. Ɏɨɪɦɭɥɨɣ ɡɚɞɚɸɬ ɧɚɛɨɪ ɜɵɱɢɫɥɢɬɟɥɶɧɵɯ ɨɩɟɪɚɰɢɣ ɧɚɞ x, ɜɵɩɨɥɧɢɜ ɤɨɬɨɪɵɟ ɩɨɥɭɱɚɸɬ y. Ɉɛɵɱɧɨ ɩɨ ɮɨɪɦɭɥɟ ɦɨɠɧɨ ɧɚɣɬɢ ɢ ɨɛɥɚɫɬɶ ɨɩɪɟɞɟɥɟɧɢɹ ɮɭɧɤɰɢɢ, ɢ ɨɛɥɚɫɬɶ ɟɟ ɡɧɚɱɟɧɢɣ. Ʉɨɝɞɚ ɦɵ ɱɢɬɚɟɦ ɡɚɩɢɫɶ
y 0.25ux3, |
(4.1) |
ɧɚɦ ɹɫɧɨ, ɱɬɨ ɷɬɚ ɮɭɧɤɰɢɹ ɫɬɚɜɢɬ ɜ ɫɨɨɬɜɟɬɫɬɜɢɟ ɤɚɠɞɨɦɭ ɱɢɫɥɭ x ɱɟɬɜɟɪɬɭɸ ɱɚɫɬɶ ɟɝɨ ɤɭɛɚ. ɗɬɚ ɮɭɧɤɰɢɹ ɨɩɪɟɞɟɥɟɧɚ ɧɚ ɜɫɟɣ ɱɢɫɥɨɜɨɣ ɨɫɢ: x R, ɢ ɨɛɥɚɫɬɶ ɟɟ ɡɧɚɱɟɧɢɣ – ɬɨɠɟ ɦɧɨɠɟɫɬɜɨ ɜɟɳɟɫɬɜɟɧɧɵɯ ɱɢɫɟɥ y R.
Ʉɨɧɟɱɧɨ, ɞɥɹ ɨɛɨɡɧɚɱɟɧɢɹ ɫɚɦɨɣ ɮɭɧɤɰɢɢ, ɟɟ ɚɪɝɭɦɟɧɬɚ ɢ ɟɟ ɡɧɚɱɟɧɢɣ ɤɪɨɦɟ ɛɭɤɜ f, x, y ɦɨɠɧɨ ɩɪɢɦɟɧɢɬɶ ɥɸɛɵɟ ɞɪɭɝɢɟ ɛɭɤɜɵ, ɚ ɦɨɠɟɬ ɛɵɬɶ, ɢ ɢɯ ɫɨɱɟɬɚɧɢɹ (ɟɫɥɢ ɧɟ ɩɪɨɩɭɫɤɚɬɶ, ɤɚɤ ɷɬɨ ɦɵ ɢ ɞɟɥɚɟɦ, ɡɧɚɤ u ɭɦɧɨɠɟɧɢɹ ɜ ɡɚɩɢɫɹɯ ɩɪɨɢɡɜɟɞɟɧɢɣ).
Ɍ ɚ ɛ ɥ ɢ ɱ ɧ ɵ ɣ ɫɩɨɫɨɛ ɡɚɞɚɬɶ ɮɭɧɤɰɢɸ ɫɨɫɬɨɢɬ ɜ ɬɨɦ, ɱɬɨ ɡɧɚɱɟɧɢɹ ɚɪɝɭɦɟɧɬɚ ɡɚɩɢɫɵɜɚɸɬ ɜ ɨɞɧɨɣ ɫɬɪɨɤɟ (ɜ ɨɞɧɨɦ ɫɬɨɥɛɰɟ), ɚ ɡɧɚɱɟɧɢɹ ɮɭɧɤɰɢɢ – ɜ ɞɪɭɝɨɣ ɫɬɪɨɤɟ (ɜ ɞɪɭɝɨɦ ɫɬɨɥɛɰɟ). ɉɪɚɜɢɥɨ f ɡɞɟɫɶ ɩɪɟɞɟɥɶɧɨ ɩɪɨɫɬɨɟ: ɩɨɞ ɤɚɠɞɵɦ (ɪɹɞɨɦ ɫ ɤɚɠɞɵɦ) ɡɧɚɱɟɧɢɟɦ ɬɚɛɥɢɱɧɨɝɨ ɚɪɝɭɦɟɧɬɚ xti – ɫɜɨɟ ɡɧɚɱɟɧɢɟ ɬɚɛɥɢɱɧɨɣ ɮɭɧɤɰɢɢ yti. Ɍɚɛɥɢɱɧɨ ɡɚɞɚɧɧɭɸ ɮɭɧɤɰɢɸ ɛɭɞɟɦ ɩɪɟɞɫɬɚɜɥɹɬɶ ɬɚɤɨɣ ɤɨɧɫɬɪɭɤɰɢɟɣ: {xti,yti}.
Ɍɚɛɥɢɰɭ ɦɨɠɧɨ ɩɨɫɬɪɨɢɬɶ ɩɨ ɚɧɚɥɢɬɢɱɟɫɤɨɦɭ ɜɵɪɚɠɟɧɢɸ ɮɭɧɤ-
ɰɢɢ. ɑɚɫɬɨ ɜ ɬɚɛɥɢɰɭ ɫɜɨɞɹɬ ɪɟ- |
|
|
|
|
Ɍɚɛɥɢɰɚ 4.1 |
||
ɡɭɥɶɬɚɬɵ ɷɤɫɩɟɪɢɦɟɧɬɚ, ɤɚɠɞɵɣ ɢɡ |
|
|
|
|
|||
ɤɨɬɨɪɵɯ ɧɟ ɢɦɟɟɬ ɫɨɨɬɜɟɬɫɬɜɭɸɳɟ- |
i |
0 |
1 |
2 |
|
3 |
4 |
ɝɨ ɚɧɚɥɢɬɢɱɟɫɤɨɝɨ ɨɩɢɫɚɧɢɹ. |
xti |
0.0 |
0.5 |
1.0 |
|
1.5 |
2.0 |
ȿɫɥɢ ɮɭɧɤɰɢɹ ɡɚɞɚɧɚ ɚɧɚɥɢ- |
|
||||||
yti |
0.00 |
0.03 |
0.25 |
|
0.84 |
2.00 |
|
ɬɢɱɟɫɤɢ, ɬɨ ɩɪɨɰɟɞɭɪɚ ɩɨɫɬɪɨɟɧɢɹ |
|
||||||
ɟɟ ɬɚɛɥɢɰɵ ɫɨɫɬɨɢɬ ɜ ɫɥɟɞɭɸɳɟɦ.
Ɉɛɥɚɫɬɶ ɨɩɪɟɞɟɥɟɧɢɹ ɮɭɧɤɰɢɢ ɨɝɪɚɧɢɱɢɜɚɸɬ ɨɬɪɟɡɤɨɦ [a,b]. ɇɚ ɷɬɨɦ ɨɬɪɟɡɤɟ ɡɚɞɚɸɬ ɫɟɬɤɭ
a xt0,xt1,xt2, |
,xti,xti+1, |
|
,xtn b |
|
|
||
|
y |
|
|||||
|
|
|
|
b a |
|
|
|
ɫ ɪɚɜɧɨɦɟɪɧɵɦ ɲɚɝɨɦ h |
|
, ɝɞɟ |
|
|
|||
|
|
|
|
||||
|
|
|
|
n |
|
|
|
n – ɨɛɴɟɦ ɬɚɛɥɢɰɵ. ɉɨɧɹɬɧɨ, ɱɬɨ |
|
|
|||||
xti a iuh, i |
0,n |
. ɗɬɨ ɫɨɞɟɪɠɢɦɨɟ |
|
|
|||
ɩɟɪɜɨɣ ɫɬɪɨɤɢ ɛɭɞɭɳɟɣ ɬɚɛɥɢɰɵ. |
|
x |
|||||
Ⱦɥɹ ɤɚɠɞɨɝɨ ɡɧɚɱɟɧɢɹ xti ɩɨ |
|
|
|||||
ɮɨɪɦɭɥɟ yti f(xti) ɜɵɱɢɫɥɹɸɬ ɨɬɫɱɟ- |
|
Ɋɢɫ. 4.2 |
|||||
ɬɵ ɬɚɛɥɢɱɧɨɣ |
ɮɭɧɤɰɢɢ. |
Ɍɚɤ ɩɨɥɭ- |
|
||||
|
|
||||||
45

ɱɚɸɬ ɜɬɨɪɭɸ ɫɬɪɨɤɭ ɬɚɛɥɢɰɵ. ɍɞɨɛɧɨ ɛɵɜɚɟɬ ɞɨɩɨɥɧɢɬɶ ɬɚɛɥɢɰɭ ɟɳɟ ɨɞɧɨɣ (ɜɟɪɯɧɟɣ) ɫɬɪɨɤɨɣ ɫ ɧɨɦɟɪɚɦɢ 0, 1,…, i, i 1,…, n ɟɟ ɨɬɫɱɟɬɨɜ.
ɉɨɫɬɪɨɢɦ ɞɥɹ ɩɪɢɦɟɪɚ ɬɚɛɥɢɰɭ ɩɨ ɚɧɚɥɢɬɢɱɟɫɤɨɦɭ ɜɵɪɚɠɟ-
ɧɢɸ (4.1).
Ɉɝɪɚɧɢɱɢɦɫɹ ɨɬɪɟɡɤɨɦ [0,2] ɢ n 4. ɂɦɟɟɦ:
h b a 0.5, n
xti a iuh,
yti 0.25u(xti)3.
ȼ ɪɟɡɭɥɶɬɚɬɟ ɩɨɥɭɱɢɦ ɬɚɛɥ.4.1.
Ⱥɧɚɥɢɬɢɱɟɫɤɢɣ ɢ ɬɚɛɥɢɱɧɵɣ ɫɩɨɫɨɛɵ ɡɚɞɚɧɢɹ ɮɭɧɤɰɢɢ ɧɟɞɨɫɬɚɬɨɱɧɨ ɧɚɝɥɹɞɧɵ. ɗɬɨ ɨɛɭɫɥɨɜɥɢɜɚɟɬ ɩɪɢɦɟɧɟɧɢɟ ɝ ɪ ɚ ɮ ɢ ɱ ɟ ɫ ɤ ɨ ɝ ɨ ɫɩɨɫɨɛɚ ɡɚɞɚɧɢɹ ɮɭɧɤɰɢɢ. Ɉɛɵɱɧɨ ɝɪɚɮɢɤ ɞɨɩɨɥɧɹɟɬ ɞɪɭɝɢɟ ɫɩɨɫɨɛɵ ɡɚɞɚɧɢɹ ɮɭɧɤɰɢɢ. ɋɬɪɨɢɬɫɹ ɝɪɚɮɢɤ ɜɫɟɝɞɚ ɩɨ ɬɚɛɥɢɰɟ, ɱɚɳɟ ɜɫɟɝɨ ɜ ɞɟɤɚɪɬɨɜɵɯ ɤɨɨɪɞɢɧɚɬɚɯ. Ⱦɟɤɚɪɬɨɜɚ ɫɢɫɬɟɦɚ ɤɨɨɪɞɢɧɚɬ ɨɛɪɚɡɨɜɚɧɚ ɞɜɭɦɹ ɜɡɚɢɦɧɨ ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɵɦɢ ɩɪɹɦɵɦɢ. Ƚɨɪɢɡɨɧɬɚɥɶɧɚɹ ɩɪɹɦɚɹ – ɷɬɨ ɨɫɶ ɚɛɫɰɢɫɫ 0x, ɜɟɪɬɢɤɚɥɶɧɚɹ ɩɪɹɦɚɹ – ɨɫɶ ɨɪɞɢɧɚɬ 0y. Ɍɨɱɤɚ ɩɟɪɟɫɟɱɟɧɢɹ ɨɫɟɣ ɫɥɭɠɢɬ ɧɚɱɚɥɨɦ ɤɨɨɪɞɢɧɚɬ. ɇɚ ɤɚɠɞɨɣ ɢɡ ɨɫɟɣ ɡɚɞɚɸɬ ɧɚɩɪɚɜɥɟɧɢɟ ɜɨɡɪɚɫɬɚɧɢɹ ɨɬɫɱɟɬɨɜ, ɚ ɩɪɢ ɧɟɨɛɯɨɞɢɦɨɫɬɢ ɢ ɦɚɫɲɬɚɛ (ɟɞɢɧɢɱɧɵɣ ɨɬɪɟɡɨɤ).
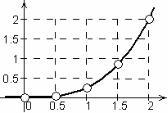
ɂɬɚɤ, ɫɧɚɱɚɥɚ ɫɬɪɨɢɬɫɹ ɬɚɛɥɢɰɚ {xti,yti}. ɉɨ ɞɚɧɧɵɦ ɷɬɨɣ ɬɚɛɥɢɰɵ ɫɬɪɨɢɬɫɹ ɬɨɱɟɱɧɵɣ ɝɪɚɮɢɤ. Ʉɚɠɞɨɣ ɩɚɪɟ ɱɢɫɟɥ xti ɢ yti ɢɡ ɤɨɥɨɧɤɢ ɬɚɛ-
ɥɢɰɵ ɧɨɦɟɪ i ɧɚ ɤɨɨɪɞɢɧɚɬɧɨɣ ɩɥɨɫɤɨɫɬɢ ɫɬɚɜɹɬ ɜ ɫɨɨɬɜɟɬɫɬɜɢɟ ɬɨɱɤɭ (xti,yti). ɗɬɢ ɬɨɱɤɢ ɧɚ ɝɪɚɮɢɤɟ ɫɨɟɞɢɧɹɸɬ ɩɥɚɜɧɨɣ ɤɪɢɜɨɣ. ɇɚ ɪɢɫ.4.2
ɩɨɤɚɡɚɧ ɝɪɚɮɢɤ, ɩɨɫɬɪɨɟɧɧɵɣ ɩɨ ɬɚɛɥ. 4.1. Ɂɞɟɫɶ ɤɪɭɠɨɱɤɚɦɢ ɩɨɤɚɡɚɧɵ ɬɨɱɤɢɬɚɛɥɢɱɧɨɣɮɭɧɤɰɢɢ, ɢɨɧɢɫɨɟɞɢɧɟɧɵɩɥɚɜɧɨɣɥɢɧɢɟɣ.
|
|
|
|
Ɉɛɪɚɬɧɚɹ ɮɭɧɤɰɢɹ. ɉɭɫɬɶ ɮɭɧɤɰɢɹ f ɢɦɟɟɬ |
|
g |
Y |
ɞɥɹ y ɪɨɜɧɨ ɫɬɨɥɶɤɨ ɠɟ ɪɚɡɧɵɯ ɡɧɚɱɟɧɢɣ, ɫɤɨɥɶ- |
|
X |
||||
|
|
|
|
ɤɨ ɡɧɚɱɟɧɢɣ ɢɦɟɟɬ ɢ ɟɟ ɚɪɝɭɦɟɧɬ x. Ɉɬɫɸɞɚ ɫɥɟ- |
|
|
|
|
|
|
|
|
y |
ɞɭɟɬ, ɱɬɨ ɭɪɚɜɧɟɧɢɟ f(x) y ɜɫɟɝɞɚ ɦɨɠɧɨ ɪɚɡɪɟ- |
xɲɢɬɶ ɨɬɧɨɫɢɬɟɥɶɧɨ x ɢ ɡɚɩɢɫɚɬɶ x g(y).
Ɏɭɧɤɰɢɹ g, ɤɨɬɨɪɚɹ ɫɬɚɜɢɬ ɜ ɫɨɨɬɜɟɬɫɬɜɢɟ ɤɚɠɞɨɦɭ ɷɥɟɦɟɧɬɭ y Y ɟɞɢɧɫɬɜɟɧɧɵɣ
ɷɥɟɦɟɧɬ x X, ɬɚɤɨɣ, ɱɬɨ y f(x), ɧɚɡɵɜɚɟɬɫɹ ɨɛɪɚɬɧɨɣ ɤ ɮɭɧɤɰɢɢ f (ɪɢɫ.4.3).
Ɏɭɧɤɰɢɸ f ɧɚɡɵɜɚɸɬ ɩɪɹɦɨɣ (ɢɫɯɨɞɧɨɣ). Ɉɛɥɚɫɬɶ ɨɩɪɟɞɟɥɟɧɢɹ ɨɛɪɚɬɧɨɣ ɮɭɧɤɰɢɢ ɫɨɜɩɚɞɚɟɬ ɫ ɨɛɥɚɫɬɶɸ ɡɧɚɱɟɧɢɣ ɢɫɯɨɞɧɨɣ ɮɭɧɤɰɢɢ
Dg Ef ɢ, ɧɚɨɛɨɪɨɬ, Eg Df . Ɏɭɧɤɰɢɹ, ɨɛɪɚɬɧɚɹ ɤ g, ɟɫɬɶ ɩɪɹɦɚɹ ɮɭɧɤɰɢɹ f. Ɂɧɚɱɢɬ, ɮɭɧɤɰɢɢ f ɢ g – ɜɡɚɢɦɧɨ ɨɛɪɚɬɧɵɟ.
46
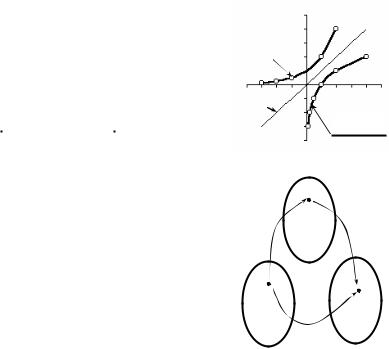
ɉɭɫɬɶ ɢɫɯɨɞɧɚɹ ɮɭɧɤɰɢɹ y 2x. ɉɨɫɬɪɨɢɦ ɟɟ ɝɪɚɮɢɤ. Ⱦɥɹ ɷɬɨɝɨ ɫɨɫɬɚɜɢɦ ɬɚɛɥ.4.2, ɩɨɫɬɪɨɢɦ ɬɨɱɟɱɧɵɣ ɝɪɚɮɢɤ ɢ ɫɨɟɞɢɧɢɦ ɬɨɱɤɢ,
ɡɚɞɚɧɧɵɟ ɬɚɛɥɢɰɟɣ, ɩɥɚɜɧɨɣ |
ɥɢɧɢɟɣ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ɪɢɫ.4.4). Ʉɚɤ ɜɢɞɢɦ, ɷɬɚ ɮɭɧɤɰɢɹ ɜɨɡɪɚɫ- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|||
ɬɚɟɬ ɧɚ ɜɫɟɣ ɱɢɫɥɨɜɨɣ ɨɫɢ ɢ ɨɝɪɚɧɢɱɟɧɚ |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ɫɧɢɡɭ ɨɫɶɸ ɚɛɫɰɢɫɫ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 2x |
|
|
|
|
|
|
|
|
|||||
Ⱥ ɬɟɩɟɪɶ ɧɚɣɞɟɦ ɮɭɧɤɰɢɸ, ɨɛɪɚɬɧɭɸ |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
ɤ y 2x, ɢ ɩɨɫɬɪɨɢɦ ɟɟ ɝɪɚɮɢɤ ɜ ɬɟɯ ɠɟ (!) |
|
|
|
|
|
|
|
|
|
|
x |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
ɤɨɨɪɞɢɧɚɬɚɯ, ɱɬɨ ɢ ɝɪɚɮɢɤ ɩɪɹɦɨɣ ɮɭɧɤ- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
y x |
|
|
|
|
|
|
|
|
|
||||||
|
ɰɢɢ. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɍɚɛɥɢɰɚ 4.2 |
Ⱦɥɹ |
|
|
|
|
|
|
|
|
|
y log2(x) |
||||
f(x) |
x |
3 |
2 |
1 |
0 |
1 |
2 |
y |
g(x) |
||||||
y |
|
1 |
|
|
1 |
|
|
1 |
|
1 |
2 |
4 |
x |
||
|
|
|
|
|
|||||||||||
|
8 |
|
4 |
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||
ɷɬɨɝɨ ɜ
ɡɚɩɢɫɢ ɢɫɯɨɞ- Ɋɢɫ. 4.4
ɧɨɣ
ɮɭɧɤ- |
|
|
|
|
|
|
|
|
|
ɰɢɢ ɩɨɦɟɧɹɟɦ ɦɟɫɬɚɦɢ x ɢ y: x 2y. ɂɡ ɷɬɨ- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
f |
||
ɝɨ ɭɪɚɜɧɟɧɢɹ ɧɚɣɞɟɦ y: y log2(x). ɗɬɨ ɢ |
g |
|
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
ɟɫɬɶ ɮɭɧɤɰɢɹ, ɨɛɪɚɬɧɚɹ ɤ ɢɫɯɨɞɧɨɣ y 2x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɍɚɛɥɢɰɭ ɨɛɪɚɬɧɨɣ ɮɭɧɤɰɢɢ ɩɨɥɭɱɚɸɬ ɢɡ |
|
|
|
|
|
|
|
|
|
ɬɚɛɥɢɰɵ ɢɫɯɨɞɧɨɣ, ɩɨɦɟɧɹɜ ɜ ɧɟɣ ɦɟɫɬɚ- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
||
|
|
|
X |
|
|
|
|
||
ɦɢ ɨɛɨɡɧɚɱɟɧɢɹ ɫɬɪɨɤ (ɬɚɛɥ. 4.2). ɉɨ ɷɬɨɣ |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
z |
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
ɬɚɛɥɢɰɟ ɢ ɫɬɪɨɢɦ ɝɪɚɮɢɤ ɨɛɪɚɬɧɨɣ ɮɭɧɤ- |
|
|
|
|
|
h |
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
ɰɢɢ (ɪɢɫ.4.4). Ʉɚɤ ɜɢɞɢɦ, ɷɬɨ ɮɭɧɤɰɢɹ – |
|
|
|
|
|
|
|
|
|
ɜɨɡɪɚɫɬɚɸɳɚɹ ɩɪɢ x!0, ɢ ɨɧɚ ɧɟ ɨɝɪɚɧɢɱɟɧɚ.
Ⱦɚɧɧɵɣ ɩɪɢɦɟɪ ɢɥɥɸɫɬɪɢɪɭɟɬ ɨɛɳɟɟ ɫɜɨɣɫɬɜɨ ɜɡɚɢɦɧɨ ɨɛɪɚɬɧɵɯ ɮɭɧɤ-
ɰɢɣ: ɝɪɚɮɢɤɢ ɢɫɯɨɞɧɨɣ ɢ ɨɛɪɚɬɧɨɣ ɮɭɧɤɰɢɣ ɢɦɟɸɬ ɨɫɶɸ ɫɢɦɦɟɬɪɢɢ ɩɪɹɦɭɸ y x (ɤɨɝɞɚ ɦɚɫɲɬɚɛɵ ɩɨ ɨɫɹɦ ɤɨɨɪɞɢɧɚɬ ɨɞɢɧɚɤɨɜɵ).
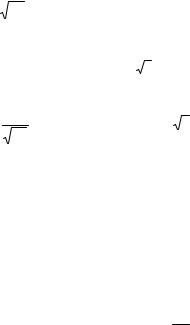
ɋɥɨɠɧɚɹ ɮɭɧɤɰɢɹ. ɉɭɫɬɶ ɡɚɞɚɧɵ ɮɭɧɤɰɢɢ s g(x) ɢ z f(s) ɬɚɤɢɟ, ɱɬɨ ɨɛɥɚɫɬɶ ɨɩɪɟɞɟɥɟɧɢɹ ɮɭɧɤɰɢɢ f ɫɨɜɩɚɞɚɟɬ ɫ ɨɛɥɚɫɬɶɸ ɡɧɚɱɟɧɢɣ ɮɭɧɤɰɢɢ g (ɪɢɫ.4.5). Ɏɭɧɤɰɢɹ g ɨɬɨɛɪɚɠɚɟɬ ɦɧɨɠɟɫɬɜɨ X ɧɚ ɦɧɨɠɟɫɬɜɨ Y, ɚ ɮɭɧɤɰɢɹ f ɨɬɨɛɪɚɠɚɟɬ ɦɧɨɠɟɫɬɜɨ Y ɧɚ ɦɧɨɠɟɫɬɜɨ Z. ɗɬɢ ɞɜɚ ɨɬɨɛɪɚɠɟɧɢɹ ɜɦɟɫɬɟ ɡɚɞɚɸɬ ɧɨɜɨɟ ɨɬɨɛɪɚɠɟɧɢɟ h ɦɧɨɠɟɫɬɜɚ X ɧɚ ɦɧɨɠɟɫɬɜɨ Z. Ɍɚɤɨɟ ɨɬɨɛɪɚɠɟɧɢɟ ɢ ɧɚɡɵɜɚɟɬɫɹ ɫɥɨɠɧɨɣ ɮɭɧɤɰɢɟɣ (ɫɭɩɟɪɩɨɡɢɰɢɟɣ ɮɭɧɤɰɢɣ f ɢ g):
z f(g(x)) h(x).
ɇɚɩɪɢɦɟɪ,
s g(x) sin(x), f(s) s2.
Ɍɨɝɞɚ
47
z f(g(x)) (sin(x))2 h(x).
ȿɫɥɢ ɠɟ
s g(x) x2, ɚ f(s) sin(s),
ɬɨ
z f(g(x)) sin(x2) h(x).
ȼ ɫɭɩɟɪɩɨɡɢɰɢɢ ɮɭɧɤɰɢɣ f(g(x)) ɮɭɧɤɰɢɸ s g(x) ɧɚɡɵɜɚɸɬ ɜɥɨɠɟɧɧɨɣ, ɚ ɮɭɧɤɰɢɸ f(s) ɧɚɡɵɜɚɸɬ ɜɧɟɲɧɟɣ.
ɇɚ ɩɪɚɤɬɢɤɟ ɩɪɨɛɥɟɦɚ ɫɨɫɬɨɢɬ ɜ ɬɨɦ, ɱɬɨ ɡɚɞɚɧɧɨɣ ɹɜɥɹɟɬɫɹ ɮɭɧɤɰɢɹ h(x), ɚ ɧɭɠɧɨ ɛɵɜɚɟɬ ɧɚɣɬɢ ɢ ɜɵɞɟɥɢɬɶ ɜɥɨɠɟɧɧɭɸ ɢ ɜɧɟɲɧɸɸ ɮɭɧɤɰɢɢ. Ⱦɥɹ ɷɬɨɝɨ ɩɨɫɬɭɩɚɸɬ ɬɚɤ. Ɇɵɫɥɟɧɧɨ ɡɚɞɚɸɬ ɡɧɚɱɟɧɢɟ ɚɪɝɭɦɟɧɬɚ x ɢ ɮɢɤɫɢɪɭɸɬ ɬɟ ɞɟɣɫɬɜɢɹ ɜ h(x), ɤɨɬɨɪɵɟ ɜɵɩɨɥɧɹɸɬɫɹ ɧɚɞ ɧɢɦ ɜ ɩɟɪɜɭɸ ɨɱɟɪɟɞɶ. ɗɬɢ ɞɟɣɫɬɜɢɹ ɢ ɨɛɪɚɡɭɸɬ ɜɥɨɠɟɧɧɭɸ ɮɭɧɤɰɢɸ s g(x). Ⱦɚɥɟɟ ɨɩɪɟɞɟɥɹɸɬ ɬɟ ɞɟɣɫɬɜɢɹ ɜ h(x), ɤɨɬɨɪɵɟ ɩɪɨɢɡɜɨɞɹɬɫɹ ɧɚɞ s – ɪɟɡɭɥɶɬɚɬɨɦ ɜɥɨɠɟɧɧɨɣ ɮɭɧɤɰɢɢ. Ɉɧɢ ɢ ɫɨɫɬɚɜɥɹɸɬ ɜɧɟɲɧɸɸ ɮɭɧɤɰɢɸ z f(s). ɇɚɩɪɢɦɟɪ,
h(x) 5 x3 .
Ɂɞɟɫɶ ɜ ɩɟɪɜɭɸ ɨɱɟɪɟɞɶ x ɜɨɡɜɨɞɹɬ ɜ ɤɭɛ, ɚ ɢɡ ɩɨɥɭɱɟɧɧɨɝɨ ɪɟɡɭɥɶɬɚɬɚ ɢɡɜɥɟɤɚɸɬ ɤɨɪɟɧɶ ɩɹɬɨɣ ɫɬɟɩɟɧɢ, ɡɧɚɱɢɬ,
s g(x) x3, |
|
z f(s) 5 s . |
|
|
|
|
Ɇɨɠɧɨ ɫɨɫɬɚɜɢɬɶ ɫɭɩɟɪɩɨɡɢɰɢɸ ɢɡ ɬɪɟɯ ɢ ɛɨɥɟɟ ɮɭɧɤɰɢɣ. ɇɚ- |
||||||
ɩɪɢɦɟɪ, |
|
|
|
1 |
|
|
h(x) 1 . |
s x3, |
z 5 s , |
v |
. |
||
|
||||||
5 x3 |
|
|
|
z |
||
4.2.Аппроксимация функций
Ⱥɩ ɩ ɪ ɨ ɤ ɫ ɢ ɦ ɚ ɰ ɢ ɹ – ɷɬɨ ɡɚɦɟɧɚ ɮɭɧɤɰɢɢ f(x) ɧɚ ɨɬɪɟɡɤɟ [a,b] ɩɨɞɯɨɞɹɳɟɣ ɮɨɪɦɭɥɨɣ M(x) ɬɚɤɨɣ, ɱɬɨɛɵ ɩɨɝɪɟɲɧɨɫɬɶ ɡɚɦɟɧɵ µM(x) f(x) µ ɧɟ ɩɪɟɜɵɲɚɥɚ ɛɵ ɞɨɩɭɫɬɢɦɵɯ ɡɧɚɱɟɧɢɣ.
Ⱦɥɹ ɜɵɩɨɥɧɟɧɢɹ ɚɩɩɪɨɤɫɢɦɚɰɢɢ ɮɭɧɤɰɢɸ f(x) ɧɚ ɨɬɪɟɡɤɟ [a,b] ɩɪɟɞɫɬɚɜɥɹɸɬ ɬɚɛɥɢɰɟɣ {xti,yti}. Ⱦɥɹ ɷɬɨɝɨ ɨɬɪɟɡɨɤ [a,b] ɪɚɡɛɢɜɚɸɬ ɧɚ n ɱɚɫɬɟɣ ɢ ɩɨɥɭɱɚɸɬ ɧɚɛɨɪ ɡɧɚɱɟɧɢɣ ɚɪɝɭɦɟɧɬɚ ɬɚɛɥɢɱɧɨɣ ɮɭɧɤɰɢɢ a xt0, xt1, xt2, , xtk, xtk 1, xtn 1, xtn b, ɚ ɩɨ ɮɨɪɦɭɥɟ f(x) ɜɵɱɢɫɥɹɸɬ
ɧɚɛɨɪ ɨɬɫɱɟɬɨɜ ɬɚɛɥɢɱɧɨɣ ɮɭɧɤɰɢɢ yti f(xti), i 0,n (ɱɢɫɥɨ n – ɨɛɴɟɦ ɬɚɛɥɢɰɵ). ɉɨ ɞɚɧɧɵɦ ɷɬɨɣ ɬɚɛɥɢɰɵ {xti,yti} ɢ ɩɨɞɛɢɪɚɸɬ ɩɨɞɯɨɞɹɳɭɸ ɮɨɪɦɭɥɭ M(x).
ȼɵɱɢɫɥɟɧɢɟ y ɩɨ ɮɨɪɦɭɥɟ M(x), ɤɨɝɞɚ x ɥɟɠɢɬ ɜɧɭɬɪɢ ɬɚɛɥɢɰɵ (xt0dxd xtn), ɧɚɡɵɜɚɸɬ ɢ ɧ ɬ ɟ ɪ ɩ ɨ ɥ ɹ ɰ ɢ ɟ ɣ ɮɭɧɤɰɢɢ {xti,yti}. Ʉɨɝɞɚ ɠɟ
48
x ɥɟɠɢɬ ɜɧɟ ɬɚɛɥɢɰɵ, ɨɩɪɟɞɟɥɟɧɢɟ ɡɧɚɱɟɧɢɹ y M(x) ɧɚɡɵɜɚɸɬ ɷ ɤ ɫ ɬ - ɪ ɚ ɩ ɨ ɥ ɹ ɰ ɢ ɟ ɣ ɮɭɧɤɰɢɢ {xti,yti}. ȿɫɥɢ x xt0, ɬɨ ɢɦɟɟɬ ɦɟɫɬɨ ɷɤɫɬɪɚɩɨɥɹɰɢɹ ɧ ɚ ɡ ɚ ɞ , ɟɫɥɢ ɠɟ x!xtn, ɷɤɫɬɪɚɩɨɥɹɰɢɹ ɜ ɩ ɟ ɪ ɟ ɞ . ɉɪɢɦɟɪɨɦ ɷɤɫɬɪɚɩɨɥɹɰɢɢ ɜɩɟɪɟɞ ɛɭɞɟɬ ɩɪɨɝɧɨɡ ɩɨɤɚɡɚɬɟɥɟɣ ɩɪɟɫɬɭɩɧɨɫɬɢ ɧɚ ɫɥɟɞɭɸɳɢɣ ɝɨɞ ɩɨ ɪɟɡɭɥɶɬɚɬɚɦ ɢɡɦɟɪɟɧɢɣ ɟɟ ɩɚɪɚɦɟɬɪɨɜ ɜ ɩɪɟɞɵɞɭɳɢɟ ɝɨɞɵ.
Ʉɨɝɞɚ ɢ ɞɥɹ ɱɟɝɨ ɩɪɢɦɟɧɹɸɬ ɚɩɩɪɨɤɫɢɦɚɰɢɸ?
ɉɟɪɜɨɟ, ɤɨɝɞɚ f(x) – ɫɥɨɠɧɚɹ ɮɨɪɦɭɥɚ, ɢ ɩɨɥɭɱɟɧɢɟ ɛɨɥɶɲɨɝɨ ɦɚɫɫɢɜɚ ɜɟɥɢɱɢɧ y f(x) ɬɪɟɛɭɟɬ ɡɧɚɱɢɬɟɥɶɧɵɯ ɜɵɱɢɫɥɢɬɟɥɶɧɵɯ ɡɚɬɪɚɬ. Ɍɨɝɞɚ ɮɨɪɦɭɥɭ f(x) ɢɫɩɨɥɶɡɭɸɬ ɬɨɥɶɤɨ ɞɥɹ ɩɨɫɬɪɨɟɧɢɹ ɬɚɛɥɢɰɵ {xti,yti} ɨɛɴɟɦɨɦ n, ɚ ɨɫɧɨɜɧɨɣ ɦɚɫɫɢɜ ɡɧɚɱɟɧɢɣ y ɜɵɱɢɫɥɹɸɬ ɩɨ ɛɨɥɟɟ ɩɪɨɫɬɨɣ ɮɨɪɦɭɥɟ M(x).
ȼɬɨɪɨɟ, ɤɨɝɞɚ ɮɭɧɤɰɢɹ ɡɚɞɚɧɚ ɬɨɥɶɤɨ ɬɚɛɥɢɰɟɣ {xti,yti}, ɩɨɥɭɱɟɧɧɨɣ ɜ ɯɨɞɟ ɢɫɫɥɟɞɨɜɚɧɢɣ, ɷɤɫɩɟɪɢɦɟɧɬɚ, ɢɫɩɵɬɚɧɢɣ. Ɉɞɧɚɤɨ ɢ ɞɥɹ ɬɚɤɢɯ ɬɚɛɥɢɱɧɵɯ ɮɭɧɤɰɢɣ ɛɵɜɚɟɬ ɧɟɨɛɯɨɞɢɦɨ ɡɧɚɬɶ ɡɧɚɱɟɧɢɹ y ɞɥɹ ɥɸɛɵɯ xzxti. Ɏɨɪɦɭɥɚ M(x), ɩɨɫɬɪɨɟɧɧɚɹ ɩɨ ɞɚɧɧɵɦ ɬɚɛɥɢɰɵ, ɨɤɚɡɵɜɚɟɬɫɹ ɟɞɢɧɫɬɜɟɧɧɵɦ ɫɪɟɞɫɬɜɨɦ ɞɥɹ ɪɟɲɟɧɢɹ ɬɚɤɨɣ ɡɚɞɚɱɢ.
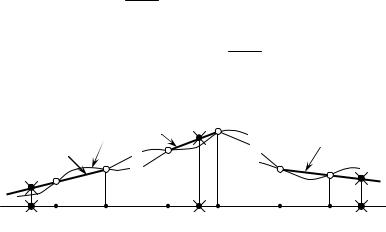
ɋɚɦɵɣ ɩɪɨɫɬɨɣ ɫɩɨɫɨɛ ɚɩɩɪɨɤɫɢɦɚɰɢɢ ɮɭɧɤɰɢɢ ɨɫɧɨɜɚɧ ɧɚ ɬɨɦ, ɱɬɨ ɤɚɠɞɵɟ ɞɜɟ ɫɨɫɟɞɧɢɟ ɬɨɱɤɢ ɧɚ ɝɪɚɮɢɤɟ ɬɚɛɥɢɱɧɨɣ ɮɭɧɤɰɢɢ
(xtk,ytk) ɢ (xtk+1,ytk+1) (k 0,n 1,) ɫɨɟɞɢɧɹɸɬ ɩɪɹɦɨɣ ɥɢɧɢɟɣ (ɪɢɫ. 4.6).
Ɍɚɤɚɹ ɚɩɩɪɨɤɫɢɦɚɰɢɹ ɧɚɡɵɜɚɟɬɫɹ ɥ ɢ ɧ ɟ ɣ ɧ ɨ ɣ . ɍɪɚɜɧɟɧɢɟ ɨɬɪɟɡɤɚ ɩɪɹɦɨɣ Mk(x) ɢ ɛɭɞɟɬ ɩɨɞɯɨɞɹɳɟɣ ɮɨɪɦɭɥɨɣ, ɩɨ ɤɨɬɨɪɨɣ ɜɵɱɢɫɥɹɟɬɫɹ
y ɞɥɹ ɥɸɛɨɝɨ x [xtk, xtk+1]. ɉɨɫɤɨɥɶɤɭ k 0,n 1, ɩɪɢ ɥɢɧɟɣɧɨɣ ɚɩɩɪɨɤɫɢɦɚɰɢɢ ɢɦɟɟɦ n ɭɪɚɜɧɟɧɢɣ ɜɢɞɚ Mk(x), ɬɨ ɟɫɬɶ n ɩɨɞɯɨɞɹɳɢɯ ɮɨɪɦɭɥ ɫ ɧɨɦɟɪɚɦɢ ɨɬ 0 ɞɨ n 1 (ɪɢɫ. 4.6). Ɉɬɦɟɬɢɦ, ɱɬɨ ɧɨɦɟɪ k ɮɨɪɦɭɥɵ ɢ
M0(x) |
f(x) |
Mk(x) |
y1 |
|
|
Mn-1(x) |
|
|
|
|
|
||
|
|
|
|
|
y3 |
|
y2 |
|
|
|
|
|
|
yt1 |
|
ytk |
ytk+1 |
ytn-1 |
ytn |
|
yt0 |
|
|||||
x2 xt0 |
xt1 |
... |
xtk x1 |
xtk+1 ... |
xtn-1 |
xtn x3 |
|
|
|
Ɋɢɫ.4.6 |
|
|
|
ɨɬɪɟɡɤɚ ɫɨɜɩɚɞɚɟɬ ɫ ɧɨɦɟɪɨɦ ɬɨɱɤɢ, ɜ ɤɨɬɨɪɨɣ ɷɬɨɬ ɨɬɪɟɡɨɤ ɧɚɱɢɧɚɟɬɫɹ.
Ɏɨɪɦɭɥɭ ɞɥɹ Mk(x) ɩɨɥɭɱɢɦ ɬɚɤ. ɇɚ ɪɢɫ. 4.7 ɩɨɤɚɡɚɧ ɮɪɚɝɦɟɧɬ ɝɪɚɮɢɤɚ ɬɚɛɥɢɱɧɨɣ ɮɭɧɤɰɢɢ ɧɚ ɨɬɪɟɡɤɟ [xtk, xtk+1]. Ɂɚɞɚɞɢɦ ɧɚ ɷɬɨɦ ɨɬɪɟɡɤɟ ɡɧɚɱɟɧɢɟ x ɢ ɨɬɦɟɬɢɦ ɧɚ ɨɬɪɟɡɤɟ ɩɪɹɦɨɣ, ɫɨɟɞɢɧɹɸɳɟɣ ɬɨɱɤɢ yk ɢ yk 1, ɡɧɚɱɟɧɢɟ y Mk(x). Ʉɚɤ ɜɢɞɢɦ,
49

y Mk(x) yk 'y. |
|
|
|
|
|
|
|
ȼɟɥɢɱɢɧɭ 'y ɧɚɣɞɟɦ ɢɡ ɩɨɞɨɛɢɹ ɩɪɹɦɨ- |
|
y |
Mk(x) |
yk 1 |
|||
ɭɝɨɥɶɧɵɯ ɬɪɟɭɝɨɥɶɧɢɤɨɜ, ɨɞɢɧ ɢɡ ɤɨɬɨ- |
|
|
|||||
|
|
|
|
||||
ɪɵɯ ɢɦɟɟɬ ɤɚɬɟɬɵ 'y ɢ x xk, ɚ ɞɪɭɝɨɣ – |
yk |
|
'y |
yk 1 yk |
|||
ɤɚɬɟɬɵ yk 1 yk ɢ xk 1 xk: |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
'y |
yk 1 yk |
. |
|
|
|
yk |
|
x xk |
xk 1 xk |
|
|
|
|
||
|
|
|
|
|
|
||
Ɉɬɫɸɞɚ |
|
|
|
xk |
|
x |
xk 1 |
'y yk 1 yk u x xk . |
|
Ɋɢɫ. 4.7 |
|
||||
|
|
|
|
||||
xk 1 xk |
|
|
|
|
|
|
|
ɉɨɞɫɬɚɜɢɜ ɧɚɣɞɟɧɧɨɟ 'y ɜ ɜɵɪɚɠɟɧɢɟ y |
Mk(x) |
yk 'y, ɩɨɥɭɱɢɦ ɢɫɤɨɦɨɟ |
|||||
y Mk(x) |
ytk 1 |
ytk |
u(x xtk), |
|
|
(4.2) |
|
ytk |
|
|
|
||||
|
xtk 1 xtk |
|
|
|
|
|
|
ɇɚɩɨɦɧɢɦ, ɱɬɨ ɡɞɟɫɶ k 0,n 1, ɬɨ ɟɫɬɶ ɮɨɪɦɭɥɨɣ (4.2) ɨɩɢɫɵɜɚɟɬ ɭɪɚɜɧɟɧɢɹ ɜɫɟɯ n ɨɬɪɟɡɤɨɜ ɧɚ ɪɢɫ. 4.6.
Ⱦɜɟ ɩɪɹɦɵɟ ɧɚ ɪɢɫ. 4.6 – ɨɫɨɛɵɟ. Ɏɨɪɦɭɥɭ ɞɥɹ ɫɚɦɨɣ ɥɟɜɨɣ ɢɡ ɧɢɯ M0(x) ɢɫɩɨɥɶɡɭɸɬ ɧɟ ɬɨɥɶɤɨ ɞɥɹ ɜɵɱɢɫɥɟɧɢɹ ɡɧɚɱɟɧɢɣ y ɧɚ ɨɬɪɟɡɤɟ [xt0,xt1], ɧɨ ɢ ɞɥɹ ɜɫɟɯ x xt0, ɬɨ ɟɫɬɶ ɞɥɹ ɷɤɫɬɪɚɩɨɥɹɰɢɢ ɧɚɡɚɞ. Ɏɨɪɦɭɥɭ ɞɥɹ ɫɚɦɨɣ ɩɪɚɜɨɣ ɩɪɹɦɨɣ Mn-1(x) ɢɫɩɨɥɶɡɭɸɬ ɢ ɞɥɹ ɷɤɫɬɪɚɩɨɥɹɰɢɢ ɜɩɟɪɟɞ, ɬɨ ɟɫɬɶ ɞɥɹ ɜɵɱɢɫɥɟɧɢɹ ɡɧɚɱɟɧɢɣ y ɩɪɢ ɜɫɟɯ x!xtn. ɇɚ ɪɢɫ. 4.6 ɧɚɯɨɠɞɟɧɢɟ ɡɧɚɱɟɧɢɹ y1 ɞɥɹ x1: y1 Mk(x1) – ɫɭɬɶ ɢɧɬɟɪɩɨɥɹɰɢɹ, ɡɧɚɱɟɧɢɹ y2 ɞɥɹ x2: y2 M0(x2) – ɷɤɫɬɪɚɩɨɥɹɰɢɹ ɧɚɡɚɞ, ɡɧɚɱɟɧɢɹ y3 ɞɥɹ x3: y3 Mn-1(x3) – ɷɤɫɬɪɚɩɨɥɹɰɢɹ ɜɩɟɪɟɞ.
ɇɨɦɟɪ k ɭɪɚɜɧɟɧɢɹ ɬɨɣ ɩɪɹɦɨɣ Mk(x), ɧɚ ɤɨɬɨɪɨɣ ɥɟɠɢɬ ɢɫɤɨɦɨɟ ɡɧɚɱɟɧɢɟ y, ɨɩɪɟɞɟɥɹɸɬ ɩɨ ɡɚɞɚɧɧɨɦɭ x ɬɚɤ:
|
0 |
|
|
|
|
ɩɪɢ |
x xt0, |
|
|
k(x) |
° |
1 |
|
|
|
ɩɪɢ |
x ! xtn, |
(4.3) |
|
®n |
|
|
|
||||||
|
°i |
|
ɩɪɢ xt |
|
d x d xt |
, i |
|
|
|
|
|
i |
0,n 1. |
|
|||||
|
¯ |
|
|
|
i 1 |
|
|
|
|
ȼ ɧɚɣɞɟɧɧɭɸ ɮɨɪɦɭɥɭ Mk(x) ɩɨɞɫɬɚɜɥɹɸɬ ɡɚɞɚɧɧɨɟ ɡɧɚɱɟɧɢɟ x, ɡɧɚɱɟɧɢɹ ytk, ytk+1, xtk, xtk+1 ɢɡ ɬɚɛɥɢɰɵ {xti,yti} ɢ ɜɵɱɢɫɥɹɸɬ ɢɫɤɨɦɨɟ ɡɧɚɱɟɧɢɟ y.
Ʌɨɦɚɧɚɹ Mk(x) (k 0,n 1) ɨɬɥɢɱɚɟɬɫɹ ɨɬ ɝɪɚɮɢɤɚ ɮɭɧɤɰɢɢ f(x), ɩɨ ɤɨɬɨɪɨɣ ɩɨɫɬɪɨɟɧɚ ɬɚɛɥɢɰɚ {xti,yti}. ɉɨɷɬɨɦɭ ɡɧɚɱɟɧɢɟ y Mk(x), ɩɨɥɭɱɟɧɧɨɟ ɩɨ ɚɩɩɪɨɤɫɢɦɢɪɭɸɳɟɣ ɮɨɪɦɭɥɟ, ɫɨɞɟɪɠɢɬ ɨɲɢɛɤɭ. Ɉɰɟɧɢɬɶ ɷɬɭ ɨɲɢɛɤɭ ɦɨɠɧɨ, ɫɪɚɜɧɢɜ ɪɟɡɭɥɶɬɚɬ ɚɩɩɪɨɤɫɢɦɚɰɢɢ ɫ ɬɨɱɧɵɦ ɡɧɚɱɟɧɢɟɦ yT f(x), ɫɤɚɠɟɦ, ɬɚɤ:
50
