
Математика для юристов - Д.А. Ловцова
.pdfɨɞɧɨɜɪɟɦɟɧɧɨ ɩɪɨɢɡɨɲɥɢ ɩɪɨɬɢɜɨɩɨɥɨɠɧɵɟ ɫɨɛɵɬɢɹ ºA ɢ ºB, ɚ ɢɦɟɧɧɨ, ºAuºB. ɇɨ ɷɬɨ – ɩɪɚɜɚɹ ɱɚɫɬɶ ɭɬɜɟɪɠɞɟɧɢɹ 10. Ɂɧɚɱɢɬ, ɢ ɜ ɰɟɥɨɦ ɨɧɨ ɜɟɪɧɨ.
7.3. Классическое определение вероятности
Ʉɚɠɞɨɟ ɫɥɭɱɚɣɧɨɟ ɫɨɛɵɬɢɟ ɨɛɥɚɞɚɟɬ ɬɨɣ ɢɥɢ ɢɧɨɣ ɫɬɟɩɟɧɶɸ ɜɨɡɦɨɠɧɨɫɬɢ, ɨɞɧɨ ɛɨɥɶɲɟɣ, ɞɪɭɝɨɟ ɦɟɧɶɲɟɣ. Ⱦɥɹ ɧɟɤɨɬɨɪɵɯ ɫɨɛɵɬɢɣ ɦɵ ɦɨɠɟɦ ɫɪɚɡɭ ɫɤɚɡɚɬɶ, ɤɚɤɨɟ ɢɡ ɧɢɯ ɛɨɥɟɟ ɜɨɡɦɨɠɧɨ, ɚ ɤɚɤɨɟ ɦɟɧɟɟ ɜɨɡɦɨɠɧɨ. Ɍɚɤ, ɫɨɛɵɬɢɟ «ɜɵɩɚɞɟɧɢɟ ɝɟɪɛɚ ɩɪɢ ɨɞɧɨɦ ɛɪɨɫɤɟ ɦɨɧɟɬɵ» ɛɨɥɟɟ ɜɨɡɦɨɠɧɨ, ɱɟɦ ɫɨɛɵɬɢɟ «ɜɵɩɚɞɟɧɢɟ ɬɪɟɯ ɝɟɪɛɨɜ ɩɪɢ ɬɪɟɯ ɛɪɨɫɤɚɯ ɦɨɧɟɬɵ». Ɉɬɧɨɫɢɬɟɥɶɧɨ ɞɪɭɝɢɯ ɫɨɛɵɬɢɣ ɚɧɚɥɨɝɢɱɧɵɯ ɜɵɜɨɞɨɜ ɫɪɚɡɭ ɫɞɟɥɚɬɶ ɧɟɥɶɡɹ. Ⱦɥɹ ɷɬɨɝɨ ɬɪɟɛɭɟɬɫɹ ɭɬɨɱɧɢɬɶ ɭɫɥɨɜɢɹ ɨɩɵɬɚ. Ɍɚɤ ɢɥɢ ɢɧɚɱɟ, ɹɫɧɨ, ɱɬɨ ɤɚɠɞɨɟ ɢɡ ɫɥɭɱɚɣɧɵɯ ɫɨɛɵɬɢɣ ɨɛɥɚɞɚɟɬ ɬɨɣ ɢɥɢ ɢɧɨɣ ɫɬɟɩɟɧɶɸ ɜɨɡɦɨɠɧɨɫɬɢ. ɑɬɨɛɵ ɤɨɥɢɱɟɫɬɜɟɧɧɨ ɯɚɪɚɤɬɟɪɢɡɨɜɚɬɶ ɫɬɟɩɟɧɶ ɜɨɡɦɨɠɧɨɫɬɢ ɫɨɛɵɬɢɹ, ɧɭɠɧɨ ɫ ɤɚɠɞɵɦ ɢɡ ɧɢɯ ɫɜɹɡɚɬɶ ɨɩɪɟɞɟɥɟɧɧɨɟ ɱɢɫɥɨ, ɤɨɬɨɪɨɟ ɬɟɦ ɛɨɥɶɲɟ, ɱɟɦ ɛɨɥɟɟ ɜɨɡɦɨɠɧɨ ɷɬɨ ɫɨɛɵɬɢɟ. Ɍɚɤɨɟ ɱɢɫɥɨ ɢ ɧɚɡɵɜɚɸɬ ɜɟɪɨɹɬɧɨɫɬɶɸ ɫɨɛɵɬɢɹ.
ɂɬɚɤ, ɜɟɪɨɹɬɧɨɫɬɶ ɫɥɭɱɚɣɧɨɝɨ ɫɨɛɵɬɢɹ ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɸ ɤɨɥɢɱɟɫɬɜɟɧɧɭɸ ɦɟɪɭ ɜɨɡɦɨɠɧɨɫɬɢ ɟɝɨ ɧɚɫɬɭɩɥɟɧɢɹ.
Ʉɥɚɫɫɢɱɟɫɤɢɣ ɦɟɬɨɞ ɜɵɱɢɫɥɟɧɢɹ ɜɟɪɨɹɬɧɨɫɬɟɣ ɫɮɨɪɦɢɪɨɜɚɥɫɹ ɜ XVII ɜɟɤɟ ɤɚɤ ɪɟɡɭɥɶɬɚɬ ɚɧɚɥɢɡɚ ɚɡɚɪɬɧɵɯ ɢɝɪ. ȼ ɨɫɧɨɜɟ ɤɥɚɫɫɢɱɟɫɤɨɝɨ ɨɩɪɟɞɟɥɟɧɢɹ ɜɟɪɨɹɬɧɨɫɬɢ ɥɟɠɢɬ ɩɨɧɹɬɢɟ ɪɚɜɧɨɜɨɡɦɨɠɧɨɫɬɢ ɢɫɯɨɞɨɜ ɫɥɭɱɚɣɧɨɝɨ ɷɤɫɩɟɪɢɦɟɧɬɚ.
Ɋ ɚ ɜ ɧ ɨ ɜ ɨ ɡ ɦ ɨ ɠ ɧ ɨ ɫ ɬ ɶ ɢɫɯɨɞɨɜ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɧɟɬ ɧɢɤɚɤɢɯ ɨɫɧɨɜɚɧɢɣ ɩɪɟɞɩɨɱɟɫɬɶ ɨɞɢɧ ɢɫɯɨɞ ɞɪɭɝɢɦ, ɜɫɟ ɢɫɯɨɞɵ ɢɡ ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɝɨ ɩɪɨɫɬɪɚɧɫɬɜɚ ɷɥɟɦɟɧɬɚɪɧɵɯ ɫɨɛɵɬɢɣ ɢɦɟɸɬ ɪɚɜɧɵɟ ɜɟɪɨɹɬɧɨɫɬɢ. ɇɚɩɪɢɦɟɪ, ɩɨɹɜɥɟɧɢɟ ɝɟɪɛɚ ɢɥɢ ɪɟɲɟɬɤɢ ɩɪɢ ɨɞɧɨɦ ɛɪɨɫɤɟ ɦɨɧɟɬɵ – ɢɫɯɨɞɵ ɪɚɜɧɨɜɨɡɦɨɠɧɵɟ. ɑɚɳɟ ɜɫɟɝɨ ɜɵɜɨɞ ɨ ɪɚɜɧɨɜɨɡɦɨɠɧɨɫɬɢ ɢɫɯɨɞɨɜ ɨɫɧɨɜɚɧ ɧɚ ɫɨɨɛɪɚɠɟɧɢɹɯ ɨ ɫɢɦɦɟɬɪɢɢ ɢ ɨɞɧɨɪɨɞɧɨɫɬɢ ɨɛɴɟɤɬɨɜ, ɧɚɞ ɤɨɬɨɪɵɦɢ ɩɪɨɢɡɜɨɞɢɬɫɹ ɫɥɭɱɚɣɧɵɣ ɷɤɫɩɟɪɢɦɟɧɬ (ɤɚɠɞɚɹ ɦɨɧɟɬɚ – ɬɨɧɤɢɣ, ɨɞɧɨɪɨɞɧɵɣ ɤɪɭɝ, ɚ ɤɚɠɞɵɣ ɢɝɪɚɥɶɧɵɣ ɤɭɛɢɤ – ɢɞɟɚɥɶɧɵɣ ɨɞɧɨɪɨɞɧɵɣ ɤɭɛ).
Ɋɚɫɫɦɨɬɪɢɦ ɢɫɩɵɬɚɧɢɟ, ɜ ɪɟɡɭɥɶɬɚɬɟ ɤɨɬɨɪɨɝɨ ɦɨɠɟɬ ɧɚɫɬɭɩɢɬɶ ɫɨɛɵɬɢɟ A. Ʉɚɠɞɵɣ ɢɫɯɨɞ, ɩɪɢɧɚɞɥɟɠɚɳɢɣ ɩɨɞɦɧɨɠɟɫɬɜɭ A, ɧɚɡɵɜɚɸɬ ɛ ɥ ɚ ɝ ɨ ɩ ɪ ɢ ɹ ɬ ɧ ɵ ɦ ɫɨɛɵɬɢɸ A. ɉɭɫɬɶ, ɧɚɩɪɢɦɟɪ, ɫɨɛɵɬɢɟ A – ɜɵɩɚɞɟɧɢɟ ɧɟɱɟɬɧɨɝɨ ɱɢɫɥɚ ɨɱɤɨɜ ɩɪɢ ɨɞɧɨɦ ɛɪɨɫɤɟ ɢɝɪɚɥɶɧɨɝɨ ɤɭɛɢɤɚ. ɉɨɧɹɬɧɨ, ɱɬɨ ɢɡ ɲɟɫɬɢ ɪɚɜɧɨɜɨɡɦɨɠɧɵɯ ɢɫɯɨɞɨɜ ɷɬɨɝɨ ɷɤɫɩɟɪɢɦɟɧɬɚ {1,2,3,4,5,6} ɛɥɚɝɨɩɪɢɹɬɧɵɦɢ ɫɨɛɵɬɢɸ A ɹɜɥɹɸɬɫɹ ɬɪɢ: {1,3,5}.
Ɍɟɩɟɪɶ ɦɨɠɧɨ ɞɚɬɶ ɤɥɚɫɫɢɱɟɫɤɨɟ ɨɩɪɟɞɟɥɟɧɢɟ ɜɟɪɨɹɬɧɨɫɬɢ.
ȼɟɪɨɹɬɧɨɫɬɶɸ ɫɨɛɵɬɢɹ A ɧɚɡɵɜɚɟɬɫɹ ɨɬɧɨɲɟɧɢɟ ɱɢɫɥɚ ɢɫɯɨɞɨɜ, ɛɥɚɝɨɩɪɢɹɬɧɵɯ ɫɨɛɵɬɢɸ A, ɤ ɱɢɫɥɭ ɜɫɟɯ ɜɨɡɦɨɠɧɵɯ ɢɫɯɨɞɨɜ ɢɫɩɵɬɚɧɢɹ.
101

ȼɟɪɨɹɬɧɨɫɬɶ ɫɨɛɵɬɢɹ A ɨɛɨɡɧɚɱɚɸɬ ɤɚɤ P(A), ɱɢɫɥɨ ɢɫɯɨɞɨɜ, ɛɥɚɝɨɩɪɢɹɬɧɵɯ A, ɤɚɤ m(A), ɱɢɫɥɨ ɜɫɟɯ ɜɨɡɦɨɠɧɵɯ ɢɫɯɨɞɨɜ ɤɚɤ m(:) n. Ɍɨɝɞɚ ɩɨ ɨɩɪɟɞɟɥɟɧɢɸ
P(A) |
m(A) |
. |
(7.9) |
|
|||
|
n |
|
|
ɇɚɩɪɢɦɟɪ, ɞɥɹ ɜɵɱɢɫɥɟɧɢɹ ɜɟɪɨɹɬɧɨɫɬɢ ɫɨɛɵɬɢɹ «ɜɵɩɚɞɟɧɢɟ ɧɟɱɟɬɧɨɝɨ ɱɢɫɥɚ ɨɱɤɨɜ ɩɪɢ ɨɞɧɨɦ ɛɪɨɫɤɟ ɢɝɪɚɥɶɧɨɝɨ ɤɭɛɢɤɚ» ɢɦɟɟɦ: m(A) 3, n 6. Ɂɧɚɱɢɬ,
P(A) m(A) 1 .
n2
ɂɡ ɨɩɪɟɞɟɥɟɧɢɹ ɜɟɪɨɹɬɧɨɫɬɢ ɜɵɬɟɤɚɸɬ ɫɥɟɞɭɸɳɢɟ ɟɟ ɫɜɨɣɫɬɜɚ.
1. ȼɟɪɨɹɬɧɨɫɬɶ ɞɨɫɬɨɜɟɪɧɨɝɨ ɫɨɛɵɬɢɹ ɪɚɜɧɚ ɟɞɢɧɢɰɟ. Ⱦɟɣɫɬɜɢɬɟɥɶɧɨ, ɱɢɫɥɨ ɢɫɯɨɞɨɜ, ɛɥɚɝɨɩɪɢɹɬɧɵɯ ɞɨɫɬɨɜɟɪɧɨɦɭ ɫɨɛɵɬɢɸ :, ɪɚɜɧɨ ɦɨɳɧɨɫɬɢ ɩɪɨɫɬɪɚɧɫɬɜɚ ɷɥɟɦɟɧɬɚɪɧɵɯ ɫɨɛɵɬɢɣ m(:) n. Ɂɧɚɱɢɬ, ɩɨ ɮɨɪɦɭɥɟ (7.9) ɢɦɟɟɦ
P(:) n 1. n
2. ȼɟɪɨɹɬɧɨɫɬɶ ɧɟɜɨɡɦɨɠɧɨɝɨ ɫɨɛɵɬɢɹ ɪɚɜɧɚ ɧɭɥɸ. ȼ ɫɚɦɨɦ ɞɟɥɟ, ɞɥɹ ɫɨɛɵɬɢɹ ɜ ɩɪɨɫɬɪɚɧɫɬɜɟ ɷɥɟɦɟɧɬɚɪɧɵɯ ɫɨɛɵɬɢɣ ɧɟɬ ɧɢ ɨɞɧɨɝɨ ɛɥɚɝɨɩɪɢɹɬɧɨɝɨ, ɬɨ ɟɫɬɶ m( ) 0, ɢ
P( ) 0 0. n
3. ȼɟɪɨɹɬɧɨɫɬɶ ɩɪɨɢɡɜɨɥɶɧɨɝɨ ɫɥɭɱɚɣɧɨɝɨ ɫɨɛɵɬɢɹ ɡɚɤɥɸɱɟɧɚ ɦɟɠɞɭ ɧɭɥɟɦ ɢ ɟɞɢɧɢɰɟɣ. Ⱦɟɣɫɬɜɢɬɟɥɶɧɨ, ɱɢɫɥɨ ɢɫɯɨɞɨɜ, ɛɥɚɝɨɩɪɢɹɬɧɵɯ ɫɥɭɱɚɣɧɨɦɭ ɫɨɛɵɬɢɸ A, ɧɚɯɨɞɢɬɫɹ ɜ ɩɪɟɞɟɥɚɯ 0dm(A)dn. Ɋɚɡɞɟɥɢɜ ɤɚɠɞɵɣɨɩɟɪɚɧɞɜɷɬɢɯɧɟɪɚɜɟɧɫɬɜɚɯɧɚ n, ɩɨɥɭɱɢɦ
0 d m(A) d n , ɢɥɢ 0dP(A)d1. n n n
4. ȼɟɪɨɹɬɧɨɫɬɶ ɫɨɛɵɬɢɹ ºA, ɩɪɨɬɢɜɨɩɨɥɨɠɧɨɝɨ ɫɨɛɵɬɢɸ A, ɜɵɱɢɫɥɹɟɬɫɹ ɬɚɤ:
P(ºA) 1 P(A). |
(7.10) |
ɑɢɫɥɨ ɢɫɯɨɞɨɜ, ɛɥɚɝɨɩɪɢɹɬɧɵɯ ɫɨɛɵɬɢɸ A, ɪɚɜɧɨ m(A) ɢɡ n. Ɉɫɬɚɥɶɧɵɟ n m(A) ɢɫɯɨɞɨɜ ɛɥɚɝɨɩɪɢɹɬɧɵ ɩɪɨɬɢɜɨɩɨɥɨɠɧɨɦɭ ɫɨɛɵɬɢɸ, ɩɨɫɤɨɥɶɤɭ ɫɨɛɵɬɢɹ A ɢ ºA ɧɟɫɨɜɦɟɫɬɧɵ ɢ ɨɛɪɚɡɭɸɬ ɩɨɥɧɵɣ ɧɚɛɨɪ: AuºA , ɢ m(AuºA) 0. Ɂɧɚɱɢɬ, ɩɨ ɨɩɪɟɞɟɥɟɧɢɸ ɜɟɪɨɹɬɧɨɫɬɶ ɫɨɛɵɬɢɹ ºA ɟɫɬɶ
102

P(ºA) |
n m(A) |
1 P(A). |
|
n |
|
||
|
|
|
|
5. ȼɟɪɨɹɬɧɨɫɬɶ |
ɫɭɦɦɵ |
ɩ ɪ ɨ ɢ ɡ ɜ ɨ ɥ ɶ ɧ ɵ ɯ |
ɫɨɛɵɬɢɣ A B ɜɵ- |
ɱɢɫɥɹɟɬɫɹ ɬɚɤ: |
|
|
|
P(A B) P(A) P(B) P(AuB). |
(7.11) |
||
Ʉɨɝɞɚ AuBz, ɜ ɫɨɫɬɚɜɟ ɫɨɛɵɬɢɹ A ɢɦɟɟɬɫɹ m(AuB) ɢɫɯɨɞɨɜ, ɨɬɧɨɫɹɳɢɯɫɹ ɤ ɫɨɛɵɬɢɸ AuB. ɋɬɨɥɶɤɨ ɠɟ ɬɚɤɢɯ ɢɫɯɨɞɨɜ ɢɦɟɟɬɫɹ ɢ ɜ ɫɨɫɬɚɜɟ ɫɨɛɵɬɢɹ B. ɉɨɷɬɨɦɭ ɫɭɦɦɚ m(A) m(B) ɜɤɥɸɱɚɟɬ ɜ ɫɟɛɹ ɫɥɚɝɚɟɦɨɟ m(AuB) ɞɜɚɠɞɵ. ɇɨ ɜ ɫɨɫɬɚɜ ɫɨɛɵɬɢɹ A B ɤɚɠɞɵɣ ɢɡ ɢɫɯɨɞɨɜ, ɨɬɧɨɫɹɳɢɯɫɹ ɤ ɫɨɛɵɬɢɸ AuB, ɞɨɥɠɟɧ ɜɯɨɞɢɬɶ ɥɢɲɶ ɨɞɢɧ ɪɚɡ. ɉɨɷɬɨɦɭ ɱɢɫɥɨ m(A B) ɫɨɞɟɪɠɢɬ ɜ ɫɟɛɟ ɬɨɥɶɤɨ ɨɞɧɨ ɱɢɫɥɨ m(AuB), ɚ ɧɟ ɞɜɚ. Ɂɧɚɱɢɬ,
m(A B) m(A) m(B) m(AuB).
Ɉɬɫɸɞɚ ɩɨ ɨɩɪɟɞɟɥɟɧɢɸ ɩɨɥɭɱɚɟɦ ɮɨɪɦɭɥɭ (7.11), ɤɨɬɨɪɭɸ ɧɚɡɵɜɚɸɬ ɮɨɪɦɭɥɨɣ (ɩɪɚɜɢɥɨɦ) ɫɥɨɠɟɧɢɹ ɜɟɪɨɹɬɧɨɫɬɟɣ.
ȼɟɪɨɹɬɧɨɫɬɶ ɫɭɦɦɵ ɧɟɫɨɜɦɟɫɬɧɵɯ ɫɨɛɵɬɢɣ A B ɪɚɜɧɚ
P(A B) P(A) P(B). |
(7.12) |
ȿɫɥɢ ɫɨɛɵɬɢɹ A ɢ B ɧɟɫɨɜɦɟɫɬɧɵ, ɬɨ AuB , ɢ m(AuB) 0. Ɂɧɚɱɢɬ, P(AuB) 0, ɢ ɮɨɪɦɭɥɚ (7.11) ɩɪɟɨɛɪɚɡɭɟɬɫɹ ɤ ɮɨɪɦɭɥɟ (7.12).
ɉɪɚɜɢɥɨ (7.12) ɩɨ ɢɧɞɭɤɰɢɢ ɪɚɫɩɪɨɫɬɪɚɧɹɟɬɫɹ ɧɚ ɩɪɨɢɡɜɨɥɶɧɨɟ ɱɢɫɥɨ ɩɨɩɚɪɧɨ ɧɟɡɚɜɢɫɢɦɵɯ ɫɨɛɵɬɢɣ Ak, k 1,K :
§ K |
· |
K |
P¨¨¦Ak ¸¸ ¦P Ak . |
||
©k 1 |
¹ |
k 1 |
ɉɨɩɚɪɧɨ ɧɟɫɨɜɦɟɫɬɧɵɟ ɫɨɛɵɬɢɹ Ai ɢ Aj – ɷɬɨ ɬɟ ɫɨɛɵɬɢɹ, ɞɥɹ ɤɨ-
ɬɨɪɵɯ ɜɵɩɨɥɧɹɟɬɫɹ ɭɫɥɨɜɢɟ AiuAj ɩɪɢ ɥɸɛɵɯ izj, i,j 1,K . ɉɭɫɬɶ ɫɨɛɵɬɢɹ A, B,..., C ɨɛɪɚɡɭɸɬ ɩɨɥɧɵɣ ɧɚɛɨɪ. Ɍɨɝɞɚ
P(A) P(B) P(C) 1.
ȼ ɫɚɦɨɦ ɞɟɥɟ, ɩɨ ɨɩɪɟɞɟɥɟɧɢɸ A B C :, ɚ P(:) 1.
7.4. Теорема умножения вероятностей
ȼɜɟɞɟɦ ɫɧɚɱɚɥɚ ɜɚɠɧɵɟ ɩɨɧɹɬɢɹ ɨ ɧɟɡɚɜɢɫɢɦɵɯ ɢ ɡɚɜɢɫɢɦɵɯ ɫɨɛɵɬɢɹɯ.
ɋɨɛɵɬɢɟ B ɧɚɡɵɜɚɟɬɫɹ ɧɟɡɚɜɢɫɢɦɵɦ ɨɬ ɫɨɛɵɬɢɹ A, ɟɫɥɢ ɜɟɪɨɹɬɧɨɫɬɶ ɧɚɫɬɭɩɥɟɧɢɹ B ɧɟ ɢɡɦɟɧɹɟɬɫɹ ɨɬ ɬɨɝɨ, ɩɪɨɢɡɨɲɥɨ A ɢɥɢ ɧɟɬ.
103

ɋɨɛɵɬɢɟ D ɧɚɡɵɜɚɟɬɫɹ ɡɚɜɢɫɢɦɵɦ ɨɬ ɫɨɛɵɬɢɹ C, ɟɫɥɢ ɜɟɪɨɹɬɧɨɫɬɶ ɧɚɫɬɭɩɥɟɧɢɹ D ɢɦɟɟɬ ɨɞɧɨ ɡɧɚɱɟɧɢɟ, ɤɨɝɞɚ C ɧɟ ɩɪɨɢɡɨɲɥɨ, ɢ ɷɬɚ ɜɟɪɨɹɬɧɨɫɬɶ ɢɦɟɟɬ ɞɪɭɝɨɟ ɡɧɚɱɟɧɢɟ ɬɨɝɞɚ, ɤɨɝɞɚ C ɧɚɫɬɭɩɢɥɨ.
Ɏɚɤɬ ɧɟɡɚɜɢɫɢɦɨɫɬɢ ɫɥɭɱɚɣɧɵɯ ɫɨɛɵɬɢɣ ɭɫɬɚɧɚɜɥɢɜɚɸɬ ɩɭɬɟɦ ɚɧɚɥɢɡɚ ɭɫɥɨɜɢɣ ɡɚɞɚɱɢ, ɢɫɫɥɟɞɨɜɚɧɢɹ ɦɨɞɟɥɢ ɫɥɭɱɚɣɧɨɝɨ ɷɤɫɩɟɪɢɦɟɧɬɚ.
ɉɪɨɜɟɞɟɦ ɞɜɚ ɫɥɭɱɚɣɧɵɯ ɷɤɫɩɟɪɢɦɟɧɬɚ.
1. ȼ ɭɪɧɟ ɞɜɚ ɛɟɥɵɯ ɲɚɪɚ ɢ ɨɞɢɧ ɱɟɪɧɵɣ. ɂɡ ɭɪɧɵ ɧɚɭɝɚɞ ɜɵɧɢɦɚɸɬ ɨɞɢɧ ɲɚɪ, ɮɢɤɫɢɪɭɸɬ ɟɝɨ ɰɜɟɬ ɢ ɜɨɡɜɪɚɳɚɸɬ ɲɚɪ ɜ ɭɪɧɭ. Ɋɚɫɫɦɚɬɪɢɜɚɸɬɫɹ ɞɜɚ ɫɨɛɵɬɢɹ:
Ȼ1 – ɩɨɹɜɥɟɧɢɟ ɛɟɥɨɝɨ ɲɚɪɚ ɜ ɩɟɪɜɨɣ ɩɨɩɵɬɤɟ, Ȼ2 – ɩɨɹɜɥɟɧɢɟ ɛɟɥɨɝɨ ɲɚɪɚ ɜɨ ɜɬɨɪɨɣ ɩɨɩɵɬɤɟ.
Ɉɱɟɜɢɞɧɨ, ɱɬɨ ɜɟɪɨɹɬɧɨɫɬɶ ɧɚɫɬɭɩɥɟɧɢɹ ɫɨɛɵɬɢɹ Ȼ2 ɪɚɜɧɚ 2 , ɢ 3
ɨɧɚ ɧɢɤɚɤ ɧɟ ɡɚɜɢɫɢɬ ɨɬ ɬɨɝɨ, ɩɪɨɢɡɨɲɥɨ ɫɨɛɵɬɢɟ Ȼ1 ɢɥɢ ɨɧɨ ɧɟ ɩɪɨɢɡɨɲɥɨ. Ɂɧɚɱɢɬ, ɜ ɷɬɨɦ ɫɥɭɱɚɣɧɨɦ ɷɤɫɩɟɪɢɦɟɧɬɟ ɫɨɛɵɬɢɟ Ȼ2 ɧɟ ɡɚɜɢɫɢɬ ɨɬ ɫɨɛɵɬɢɹ Ȼ1.
2. ȼ ɭɪɧɟ ɞɜɚ ɛɟɥɵɯ ɲɚɪɚ ɢ ɨɞɢɧ ɱɟɪɧɵɣ. ɂɡ ɭɪɧɵ ɧɚɭɝɚɞ ɜɵɧɢɦɚɸɬ ɨɞɢɧ ɲɚɪ, ɧɨ ɧɟ ɜɨɡɜɪɚɳɚɸɬ ɟɝɨ ɜ ɭɪɧɭ. Ɋɚɫɫɦɚɬɪɢɜɚɸɬɫɹ ɞɜɚ ɫɨɛɵɬɢɹ:
Ȼ1 – ɩɨɹɜɥɟɧɢɟ ɛɟɥɨɝɨ ɲɚɪɚ ɜ ɩɟɪɜɨɣ ɩɨɩɵɬɤɟ, Ȼ2 – ɩɨɹɜɥɟɧɢɟ ɛɟɥɨɝɨ ɲɚɪɚ ɜɨ ɜɬɨɪɨɣ ɩɨɩɵɬɤɟ.
Ɍɟɩɟɪɶ ɜɟɪɨɹɬɧɨɫɬɶ ɧɚɫɬɭɩɥɟɧɢɹ ɫɨɛɵɬɢɹ Ȼ2 ɫɭɳɟɫɬɜɟɧɧɨ ɡɚɜɢɫɢɬ ɨɬ ɬɨɝɨ, ɢɦɟɥɨ ɦɟɫɬɨ ɫɨɛɵɬɢɟ Ȼ1 ɢɥɢ ɧɟɬ. ȿɫɥɢ ɫɨɛɵɬɢɟ Ȼ1 (ɜɟɪɨ-
ɹɬɧɨɫɬɶ ɟɝɨ ɧɚɫɬɭɩɥɟɧɢɹ ɪɚɜɧɚ 2 ) ɩɪɨɢɡɨɲɥɨ, ɬɨ ɜɟɪɨɹɬɧɨɫɬɶ ɧɚɫɬɭ- 3
ɩɥɟɧɢɹ Ȼ2 ɪɚɜɧɚ 1 (ɜ ɭɪɧɟ ɨɫɬɚɥɢɫɶ ɨɞɢɧ ɛɟɥɵɣ ɲɚɪ ɢ ɨɞɢɧ ɱɟɪɧɵɣ). 2
ȿɫɥɢ ɠɟ ɫɨɛɵɬɢɟ Ȼ1 ɧɟ ɧɚɫɬɭɩɢɥɨ, ɬɨ ɜɟɪɨɹɬɧɨɫɬɶ ɫɨɛɵɬɢɹ Ȼ2 ɪɚɜɧɚ 1 (ɜ ɭɪɧɟ ɨɫɬɚɥɨɫɶ ɬɨɥɶɤɨ ɞɜɚ ɛɟɥɵɯ ɲɚɪɚ). Ɂɧɚɱɢɬ, ɜ ɷɬɨɦ ɫɥɭɱɚɣɧɨɦ ɷɤɫɩɟɪɢɦɟɧɬɟ ɫɨɛɵɬɢɟ Ȼ2 ɡɚɜɢɫɢɬ ɨɬ ɫɨɛɵɬɢɹ Ȼ1.
ȼɟɪɨɹɬɧɨɫɬɶ ɫɨɛɵɬɢɹ B, ɜɵɱɢɫɥɟɧɧɚɹ ɩɪɢ ɭɫɥɨɜɢɢ, ɱɬɨ ɢɦɟɥɨ ɦɟɫɬɨ ɫɨɛɵɬɢɟ A, ɧɚɡɵɜɚɟɬɫɹ ɭɫɥɨɜɧɨɣ ɜɟɪɨɹɬɧɨɫɬɶɸ ɫɨɛɵɬɢɹ B ɢ ɨɛɨɡɧɚɱɚɟɬɫɹ ɤɚɤ P(B°A).
ɋɮɨɪɦɭɥɢɪɭɟɦ ɬɟɨɪɟɦɭ ɭɦɧɨɠɟɧɢɹ ɜɟɪɨɹɬɧɨɫɬɟɣ.
ȼɟɪɨɹɬɧɨɫɬɶ ɩɪɨɢɡɜɟɞɟɧɢɹ ɫɨɛɵɬɢɣ AuB ɪɚɜɧɚ ɩɪɨɢɡɜɟɞɟɧɢɸ ɜɟɪɨɹɬɧɨɫɬɢ ɩɟɪɜɨɝɨ ɫɨɦɧɨɠɢɬɟɥɹ ɧɚ ɭɫɥɨɜ-
104

ɧɭɸ ɜɟɪɨɹɬɧɨɫɬɶ ɜɬɨɪɨɝɨ ɫɨɦɧɨɠɢɬɟɥɹ, ɜɵɱɢɫɥɟɧɧɭɸ ɩɪɢ ɭɫɥɨɜɢɢ, ɱɬɨ ɩɟɪɜɨɟ ɢɦɟɥɨ ɦɟɫɬɨ:
P(AuB) P(A)uP(B~A). |
(7.13) |
ɉɭɫɬɶ ɜ ɩɪɨɫɬɪɚɧɫɬɜɟ : (ɪɢɫ. 7.3) ɧɚɫɱɢɬɵɜɚɟɬɫɹ n ɢɫɯɨɞɨɜ. ɋɨɛɵɬɢɸ A ɛɥɚɝɨɩɪɢɹɬɧɵ m ɢɫɯɨɞɨɜ, ɫɨɛɵɬɢɸ B ɛɥɚɝɨɩɪɢɹɬɧɵ k ɢɫɯɨɞɨɜ. ɋɪɟɞɢ ɢɫɯɨɞɨɜ, ɛɥɚɝɨɩɪɢɹɬɧɵɯ ɫɨɛɵɬɢɸ A, ɫɭɳɟɫɬɜɭɸɬ ɢɫɯɨɞɵ, ɤɨɬɨɪɵɟ ɛɥɚɝɨɩɪɢɹɬɧɵ ɢ ɫɨɛɵɬɢɸ B. ɗɬɨ ɬɟ ɠɟ l ɢɫɯɨɞɨɜ, ɤɨɬɨɪɵɟ ɛɥɚɝɨɩɪɢɹɬɧɵ ɫɨɛɵɬɢɸ AuB (ɪɢɫ. 7.3). Ɍɨɝɞɚ
P(A) |
m |
, |
P(AuB) |
l |
. |
|
|
||||
|
n |
|
n |
||
ɍɫɥɨɜɧɭɸ ɜɟɪɨɹɬɧɨɫɬɶ P(B~A) ɜɵɱɢɫɥɹɟɦ, ɢɫɯɨɞɹ ɢɡ ɬɨɝɨ ɮɚɤɬɚ, ɱɬɨ ɫɨɛɵɬɢɟ A ɧɚɫɬɭɩɢɥɨ. ɂ ɟɫɥɢ A ɧɚɫɬɭɩɢɥɨ, ɬɨ ɢɫɯɨɞɵ, ɛɥɚɝɨɩɪɢɹɬɧɵɟ ɫɨɛɵɬɢɸ B, ɧɭɠɧɨ ɜɵɛɢɪɚɬɶ ɢɡ m ɢɫɯɨɞɨɜ, ɫɨɫɬɚɜɥɹɸɳɢɯ ɫɨɛɵɬɢɟ A. Ʉɚɤ ɜɢɞɢɦ (ɪɢɫ. 7.3), ɢɦɟɟɬɫɹ l ɬɚɤɢɯ ɢɫɯɨɞɨɜ. Ɂɧɚɱɢɬ, ɭɫɥɨɜɧɚɹ ɜɟɪɨɹɬɧɨɫɬɶ P(B~A) ɜɵɱɢɫɥɹɟɬɫɹɬɚɤ:
P(B~A) l . m
ɉɨɞɫɬɚɜɢɜ ɩɨɥɭɱɟɧɧɵɟ ɜɵɪɚɠɟɧɢɹ ɞɥɹ
P(AuB), P(A) ɢ P(B~A) ɜ ɮɨɪɦɭɥɭ (7.13), ɩɨɥɭ-
ɱɢɦ ɬɨɠɞɟɫɬɜɨ. ɗɬɨ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɬɟɨɪɟɦɚ ɭɦɧɨɠɟɧɢɹ ɜɟɪɨɹɬɧɨɫɬɟɣ ɞɨɤɚɡɚɧɚ.
n
:  m
m
A 






k
B 
l
AuB 
Ɋɢɫ. 7.3
Ɇɟɬɨɞɨɦ ɦɚɬɟɦɚɬɢɱɟɫɤɨɣ ɢɧɞɭɤɰɢɢ ɬɟɨɪɟɦɭ ɭɦɧɨɠɟɧɢɹ ɜɟɪɨɹɬɧɨɫɬɟɣ ɦɨɠɧɨ ɪɚɫɩɪɨɫɬɪɚɧɢɬɶ ɧɚ ɩɪɨɢɡɜɟɞɟɧɢɟ ɥɸɛɨɝɨ ɱɢɫɥɚ ɫɨɛɵɬɢɣ:
P(AuBuC) P(A)uP(B~A)uP(C~(AuB)),
P(AuBuCuD) P(A)uP(B~A)uP(C~(AuB))uP(D~(AuBuC)) ɢ ɬ.ɞ.
ɉɪɢɦɟɪ. ȼ ɭɪɧɟ ɥɟɠɚɬ ɬɪɢ ɛɟɥɵɯ, ɬɪɢ ɱɟɪɧɵɯ ɢ ɬɪɢ ɠɟɥɬɵɯ ɲɚɪɚ. ɇɚɭɝɚɞ ɜɵɧɢɦɚɸɬ ɨɞɢɧ ɡɚ ɞɪɭɝɢɦ ɬɪɢ. Ʉɚɤɨɜɚ ɜɟɪɨɹɬɧɨɫɬɶ ɬɨɝɨ, ɱɬɨ ɜɫɟ ɬɪɢ ɜɵɧɭɬɵɯ ɲɚɪɚ ɨɤɚɠɭɬɫɹ ɨɞɧɨɝɨ ɰɜɟɬɚ?
Ɋɟɲɟɧɢɟ. ɉɟɪɜɵɣ ɲɚɪ ɦɨɠɟɬ ɛɵɬɶ ɥɸɛɨɝɨ ɰɜɟɬɚ – ɫɨɛɵɬɢɟ ɐ1 (ɢ ɷɬɨ ɫɨɛɵɬɢɟ – ɞɨɫɬɨɜɟɪɧɨɟ). ɇɨ ɜɬɨɪɨɣ ɲɚɪ ɞɨɥɠɟɧ ɛɵɬɶ ɬɨɝɨ ɠɟ ɰɜɟɬɚ, ɱɬɨ ɢ ɩɟɪɜɵɣ – ɫɨɛɵɬɢɟ ɐ2. Ɍɪɟɬɢɣ ɲɚɪ ɞɨɥɠɟɧ ɛɵɬɶ ɬɨɝɨ ɠɟ ɰɜɟɬɚ, ɱɬɨ ɢ ɞɜɚ ɩɟɪɜɵɯ – ɫɨɛɵɬɢɟ ɐ3. ɋɨɛɵɬɢɟ ɐ, ɫɨɫɬɨɹɳɟɟ ɜ ɬɨɦ, ɱɬɨ ɜɫɟ ɬɪɢ ɲɚɪɚ ɨɞɧɨɜɪɟɦɟɧɧɨ ɨɤɚɠɭɬɫɹ ɨɞɧɨɝɨ ɰɜɟɬɚ, ɫɭɬɶ ɩɪɨɢɡɜɟɞɟɧɢɟ ɬɪɟɯ ɧɚɡɜɚɧɧɵɯ: ɐ ɐ1uɐ2uɐ3. Ⱦɚɥɟɟ ɩɨ ɭɫɥɨɜɢɸ ɡɚɞɚɱɢ:
105
P(ɐ1) 1, P(ɐ2~ɐ1) |
2 |
, ɚ P(ɐ3~(ɐ1uɐ2)) |
1 |
. ɉɨɷɬɨɦɭ |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
||||
8 |
|
|
|
|
|
|
|
|
||
P(ɐ) P(ɐ1)uP(ɐ2~ɐ1)uP(ɐ3~(ɐ1uɐ2)) 1u |
2 |
u |
1 |
|
1 |
. |
||||
|
|
28 |
||||||||
|
|
|
8 |
7 |
|
|||||
ɋɥɟɞɫɬɜɢɟɦ ɢɡ ɬɟɨɪɟɦɵ ɭɦɧɨɠɟɧɢɹ ɜɟɪɨɹɬɧɨɫɬɟɣ ɛɭɞɟɬ ɬɚɤɨɟ ɭɬɜɟɪɠɞɟɧɢɟ.
ȿɫɥɢ ɫɨɛɵɬɢɟ B ɧɟ ɡɚɜɢɫɢɬ ɨɬ ɫɨɛɵɬɢɹ A, ɬɨ ɢ ɫɨɛɵɬɢɟ A ɧɟ ɡɚɜɢɫɢɬ ɨɬ ɫɨɛɵɬɢɹ B.
ɍɫɥɨɜɢɟ ɧɟɡɚɜɢɫɢɦɨɫɬɢ ɫɨɛɵɬɢɹ A (ɫɨɛɵɬɢɹ B) ɨɬ ɫɨɛɵɬɢɹ B (ɨɬ ɫɨɛɵɬɢɹ A) ɡɚɩɢɫɵɜɚɟɬɫɹ ɬɚɤ:
P(B°A) |
P(B), |
(7.14) |
P(A°B) |
P(A). |
(7.15) |
ɉɨɥɨɠɢɦ, ɱɬɨ (7.14) ɞɚɧɨ (ɫɨɛɵɬɢɟ B ɧɟ ɡɚɜɢɫɢɬ ɨɬ ɫɨɛɵɬɢɹ A) ɢ ɞɨɤɚɠɟɦ ɭɬɜɟɪɠɞɟɧɢɟ (7.15) – ɫɨɛɵɬɢɟ A ɧɟ ɡɚɜɢɫɢɬ ɨɬ ɫɨɛɵɬɢɹ B.
Ɂɚɩɢɲɟɦ ɮɨɪɦɭɥɭ ɭɦɧɨɠɟɧɢɹ ɜɟɪɨɹɬɧɨɫɬɟɣ ɞɥɹ ɫɨɛɵɬɢɣ BuA ɢ
AuB:
P(BuA) P(B)uP(A~B), P(AuB) P(A)uP(B~A).
ȼ ɫɢɥɭ ɬɨɠɞɟɫɬɜɚ 1’ ɚɥɝɟɛɪɵ ɫɨɛɵɬɢɣ (ɬɚɛɥ. 7.2) ɥɟɜɵɟ ɱɚɫɬɢ ɷɬɢɯ ɜɵɪɚɠɟɧɢɣ ɪɚɜɧɵ. Ɂɧɚɱɢɬ, ɪɚɜɧɵ ɢ ɢɯ ɩɪɚɜɵɟ ɱɚɫɬɢ:
P(B)uP(A~B) P(A)uP(B~A),
ɢɥɢ, ɫɨɝɥɚɫɧɨ (7.14),
P(B)uP(A~B) P(A)uP(B).
ɉɨɥɚɝɚɹ, ɱɬɨ P(B)z0, ɪɚɡɞɟɥɢɦ ɨɛɟ ɱɚɫɬɢ ɷɬɨɝɨ ɪɚɜɟɧɫɬɜɚ ɧɚ P(B):
P(A~B) P(A),
ɱɬɨ ɢ ɬɪɟɛɨɜɚɥɨɫɶ ɞɨɤɚɡɚɬɶ.
Ⱦɥɹ ɧɟɡɚɜɢɫɢɦɵɯ ɫɨɛɵɬɢɣ ɬɟɨɪɟɦɚ ɭɦɧɨɠɟɧɢɹ ɜɟɪɨɹɬɧɨɫɬɟɣ ɡɜɭɱɢɬ ɬɚɤ.
ȼɟɪɨɹɬɧɨɫɬɶ ɩɪɨɢɡɜɟɞɟɧɢɹ ɧɟɡɚɜɢɫɢɦɵɯ ɫɨɛɵɬɢɣ ɪɚɜɧɚ ɩɪɨɢɡɜɟɞɟɧɢɸ ɜɟɪɨɹɬɧɨɫɬɟɣ ɷɬɢɯ ɫɨɛɵɬɢɣ:
P(AuB) P(A)uP(B),
P(AuBuC) P(A)uP(B)uP(C),
P(AuBuCuD) P(A)uP(B)uP(C)uP(D).
ɉɪɢɦɟɪ. ȼɟɪɨɹɬɧɨɫɬɶ ɬɨɝɨ, ɱɬɨ ɫɬɭɞɟɧɬ ɂɦɹɪɟɤ ɫɞɚɫɬ ɷɤɡɚɦɟɧ ɩɨ Ƚɉ (ɝɪɚɠɞɚɧɫɤɨɦɭ ɩɪɚɜɭ), P(Ƚɉ) 0.7, ɚ ɜɟɪɨɹɬɧɨɫɬɶ ɫɞɚɱɢ ɢɦ ɷɤɡɚɦɟ-
106
ɧɚ ɩɨ ɋɋ (ɫɭɞɟɛɧɨɣ ɫɬɚɬɢɫɬɢɤɟ) P(ɋɋ) 0.8. ɇɚɣɬɢ ɜɟɪɨɹɬɧɨɫɬɶ ɬɨɝɨ, ɱɬɨ ɂɦɹɪɟɤ ɚ) ɫɞɚɫɬ ɨɛɚ ɷɤɡɚɦɟɧɚ, ɛ) ɨɛɚ ɷɤɡɚɦɟɧɚ ɧɟ ɫɞɚɫɬ.
Ɋɟɲɟɧɢɟ.
ɚ) ɋɨɛɵɬɢɟ «ɫɞɚɧɵ ɨɛɚ ɷɤɡɚɦɟɧɚ» ɫɭɬɶ Ƚɉuɋɋ. ɋɨɛɵɬɢɹ Ƚɉ ɢ ɋɋ ɮɢɡɢɱɟɫɤɢ ɧɟɡɚɜɢɫɢɦɵ. ɉɨɷɬɨɦɭ
P(Ƚɉuɋɋ) P(Ƚɉ)uP(ɋɋ) 0.7u0.8 0.56.
ɛ) ȿɫɥɢ ɫɨɛɵɬɢɹ Ƚɉ ɢ ɋɋ ɧɟɡɚɜɢɫɢɦɵ, ɬɨ ɧɟɡɚɜɢɫɢɦɵ ɢ ɩɪɨɬɢɜɨɩɨɥɨɠɧɵɟ ɫɨɛɵɬɢɹ ºȽɉ ɢ ºɋɋ. ȼɟɪɨɹɬɧɨɫɬɢ ɷɬɢɯ ɫɨɛɵɬɢɣ ɜɵɱɢɫɥɹɸɬɫɹ ɩɨɮɨɪɦɭɥɟ (7.10):
P(ºȽɉ) 1 P(Ƚɉ) 0.3, P(ºɋɋ) 1 P(ɋɋ) 0.2.
ɋɨɛɵɬɢɟ «ɨɛɚ ɷɤɡɚɦɟɧɚ ɧɟ ɫɞɚɧɵ» — ɷɬɨ ºȽɉuºɋɋ. Ɂɧɚɱɢɬ,
P(ºȽɉuºɋɋ) (1 P(Ƚɉ))u(1 P(ɋɋ)) 0.3u0.2 0.06.
7.5. Основные формулы теории вероятностей
Ɏɨɪɦɭɥɚ ɩɨɥɧɨɣ ɜɟɪɨɹɬɧɨɫɬɢ. Ⱦɚɧɧɚɹ ɮɨɪɦɭɥɚ ɜɵɬɟɤɚɟɬ ɢɡ ɡɚɤɨɧɨɜ ɫɥɨɠɟɧɢɹ ɢ ɭɦɧɨɠɟɧɢɹ ɜɟɪɨɹɬɧɨɫɬɟɣ. ɉɭɫɬɶ ɧɟɤɨɬɨɪɨɟ ɫɨɛɵɬɢɟ A ɦɨɠɟɬ ɩɪɨɢɡɨɣɬɢ ɫɨɜɦɟɫɬɧɨ ɫ ɨɞɧɢɦ ɢɡ ɫɨɛɵɬɢɣ H1, H2,…, Hn, ɨɛɪɚɡɭɸɳɢɯ ɩɨɥɧɭɸ ɝɪɭɩɩɭ. ɗɬɢ ɫɨɛɵɬɢɹ ɧɚɡɵɜɚɸɬ ɝ ɢ ɩ ɨ ɬ ɟ ɡ ɚ ɦ ɢ , ɩɨɬɨɦɭ ɱɬɨ A ɩɪɨɢɫɯɨɞɢɬ ɜ ɬɨɦ ɩɪɟɞɩɨɥɨɠɟɧɢɢ, ɱɬɨ ɫɥɭɱɢɥɨɫɶ ɯɨɬɹ ɛɵ ɨɞɧɨ ɢɡ ɷɬɢɯ ɫɨɛɵɬɢɣ:
A H1uA H2uA HnuA.
ɉɨɫɤɨɥɶɤɭ ɝɢɩɨɬɟɡɵ H1, H2,…, Hn ɨɛɪɚɡɭɸɬ ɩɨɥɧɵɣ ɧɚɛɨɪ, ɨɧɢ ɩɨɩɚɪɧɨ ɧɟɫɨɜɦɟɫɬɧɵ. ɉɨɷɬɨɦɭ ɢ ɫɨɛɵɬɢɹ H1uA, H2uA, , HnuA ɩɨɩɚɪɧɨ ɧɟɫɨɜɦɟɫɬɧɵ. Ɂɧɚɱɢɬ, ɤ ɜɵɱɢɫɥɟɧɢɸ ɜɟɪɨɹɬɧɨɫɬɢ P(A) ɦɨɠɧɨ ɩɪɢɦɟɧɢɬɶ ɮɨɪɦɭɥɭ ɫɥɨɠɟɧɢɹ ɜɟɪɨɹɬɧɨɫɬɟɣ (7.12):
n
P(A) P(H1uA) P(H2uA) P(HnuA) ¦P(Hi u A) .
i 1
Ⱥ ɜɟɪɨɹɬɧɨɫɬɶ P(HiuA) ɩɪɨɢɡɜɟɞɟɧɢɹ ɫɨɛɵɬɢɣ HiuA ɜɵɱɢɫɥɹɟɬɫɹ ɩɨ ɮɨɪɦɭɥɟ (7.13):
P(HiuA) P(Hi)uP(A~Hi).
Ɍɨɝɞɚ
P(A) P(H1)uP(A~H1) P(H2)uP(A~H2) |
P(Hn)uP(A~Hn) |
n |
|
¦P(Hi )uP(A~Hi), |
(7.16) |
i 1 |
|
107

ɬɨ ɟɫɬɶ ɜɟɪɨɹɬɧɨɫɬɶ ɫɨɛɵɬɢɹ A ɜɵɱɢɫɥɹɟɬɫɹ ɤɚɤ ɫɭɦɦɚ ɩɪɨɢɡɜɟɞɟɧɢɣ ɜɟɪɨɹɬɧɨɫɬɢ ɤɚɠɞɨɣ ɝɢɩɨɬɟɡɵ ɧɚ ɭɫɥɨɜɧɭɸ ɜɟɪɨɹɬɧɨɫɬɶ ɫɨɛɵɬɢɹ A ɩɪɢ ɷɬɨɣ ɝɢɩɨɬɟɡɟ. Ɏɨɪɦɭɥɚ (7.16) ɢ ɧɨɫɢɬ ɧɚɡɜɚɧɢɟ ɮɨɪɦɭɥɵ ɩɨɥɧɨɣ ɜɟɪɨɹɬɧɨɫɬɢ.
ɉɪɢɦɟɪ. ȼ ɰɟɯɟ ɞɜɟ ɝɪɭɩɩɵ ɫɬɚɧɤɨɜ ɩɪɨɢɡɜɨɞɹɬ ɨɞɧɢ ɢ ɬɟ ɠɟ ɞɟɬɚɥɢ, ɤɨɬɨɪɵɟ ɜ ɩɪɨɢɡɜɨɥɶɧɨɦ ɩɨɪɹɞɤɟ ɨɬɩɪɚɜɥɹɸɬɫɹ ɧɚ ɫɤɥɚɞ. ɋɬɚɧɤɨɜ ɩɟɪɜɨɣ ɝɪɭɩɩɵ 4, ɢ ɨɧɢ ɞɚɸɬ 5% ɛɪɚɤɚ. ɋɬɚɧɤɨɜ ɜɬɨɪɨɣ ɝɪɭɩɩɵ 6, ɢ ɛɪɚɤɚ ɭ ɧɢɯ 10%. ɇɚɣɬɢ ɜɟɪɨɹɬɧɨɫɬɶ ɬɨɝɨ, ɱɬɨ ɧɚɭɝɚɞ ɜɡɹɬɚɹ ɫɨ ɫɤɥɚɞɚ ɞɟɬɚɥɶ ɨɤɚɠɟɬɫɹ ɛɪɚɤɨɜɚɧɧɨɣ.
Ɋɟɲɟɧɢɟ. ɋɨɛɵɬɢɟ A – ɞɟɬɚɥɶ ɛɪɚɤɨɜɚɧɧɚɹ. ȼɨɡɦɨɠɧɵ ɫɥɟɞɭɸɳɢɟ ɝɢɩɨɬɟɡɵ ɞɥɹ ɧɚɫɬɭɩɥɟɧɢɹ ɷɬɨɝɨ ɫɨɛɵɬɢɹ:
H1 – ɞɟɬɚɥɶ ɢɡɝɨɬɨɜɥɟɧɚ ɧɚ ɫɬɚɧɤɚɯ ɩɟɪɜɨɣ ɝɪɭɩɩɵ, ɢ ɜɟɪɨɹɬ-
ɧɨɫɬɶ ɷɬɨɣ ɝɢɩɨɬɟɡɵ P(H1) |
|
4 |
0.4; |
|
10 |
||||
|
|
|||
H2 – ɞɟɬɚɥɶ ɢɡɝɨɬɨɜɥɟɧɚ ɧɚ ɫɬɚɧɤɚɯ ɜɬɨɪɨɣ ɝɪɭɩɩɵ, ɢ ɜɟɪɨɹɬ- |
||||
ɧɨɫɬɶ ɷɬɨɣ ɝɢɩɨɬɟɡɵ P(H2) |
|
6 |
0.6. |
|
10 |
||||
|
|
|||
Ƚɢɩɨɬɟɡɵ ɨɛɪɚɡɭɸɬ ɩɨɥɧɭɸ ɝɪɭɩɩɭ ɫɨɛɵɬɢɣ. Ⱦɚɥɟɟ, ɫɨɛɵɬɢɟ A~Hi (i 1,2) – ɛɪɚɤɨɜɚɧɧɚɹ ɞɟɬɚɥɶ ɛɵɥɚ ɢɡɝɨɬɨɜɥɟɧɚ ɧɚ ɫɬɚɧɤɚɯ i-ɣ ɝɪɭɩɩɵ. ȼɟɪɨɹɬɧɨɫɬɶ ɷɬɨɝɨ ɫɨɛɵɬɢɹ ɫɜɹɡɚɧɚ ɫ ɩɪɨɰɟɧɬɨɦ ɛɪɚɤɚ ɧɚ ɫɬɚɧɤɚɯ i-ɣ ɝɪɭɩɩɵ: P(A~H1) 0.05, P(A~H2) 0.10. Ɉɱɟɜɢɞɧɨ, ɱɬɨ ɫɨɛɵɬɢɟ A ɩɪɨɢɡɨɲɥɨ, ɟɫɥɢ ɢɦɟɥɨ ɦɟɫɬɨ ɢɥɢ ɫɨɛɵɬɢɟ A~H1, ɢɥɢ ɫɨɛɵɬɢɟ A~H2, ɬɨ ɟɫɬɶ A A~H1 A~H2. Ɂɧɚɱɢɬ,
P(A) P(H1)uP(A~H1) P(H2)uP(A~H2) 0.4u0.05 0.6u0.10 0.08.
Ɏɨɪɦɭɥɚ Ȼɚɣɟɫɚ. ɋɧɚɱɚɥɚ ɜɟɪɧɟɦɫɹ ɤ ɬɨɥɶɤɨ ɱɬɨ ɪɚɫɫɦɨɬɪɟɧɧɨɦɭ ɩɪɢɦɟɪɭ ɢ ɞɨɩɨɥɧɢɦ ɟɝɨ ɬɚɤ. ɉɭɫɬɶ ɫɨɛɵɬɢɟ A ɧɚɫɬɭɩɢɥɨ, ɧɚɭɝɚɞ ɨɬɨɛɪɚɧɧɚɹ ɞɟɬɚɥɶ ɨɤɚɡɚɥɚɫɶ ɛɪɚɤɨɜɚɧɧɨɣ. ɋɩɪɚɲɢɜɚɟɬɫɹ, ɤɚɤɨɜɚ ɜɟɪɨɹɬɧɨɫɬɶ ɬɨɝɨ, ɱɬɨ ɷɬɚ ɞɟɬɚɥɶ ɢɡɝɨɬɨɜɥɟɧɚ ɧɚ ɫɬɚɧɤɚɯ i-ɣ ɝɪɭɩɩɵ, ɬɨ ɟɫɬɶ ɪɟɚɥɢɡɨɜɚɥɚɫɶ ɝɢɩɨɬɟɡɚ Hi?
Ɋɟɲɟɧɢɟ. ɉɨɧɹɬɧɨ, ɱɬɨ ɜ ɧɚɲɟɦ ɫɥɭɱɚɟ ɫɨɛɵɬɢɟ A ɩɪɨɢɫɯɨɞɢɬ ɨɞɧɨɜɪɟɦɟɧɧɨ ɫ ɫɨɛɵɬɢɟɦ Hi, ɬɨ ɟɫɬɶ ɢɦɟɟɬ ɦɟɫɬɨ ɫɨɛɵɬɢɟ HiuA ɢɥɢ, ɱɬɨ ɬɨ ɠɟ ɫɚɦɨɟ, AuHi. ɉɨ ɮɨɪɦɭɥɟ (7.13) ɞɥɹ ɷɬɢɯ ɫɨɛɵɬɢɣ ɢɦɟɟɦ:
P(HiuA) P(Hi)uP(A~Hi),
P(AuHi) P(A)uP(Hi~A).
Ʌɟɜɵɟ ɱɚɫɬɢ ɷɬɢɯ ɜɵɪɚɠɟɧɢɣ ɪɚɜɧɵ, ɪɚɜɧɵ ɢ ɢɯ ɩɪɚɜɵɟ ɱɚɫɬɢ: P(Hi)uP(A~Hi) P(A)uP(Hi~A).
Ɉɬɫɸɞɚ
108
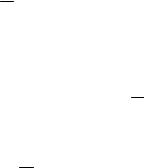
P(Hi~A) |
P(Hi )uP(A | Hi ) |
. |
(7.17) |
|
|||
|
P(A) |
|
|
ɇɚɩɨɦɧɢɦ, ɱɬɨ ɡɞɟɫɶ i 1,2. ȼɟɥɢɱɢɧɵ, ɜɯɨɞɹɳɢɟ ɜ ɮɨɪɦɭɥɭ (7.17),
ɧɚɦɢ |
ɭɠɟ ɨɩɪɟɞɟɥɟɧɵ: P(H1) |
0.4, P(H2) 0.6, P(A~H1) 0.05, |
P(A~H2) |
0.10, P(A) 0.08. Ɍɨɝɞɚ |
|
|
P(H1~A) 0.25, P(Hi~A) |
0.75. |
ȿɫɥɢ ɡɧɚɦɟɧɚɬɟɥɶ ɜ ɜɵɪɚɠɟɧɢɢ (7.17) ɜɵɱɢɫɥɢɬɶ ɩɨ ɮɨɪɦɭɥɟ (7.16),
ɩɨɥɭɱɢɦ ɮɨɪɦɭɥɭ Ȼɚɣɟɫɚ ɞɥɹ ɞɜɭɯ ɝɢɩɨɬɟɡ (i |
1,2): |
|
|
|
P(Hi )uP(A | Hi ) |
||
P(Hi~A) |
|
|
. |
|
|
||
P(H1)uP(A | H1) P(H2 )uP(A | H2 )
ȼ ɨɛɳɟɦ ɫɥɭɱɚɟ ɞɥɹ i 1,n ɨɧɚ ɡɚɩɢɫɵɜɚɟɬɫɹ ɬɚɤ:
P(Hi~A) |
|
P(Hi )uP(A | Hi ) |
. |
(7.18) |
|
n |
|||
|
¦P(Hi )uP(A | Hi ) |
|
|
|
|
i |
1 |
|
|
Ɏɨɪɦɭɥɚ Ȼɚɣɟɫɚ (ɢɥɢ ɮɨɪɦɭɥɚ ɝɢɩɨɬɟɡ) ɩɨɡɜɨɥɹɟɬ ɩɟɪɟɫɱɢɬɚɬɶ ɜɟɪɨɹɬɧɨɫɬɢ ɤɚɠɞɨɣ ɢɡ ɝɢɩɨɬɟɡ ɩɨɫɥɟ ɬɨɝɨ, ɤɚɤ ɧɚɫɬɭɩɢɥɨ ɨɛɭɫɥɨɜɥɟɧɧɨɟ ɢɦɢ ɫɨɛɵɬɢɟ. ȼ ɮɨɪɦɭɥɟ (7.18) ɢɫɯɨɞɧɵɟ ɜɟɪɨɹɬɧɨɫɬɢ ɝɢɩɨɬɟɡ P(Hi) ɧɚɡɵɜɚɸɬɫɹ ɚ ɩ ɪ ɢ ɨ ɪ ɧ ɵ ɦ ɢ (ɞɨɨɩɵɬɧɵɦɢ), ɚ ɢɫɤɨɦɵɟ ɜɟɪɨɹɬɧɨɫɬɢ P(Hi~A) – ɚ ɩ ɨ ɫ ɬ ɟ ɪ ɢ ɨ ɪ ɧ ɵ ɦ ɢ (ɩɨɫɥɟɨɩɵɬɧɵɦɢ).
ɉɪɢɦɟɪ. Ⱦɜɚ ɨɯɨɬɧɢɤɚ ɨɞɧɨɜɪɟɦɟɧɧɨ ɢ ɧɟɡɚɜɢɫɢɦɨ ɫɬɪɟɥɹɸɬ ɜ ɤɚɛɚɧɚ. ɂɡɜɟɫɬɧɨ, ɱɬɨ ɩɟɪɜɵɣ ɩɨɩɚɞɚɟɬ ɜ ɰɟɥɶ ɫ ɜɟɪɨɹɬɧɨɫɬɶɸ 0.8, ɚ ɜɬɨɪɨɣ – ɫ ɜɟɪɨɹɬɧɨɫɬɶɸ 0.5. Ʉɚɛɚɧ ɭɛɢɬ, ɢ ɜ ɧɟɦ ɨɛɧɚɪɭɠɟɧɚ ɨɞɧɚ ɩɭɥɹ. Ʉɚɤ ɫɩɪɚɜɟɞɥɢɜɨ ɪɚɡɞɟɥɢɬɶ ɬɪɨɮɟɣ?
Ɋɟɲɟɧɢɟ. Ɂɞɟɫɶ ɫɨɛɵɬɢɟ A – ɧɚɥɢɱɢɟ ɜ ɭɛɢɬɨɦ ɤɚɛɚɧɟ ɨɞɧɨɣ ɩɭɥɢ ɩɨɫɥɟ ɬɚɤɨɝɨ ɢɫɩɵɬɚɧɢɹ, ɤɚɤ ɞɜɚ ɨɞɧɨɜɪɟɦɟɧɧɵɯ ɢ ɧɟɡɚɜɢɫɢɦɵɯ ɜɵɫɬɪɟɥɚ. ȼ ɤɚɱɟɫɬɜɟ ɝɢɩɨɬɟɡ ɜɵɫɬɭɩɚɸɬ ɜɨɡɦɨɠɧɵɟ ɪɟɡɭɥɶɬɚɬɵ ɷɬɨɝɨ ɢɫɩɵɬɚɧɢɹ:
H00 – ɧɟ ɩɨɩɚɥ ɧɢ ɩɟɪɜɵɣ ɫɬɪɟɥɨɤ, ɧɢ ɜɬɨɪɨɣ, H10 – ɩɨɩɚɥ ɩɟɪɜɵɣ, ɧɟ ɩɨɩɚɥ ɜɬɨɪɨɣ,
H01 – ɧɟ ɩɨɩɚɥ ɩɟɪɜɵɣ, ɩɨɩɚɥ ɜɬɨɪɨɣ, H11 – ɩɨɩɚɥ ɢ ɩɟɪɜɵɣ, ɢ ɜɬɨɪɨɣ.
Ɉɛɨɡɧɚɱɢɦ ɷɥɟɦɟɧɬɚɪɧɵɟ ɫɨɛɵɬɢɹ ɜ ɞɚɧɧɨɦ ɢɫɩɵɬɚɧɢɢ: F – ɩɨɩɚɥ ɩɟɪɜɵɣ, T – ɩɨɩɚɥ ɜɬɨɪɨɣ. ɂɯ ɜɟɪɨɹɬɧɨɫɬɢ ɡɚɞɚɧɵ: P(F) 0.8, P(T) 0.5.
Ʉɚɠɞɚɹ ɢɡ ɝɢɩɨɬɟɡ – ɩɪɨɢɡɜɟɞɟɧɢɟ ɞɜɭɯ ɫɨɛɵɬɢɣ ɢɡ ɱɟɬɵɪɟɯ: {F,
ºF, T, ºT}:
H00 ºFuºT, H10 FuºT, |
H01 ºFuT, H11 FuT. |
109

ɂɯ ɚɩɪɢɨɪɧɵɟ ɜɟɪɨɹɬɧɨɫɬɢ ɬɚɤɨɜɵ:
P(H00) P(ºFuºT) 0.2u0.5 0.1;
P(H10) P(FuºT) 0.8u0.5 0.4;
P(H01) P(ºFuT) 0.2u0.5 0.1;
P(H11) P(FuT) 0.8u0.5 0.4.
Ɉɱɟɜɢɞɧɨ, ɱɬɨ
P(A~H00) 0; P(A~H10) 1; P(A~H01) 1; P(A~H11) 0.
ɋɩɪɚɜɟɞɥɢɜɵɦ ɛɭɞɟɬ ɞɟɥɢɬɶ ɞɨɛɵɱɭ ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɨ ɚɩɨɫɬɟɪɢɨɪɧɵɦ ɜɟɪɨɹɬɧɨɫɬɹɦ ɝɢɩɨɬɟɡ H10 ɢ H01,ɤɨɬɨɪɵɟ ɜɵɱɢɫɥɹɟɦ ɩɨ ɮɨɪɦɭɥɟ Ȼɚɣɟɫɚ:
P(H10~A) |
P(H10 )uP(A | H10 ) |
|
0.4 |
|
4 |
; |
|
P(H10 )uP(A | H10 ) P(H01 uP(A | H01) |
0.4 0.1 |
5 |
|||||
|
|
||||||
P(H01~A) |
P(H01)uP(A | H01) |
|
0.1 |
|
1 |
. |
|
P(H10 )uP(A | H10 ) P(H01 uP(A | H01) |
0.4 0.1 |
5 |
|||||
|
|
||||||
ɂɬɚɤ, ɩɟɪɜɨɦɭ ɨɯɨɬɧɢɤɭ ɞɨɫɬɚɧɟɬɫɹ |
4 |
, ɚ ɜɬɨɪɨɦɭ – |
1 |
ɬɪɨɮɟɹ. |
|
5 |
|||
5 |
|
|
||
Ɏɨɪɦɭɥɚ Ȼɟɪɧɭɥɥɢ. ɂ ɫɧɨɜɚ ɧɚɱɧɟɦ ɫ ɩɪɢɦɟɪɚ. ɉɨ ɦɢɲɟɧɢ ɩɪɨɢɡɜɨɞɢɬɫɹ ɬɪɢ ɧɟɡɚɜɢɫɢɦɵɯ ɜɵɫɬɪɟɥɚ. ȼɟɪɨɹɬɧɨɫɬɶ ɩɨɩɚɞɚɧɢɹ ɜ ɦɢɲɟɧɶ ɩɪɢ ɤɚɠɞɨɦ ɜɵɫɬɪɟɥɟ ɪɚɜɧɚ p. ɇɚɣɬɢ ɜɟɪɨɹɬɧɨɫɬɶ ɬɨɝɨ, ɱɬɨ ɩɪɢ ɷɬɢɯ ɬɪɟɯ ɜɵɫɬɪɟɥɚɯ ɩɨɥɭɱɢɬɫɹ ɪɨɜɧɨ ɞɜɚ ɩɨɩɚɞɚɧɢɹ.
Ɋɟɲɟɧɢɟ. Ɉɛɨɡɧɚɱɢɦ ɱɟɪɟɡ A1, A2, A3 ɩɨɩɚɞɚɧɢɹ ɩɪɢ ɩɟɪɜɨɦ, ɩɪɢ ɜɬɨɪɨɦ ɢ ɩɪɢ ɬɪɟɬɶɟɦ ɜɵɫɬɪɟɥɚɯ, ɚ ɱɟɪɟɡ ºA1, ºA2, ºA3 – ɩɪɨɦɚɯɢ ɩɪɢ ɩɟɪɜɨɦ, ɩɪɢ ɜɬɨɪɨɦ ɢ ɩɪɢ ɬɪɟɬɶɟɦ ɜɵɫɬɪɟɥɚɯ. ɉɪɢ ɷɬɨɦ ɜɟɪɨɹɬɧɨɫɬɶ ɩɨɩɚɞɚɧɢɹ ɩɪɢ ɥɸɛɨɦ ɢɡ ɜɵɫɬɪɟɥɨɜ ɪɚɜɧɚ P(Ai) p, ɚ ɜɟɪɨɹɬɧɨɫɬɶ ɩɪɨ-
ɦɚɯɚ ɩɪɢ ɥɸɛɨɦ ɢɡ ɜɵɫɬɪɟɥɨɜ – P(ºAi) 1 p q, (i 1,3 ). ɉɟɪɟɱɢɫɥɢɦ ɬɟ ɢɫɯɨɞɵ, ɜ ɤɨɬɨɪɵɯ ɧɚɛɥɸɞɚɸɬɫɹ ɞɜɚ ɩɨɩɚɞɚɧɢɹ:
A1uA2uºA3 – ɩɨɩɚɞɚɧɢɹ ɩɪɢ ɩɟɪɜɨɦ ɢ ɜɬɨɪɨɦ ɜɵɫɬɪɟɥɚɯ, ɩɪɨɦɚɯ ɩɪɢ ɬɪɟɬɶɟɦ,
A1uºA2uA3 – ɩɨɩɚɞɚɧɢɹ ɩɪɢ ɩɟɪɜɨɦ ɢ ɬɪɟɬɶɟɦ ɜɵɫɬɪɟɥɚɯ, ɩɪɨɦɚɯ ɩɪɢ ɜɬɨɪɨɦ,
ºA1uA2uA3 – ɩɪɨɦɚɯ ɩɪɢ ɩɟɪɜɨɦ ɜɵɫɬɪɟɥɟ, ɩɨɩɚɞɚɧɢɹ ɩɪɢ ɜɬɨɪɨɦ ɢ ɬɪɟɬɶɟɦ.
Ɉɱɟɜɢɞɧɨ, ɱɬɨ ɫɨɛɵɬɢɟ «ɪɨɜɧɨ ɞɜɚ ɩɨɩɚɞɚɧɢɹ ɩɪɢ ɬɪɟɯ ɜɵɫɬɪɟɥɚɯ» — ɷɬɨ ɫɭɦɦɚ ɩɟɪɟɱɢɫɥɟɧɧɵɯ ɢɫɯɨɞɨɜ:
A1uA2uºA3 A1uºA2uA3 ºA1uA2uA3.
ɋɥɚɝɚɟɦɵɟ ɜ ɷɬɨɣ ɫɭɦɦɟ – ɫɨɛɵɬɢɹ ɧɟɫɨɜɦɟɫɬɧɵɟ, ɚ ɫɨɦɧɨɠɢɬɟɥɢ ɜ ɤɚɠɞɨɦ ɢɡ ɧɢɯ – ɫɨɛɵɬɢɹ ɧɟɡɚɜɢɫɢɦɵɟ. Ɉɛɨɡɧɚɱɢɦ ɢɫɤɨɦɭɸ ɜɟɪɨɹɬ-
110
