4.2. Положительные обратносимметрические матрицы, их собственные векторы и значения.

Часто экспертам предлагают осуществить попарное сравнение nобъектов, путём приписывания каждому из них некоторого положительного числа (оценки объектов в заданной шкале измерения). В результате получается матрица попарных сравнений, из которых в дальнейшем надо построить «вектор приоритетов», т.е. фактически выстроить в данной шкале эти объекты по убыванию их значимости с точки зрения эксперта. Эта задача решается путём использования свойств специального вида матриц (положительных обратносимметрических).

Квадратная матрица называетсяположительной обратносимметрической матрицей (ПО-матрица), если её элементы удовлетворяют следующим двум соотношениям:

1. для любых i,j: а_ij>0

2. для любых i,j:.

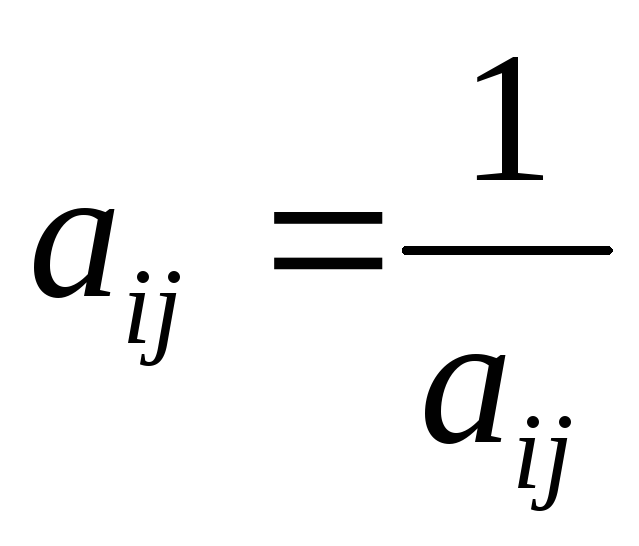Из определения ПО-матрицы следует, что все её диагональные элементы равны единице.

ПО-матрица называется согласованной, если для любыхi,j,k:.

Пример:Согласованная ПО-матрица

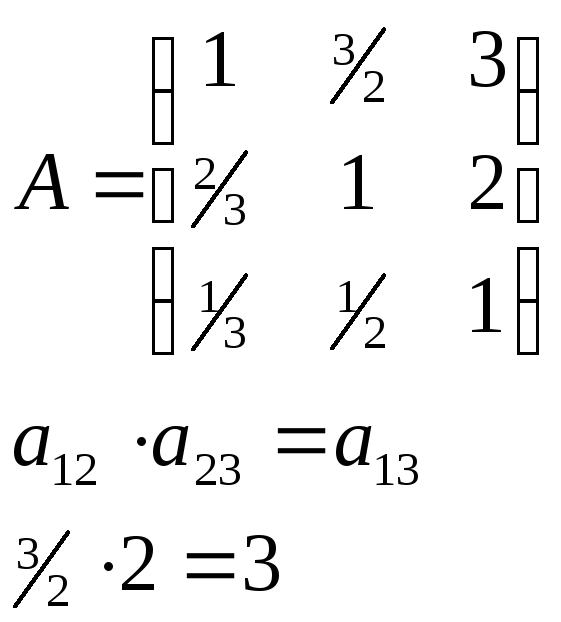
Теорема Перрона(существование и единственность главного собственного вектора и главного собственного значения).

Пусть дана положительная матрица А, тогда:

1. матрица А имеет действительное, положительное собственное значение 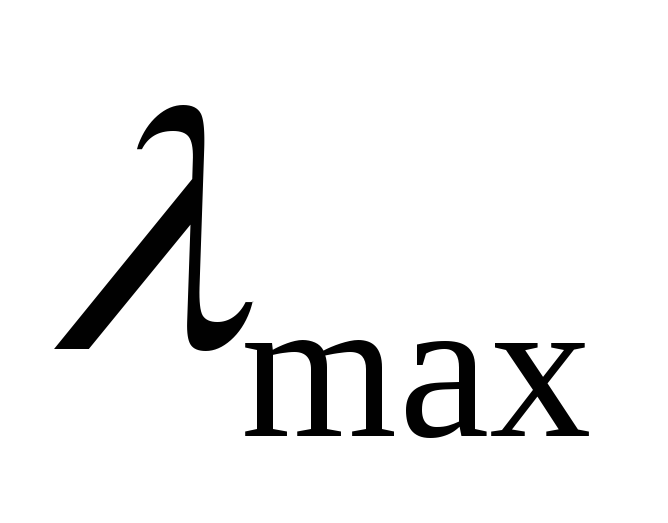(главное собственное значение), которое по модулю строго больше любого другого собственного значения.

2. собственный вектор матрицы А, соответствующий собственному значению 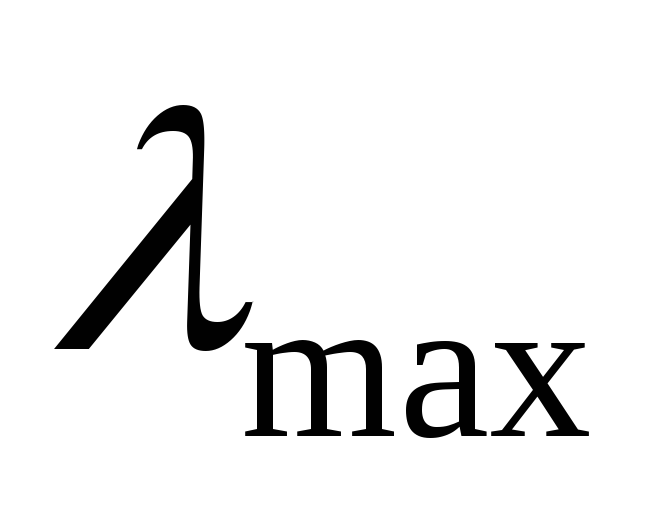(главный собственный вектор), имеет положительные компоненты и, с точностью до постоянного множителя, единственен.

Некоторые оценки .

1. 

2. 

Теорема (необходимое и достаточное условие согласованности ПО-матрицы):

ПО-матрица согласована тогда и только тогда, когда . Т.о. признак хорошей согласованности положительной обратносимметрической матрицы является близость её главного собственного значения к своей нижней границе.

Оценка главного собственного вектора положительной матрицы.

Теорема: Для положительной матрицы А: 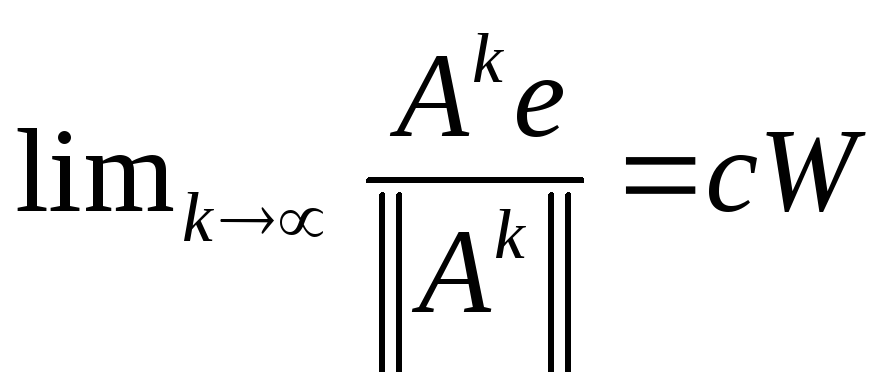, где

,

с – константа;

W– главный собственный вектор.

Замечания:

1. Можно показать, что для любой квадратной матрицы 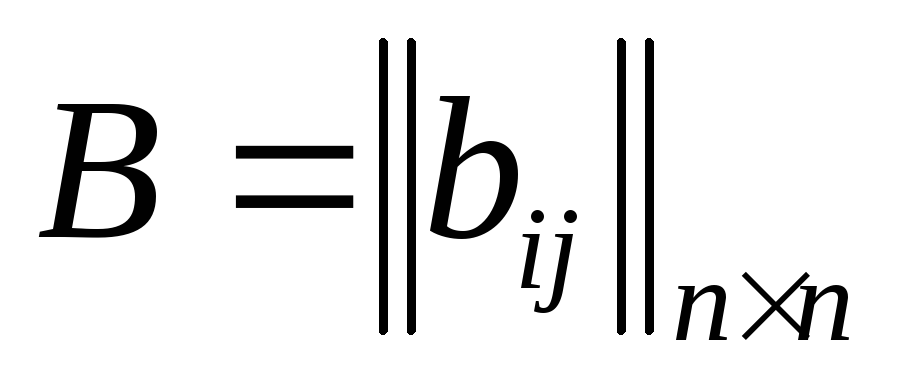выражение

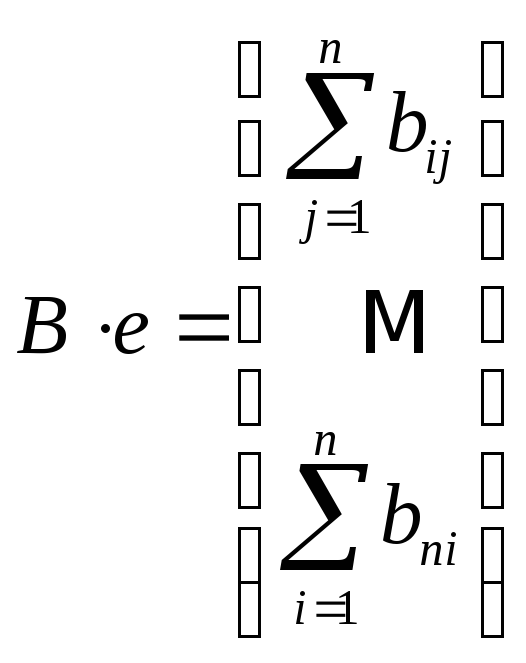2. - это вектор-столбец, у которого каждый элемент есть сумма элементов соответствующей строки матрицы В.

Т.о. теорема утверждает, что нормализованные строчные суммы степеней положительной матрицы в пределе дают искомый собственный вектор.

поэтому краткий вычислительный способ вычисления главного собственного вектора матрицы состоит в возведении матрицы в степени, каждая из которых представляет собой квадрат предыдущих. Далее вычисляются и нормализуются строчные суммы этих степеней. вычисления прекращаются, когда разность между этими нормализованными суммами (в двух последовательных итерациях) станет меньше заранее заданной величины точности вычислений.

Пример:

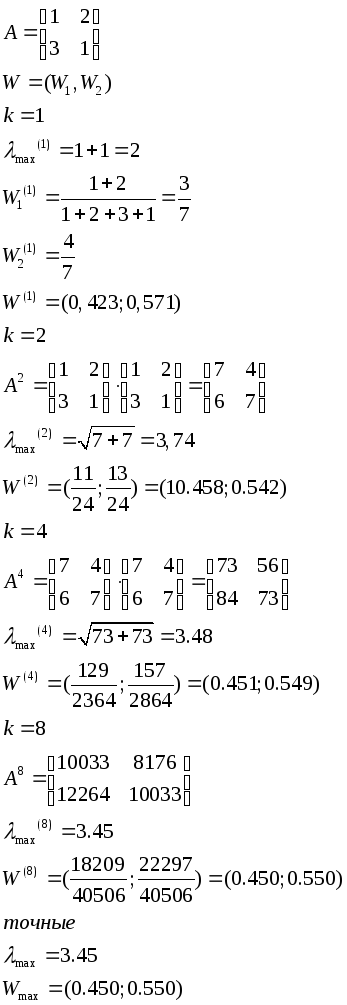
§5. Вычисление вектора приоритетов и оценка согласованности суждений эксперта при попарном сравнении объекта.

Допустим эксперту предложено путем попарных сравнений n- объектов (О₁ О₂...О_n) установить для каждой пары в шкале отношений какой из них лучше и во сколько раз.

O_i =a_ij *O_j. При этом если эксперт уже остановился на каком-то значении а_ijестественно потребовать чтобы(1) Таким образом матрица составленная из суждений эксперта будет положительной обратно симметрической. Если суждения эксперта совершенны (идеальны), т.е. если он:

• правильно понял свою задачу

• правильно выбрал шкалу измерения

• имеет твердое мнение о сравнительной важности объектов( не меняет его по ходу сравнения)

• имеет опыт работы в качестве эксперта и т.п.

то естественно ожидать, что для всех i,j,kбудет выполнятьсяa_ik =a_ij *a_jk (2)

Тем самым матрица А=||а_ij|| будет ещё и согласованной. Эти случаи (1) и (2) будут иметь место, если объекты могут быть хотя бы чисто теоретически взвешены на каких-то гипотетических весах, т.е. если эксперты мысленно приписывают каждому объекту его вес (W_i), а на бумаге сравнительная оценка пары объектовO_i иO_j уже имеет вид:

(3) И действительнои соотношение (2) выполняется.

Кроме того, 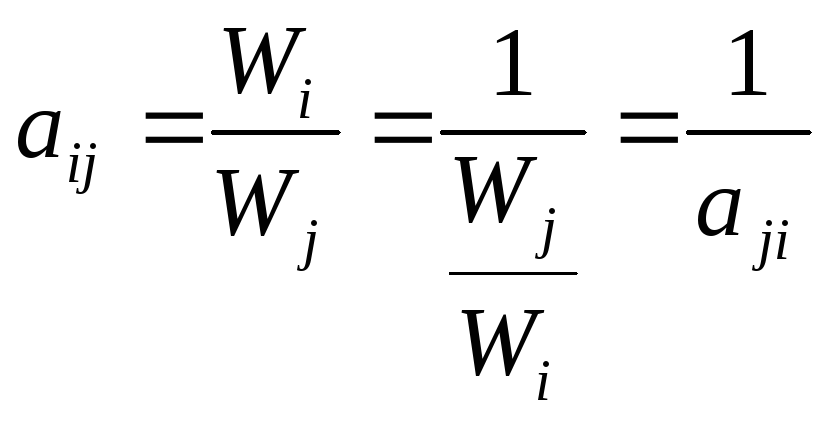и выполняется соотношение (1). Таким образом если бы нам удалось каким-то путём числено оценить векторW=(W₁,W₂,…,W_n), то это означало бы что мы в некоторой числовой шкале оценили относительную важность объектов О₁ , О₂...О_n. Этот векторW=(W₁,W₂,…,W_n) поэтому называетсявектором приоритетов. Покажем, что вектор приоритетов совпадает с главным собственным вектором положительной обратно симметрической согласованной матрицы парных сравнений.

Просуммируем левую и правую части поjполучим

В матричной формеA*W=n*W(4)

Из теории матриц можно заключить что Wэто собственный вектор матрицы А с собственным значением равнымn. Следовательно для нашей ПО-матрицы а_ii =1.

Если имеет место формула (4) и с учётом оценки λ_max ≥nвытекает что все собственные значения равны 0 кроме одного равногоn, значит λ_max =n. Из теории матриц известно, что собственные значения ПО-матрицы непрерывно зависят от её элементов, т.е. малым изменениямa_ij соответствуют малые изменения λ_i .

Следовательно, при малых изменениях a_ij , λ_max остаётся близким кn, а остальные λ_i к нулю. Хотя на практике уравнение (4) выполняться не будет. Для нахождения по матрице парных сравнений (А) векторов приоритетов (W) решают уравнениеA*W= λ_max *W(5) относительно вектораW.

Перейдем теперь к вопросу об оценке согласованности суждений эксперта при заполнении им матрицы парных сравнений.

Практически эту оценку строят следующим образом:

1. Вычисляют λ_max.

2. Вычисляют индекс согласованности 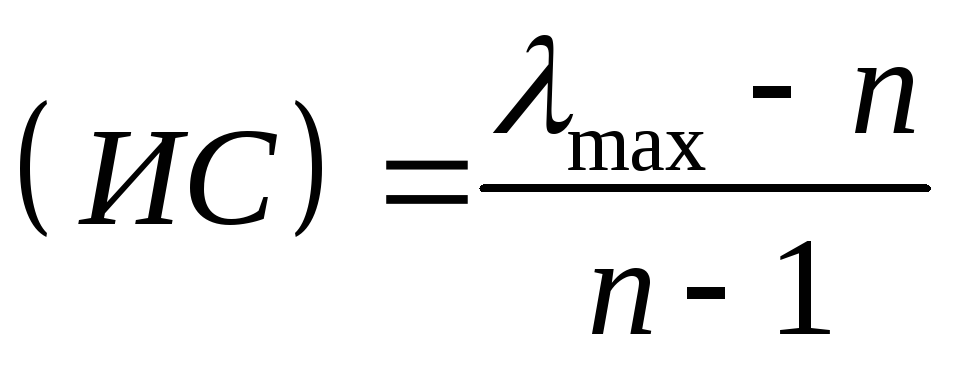(6)

3. Из специальных таблиц берут величину случайного индекса (СИ), соответствующего данному n.

4. Вычисляют отношение согласованности 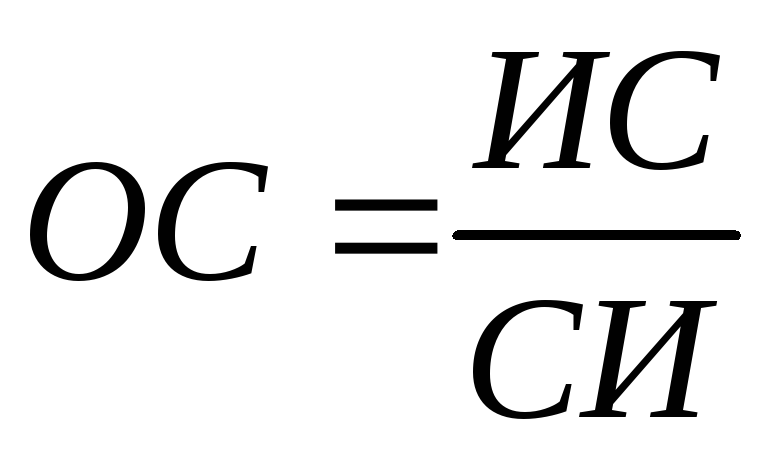(7)

Если ОС ≤ 0,1,то согласованность считается приемлемой, в противном случае матрица считается несогласованной и выясняются причины несогласованности.

Таблица СИ для некоторых n:

Примечание:

Были взяты несколько сотен положительных квадратных матриц заполненных случайным образом, для каждой из этих матриц вычислялся ИС, и результаты усредняли. Это среднее значение и назвали СИ. Таким образом, формула (7) отражает меру того во сколько раз суждения эксперта лучше согласовано по сравнению с методом “случайного тыка”, а результат у эксперта должен быть на порядок лучше.

Пример: n=3

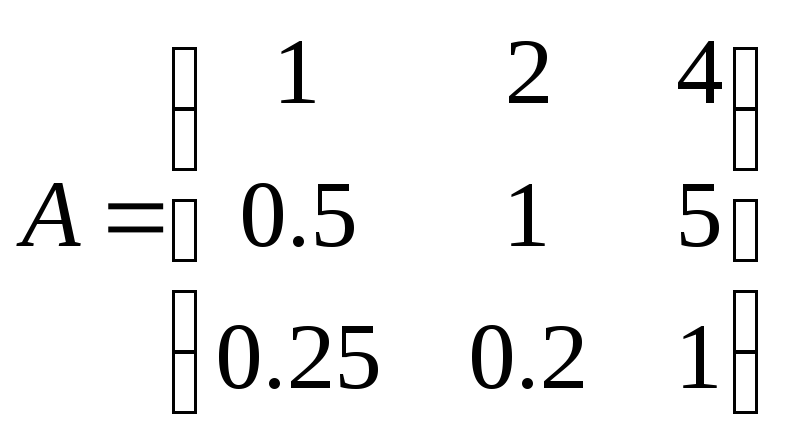;a₁₂ *a₂₃ ≠a₁₃ ; 2*5≠4 (матрица несогласованная)

1. λ_max = 3.094

2. 

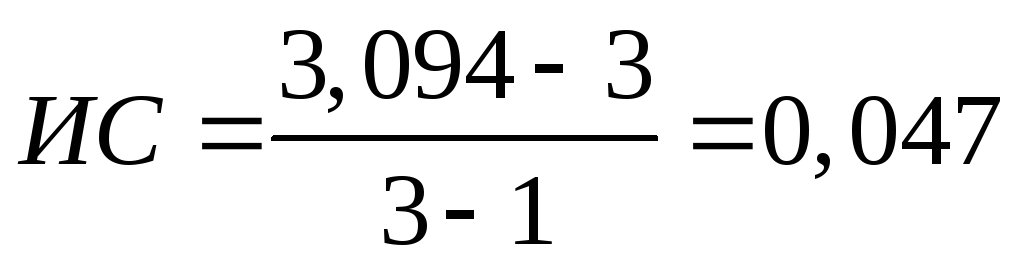
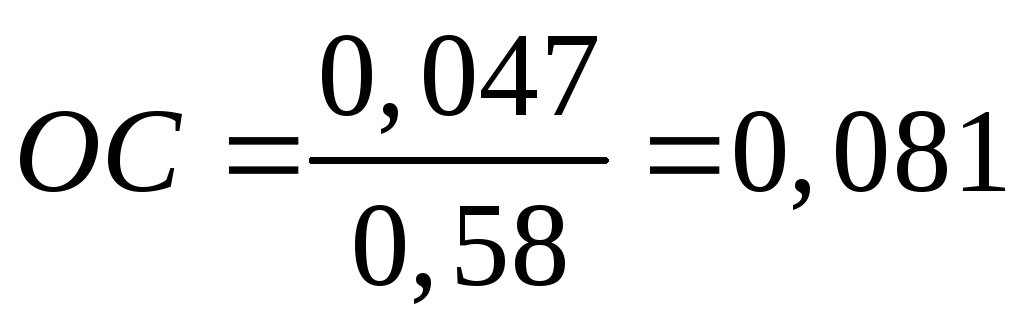3. <0.1 Матрица согласована удовлетворительно.