
-
Основні теореми про границі.
При обчисленні границь користуються наступними теоремами:
-
Функція
 не може мати більше однієї границі.
не може мати більше однієї границі. -
Якщо кожна з функцій
 та
та
 має скінченну границю при
має скінченну границю при
 ,
то сума, різниця і добуток цих функцій
також мають границю, причому:
,
то сума, різниця і добуток цих функцій
також мають границю, причому:
![]() ,
(7)
,
(7)
![]() .
(8)
.
(8)
Якщо
![]() ,
то і частка цих функцій
,
то і частка цих функцій
![]() також має границю, причому
також має границю, причому
 (9).
(9).
Наслідки!
Якщо кожний доданок алгебраїчної суми
функцій має границю при
![]() ,
то границя суми існує і дорівнює
алгебраїчній сумі границь доданків.
,
то границя суми існує і дорівнює
алгебраїчній сумі границь доданків.
![]() (10)
(10)
-
Сталий множник можна винести за знак границі:
![]() (11)
(11)
-
Якщо
 і
і
 – натуральне число, то
– натуральне число, то
 (12);
(12);
 (13)
(13) -
Границя сталої є сама стала
 (14)
(14)
Приклад. 2.
Знайти:
а)
![]() ;
б)
;
б)

Розв’язання
а) (7), (10), (11), (12) :

б) (9), (10), (11), (12):

-
Розкриття деяких невизначеностей
Нехай
треба обчислити границю відношення
многочленів
 .
.
Можливі
випадки: а)
![]() – скінченне число; б)
– скінченне число; б)
![]() .
.
У
випадку а) треба під знаком границі
замість х підставити
![]() в чисельник і знаменник .
в чисельник і знаменник .
Якщо
під знаком границі одержимо стале число
А або дріб виду
![]() чи
чи
![]() ,
то границею буде, відповідно А,
,
то границею буде, відповідно А,
![]() ,
чи 0..
,
чи 0..
Якщо
під знаком границі одержимо невизначеність
виду
![]() ,
то треба чисельник і знаменник розкласти
на множники, скоротити дріб, а потім
обчислити границю.
,
то треба чисельник і знаменник розкласти
на множники, скоротити дріб, а потім
обчислити границю.
У
випадку б) треба під знаком границі
поділити чисельник і знаменник на
![]() ,
де
,
де
![]() – найбільше з чисел
– найбільше з чисел
![]() і
і
![]() ,
і обчислити границю одержаного виразу.
,
і обчислити границю одержаного виразу.
При
цьому: якщо
![]() ,
то границею буде
,
то границею буде
![]() ;
;
при
![]() границею буде
границею буде
![]() або
або
![]() залежно від знака
залежно від знака
![]() ;
;
при
![]() границя буде дорівнювати 0.
границя буде дорівнювати 0.
Якщо
треба обчислити границю відношення
ірраціональних виразів, яке при
![]() приймає вигляд
приймає вигляд
![]() ,
то для розкриття невизначеності треба:
,
то для розкриття невизначеності треба:
-
чисельник і знаменник домножити на вираз, спряжений до ірраціонального виразу чисельника, або знаменника, або і чисельника і знаменника;
-
розкласти на множники чисельник і знаменник, спростити вираз і перейти до границі.
Приклад 3.
Знайти:
а)
 ;
б)
;
б)

Розв’язання:
а)
 ;
;
б)

-
Деякі важливі границі.
а)
Перша важлива границя
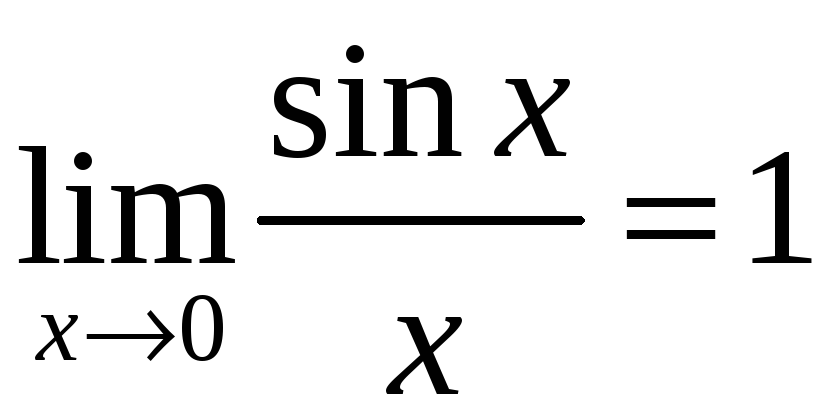 (14)
(14)
б)
Друга важлива границя
 (15.1)
(15.1)
 (15.2),
(15.2),
 (15.3)
(15.3)
 (15.4).
(15.4).
Примітка.
Якщо існує
![]() ,
то при сталому
,
то при сталому
![]() має місце рівність
має місце рівність
![]() .
(16).
.
(16).
Приклад
4. Знайти: а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)
 д)
д)
 .
.
Розв’язання
а)
 ;
;
б)
 ;
;
в)
 ;
;
г)


д)


-
Неперервність та розриви функції
Озн.1.
Функція
![]() називається неперервною при
називається неперервною при
![]() ,
якщо:
,
якщо:
1)
![]() визначена
при
визначена
при
![]() і в деякому околі
і в деякому околі
![]() ;
;
2) існує
скінченна границя
![]() ;
;
3)
![]() ,
тобто
,
тобто
![]() ;
;
Якщо
при
![]() хоч одна з умов 1-3 не виконується, то
кажуть, що функція
хоч одна з умов 1-3 не виконується, то
кажуть, що функція
![]() в точці
в точці
![]() має розрив, а точку
має розрив, а точку
![]() називають точкою розриву.
називають точкою розриву.
Якщо
функція
![]() визначена при
визначена при
![]() і
і
![]() ,
то кажуть, що
,
то кажуть, що
![]() неперервна в точці
неперервна в точці
![]() справа.
справа.
Якщо
![]() визначена в точці
визначена в точці
![]() і
і
![]() ,
то кажуть, що
,
то кажуть, що
![]() неперервна в точці
неперервна в точці
![]() зліва.
зліва.
Якщо
функція
![]() неперервна в кожній точці інтервалу
неперервна в кожній точці інтервалу
![]() ,
то її називають неперервною в інтервалі
,
то її називають неперервною в інтервалі
![]() .
.
Функція
![]() називається неперервною на відрізку
називається неперервною на відрізку
![]() ,
якщо вона неперервна на інтервалі
,
якщо вона неперервна на інтервалі
![]() і на його кінцях відповідно зліва та
справа.
і на його кінцях відповідно зліва та
справа.
