
Решение нелинейных уравнений
.docРешение нелинейных уравнений
Пусть требуется решить уравнение
![]() ,
(1)
,
(1)
Где
![]() – нелинейная непрерывная функция.
– нелинейная непрерывная функция.
Методы решения уравнений делятся на прямые и итерационные. Прямые методы – это методы, позволяющие вычислить решение по формуле (например, нахождение корней квадратного уравнения). Итерационные методы – это методы, в которых задается некоторое начальное приближение и строится сходящаяся последовательность приближений к точному решению, причем каждое последующее приближение вычисляется с использованием предыдущих
![]()
Полное решение поставленной задачи можно разделить на 3 этапа:
-
Установить количество, характер и расположение корней уравнения (1).
-
Найти приближенные значения корней, т.е. указать промежутки, в которых наудится корни (отделить корни).
-
Найти значение корней с требуемой точностью (уточнить корни).
Существуют различные графические и аналитические методы решения первых двух задач.
Наиболее
наглядный метод отделения корней
уравнения (1) состоит в определении
координат точек пересечения графика
функции![]() с осью абсцисс. Абсциссы
с осью абсцисс. Абсциссы
![]() точек
пересечения графика
точек
пересечения графика![]() с осью
с осью
![]() являются
корнями уравнения (1)
являются
корнями уравнения (1)
Промежутки изоляции корней уравнения (1) можно получить аналитически, опираясь на теоремы о свойствах функций, непрерывных на отрезке.
Если,
например, функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() и
и
![]() ,
то согласно теореме Больцано – Коши,
на отрезке
,
то согласно теореме Больцано – Коши,
на отрезке
![]() существует
хотя бы один корень уравнения (1)(нечетное
количество корней).
существует
хотя бы один корень уравнения (1)(нечетное
количество корней).
Если
функция
![]() удовлетворяет
условиям теоремы Больцано—Коши и
монотонна на этом отрезке, то на
удовлетворяет
условиям теоремы Больцано—Коши и
монотонна на этом отрезке, то на
![]() существует
только один корень уравнения (1).Таким
образом, уравнение (1) имеет на
существует
только один корень уравнения (1).Таким
образом, уравнение (1) имеет на
![]() единственный
корень, если выполняются условия:
единственный
корень, если выполняются условия:
-
Функция
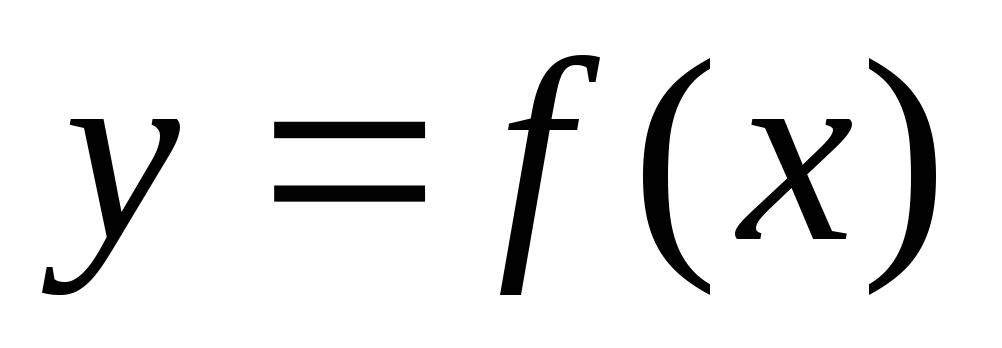 –
непрерывна на
–
непрерывна на
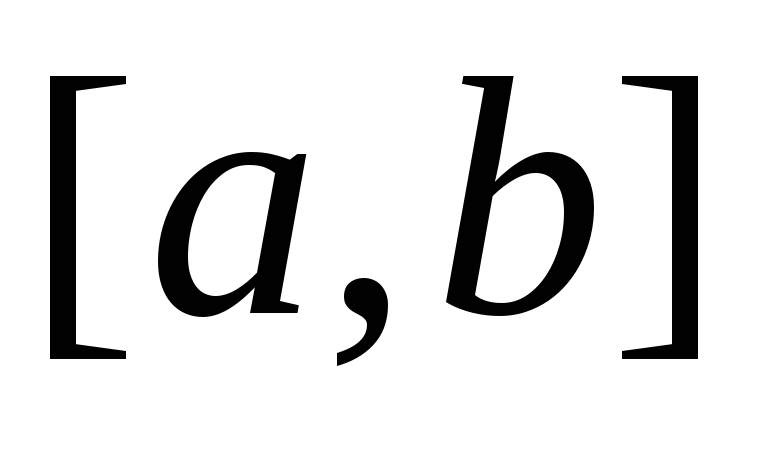 .
. -
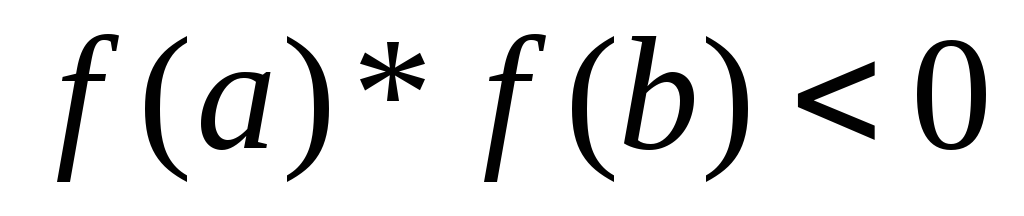 (2)
(2) -
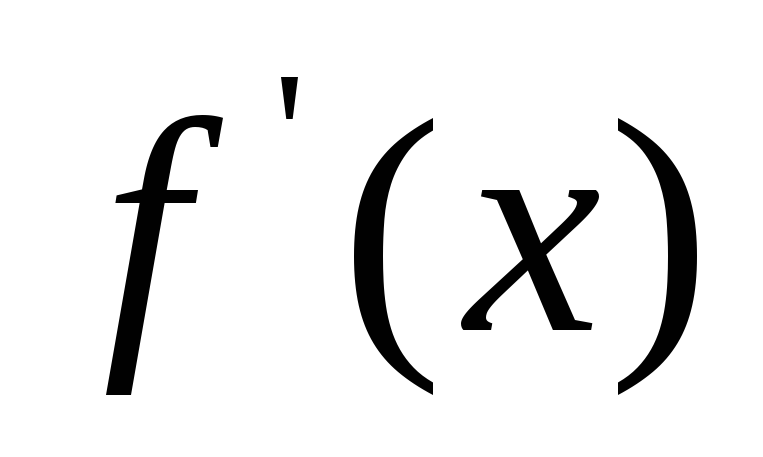 сохраняет
знак на
сохраняет
знак на
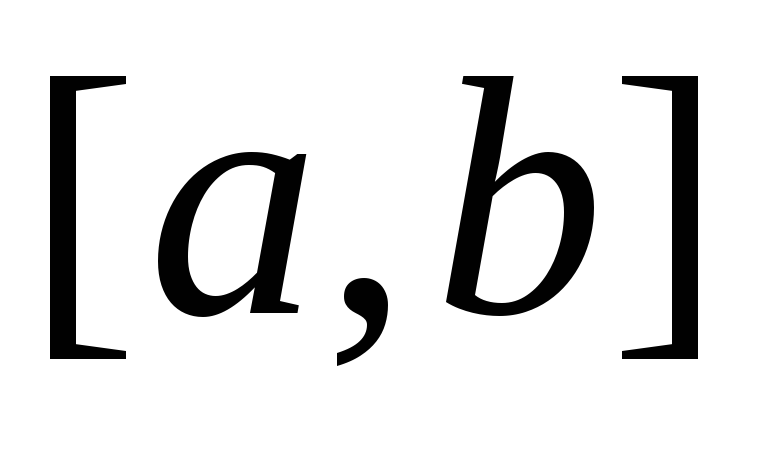 (монотонна на
(монотонна на
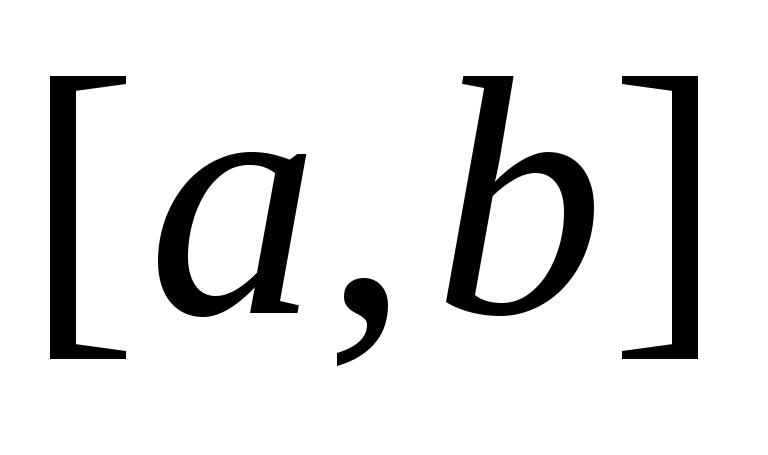 ).
).
Если функция на заданном интервале непрерывно дифференцируема, то можно воспользоваться следствием из теоремы Ролля, по которому между парой корней всегда находится по крайней мере одна стационарная точка. Алгоритм решения задачи в данном случае будет следующий:
-
Находим производную
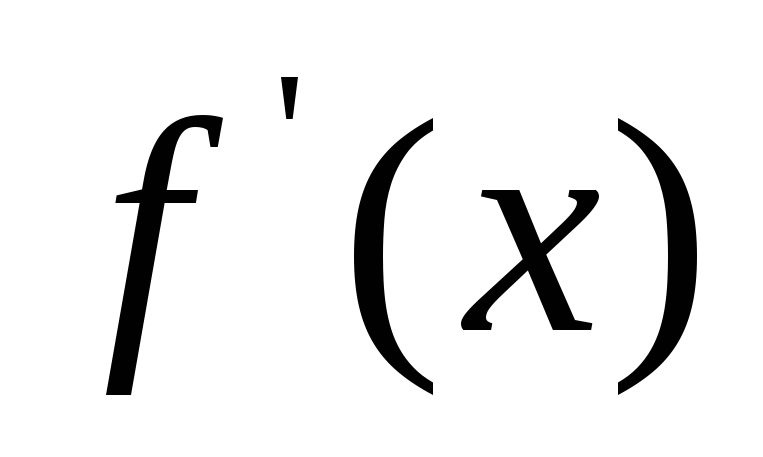 .
. -
Решаем уравнение
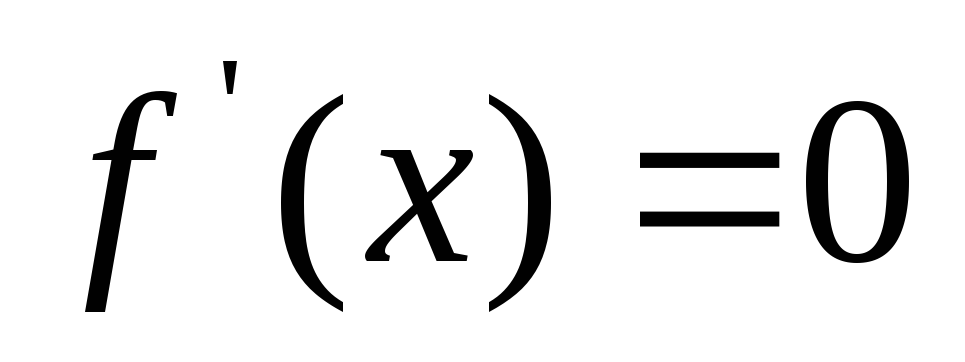 для
нахождения стационарных точек.
для
нахождения стационарных точек. -
Разбиваем исходный интервал
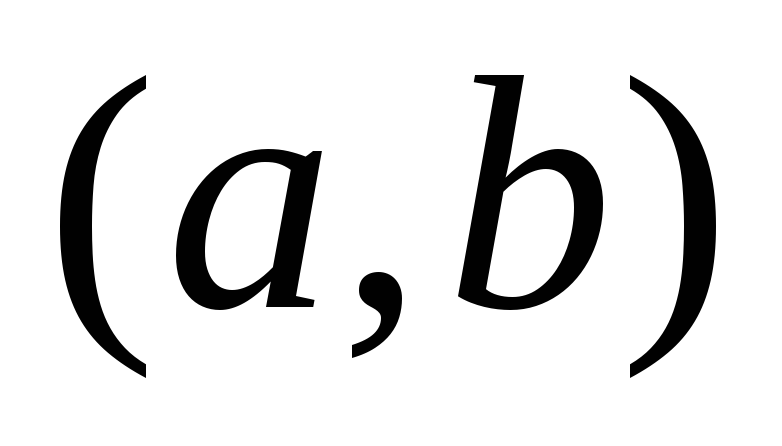 на
меньшие интервалы с помощью найденных
стационарных точек.
на
меньшие интервалы с помощью найденных
стационарных точек. -
Из полученных интервалов выбираем только те, на концах которых принимает значение разных знаков.
-
Уточняем интервалы за счет их сужения.
Полезным средством для отделения корней является также использование теоремы Штурма.
Решение третьей задачи осуществляется различными итерационными (численными) методами: методом дихотомии, методом простой итерации, методом Ньютона, методом хорд и т.д.
Пример
Решим
уравнение
![]() методом
простой
итерации.
Зададим
методом
простой
итерации.
Зададим
![]() .
Построим
график функции.
.
Построим
график функции.
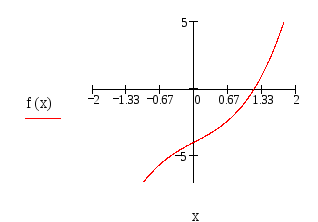
На
графике видно, что корень нашего уравнения
принадлежит отрезку
![]() ,
т.е.
,
т.е.
![]() – отрезок изоляции корня нашего
уравнения. Проверим это аналитически,
т.е. выполнение условий (2):
– отрезок изоляции корня нашего
уравнения. Проверим это аналитически,
т.е. выполнение условий (2):
-
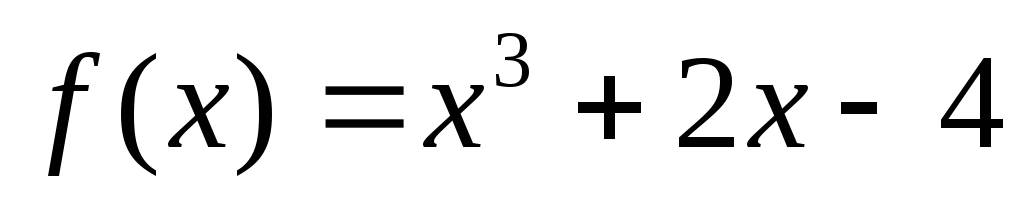 непрерывна
на
непрерывна
на
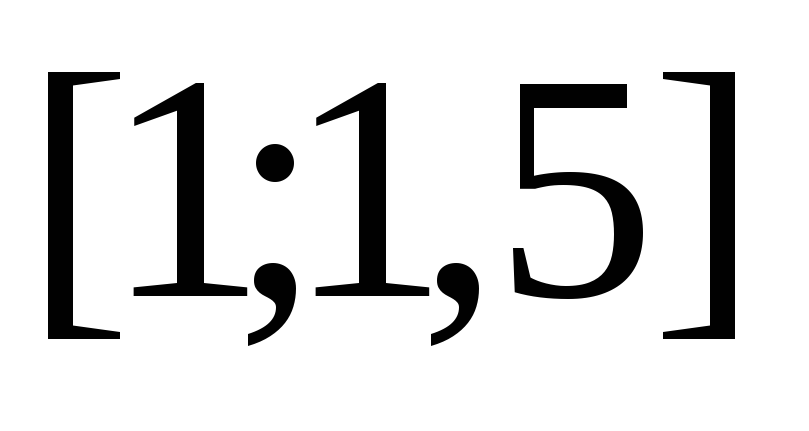 .
. -
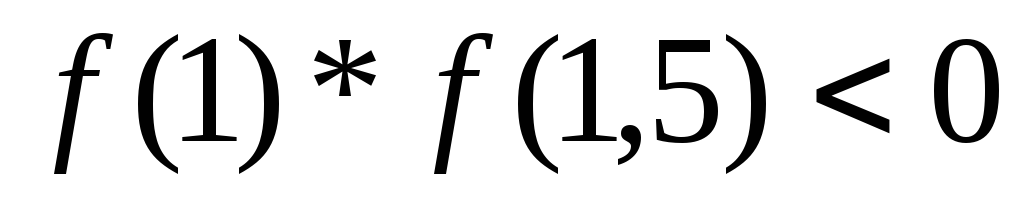 .
. -
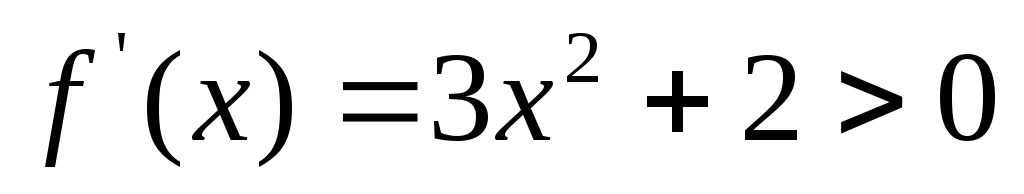 на
на
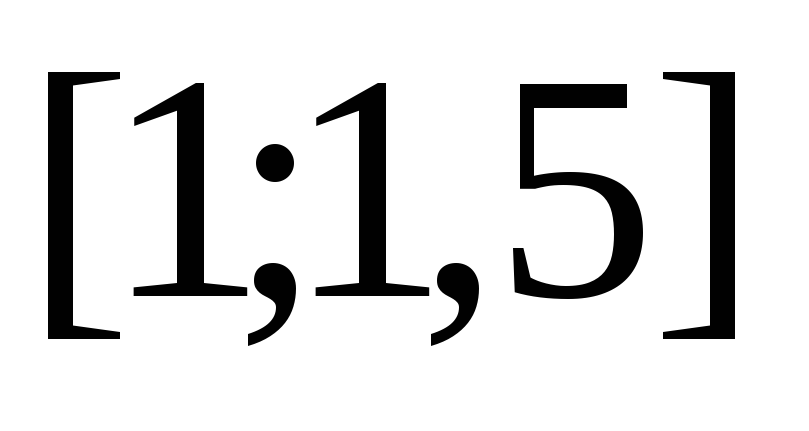 .
.
Напомним,
что исходное уравнение (1) в методе
простой итерации преобразуется к виду
![]() и итерации осуществляются по формуле:
и итерации осуществляются по формуле:
![]()
![]() (3)
(3)
Выполнение
расчетов по формуле (3) называется одной
итерацией. Итерации прекращаются, когда
выполняется условие
![]() ,
где
,
где
![]() -
абсолютная погрешность нахождения
корня, или
-
абсолютная погрешность нахождения
корня, или
![]() ,
где
,
где
![]() -относительная
погрешность.
-относительная
погрешность.
Метод
простой итерации сходится, если
выполняется условие
![]() для
для![]() .
Выбором функции
.
Выбором функции
![]() в формуле (3) для итераций можно влиять
на сходимость метода. В простейшем
случае
в формуле (3) для итераций можно влиять
на сходимость метода. В простейшем
случае
![]() со знаком плюс или минус.
со знаком плюс или минус.
На
практике часто выражают
![]() непосредственно из уравнения (1). Если
не выполняется условие сходимости,
преобразуют его к виду (3) и подбирают .
Представим наше уравнение в виде
непосредственно из уравнения (1). Если
не выполняется условие сходимости,
преобразуют его к виду (3) и подбирают .
Представим наше уравнение в виде
![]() (выразим
x
из уравнения). Проверим условие сходимости
метода:
(выразим
x
из уравнения). Проверим условие сходимости
метода:
![]() для
для
![]() .
Обратите внимание, что условие
сходимости выполняется не
.
Обратите внимание, что условие
сходимости выполняется не
![]() ,
поэтому мы и берем отрезок изоляции
корня
,
поэтому мы и берем отрезок изоляции
корня
![]() .
Попутно заметим, что при представлении
нашего уравнения в виде
.
Попутно заметим, что при представлении
нашего уравнения в виде
![]() ,
не выполняется условие сходимости
метода:
,
не выполняется условие сходимости
метода:
![]() на
отрезке
на
отрезке
![]() .
На графике видно, что
.
На графике видно, что
![]() возрастает быстрее, чем функция
возрастает быстрее, чем функция
![]()
(|tg|
угла наклона касательной к
(|tg|
угла наклона касательной к
![]() на отрезке
на отрезке
![]() )
)
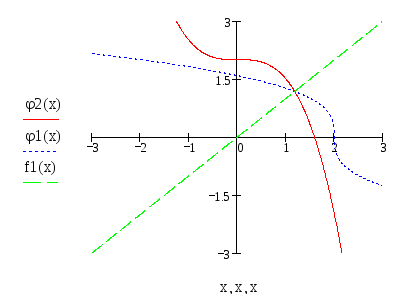
Выберем
![]() .
Организуем итерации по формуле:
.
Организуем итерации по формуле:
![]()
![]()
![]()
![]()
Программно организуем процесс итераций с заданной точностью:
> fv:=proc(f1,x0,eps)
> k:=0:
x1:=x0:
x:=x1+1:
while abs(x1-x)> eps do
x:=x1 :
x1:=f1(x):
print(evalf(x1,8)):
print(abs(x1-x)):
k:=k+1
od
:printf("Кол. итер.=%d ",k):
end:
На
19 итерации мы получили корень нашего
уравнения
![]()
![]() c
абсолютной погрешностью
c
абсолютной погрешностью
![]()
![]()
Решим наше уравнение методом Ньютона. Итерации в методе Ньютона осуществляются по формуле:
![]()
Метод Ньютона можно рассматривать как метод простой итерации с функцией , тогда условие сходимости метода Ньютона запишется в виде:
![]() .
.
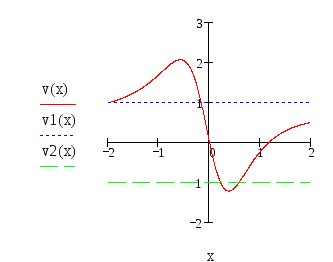
В
нашем обозначении
![]() и условие сходимости выполняется на
отрезке
и условие сходимости выполняется на
отрезке
![]() ,
что видно на графике:
,
что видно на графике:
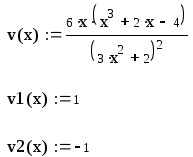
Напомним,
что метод Ньютона сходится с квадратичной
скоростью и начальное приближение
должно быть выбрано достаточно близко
к корню.
Произведем
вычисления:
![]() ,
начальное приближение ,
.
Организуем
итерации по формуле:
,
начальное приближение ,
.
Организуем
итерации по формуле:
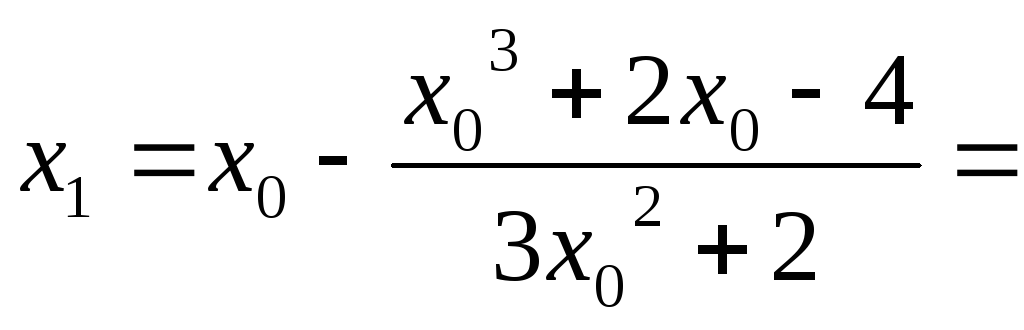
![]()

![]()
Программно
организуем процесс итераций с заданной
точностью![]() .
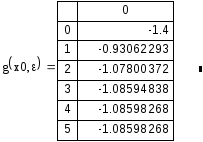
На
4 итерации получим корень уравнения
.
На
4 итерации получим корень уравнения
![]()
![]() с
с
![]() Мы
рассмотрели методы решения нелинейных
уравнений на примере кубических
уравнений, естественно, этими методами
решаются различные виды нелинейных
уравнений. Например, решая уравнение
Мы
рассмотрели методы решения нелинейных
уравнений на примере кубических
уравнений, естественно, этими методами
решаются различные виды нелинейных
уравнений. Например, решая уравнение
![]()
методом
Ньютона с
![]() ,
находим корень уравнения на [-1,5;-1]:
,
находим корень уравнения на [-1,5;-1]:
Задание:
Решить нелинейные уравнения с точностью
![]()
0.
![]()
-
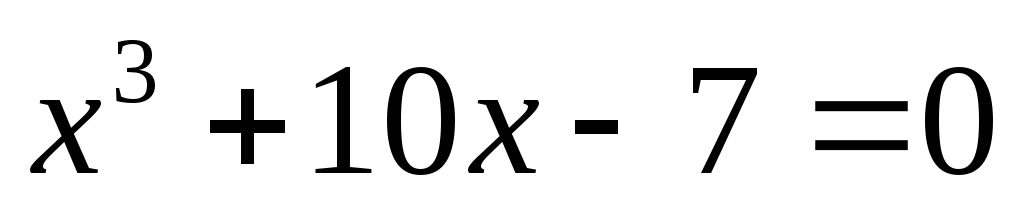
-
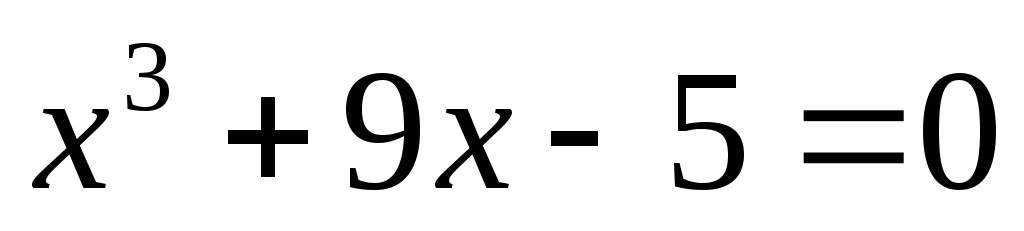
-
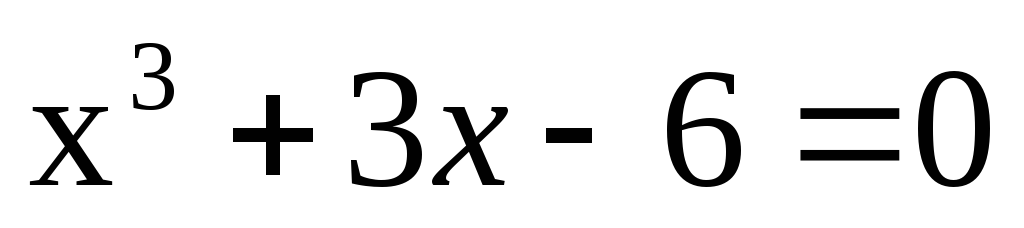
-
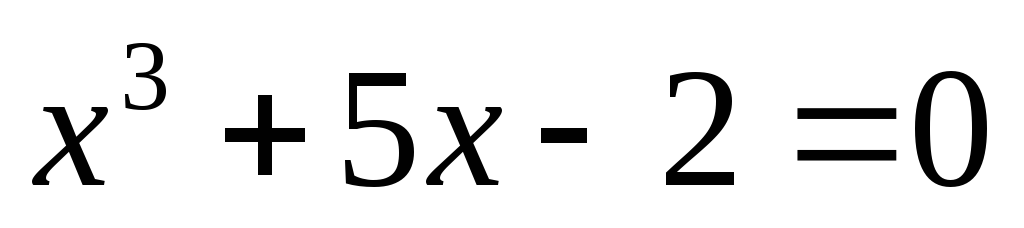 методами:
методами:
-
деления отрезка пополам (дихотомии)
-
простой итерации.
-
хорд.
-
Ньютона (касательных)
-
секущих – хорд.
Варианты
заданий рассчитываются следующим
образом: номер по списку делится на 5
(![]() ),
целая часть соответствует номеру
уравнения, остаток – номеру метода.
),
целая часть соответствует номеру
уравнения, остаток – номеру метода.
