Применения сети Хопфилда к задачам комбинаторной оптимизации.

Ассоциативность памяти нейронной сети Хопфилда не является единственным ее достоинством, которое используется на практике. Другим важным свойством этой архитектуры является уменьшение ее функции Ляпунова в процессе нейродинамики. Следовательно, нейросеть Хопфилда можно рассматривать, как алгоритм оптимизации целевой функции в форме энергии сети.

Класс целевых функций, которые могут быть минимизированы нейронной сетью достаточно широк: в него попадают все билинейные и квадратичные формы с симметричными матрицами. С другой стороны, весьма широкий круг математических задач может быть сформулирован на языке задач оптимизации. Сюда относятся такие традиционные задачи, как дифференциальные уравнения в вариационной постановке; задачи линейной алгебры и системы нелинейных алгебраических уравнений, где решение ищется в форме минимизации невязки, и другие.

Исследования возможности использования нейронных сетей для решения таких задач сегодня сформировали новую научную дисциплину - нейроматематику.

Применение нейронных сетей для решения традиционных математических задач выглядит весьма привлекательным, так нейропроцессоры являются системами с предельно высоким уровнем параллельности при обработке информации. В нашей книге мы рассмотрим использование нейро-оптимизаторов для несколько иных задач, а именно, задач комбинаторной оптимизации.

Многие задачи оптимального размещения и планирования ресурсов, выбора маршрутов, задачи САПР и иные, при внешней кажущейся простоте постановки имеют решения, которые можно получить только полным перебором вариантов. Часто число вариантов быстро возрастает с числом структурных элементов N в задаче (например, как N! - факториал N), и поиск точного решения для практически полезных значений N становится заведомо неприемлимо дорогим. Такие задачи называют неполиномиально сложными или NP-полными. Если удается сформулировать такую задачу в терминах оптимизации функции Ляпунова, то нейронная сеть дает весьма мощный инструмент поиска приближенного решения.

Рассмотрим классический пример NP-полной проблемы - так называемую задачу комивояжера (бродячего торговца). На плоскости расположены N городов, определяемые парами их географических координат: (x_i,y_i), i=1..N. Некто должен, начиная с произвольного города, посетить все эти города, при этом в каждом побывать ровно один раз. Проблема заключается в выборе маршрута путешествия с минимально возможной общей длиной пути.

Полное число возможных маршрутов равно , и задача поиска кратчайшего из них методом перебора весьма трудоемка. Приемлимое приближенное решение может быть найдено с помощью нейронной сети, для чего, как уже указывалось, требуется переформулировать задачу на языке оптимизации функции Ляпунова (J.J.Hopfield, D.W.Tank, 1985).

Обозначим названия городов заглавными буквами (A, B, C, D...). Произвольный маршрут может быть представлен в виде таблицы, в которой единица в строке, отвечающей данному городу, определяет его номер в маршруте.

Таб. 9.1. Маршрут B-A-C-D ...

	Номер
Город	1	2	3	4	...
A	0	1	0	0	...
B	1	0	0	0	...
C	0	0	1	0	...
D	0	0	0	1	...
...	...	...	...	...	...

Сопоставим теперь клетке таблицы на пересечении строки X и столбца i нейрон S_xi из {0,1}. Возбужденное состояние данного нейрона сигнализирует о том, что город X в маршруте следует посещать в i-тую очередь. Составим теперь целевую функцию E(S) задачи поиска оптимального маршрута. Она будет включать 4 слагаемых:

Первые три слагаемых отвечают за допустимость маршрута: каждый город должен быть посещен не более чем один раз (в каждой строке матрицы имеется не более одной единицы), под каждым номером должно посещаться не более одного города (в каждом столбце - не более одной единицы) и, кроме того, общее число посещений равно числу городов N (в матрице всего имеется ровно N единиц):

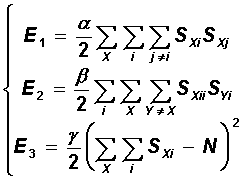
Видно, что каждое из этих трех слагаемых обращается в нуль на допустимых маршрутах, и принимает значения больше нуля на недопустимых. Последнее, четвертое слагаемое минимизирует длину маршрута:

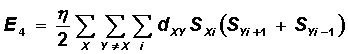
Здесь за d_XY обозначено расстояние между городами X и Y. Заметим, что отрезок пути X-Y включается в сумму только тогда, когда город Y является относительно города X либо предыдущим, либо последующим. Множители  ,  ,  и  имеют смысл относительных весов слагаемых.

Общий вид функции Ляпунова сети Хопфилда дается выражением:

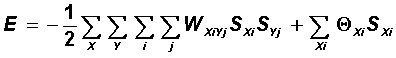
Полученная целевая функция из четырех слагаемых представляется в форме функции Ляпунова, если выбрать значения весов и порогов сети в следующем виде:

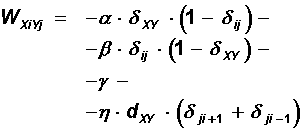
Теперь можно заменить обучение Хебба прямым заданием указанных весов и порогов для нейросети, и динамика полученной системы будет приводить к уменьшению длины маршрута комивояжера. В этой задаче целесообразно использовать вероятностную динамику с имитацией отжига, так как наибольший интерес представляет глобальный минимум энергии.

Хопфилдом и Тэнком изложенная модель была опробована в вычислительном эксперименте. Нейронной сети удавалось находить близкие к оптимальным решения за приемлемые времена даже для задач с несколькими десятками городов. В дальнейшем последовало множество публикаций о разнообразных применениях нейросетевых оптимизаторов. В завершении лекции рассмотрим одно из таких применений - задачу о расшифровке символьного кода.

Пусть имеется некоторое (достаточно длинное) текстовое сообщение, написанное на некотором языке с использованием алфавита A, B, C ... z и символа “пробел”, отвечающего за промежуток между словами. Данное сообщение закодировано таким образом, что каждому символу, включая пробел, сопоставлен некоторый символ из ряда i,j,k, .... Требуется расшифровать сообщение.

Данная задача также относится к числу NP-полных, общее число ключей шифра имеет факториальную зависимость от числа символов в алфавите. Приближенное нейросетевое решение может быть основано на том факте, что частоты появления отдельных символов и конкретных пар символов в каждом языке имеют вполне определенные значения (например, в русском языке частота появления буквы “а” заметно превосходит частоту появления буквы “у”, слог “во” появляется довольно часто, а, например, сочетание “йщ” вовсе не возможно).

Частоты появления символов P_i и их пар P_ij в закодированном сообщении можно вычислить непосредственно. Имея, далее, в распоряжении значения P_A частот появления символов языка и их пар P_AB , следует отождествить их с вычисленными значениями для кода. Наилучшее совпадение и даст требуемый ключ.

Целевая функция этой задачи содержит пять слагаемых. Первые три слагаемых полностью совпадают с тремя первыми членами в выражении для энергии в задаче о комивояжере. Они определяют допустимость ключа (каждому символу языка соответствует один символ кода). Остальные слагаемые отвечают за совпадение частот отдельных символов и частот пар в коде и языке.

Полное выражение для целевой функции имеет вид:

Целевая функция также как и для задачи комивояжера, приводится к виду функции Ляпунова, после чего нейронная сеть выполняет требуемую расшифровку.

Алгоритм обучения слоя персептронов разделению нескольких классов

Существует три случая линейной разделимости m классов

Случай 1. Для каждого класса ϖi существует линейная решающая функция di(x) =(wi ,x), отделяющая этот класс от всех остальных классов. В этом случае задача нахождения ЛРФ di сводится к разделению двух классов: ϖ′ и ϖ′′ ={ϖ1,...,ϖi−1,ϖi+1,...,ϖm}.

Случай 2. Любой класс ϖi отделяется от любого другого класса ϖ j с помощью одной ЛРФ вида dij (x) =(wij ,x). Использование алгоритма персептрона сводится к разделению двух классов. Из обучающей выборки нужно выбрать только те элементы, которые принадлежат классам ϖi и ϖ j .

Случай 3. Для разделения m классов используется m−1 линейная решающая функция di(x) =(wi ,x), причем x∈ϖ ,если di(x)>0 и dj (x)≤0 для всех j ≠i .

Алгоритм нахождения системы линейных решающих функций в третьем случае может быть реализован на слое из m персептронов. Такие модели называют обобщенными персептронами. На входы всех персептронов подается вектор x. Если вектор x∈ϖi , то выходное значение i -го персептрона должно быть положительным, а для всех остальных персептронов – отрицательным.

Для обучения такого слоя из m персептронов будем использовать следующий алгоритм.

Алгоритм обучения слоя персептронов

1. Инициируются начальные значения w1(0) ,…,wm(0) весовых векторов всех персептронов.

2. Обобщенному персептрону предъявляется очередной вектор xk ∈Ξ∞ из обучающей выборки и осуществляется коррекция весовых векторов по правилу:

ω_i^(k), если(ω_i^(k),x_k)>0 и x_k∈ϖ_i, (ω_i^(k),x_k)≤0 и x_k∉ϖ_i, 

ω_i^(k+1)= ωi(k) +xk , если(ωi(k),xk )≤0иxk∈ϖi , 

ω_i^(k)−x_k, если(ω_i^(k),x_k)>0 и x_k∉ϖ_i.

3. Проверяется условие останова для найденных весовых векторов: алгоритм завершает свою работу, если он N раз подряд правильно классифицирует элементы обучающей выборки. В противном случае – переход к пункту 2.

После появления персептронов (в том числе и обобщенных) наблюдался значительный интерес к исследованиям в этой области. Изучалась сходимость алгоритма обучения персептрона (А. Новиков), исследовались возможности таких систем, рассматривались различные обобщения модели персептрона, открывались новые области их применения. Однако долгое время не было строгого математического обоснования их работы. Поэтому первые неудачи, когда не удавалось обучить персептрон решению некоторых простых задач, не воспринимались фатально. Ситуация кардинально изменилась после появления книги Марвина Минского (Minskiy M.) и Сеймера Пейперта (Papert S.) «Персептроны» в 1969 году, в которой авторы, с одной стороны, математически описали работу персептронов, с другой стороны, указали границы их применения. Эти ограничения в основном связаны с линейным характером тех задач, которые могут решаться персептронами и экспоненциальным ростом сложности персептронов при возрастании размерности решаемых задач. В нейроинформатике начался затяжной, более чем десятилетний, кризис, который закончился только в 1982 году, когда появились первые работы по обучению многослойных нейронных сетей, способных решать задачи нелинейного характера.

Математические возможности нейронных сетей

НС могут вычислять линейные функции, нелинейные функции одного переменного, а также всевозможные суперпозиции – функции от функций, получаемые при каскадном соединении сетей. Совокупность этих операций позволяет вычислять широкий класс функций, множество которых описывается следующими теоремами. Первая теорема была доказана (в разных вариантах) в 1954-1956 годах А.Н. Колмогоровым и его учеником, тогда студентом В.И. Арнольдом. Эта теорема, по сути, является решением 13-й проблемы Гильберта: можно ли непрерывную функцию многих переменных получить с помощью арифметических операций и суперпозиции из непрерывных функций двух переменных?

Теорема 6.2. Каждая непрерывная функция f (x) , x∈[0,1]n представима в виде

2n+1  n 

f (x)=∑gj ∑hkj(xk),

j=1  k=1 

где gj (t) – непрерывные функции, hkj(xk ) – непрерывные функции, не зависящие от функции f .

Теорема 6.2 говорит о точном представлении непрерывной функции с помощью суперпозиции функций одной переменной. Вычисление функции f можно было бы реализовать с помощью НС, но так как функции gj зависят от функции f , то с помощью такой сети можно реализовать вычисление только одной заданной функции.

На практике, однако, как правило, нет необходимости добиваться точного представления при вычислении функций. Достаточно уметь вычислять функции приближенно с заданной степенью точности. Поэтому важным является вопрос об аппроксимации функций. Фундаментальной здесь является следующая теорема Вейерштрасса.

Теорема 6.3. Любая непрерывная функция f (x) на любом компактном множестве K⊆Rn может быть равномерно приближена многочленами, т.е. для любого ε >0 существует многочлен P(x) такой, что sup f (x)−P(x) <ε . x∈K

Эта теорема имеет ряд сильных обобщений, связанных с идеологией нейронных сетей. Одним из таких обобщений является следующая теорема, доказанная Стоуном1 в 1948 году. Пусть K компактное множество и C(K) – множество непрерывных на K вещественных функций. Тогда C(K) – алгебра (т.е. линейное пространство, замкнутое относительно операции произведения функций и удовлетворяющее аксиомам ассоциативности по умножению и дистрибутивности).

Теорема 6.4. Если замкнутая (по равномерной норме) подалгебра E⊆C(K) содержит единицу и разделяет точки из K (т.е. для любых двух различных точек x, y∈K существует такая функция p∈E , что p(x)≠ p(y)), то E=C(K).

Если в качестве E взять множество всех многочленов, то получим утверждение классической теоремы Вейерштрасса. Однако в качестве E можно взять и множество тригонометрических многочленов, и множество экспонент и т.д. И вообще достаточно взять любой набор функций, разделяющий точки, построить из них кольцо многочленов и мы получим плотное в C(K) множество функций.

Формальный стандартный нейрон может вычислять линейную функцию многих переменных и нелинейную функцию одного переменного. Поэтому с точки зрения конструирования нейронных сетей представляет интерес вопрос об аппроксимации функций многих переменных суперпозициями функций одной переменной и линейных комбинаций многих переменных. Этот вопрос был положительно решен А.Н. Горбанем2 в 1998 году.

Теорема 6.5. Пусть C(K) – линейное пространство, а E – замкнутое линейное подпространство в C(K) , содержащее единицу, разделяющее точки из K и замкнутое относительно нелинейной унарной операции h∈C(R). Тогда E=C(K).

Из теоремы 6.5 следует теорема 6.4, если в качестве унарной операции взять h(t)=t2 . Тогда из равенства fg = 12 (( f +g)2 − f 2 −g2) следует, что замкнутость E относительно функции h(t)=t2 равносильна замкнутости относительно произведения функций и, следовательно, равносильна тому, что E будет кольцом (подалгеброй).

Теорема 6.5 утверждает, что с помощью нейронной сети, в которой используется любая нелинейная функция активации, можно организовать вычисление значений любой непрерывной функции с любой степенью точности. Однако эта теорема не говорит о сложности такой сети – количестве слоев, числе нейронов в слоях.