Проекции нечетких отношений

Важную роль в теории нечетких множеств играет понятие проекции нечеткого отношения. Дадим определение проекции бинарного нечеткого отношения.

Пусть — функция принадлежностинечеткого отношения в .Проекции иотношениянаи— есть множества вис функцией принадлежности вида

Условной проекцией нечеткого отношения на, при произвольном фиксированном, называется множествос функцией принадлежности вида.

Аналогично определяется условная проекция на при заданном:

Из данного определения видно, что проекции ине влияют на условные проекциии, соответственно. Дадим далее определение, которое учитывает их взаимосвязь.

Условные проекции второго типа определяются следующим образом:

Если или, то полагаем, соответственно, чтоили.

Заметим, что условные проекции первого типа содержатся в соответствующих проекциях второго типа.

Пусть и— базовые множества,—нечеткое отношение в ии— его проекции наи, соответственно.

Нечеткие множества иназываютсянезависимыми, если

Следовательно, они независимы по первому типу, если

и независимы по второму типу, если

В противном случае проекции иявляются зависимыми (соответствующего типа).

Независимость второго типа можно интерпретировать следующим образом. Данные соотношения с учетом произвольности иперепишем в виде

Классы нечетких отношений

Все типы нечетких отношений в зависимости от свойств, которыми они обладают, могут быть разделены на три больших класса. В первый класс входят симметричные отношения, которые обычно характеризуют сходство или различие между объектами множества . Второй класс образуют антисимметричные отношения; они задают на множествеотношения упорядоченности, доминирования, подчиненности и т.п. Третий класс состоит из всех остальных отношений.

Отношения каждого класса, в свою очередь, могут быть разделены на подклассы в зависимости от выполнения условий рефлексивности и антирефлексивности.

Рефлексивные и симметричные отношения обычно называют отношениями сходства, толерантности, безразличия или неразличимости. В дальнейшем эти отношения будем называть отношениями сходства и обозначать буквой . Антирефлексивные и симметричные отношения называются отношениями различия и обозначаются буквой. Отношения сходства и отношения различия двойственны друг другу.Антисимметричные отношения, называемые предпорядками и обозначаемые буквой , в зависимости от выполнения условия рефлексивности или антирефлексивности делятся на нестрогие и строгие порядки.

Из отношений третьего класса, обозначаемых буквой , обычно выделяют лишь рефлексивные отношения, которые будут называться слабыми порядками.

На следующем уровне классификации из каждого класса отношений могут быть выделены отношения специального вида. Определяющим условием для них является условие транзитивности. Оно устанавливает связь между силой отношения для различных пар объектов из . Эта связь может быть очень слабой, а может накладывать достаточно сильные ограничения на возможные значения силы отношения между объектами из. Число отличающихся друг от друга условий транзитивности зависит от типа отношения, для которого они формулируются.

Условия транзитивности зависят от вида операций, с помощью которых они определяются. Наиболее общими условиями транзитивности являются условия, определяемые с помощью решеточных операций ив. Более частыми являются условия, определяемые с помощью дополнительных операций ви зависящих от конкретного вида. В этих случаях указывается вид соответствующего множества. Далее мы будем рассматривать нечеткие отношения, определенные на множестве.

Отношения сходства и различия

Симметричное и рефлексивное нечеткое отношение сходства является аналогом обычного отношения толерантности. Нечеткие отношения сходства обычно задаются с помощью матриц сходства, связи между объектами, либо с помощью неориентированных взвешенных графов. Матрицы сходства могут быть получены как в результате измерения некоторого физического параметра, так и в результате опроса экспертов, которые для каждой пары объектов из указывают их степень сходства в некоторой шкале сравнений.

Условие транзитивности для нечетких отношений сходства обычно формулируются в виде

которое при различных определениях операции композиции приводит к различным условиям транзитивности. Наиболее распространенными условиями транзитивности являются следующие:

• ( )-транзитивность

• ( )-транзитивность

• ( )-транзитивность

Наиболее интересными свойствами обладает ( )-транзитивное отношение сходства, которое является обобщением обычного отношения эквивалентности. Это отношение называетсянечетким отношением эквивалентности или отношением подобия. Нетрудно показать, что любой -уровень нечеткого отношения эквивалентности является обычным отношением эквивалентности и, следовательно, определяет разбиение множества объектовна непересекающиеся классы эквивалентности. Из вложенности-уровней нечеткого отношения следует и вложенность разбиений множества, соответствующих различным-уровням, причем с уменьшениемпроисходит укрупнение классов эквивалентности-уровней. Таким образом, нечеткое отношение эквивалентности задает иерархическую совокупность разбиений множествана непересекающиеся классы эквивалентности.

Нечеткое отношение эквивалентности, в отличие от произвольного отношения сходства, определяет совокупность разбиений множества на классы эквивалентности, благодаря тому, что условие транзитивности накладывает дополнительно сильные ограничения на возможные значения степени принадлежности. В случае, когда, отношение сходстватранзитивно тогда и только тогда, если для любыхиз трех чисел, по крайней мере, два числа равны друг другу и по величине не превышают третье. Таким образом, нечеткое отношение эквивалентности обладает многими полезными свойствами из-за своего довольно специфического вида.

отношением различия называется симметричное и антирефлексивное нечеткое отношение. Отношение различия двойственно отношению сходства. В случае, когда , эти отношения могут быть получены друг из друга с помощью соотношения:

что можно записать в алгебраической форме как .

Ультраметрикой называется отношение различия, удовлетворяющее следующему неравенству:

Очевидно, что это условие двойственно условию ( )-транзитивности. Понятие ультраметрики первоначально возникло и изучалось в кластерном анализе при исследовании свойств меры различия между объектами, определяющих естественное представление множества объектов в виде дерева разбиений. Представление ультраметрики с помощью системы вложенных друг в друга отношений эквивалентности было также известно в кластерном анализе, однако лишь в рамках теории нечетких отношений это представление получило естественное объяснение.

Метрикой называется отношение различия, удовлетворяющее неравенству треугольника:

От метрики обычно требуют выполнения условия сильной антирефлексивности. Метрика, удовлетворяющая лишь простому условию антирефлексивности, называется псевдометрикой. Двойственным по отношению к метрике является ( )-транзитивное отношение сходства.

Двойственным условию ( )-транзитивности является следующее условие:

Задачи нечеткой классификации

Пусть имеется набор фотографических портретов всех членов нескольких семей. Требуется разделить этот набор на группы так, чтобы в каждой оказались портреты членов только одной семьи. Пусть— функция принадлежности нечеткого бинарного отношения сходства на заданном наборе фотографий. Для каждой пары фотографийизначениеесть субъективная оценка человеком степени сходстваи. Это нечеткое отношение можно рассматривать как своего рода "экспериментальные данные", отражающие понимание человеком понятия "сходства" в данной задаче. Следующий этап — использование этих "данных" для требующейся классификации фотографий.

Заметим, что нечеткое отношение обладает естественными свойствами рефлексивности и симметричности. Оно называется одношаговым отношением, в том смысле, что описывает результаты лишь попарного сравнения портретов друг с другом. Длявводится-шаговое отношениеследующим образом:

Это отношение является -арной композицией исходного "экспериментального" отношенияи представляет собой в некотором смысле его уточнение. Нетрудно показать, что для любыхвыполняется цепочка неравенств

из которой следует, в частности, что для любых последовательностьимеет предел при. Таким образом, существует предельное отношение сходства, определяемое равенством

Это предельное отношение является конечным результатом обработки результатов нечетких измерений и следующим образом используется для классификации.

Для произвольного числа () вводится обычное (не нечеткое) отношение:

Нетрудно показать, что для любого ()есть отношение эквивалентности в, т.е. для любыхвыполняются обычные аксиомы эквивалентности

(1) —рефлексивность,

(2) —симметричность,

(3) —транзитивность.

Заметим, что (3) есть следствие того, что предельное нечеткое отношение обладает свойством нечеткой транзитивности

Окончательный этап алгоритма классификации — разбиение множества на классы эквивалентности по полученному отношению.

Выбор величины порога в этом алгоритме осуществляется, исходя из условий начальной задачи. В приведенном выше примере с фотографиями этот выбор осуществляли следующим образом. Пусть имеется набор из 20 фотографий представителей 3 семей. Тогда величинувыбирают так, чтобы в результате реализации алгоритма классификации получилось 3 класса эквивалентности по отношению.

Порядки и слабые порядки

Антисимметричное, транзитивное нечеткое отношение называется отношением упорядочения или порядком. Мы будем рассматривать только строгие порядки, т.е. порядки, для которых выполняется свойство антирефлексивности. Свойства нестрогих (рефлексивных)порядков во многом совпадают со свойствами строгих порядков.

Различные порядки отличаются друг от друга требованиями, предъявляемыми к условию транзитивности. Слабейшее из этих требований — условие ацикличности отношения строгого порядка , наиболее жесткие требования — условия линейной транзитивности и условие квазисерийности.

Если для отношения сходства условие транзитивности обычно записывают в виде и различные способы определения операции композиции позволяют задавать разные типы транзитивности, причем оказывается, что таких типов существует не так уж и много, то дляотношения порядка условие транзитивности нечеткого отношения удобно записывать в виде, аналогичном условию транзитивности обычных порядков:

где — некоторая операция в. Оказывается, что из множества всех отношений порядка можно выделить значительное количество отличающихся друг от друга классов порядков специального вида, определяемых как способом задания операциив, так и способом записи условия транзитивности. Далее перечислим некоторые условия транзитивности, определяющие эти классы нечетких строгих порядков. Учитывая асимметричность отношения строгого порядка, будем полагать, если.

• Ацикличность:

• Слабая транзитивность:

• Отрицательная транзитивность:

• ( )-транзитивность:

• ( )-транзитивность:

• ( )-транзитивность:

• Сильная транзитивность:

• Сверхсильная транзитивность:

• Метрическая транзитивность:

• Квазисерийность:

• Ультраметрическая транзитивность:

В общем случае предполагается, что рассмотренные условия транзитивности определены для , хотя некоторые условия могут быть обобщены и на случай, когдаявляется решеткой.

Условия ацикличности, слабой транзитивности и отрицательной транзитивности нечеткого отношения равносильны соответственно условиям ацикличности, транзитивности и отрицательной транзитивности обычного отношения, определяемого следующим образом:

Аналогичные свойства могут быть определены как -свойства для различных-уровнейотношения.

В отличие от первых трех свойств, остальные свойства более специфичны для нечетких отношений и в большей мере учитывают согласованность силы отношения между элементами множества . Для этих свойств также могут быть сформулированы-свойства.

Частным случаем сильного порядка (порядка, удовлетворяющего условию сильной транзитивности) является метрический порядок. Для асимметричных отношений условие метрической транзитивности эквивалентно неравенству треугольника.

Условие квазисерийности определяет нечеткую квазисерию. Каждый -уровень нечеткой квазисерии является обыкновенной квазисерией, т.е. удовлетворяет условиям

Поскольку обычная квазисерия определяет разбиение множества на упорядоченные классы эквивалентности, нечеткая квазисерия определяет разбиение множествана упорядоченные классы эквивалентности на каждом-уровне. Эти разбиения вложены друг в друга; таким образом, нечеткая квазисерия определяет иерархию разбиений множествана упорядоченные классы эквивалентности.

Частным случаем метрических порядков, помимо квазисерии, является линейный порядок, определяемый условием линейной транзитивности. Линейный порядок при интерпретации как силы предпочтения альтернативынад альтернативойзадает на множестве альтернативнекоторую аддитивную функцию полезности, которая может быть определена на, например, с помощью соотношения.

Ультраметрическая транзитивность построена по аналогии с метрической транзитивностью, однако для антисимметричных отношений она не эквивалентна ультраметрическому неравенству .

Между строгими порядками (асимметричными отношениями) и слабыми порядками (рефлексивными отношениями) существует тесная связь. Эти порядки могут быть получены друг из друга с помощью ряда преобразований.

Если на задана операция дополнения, т.е. такая унарная операция, что навыполняются тождества

то на множестве нечетких отношений может быть задана операция дополнения следующим образом:

и на множестве нечетких отношений будут выполняться тождества

Если на множестве нечетких отношений задана операция дополнения, то из отношения строгого порядка могут быть получены:

• Отношение сходства

• Отношение различия

• Отношение слабого порядка

Транзитивностью отношения определяется тот или иной уровень транзитивности отношенийи. В частности, еслиявляется нечеткой квазисерией, то определяемое им отношениеявляется нечетким отношением эквивалентности, а отношениебудет нечетким квазипорядком.

Нечеткие отношения порядка могут быть получены многими способами и допускают различную интерпретацию. Они могут выражать либо значение какого-либо физического параметра, характеризующего интенсивность доминирования над, либо усредненную по множеству критериев или индивидуумов силу предпочтения между объектами. Они могут быть получены с помощью шкалы сравнений, которой эксперты измеряют интенсивность предпочтений при попарных сравнениях альтернатив, могут выражать уверенность, возможность, вероятность доминирования и т.п.

Задачи нечеткого упорядочения

Любую задачу принятия решений можно сформулировать как задачу отыскания максимального элемента в множестве альтернатив с заданным в нем отношением предпочтения. Однако во многих реальных ситуациях в множестве альтернатив можно определить лишь нечеткое отношение предпочтения, т.е. указать для каждой пары альтернатив илишь степени, с которыми выполняются предпочтенияи. В таких случаях задача принятия решения становится неопределенной, поскольку неясно, что такое максимальный элемент для нечеткого отношения предпочтения. Для двух типов нечетких отношений можно предложить способы упорядочения элементов конечного множества, в котором задано нечеткое отношение. Способы эти сводятся к тому, что для каждого из рассматриваемых типов нечетких отношений строится некоторая функция (напоминающая функцию полезности), и элементы множества упорядочиваются по соответствующим им значениям этой функции.

Пусть — функция принадлежности бинарного нечеткого отношения в множестве(например, отношения нестрого предпочтения). Допустим, что рассматривается задача упорядочения элементов конечного множества. Упорядочение можно осуществлять по значениям следующей функции:

где , а функция

Для вычисления значений функции удобно пользоваться следующим равенством:

По отношению к этому упорядочению максимальным в множестве является элементтакой, что

Рассмотрим еще одну задачу упорядочения, иллюстрируемую следующим примером.

Требуется решить, кто из детей: старший сын , младший сынили дочьбольше всего похож на отца. Заданы "результаты измерений":ивзятые отдельно, похожи на отца со степенямиисоответственно;и, взятые отдельно, похожи на отца со степенямии; наконец,и, взятые отдельно, похожи на отца со степенямии.

Таким образом, в этой задаче, в отличие от предыдущей, имеется стандартный элемент (шаблон) для упорядочиваемого множества , т.е. элемент, обладающий свойствами, общими для всех элементов этого множества. Иначе говоря, если— нечеткое отношение в(например, отношение сходства), то

При наличии стандартного элемента для каждой пары элементов имножествазадаются величины,, т.е. степени отношения (например, сходства)и, взятых отдельно, к. Упорядочение элементов множествас заданным таким способом нечетким отношением предлагается осуществлять в соответствии со значениями функции

Максимальным в смысле этого упорядочения является элемент такой, что

Для задачи о сходстве отца и детей значения этой функции таковы:

Отсюда вытекает, что наиболее похож на отца старший сын, затем следуют дочь и младший сын.

Методы построения функции принадлежности. Классификация

С древних времен и до наших дней измерения как один из способов познания играют важную роль в жизни человека. Сначала человек в своей повседневной деятельности довольствовался информацией, доставляемой лишь его органами чувств, а затем привлек им в помощь средства измерительной техники.

Целью измерения является получение количественной информации о величине исследуемых объектов, под которыми понимаются реально существующие объекты (предметы, процессы, поля, явления и т.д.) материального мира, а также взаимодействия между ними. Задачи измерения могут быть как познавательными (изучение элементарных частиц, организма человека и т.д.), так и прикладными (управление конкретным технологическим процессом, контроль качества продукции). Получение и использование информации — характерное свойство кибернетических систем. Поэтому измерение можно рассматривать как ту часть кибернетики, которая принимает в качестве объекта исследования предметы и явления окружающего мира, в качестве метода — эксперимент, а в качестве средства — измерительную технику.

Существует тесная взаимосвязь между научно-техническим прогрессом и достижениями в области измерений и измерительной техники. Серьезной составной частью большинства научно-исследовательских работ являются измерения, позволяющие установить количественные соотношения и закономерности изучаемых явлений. Важность измерений в достижении научных результатов неоднократно отмечалась известными учеными: "Надо измерять все измеримое и делать измеримым то, что пока не поддается измерению" (Галилео Галилей); "Наука начинается с тех пор, как начинают измерять; точная наука немыслима без меры" (Д.И.Менделеев); "Искусство измерения является могущественным орудием, созданным человеческим разумом для проникновения в законы природы" (Б.С.Якоби). Прогресс в области измерений способствовал и способствует многим новым открытиям, а достижения науки, в свою очередь, — совершенствованию методов и средств измерений (например, благодаря использованию лазеров, микроэлектроники и т.п.).

При проведении экспертиз важным условием успеха является возможность формализовать информацию, не поддающуюся количественному измерению, так, чтобы помочь принимающему решение выбрать из множества действий одно. Поэтому в вопросах, связанных с теорией измерений, основное место отводится понятию шкалы измерения. В зависимости от того, по какой шкале идет измерение, экспертные оценки содержат больший или меньший объем информации и обладают различной способностью к математической формализации.

Типы шкал

Шкалы наименований или классификации используются для описания принадлежности объектов к определенным классам. Всем объектам одного и того же класса присваивается одно и то же число, объектам разных классов — разные.

Здесь наблюдаются только два отношения: "равно" и "не равно". Следовательно, допустимы любые преобразования лишь бы одинаковые объекты были поименованы одинаковыми символами (числами, буквами, словами), а разные объекты имели бы разные имена. Этим способом фиксируются такие характеристики, как собственные имена людей, их национальность, названия населенных пунктов и т.п.

Шкала порядка применяется для измерения упорядочения объектов по единичному или совокупности признаков. Числа в шкале порядка отражают только порядок следования объектов и не дают возможности сказать, на сколько или во сколько один объект предпочтительнее другого.

Допустимыми преобразованиями для данного типа шкалы являются все монотонные преобразования, т.е. такие, которые не нарушают порядок следования значений измеряемых величин. Такие шкалы появляются, например, в результате сравнения тел по твердости. Записи "1; 2; 3" и "5,3; 12,5; 109,2" содержат одинаковую информацию о том, что первое тело самое твердое, второе менее твердое, а третье — самое мягкое. И никакой информации о том, во сколько раз одно тверже другого, на сколько единиц оно тверже и т.д., в этих записях нет, и полагаться на конкретные значения чисел, на их отношения или разности нельзя.

Разновидностью шкалы порядка является шкала рангов, где используются только числа, идущие подряд от 1 вверх по возрастанию. Если среди измеряемых объектов одинаковых нет, то ранговое место каждого объекта в протоколе будет указано одним из целых чисел от 1 до. При одинаковом значении измеряемого свойства уобъектов, занимающих порядковые места с-го по-е, их ранги будут обозначены одинаковым числом, равным их "среднему" рангу, где,.

Такая разновидность шкалы порядка называется "нормированной шкалой рангов".

К типу шкал порядка относится и широко используемая шкала баллов. При этом используются целые числа в ограниченном диапозоне их значений: от 1 до 5 в системе образования, от 0 до 6 или до 10 в спорте и т.д. В любом из этих случаев протокол содержит информацию только о трех эмпирических отношениях: "<", ">" и "=".

Шкала интервалов применяется для отображения величины различия между свойствами объектов (измерение температуры по Фаренгейту и Цельсию). Шкала может иметь произвольные масштаб и точки отсчета.

Здесь между протоколами идопустимы линейные преобразования:, где— любое положительное число, аможет быть как положительным, так и отрицательным. Это значит, что в разных протоколах может использоваться разный масштаб единиц (a) и разные начала отсчета (b). Примером шкал этого типа могут быть шкалы для измерения температуры. Если в протоколе указаны градусы, но не говорится, в какой шкале (Цельсия, Кельвина и т.д.), то во избежание недоразумений при описании закономерностей можно использовать только отношения интервалов, так как при любых значенияхисохраняется равенство

Если записи в протоколе сопровождаются информацией о том, какие именно градусы имеются в виду (например, " "), то мы имеем дело с протоколом в абсолютной шкале.

Шкала отношений используется, например, для измерения массы, длины, веса. В этой шкале числа отражают отношения свойств объектов, т.е. во сколько раз свойство одного объекта превосходит свойство другого.

Между разными протоколами, фиксирующими один и тот же эмпирический факт на разных языках, при этом типе шкалы должно выполняться соотношение: , где— любое положительное число. Один и тот же эмпирический смысл имеют протоколы "16 кг", "16000 г", <0,016 т" и т.д. От любой записи можно перейти к любой другой, подобрав соответствующий множитель "". Этот тип шкалы удобен для измерения весов, длин и т.д. Если нам неизвестно, в каких именно единицах записаны веса тел в разных протоколах, то мы можем полагаться только на отношение весов двух тел: например, тело с весом 10 единиц в два раза тяжелее тела с весом 5 единиц вне зависимости от того, что было взято за единицу — тонна или грамм. Инвариантность отношений отражена в названии шкалы данного типа. Если же в протоколе указана единица веса, то такой протокол отражает свойства тел в абсолютной шкале.

Шкала разностей используется для измерения свойств объектов при необходимости указания, на сколько один объект превосходит другой по одному или нескольким признакам. Является частным случаем шкалы интервалов при выборе единицы масштаба.

Абсолютная шкала — частный случай шкалы интервалов. В ней обозначается нулевая точка отсчета и единичный масштаб. Применяется для измерения количества объектов.

Допустимое преобразование для шкал данного типа представляет собой тождество, т.е. если на одном языке в протоколе записано " ", а на другом языке "", то между ними должно выполняться простое соотношение:. Этот тип шкалы удобен для записи количества элементов в некотором конечном множестве. Если, пересчитав количество яблок, один эксперт запишет в протоколе "6", а другой — "VI", то нам достаточно знать, что "6" и "VI" означают одно и то же, т.е., что между этими записями существует тождественное отношение:.

Методы измерений

Ранжирование. При ранжировании эксперт располагает объекты в порядке предпочтения, руководствуясь одним или несколькими показателями сравнения. Парная оценка или метод парных сравнений представляет собой процедуру установления предпочтений объектов при сравнении всех возможных пар. Непосредственная оценка представляет собой процедуру приписывания объектам числовых значений по шкале интервалов. Эквивалентным объектам приписывается одно и то же число. Этот метод может быть осуществлен только при полной информированности экспертов о свойствах объектов. Вместо числовой оси может использоваться балльная оценка. Последовательное сравнение включает в себя ранжирование и непосредственную оценку.

Методы проведения групповой экспертизы

Методы проведения групповых экспертиз делятся на:

• очные и заочные;

• индивидуальные и коллективные;

• с обратной связью и без обратной связи.

При очном методе проведения экспертизы эксперт работает в присутствии организатора исследования. Эта необходимость может возникнуть, если задача поставлена недостаточно четко и нуждается в уточнении, а также если задача очень сложна. Эксперт может обратиться к организатору за разъяснениями.

При коллективном методе проведения экспертизы поставленная проблема решается сообща, "за круглым столом". При индивидуальном — каждый эксперт оценивает проблему, исходя из личного опыта и убеждений. Экспертиза с обратной связью (метод Дельфы) предусматривает проведение нескольких туров опроса и анонимное анкетирование. После каждого тура экспертные оценки обрабатываются, и результаты обработки сообщаются экспертам. Метод без обратной связи предусматривает один тур опроса при получении удовлетворительных результатов.

Каждый метод имеет ряд достоинств и недостатков, и при выборе определенного метода необходимо хорошо взвесить все его положительные и отрицательные стороны.

Коротко о достоинствах и недостатках каждого метода.

Для проведения очного опроса требуется больше времени, т.к. организатор экспертизы работает с каждым участником лично, но при сложности поставленной задачи это компенсируется большей точностью полученных результатов.

При проведении экспертизы методом экспертных комиссий группа специалистов коллективно оценивает исследуемую проблему. В этих условиях на группу может быть оказано давление одним из авторитетных ее членов, который способен лучше, чем другие, отстаивать свое мнение. Но в этом случае вероятность получения решения поставленной задачи больше. Этот метод рекомендуется при необходимости найти решение в кратчайшие сроки.

Проведение экспертизы методом Дельфы связано с большими затратами времени, т.к. в этом случае необходимо провести несколько туров. Но оглашение результатов предыдущего тура и последующий опрос позволяет добиться уменьшения диапазона разброса в индивидуальных ответах и сблизить точки зрения. Работа заканчивается, когда достигнута желаемая сходимость ответов экспертов. Опыт показывает, что чаще всего достаточно бывает провести четыре тура. Метод применяется обычно в прогнозировании, когда имеется большая степень неопределенности.

Экспертиза без обратной связи может проводиться при хорошей информированности экспертов в области поставленной задачи.

Классификация методов построения функции принадлежности

В основании всякой теории из любой области естествознания лежит очень важное, основополагающее для ее построения понятие элементарного объекта. Например, для механики — это материальная точка, для электродинамики — вектор напряженности поля. Для теории нечетких множеств основополагающим понятием является понятие нечеткого множества, которое характеризуется функцией принадлежности. Посредством нечеткого множества можно строго описывать присущие языку человека расплывчатые элементы, без формализации которых нет надежды существенно продвинуться вперед в моделировании интеллектуальных процессов. Но основной трудностью, мешающей интенсивному применению теории нечетких множеств при решении практических задач, является то, что функция принадлежности должна быть задана вне самой теории и, следовательно, ее адекватность не может быть проверена средствами теории. В каждом существующем в настоящее время методе построения функции принадлежности формулируются свои требования и обоснования к выбору именно такого построения.

Л.Заде предложил оценивать степень принадлежности числами из отрезка . Фиксирование конкретных значений при этом носит субъективный характер. С одной стороны, для экспертных методов важным является характер измерений (первичный или производный) и тип шкалы, в которой получают информацию от эксперта и которая определяет допустимый вид операций, принимаемых к экспертной оценке. С другой стороны, имеются два типа свойств: те, которые можно непосредственно измерить, и те, которые являются качественными и требуют попарного сравнения объектов, обладающих оцениваемым свойством, чтобы определить их место по отношению к рассматриваемому понятию.

Существует ряд методов построения по экспертным оценкам функции принадлежности нечеткого множества. Можно выделить две группы методов: прямые и косвенные методы.

Прямые методы определяются тем, что эксперт непосредственно задает правила определения значений функции принадлежности, характеризующей данное понятие. Эти значения согласуются с его предпочтениями на множестве объектов следующим образом:

1. для любых ,тогда и только тогда, еслипредпочтительнее, т.е. в большей степени характеризуется понятием;

2. для любых ,тогда и только тогда, еслиибезразличны относительно понятия.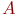

Примеры прямых методов: непосредственное задание функции принадлежности таблицей, формулой, перечислением. Заде обосновывает назначение прямого метода следующим образом: "По своей природе оценка является приближением. Во многих случаях достаточна весьма приблизительная характеризация набора данных, поскольку в большинстве основных задач, решаемых человеком, не требуется высокая точность. Человеческий мозг использует допустимость такой неточности, кодируя информацию, достаточную для решения задачи, элементами нечетких множеств, которые приближенно описывают исходные данные. Поток информации, поступающий в мозг через органы зрения, слуха, осязания и др., суживается таким образом в тонкую струйку информации, необходимой для решения поставленной задачи с минимальной степенью точности".

В косвенных методах значения функции принадлежности выбираются таким образом, чтобы удовлетворять заранее сформулированным условиям. Экспертная информация является только исходными данными для дальнейшей обработки. Дополнительные условия могут налагаться как на вид получаемой информации, так и на процедуру обработки. Примерами дополнительных условий могут служить следующие: функция принадлежности должна отражать близость к заранее выделенному эталону; объекты множества являются точками в параметрическом пространстве; результатом процедуры обработки должна быть функция принадлежности, удовлетворяющая условиям интервальной шкалы; при попарном сравнении объектов, если один объект оценивается враз сильнее, чем другой, то второй объект оценивается только враз сильнее, чем первый, и т.д.

Как правило, прямые методы используются для описания понятий, которые характеризуются измеримыми свойствами, такими как высота, рост, вес, объем. В этом случае удобно непосредственное задание значений степени принадлежности. К прямым методам можно отнести методы, основанные на вероятностной трактовке функции принадлежности , т.е. вероятности того, что объектбудет отнесен к множеству, которое характеризует понятие.

Если гарантируется, что люди далеки от случайных ошибок и работают как "надежные и правильные приборы", то можно спрашивать их непосредственно о значениях принадлежности. Однако имеются искажения, например, субъективная тенденция сдвигать оценки объектов в направлении концов оценочной шкалы. Следовательно, прямые измерения, основанные на непосредственном определении принадлежности, должны использоваться только в том случае, когда такие ошибки незначительны или маловероятны.

Косвенные методы основаны на более пессимистических представлениях о людях как об "измерительных приборах". Рассмотрим, например, понятие "КРАСОТА", которое, в отличие от понятий "ДЛИНА" или "ВЫСОТА", — сложное и трудно формализуемое. Практически не существует универсальных элементарных измеримых свойств, через которые определяется красота. В таких случаях используются только ранговые измерения при попарном сравнении объектов. Косвенные методы более трудоемки, чем прямые, но их преимущество — в стойкости по отношению к искажениям в ответе. Для косвенных методов можно выдвинуть условие "безоговорочного экстремума": при определении степени принадлежности множество исследуемых объектов должно содержать, по крайней мере, два объекта, численные представления которых на интервале принимают значенияи, соответственно. Итак, нами выделены две основные группы методов построения функции принадлежности:прямые и косвенные. Однако, функция принадлежности может отражать как мнение группы экспертов, так и мнение одного эксперта. Следовательно, возможны, по крайней мере, четыре группы методов: прямые и косвенные для одного эксперта, прямые и косвенные для группы экспертов. Кроме этого, необходимо рассмотреть методы построения функции принадлежности терм-множеств.

Методы построения функции принадлежности. Обзор основных методов

Прямые методы для одного эксперта

Прямые методы для одного эксперта состоят в непосредственном задании функции, позволяющей вычислять значения. Например, пусть переменная "ВОЗРАСТ" принимает значения из интервала . Слово "МОЛОДОЙ" можно интерпретировать как имя нечеткого подмножества, которое характеризуется функцией совместимости. Таким образом, степень, с которой численное значение возраста, скажем, совместимо с понятием "МОЛОДОЙ", есть, в то время как совместимостьис тем же понятием естьисоответственно.

Рассмотрим предложенный Осгудом метод семантических дифференциалов. Практически в любой области можно получить множество шкал оценок, используя следующую процедуру:

1. определить список свойств, по которым оценивается понятие (объект);

2. найти в этом списке полярные свойства и сформировать полярную шкалу;

3. для каждой пары полюсов оценить, в какой степени введенное понятие обладает положительным свойством.

Совокупность оценок по шкалам была названа профилем понятия. Следовательно, вектор с координатами, изменяющимися отдо, также называется профилем. Профиль есть нечеткое подмножество положительного списка свойств или шкал.

Пример. В задаче распознавания лиц можно выделить следующие шкалы:

	Высота лба	Низкий-широкий
	Профиль носа	Горбатый-курносый
	Длина носа	Короткий-длинный
	Разрез глаз	Узкие-широкие
	Цвет глаз	Темные-светлые
	Форма подбородка	Остроконечный-квадратный
	Толщина губ	Тонкие-толстые
	Цвет лица	Смуглое-светлое
	Очертание лица	Овальное-квадратное

Светлое квадратное лицо, у которого чрезвычайно широкий лоб, курносый длинный нос, широкие светлые глаза, остроконечный подбородок, может быть определено как нечеткое множество .

Способ вычисления частичной принадлежности друг другу строгих множеств. Пусть покрытиемобычного множестваявляется любая совокупность обычных подмножествмножестватаких, что. В крайнем случае, когда для любых,, имеет место разбиение. Предположим, что имеется, тогдаможет рассматриваться как нечеткое подмножествос функцией принадлежности

где — мощность множества.

Пример. Пусть,,,,,,. Тогда, рассматриваякак нечеткое подмножество, можно написать

Любое решение задачи многоцелевой оптимизации можно рассматривать как нечеткое подмножество значений целевой функции следующим образом. Пусть — целевые функции, где, и пусть требуется решить задачудля всех. Пусть— максимальное значение функциии— множество целевых функций, тогда любое значениев области определенияможно рассматривать как нечеткое множество нас вектором значений принадлежности

Косвенные методы для одного эксперта

В обыденной жизни мы часто сталкиваемся со случаями, когда не существует элементарных измеримых свойств и признаков, которые определяют интересующие нас понятия, например, красоту, интеллектуальность. Бывает трудно проранжировать степень проявления свойства у рассматриваемых элементов. Так как степени принадлежности рассматриваются на данном реальном множестве, а не в абсолютном смысле, то интенсивность принадлежности можно определять, исходя из попарных сравнений рассматриваемых элементов.

Среди косвенных методовопределения функции принадлежности наибольшее распространение получилметод парных сравнений Саати. Сложность использования этого метода заключается в необходимости нахождения собственного вектора матрицы парных сравнений, которая задается с помощью специально предложенной шкалы. Причем эти сложности увеличиваются с ростом размерности универсального множества, на которой задается лингвистический терм.

Мы рассмотрим метод, также использующий матрицу парных сравнений элементов универсального множества. Но, в отличие от метода Саати, он не требует нахождения собственного вектора матрицы, т.е. освобождает исследователя от трудоемких процедур решения характеристических уравнений.

Пусть — некоторое свойство, которое рассматривается как лингвистический терм. Нечеткое множество, с помощью которого формализуется терм, представляет собой совокупность пар:

где — универсальное множество, на котором задается нечеткое множество. Задача состоит в том, чтобы определить значениядля всех. Совокупность этих значений и будет составлять неизвестную функцию принадлежности.

Метод, который предлагается для решения поставленной проблемы, базируется на идее распределения степеней принадлежности элементов универсального множества согласно с их рангами. Эта идея раньше использовалась в теории структурного анализа систем, где рассмотрены различные способы определения рангов элементов.

В нашем случае под рангом элемента будем понимать число, которое характеризует значимость этого элемента в формировании свойства, описываемого нечетким термом. Допускаем, что выполняется правило:чем больший ранг элемента, тем больше степень принадлежности.

Для последующих построений введем такие обозначения: ,. Тогда правило распределения степеней принадлежности можно задать в виде системы соотношений:

Используя данные соотношения, легко определить степени принадлежности всех элементов универсального множества через степень принадлежности опорного элемента.

Если опорным является элемент с принадлежностью, то

Учитывая условие нормирования, находим:

Полученные формулы дают возможность вычислять степени принадлежности элементов к нечеткому термудвумя независимыми путями:

1. по абсолютным оценкам уровней , которые определяются согласно методикам, предложенным в теории структурного анализа систем;

2. по относительным оценкам рангов , которые образуют матрицу.

Эта матрица обладает следующими свойствами:

а) она диагональная, т.е.

б) ее элементы, которые симметричны относительно главной диагонали, связаны зависимостью

в) она транзитивна, т.е. .

Наличие этих свойств приводит к тому, что при известных элементах одной строки матрицы легко определить элементы всех других строк. Если известна-я строка, т.е. элементы,, то произвольный элементнаходится так:

Поскольку матрица может быть интерпретирована как матрица парных сравнений рангов, то для экспертных оценок элементов этой матрицы можно использовать 9 балльную шкалу Саати. В нашем случае шкала формируется так:

Числовая оценка	Качественная оценка (сравнение и)
1	отсутствие преимущества над
3	слабое преимущество над
5	существенное преимущество над
7	явное преимущество над
9	абсолютное преимущество над
2, 4, 6, 8	промежуточные сравнительные оценки

Таким образом, с помощью полученных формул экспертные знания о рангах элементов или их парные сравнения преобразуются в функцию принадлежности нечеткого терма.

Скала предлагает общий метод варьирования прототипов получения численного значения функции принадлежности. Пусть имеется прототип (или идеальный объект), описание которого можно деформировать изменением параметров. Если дан некоторый объект, то, варьируя параметры, можно добиться наибольшего соответствия прототипа и объекта. Вводится мера сходства между объектоми прототипом:.

Для более точного измерения сходства объекта с разными прототипами вводится штрафная функция . Далее строится функция:

Так как прототип полностью соответствует самому себе, то . Численные значения функции принадлежности вычисляются по формуле

Прямые методы для группы экспертов

При интерпретации степени принадлежности как вероятности было предложено получать функции принадлежности для нескольких классов понятий расчетным путем, используя равенство, где условная вероятность определяется по формуле Байеса:

причем

— число случаев при значении параметра, когда верной оказалась-я гипотеза.

Я.Я.Осис предложил следующую методику оценки функции принадлежности. Первоначально определяется то максимальное количество классов, которое может быть описано данным набором параметров. Для каждого элемента значение функции принадлежности классадополняет до единицы значения функции принадлежности класса(в случае двух классов). Таким образом, система должна состоять из классов, представляющих противоположные события. Сумма значений функции принадлежности произвольного элементак системе таких классов будет равна единице. Если число классов и их состав четко не определены, то необходимо вводить условный класс, включающий те классы, которые не выявлены. Далее эксперты оценивают в процентах при данном состояниистепень проявления каждого класса из названного перечня.

Однако в некоторых случаях мнение эксперта очень трудно выразить в процентах, поэтому более приемлемым способом оценки функции принадлежности будет метод опроса, который состоит в следующем. Оцениваемое состояние предъявляется большому числу экспертов, и каждый имеет один голос. Он должен однозначно отдать предпочтение одному из классов заранее известного перечня. Значение функции принадлежности вычисляется по формуле , где— число экспертов, участвовавших в эксперименте, и— число экспертов, проголосовавших за класс.

Пример. Пусть в результате переписи населения в некоторой области с численностью жителейполучено множество значений возраста. Пусть— число людей, имеющих возрасти утверждающих, что являются молодыми. Пусть— действительное число людей, имеющих возраст; тогда. Можно считать, что понятие "МОЛОДОЙ" описывается нечетким множеством нас функцией принадлежности. Очевидно, что для малых значений возраста, следовательно,. Однако, не всесчитают себя молодыми, следовательно,. Длячислодолжно быть очень маленьким.

Косвенные методы для группы экспертов

А.П.Шер предлагает способ определения функции принадлежности на основе интервальных оценок. Пусть интервал отражает мнение-го эксперта,(), о значении-го () признака оцениваемого понятия. Тогда полным описанием этого понятия-м экспертом является гиперпараллелепипед. Приводится процедура, позволяющая вычислять коэффициенты компетентности экспертов, а также сводить исходную "размытую" функцию (усредненные экспертные оценки) к характеристической функции неразмытого, четкого множества. Алгоритм следующий:

1. Рассматривая для каждого признака 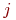все интервалы, предложенные экспертами, находим связанное покрытие их объединения, состоящее из непересекающихся интервалов, концами которых являются только концы исходных интервалов:

2. Образуем на основе полученных покрытий непересекающиеся гиперпараллелепипеды:

3. Вычисляем для .

4. Полагаем номер итерации .

5. Вводим коэффициенты компетентности

6. Вычисляем приближение функции принадлежности при нормированных , т.е.:

7. Вычисляем функционал рассогласования мнения -го эксперта с мнением экспертного совета на-й итерации:

8. Вычисляем

9. Присваиваем .

10. Вычисляем

11. Если величина близка к нулю, то вычисления прекращаем и приближением функции принадлежности считаем, в противном случае возвращаемся к шагу 6.

Опишем кратко косвенный метод, предложенный З.А.Киквидзе. Пусть— универсальное множество,— понятие, общее название элементов. Задача определения нечеткого подмножества, описывающего понятие, решается путем опроса экспертов. Каждый эксперт() выделяет измножество элементов, по его мнению, соответствующих понятию. Ранжируя все элементы множествапо предпочтению в смысле соответствия понятию, каждый эксперт упорядочивает, используя отношение порядкаили. Отношениеуказывает на одинаковую степень предпочтения между любыми элементами. Предполагается, что эксперты могут поставить коэффициенты степени предпочтенияперед элементами в упорядоченной последовательности, усиливая или ослабляя отношение предпочтения. Вводится расстояние между элементами указанной последовательности:

Здесь ,— порядковые номера элементов в упорядочении. Расстояние вычисляется через первый в упорядочении элемент:

Эта разность показывает, насколько предпочтительнее по сравнению с. При решении задачи взвешивания предпочтительности элементов множествапредполагается, что разность между весамипропорциональна разности:. Когда, формула превращается в рекуррентную формулу, и задача сводится к определению веса первого элемента. При использовании рекуррентных формул вес последнего элемента должен отличаться от нуля. Например, в качествеможно выбрать. На основании всехдляопределяется значение; это и есть степень принадлежности элементанекоторому нечеткому множеству с общим названием.

Зиммерман предлагает метод, сочетающий преимущества косвенных методовв их простоте и стойкости к искажениям ответов экспертов и преимуществапрямых методов, позволяющих получить непосредственно значения степени принадлежности. Выборку объектов необходимо проводить так, чтобы достаточно равномерно представить степень принадлежности отдопо отношению к рассматриваемому нечеткому множеству. Эта выборка должна удовлетворять условию безоговорочного экстремума, т.е. должна содержать, по крайней мере, два объекта, значения функции принадлежности на которых имеют определенностьи(все эксперты приписывают эти числа экстремумам). Далее, когда множество подходящих объектов отобрано, эксперты опрашиваются о степенях принадлежности в процентной шкале. Оценка позиции по шкале каждого объекта определяется посредством медианы из распределений значений принадлежности. В качестве процедуры шкалирования используется метод, основанный на законе Терстона об измерении категорий. Процедура, требующая отсортировкиобъектов вкатегории на некотором континууме свойствэкспертами, дает распределение частоты для каждого объекта по категориям. Средние значения границ категорий, полученные методом наименьших квадратов, позволяют определить значения оценок объектов на шкале.

Методы построения терм-множеств

Считается, что для практических задач достаточно наличия нечеткого языка с фиксированным конечным словарем — ограничение не слишком сильное с точки зрения практического использования. Лингвистическая переменная , используемая при формализации задач принятия решения, на практике, как правило, имеет базовоетерм-множество, состоящее из 2—10 термов. Каждый терм описывается нечетким подмножеством множества значенийнекоторой базовой переменнойи рассматривается как лингвистическое значение. Предполагается, что объединение всех этих элементов терм-множества покрывает полностью. Это гарантирует, что любой элементописывается некоторым.

Существует способ построения частотных оценок {"редко", "часто", "иногда",...}, который основан на предположении о том, что словоупотребляется человеком не для обозначения зарегистрированной частоты появления факта, а для обозначения относительного числа событий в прошлой деятельности человека, когда рассматривалась такая же частота. Каждомуставится в соответствие нечеткое подмножество интервала. Функции принадлежностиполучаются на основании психологического эксперимента следующим образом: группе испытуемых предъявляется набор стимулов (оценок частоты) и шкала изкатегорий, упорядоченных по степени интенсивности частоты от наименьшейдо наибольшей; испытуемым предлагается разбить стимулы наклассов согласно интенсивности частоты, независимо оценивая каждый стимул и помещая в любую категорию любое число стимулов. Каждому числуиз,, ставятся в соответствие степени употребления группой испытуемых словадля обозначения категории. Значения функции принадлежности определяются в результате нормирования:.

Предложенная методика оправдана следующим: выбор обозначения категории не отражается сколь-нибудь значительно на проведении испытания. Во-первых, число категорий (деление шкалы) не влияет кардинально на результаты эксперимента, в котором производится шкалирование субъективных ощущений. Во-вторых, шкала из категорий является шкалой равно кажущихся интервалов, поскольку предполагается, что ее деления отстоят на психологическом континууме на равных интервалах.

Естественным шагом при построении функций принадлежности элементов терм-множества лингвистической переменной является построение одновременно всех функций принадлежности этого терм-множества, сгруппированных в так называемое отношение моделирования . Процесс построения состоит в заполнении таблицы, где, например, для лингвистической переменной "РАССТОЯНИЕ" столбцы индексированы расстояниями в метрах, а строки — элементами терм-множества "ОЧЕНЬ БЛИЗКО", "БЛИЗКО",..., "ДАЛЕКО", "ОЧЕНЬ ДАЛЕКО". На пересечении соответствующей строки и столбца стоит степень сходства для испытуемого данных понятий в определенной семантической ситуации, например, насколько сходны понятия "БЛИЗКО" и "5 метров" в ситуации перебегания улицы перед быстро идущим транспортом. Расстояние берется от пешехода до машины и в данном случае является синонимом опасности. Вообще говоря, каждую клеточку таблицы можно заполнять отдельно, а потом, переставляя строки и столбцы, постараться сделать строки и столбцы унимодальными. Если это удается, то исходное терм-множество может быть использовано для построения нечеткой шкалы измерений, точками отсчета которой являются сами элементы терм-множества. Перевод в эту шкалу будет осуществляться с помощью минимаксного умножения строки, задающей исходную лингвистическую переменную в шкале метров, на отношение моделирования. Отношение сходства между элементами терм-множества, полученное с помощью умножения матрицына транспонированную, задает набор функций принадлежности элементов лингвистической шкалы в самой шкале, а отношениезадает набор функций принадлежности расстояний в метрах в метрической шкале.

Нечеткая логика

В сочетании слов "нечеткий" и "логика" есть что-то необычное. Логика в обычном смысле слова есть представление механизмов мышления, то, что никогда не может быть нечетким, но всегда строгим и формальным. Однако математики, исследовавшие эти механизмы мышления, заметили, что в действительности существует не одна логика (например, булева), а столько, сколько мы пожелаем, потому что все определяется выбором соответствующей системы аксиом. Конечно, как только аксиомы выбраны, все утверждения, построенные на их основе, должны быть строго, без противоречий увязаны друг с другом согласно правилам, установленным в этой системе аксиом.

Человеческое мышление — это совмещение интуиции и строгости, которое, с одной стороны, рассматривает мир в целом или по аналогии, а с другой стороны — логически и последовательно и, значит, представляет собой нечеткий механизм. Законы мышления, которые мы захотели бы включить в программы компьютеров, должны быть обязательно формальными; законы мышления, проявляемые в диалоге человека с человеком — нечеткие. Можем ли мы поэтому утверждать, что нечеткая логика может быть хорошо приспособлена к человеческому диалогу? Да — если математическое обеспечение, разработанное с учетом нечеткой логики, станет операционным и сможет быть технически реализовано, то человеко-машинное общение станет намного более удобным, быстрым и лучше приспособленным к решению проблем.

Термин " нечеткая логика " используется обычно в двух различных значениях. В узком смысле, нечеткая логика — это логическое исчисление, являющееся расширением многозначной логики. В ее широком смысле, который сегодня является преобладающим в использовании, нечеткая логика равнозначна теории нечетких множеств. С этой точки зрения, нечеткая логика в узком смысле является разделом нечеткой логики в широком смысле.

Определение. Любая нечеткая переменная характеризуется тройкой

где — название переменной,— универсальное множество,— нечеткое подмножество множества, представляющее собой нечеткое ограничение на значение переменной, обусловленное.

Используя аналогию с саквояжем, нечеткую переменную можно уподобить саквояжу с ярлыком, имеющим "мягкие" стенки. Тогда — надпись на ярлыке (название саквояжа),— список предметов, которые в принципе можно поместить в саквояж, а— часть этого списка, где для каждого предметауказано число, характеризующее степень легкости, с которой предмет можно поместить в саквояж.

Рассмотрим теперь различные подходы к определению основных операций над нечеткими переменными, а именно конъюнкции, дизъюнкции и отрицания. Данные операции являются основными для нечеткой логики в том смысле, что все ее конструкции основываются на этих операциях. В настоящее время в нечеткой логике в качестве операций конъюнкции и дизъюнкции широко используют -нормы и-конормы, пришедшие внечеткую логику из теории вероятностных метрических пространств. Они достаточно хорошо изучены и лежат в основе многих формальных построений нечеткой логики. В то же время расширение области приложений нечеткой логики и возможностей нечеткого моделирования вызывает необходимость обобщения этих операций. Одно направление связано с ослаблением их аксиоматики с целью расширения инструментария нечеткого моделирования. Другое направление обобщения операций конъюнкции и дизъюнкции нечеткой логики связано с заменой множества значений принадлежности на линейно или частично упорядоченное множество лингвистических оценок правдоподобности. Эти обобщения основных операцийнечеткой логики, с одной стороны, вызываются необходимостью разработки экспертных систем, в которых значения истинности фактов и правил описываются экспертом или пользователем непосредственно в лингвистической шкале и носят качественный характер. С другой стороны, такие обобщения вызываются смещением направления активного развития нечеткой логики от моделирования количественных процессов, поддающихся измерению, к моделированию процессов мышления человека, где восприятие мира и принятие решений происходит на основе гранулирования информации и вычисления словами.

Естественным обобщением инволютивных операций отрицания нечеткой логики являются неиволютивные отрицания. Они представляют самостоятельный интерес и рассматриваются в нечеткой и других неклассических логиках. Необходимость исследования подобных операций отрицания вызывается также введением в рассмотрение обобщенных операций конъюнкции и дизъюнкции, связанных друг с другом с помощью операции отрицания.

Операции отрицания

Пусть множество значений функций принадлежности является линейно упорядоченным множеством с наименьшим0 и наибольшим 1 элементами. Примером может служить интервал вещественных чисел, шкала лингвистических оценок (например, L={"неправдоподобно", "малоправдоподобно", "средняя правдоподобность", "большая правдоподобность", "наверняка"}, шкала балльных оценок и др.

Определение. Операцией отрицания на называется функция , удовлетворяющая следующим условиям:

(О1) ;

(O2) .

В зависимости от выполнения на дополнительных условий, рассматриваются следующие типы отрицаний:

• Строгое отрицание: ;

• Квазистрогое отрицание: ;

• Инволюция: ;

• Обычное отрицание: ;

• Слабое отрицание: .

Слабое отрицание называется также интуиционистским отрицанием. Элемент избудет называться иволютивным элементом, если, в противном случае он будет называться неиволютивным. Отрицание будет называться неиволютивным, еслисодержит неиволютивные по этому отрицанию элементы.

Элемент , удовлетворяющий условию, называется фиксированной точкой. Этот элемент будет центральным элементом (фокусом). Очевидно, что если фиксированная точка существует, то она единственна.

Отрицание называется сжимающим в точке, если выполнено условие

Отрицание называется сжимающим на , если оно сжимающее в каждой точке множества.

Отрицание называется разжимающим в точке, если выполнено условие

Отрицание называется разжимающим на , если оно является разжимающим в каждой точке множества.

Теорема Для любого отрицания любая точкаявляется либо сжимающей, либо разжимающей.

Доказательство Пусть , тогда из условия (О2) получим, откуда следует либо, либо. Аналогично, изполучаем, и, следовательно, либо, либо

Следствие Элемент является иволютивным тогда и только тогда, если он одновременно сжимающий и разжимающий.

Используя математические методы, можно доказать, что элементы, порождаемые сжимающими и разжимающими отрицаниями в точках, представляют собой спирали, соответственно "закручиваемые внутрь" или "раскручиваемые наружу". Эти спирали либо бесконечные, либо в конечном случае имеют петлю на конце, состоящую из двух элементов, которые для сжимающих отрицаний могут совпадать, образуя неподвижную точку отрицания. Спирали, порождаемые разными элементами, либо вложены друг в друга, либо совпадают, начиная с некоторого элемента.

На рис. 8.1 даны примеры сжимающего и разжимающего в точке отрицания. Элементыпредставлены вершинами соответствующего графа и упорядочены снизу вверх, в частности,. Элементы y порождаются элементамитак, чтодлярис. 8.1(А) и длярис. 8.1(Б).

Рис. 8.1.

Рассмотрим простейшие примеры отрицаний. Во всех примерах предполагается, что содержит элементы, отличные от0 и 1.

Пример. "Все, что не истина и не ложь, является неопределенностью".

Рис. 8.2.

где — некоторый элемент изтакой, что. Это отрицание является сжимающим, ни обычным, ни слабым, с фиксированной точкой.

Пример. "Все, что не истина, есть ложь".

Рис. 8.3.

Это отрицание является обычным, разжимающим, квазистрогим, без фиксированной точки.

Пример. "Все, что не ложь, есть истина".

Рис. 8.4.

Это отрицание является слабым, разжимающим, квазистрогим, без фиксированной точки.

Пример. "Все или истина, или ложь".

Рис. 8.5.

где — некоторый элемент изтакой, что.

Это отрицание является разжимающим, ни обычным, ни слабым, без фиксированной точки. Некоторые подходы к формализации нечеткой логики, основанные на подобной интерпретации, сводят ее к двузначной, используя .

Пример. Пусть , где.

Рис. 8.6.

Это отрицание является иволютивным. При нечетном фиксированной точкой отрицания является элемент. Мера нечеткости на этом элементе принимает максимальное значение. При четномфиксированная точка отрицания отсутствует, фокус состоит из множества, имеющих максимальную нечеткость.

Операции конъюнкции и дизъюнкции

Как отмечалось на предыдущих лекциях, операции конъюнкции и, введенные Заде, обладают почти всеми свойствами соответствующих булевых операций. Это позволяет легко обобщать для нечеткого случая многие понятия "четкой" логики. Однако с других точек зрения эти операции являются ограничительными. Возможность рассмотрения более "мягких" операций конъюнкции и дизъюнкции обсуждал еще Заде в своих первых работах.

Целесообразность применения тех или иных операций конъюнкции и дизъюнкции в нечеткой логике может рассматриваться с разных позиций в зависимости от области приложения нечеткой логики.

Во-первых, эти операции интересны с точки зрения моделирования лингвистических связок "и" и "или", используемых человеком. С одной стороны, операции иявляются адекватными в порядковых шкалах, в которых обычно измеряются лингвистические оценки. Это обусловливает их широкое применение в нечетких лингвистических моделях. Однако, недостатком этих операций является то, что их результат равен значению одного операнда и не меняется при изменении значений второго операнда в определенном диапазоне величин. Например,для всех значений. Кроме того, в ряде экспериментальных работ было установлено, что операцииине являются достаточно удовлетворительными с точки зрения моделирования лингвистических связок. Это привело к появлению работ по разработке строго монотонных операций в порядковых шкалах, по настраиваемым на эксперта табличным операциям, а также стимулировало исследования по поиску новых операций конъюнкции и дизъюнкции.

Во-вторых, расширение класса операций конъюнкции и дизъюнкции было вызвано необходимостью построения достаточно общих математических моделей, которые могли бы с единых позиций рассматривать, например, вероятностные и многозначные логики, различные методы принятия решений, обработки данных и т.д. Подобное расширение произошло в результате введения в рассмотрение недистрибутивных операций конъюнкции и дизъюнкции, известных под названием -норм и-конорм.

Докажем, что условие дистрибутивности совместно с условиями монотонности и граничными условиями однозначно определяет операции Заде. Итак, пусть нам даны две операции и, удовлетворяющие следующим условиям:

1. Дистрибутивность:

2. Монотонность:

3. Граничные условия:

Из монотонности и граничных условий следует выполнение условий:

Далее выводится условие идемпотентности дизъюнкции:

И из

следует

Аналогично выводится

Установлено, что именно условие дистрибутивности является наиболее жестким ограничением на возможную форму операций конъюнкции и дизъюнкции. Удаление этого свойства из множества аксиом устраняет единственность операций ии дает возможность совершать построения широкого спектра нечетких связок. Свойство дистрибутивности очень важно в логике, так как оно дает возможность совершать эквивалентные преобразования логических форм из дизъюнктивной в конъюнктивную форму и обратно. Оно активно используется в процедурах минимизации логических функций, в процедурах логического вывода на основе принципа резолюции и т.п. Однако, во многих задачах такие преобразования логических форм не являются необходимыми, и поэтому оказалось, что свойство дистрибутивности может быть "довольно безболезненно" удалено из системы аксиом, определяющихнечеткие операции конъюнкции и дизъюнкции. Основной аксиомой для них является ассоциативность, и свойства этих операций во многом определяются общими свойствами ассоциативных функций и операций, активно изучающихся в математике.

Простейшими примерами недистрибутивных операций являются следующие -нормы и-конормы:

(минимум),

(максимум),

(произведение),

(вероятностная сумма),

(t-норма Лукасевича),

(t-конорма Лукасевича),

(сильное произведение),

(сильная сумма).

Для любых -норми-конормвыполняются следующие неравенства:

Таким образом, -нормыиявляются минимальной и максимальной границами для всех-норм. Аналогично,-конормыявляются минимальной и максимальной границами для всех-конорм. Эти неравенства очень важны для практического применения, так как они устанавливают границы возможного варьирования операций недистрибутивных конъюнкции и дизъюнкции.

В-третьих, рассмотрение логических операций конъюнкции и дизъюнкции как вещественных функций, являющихся компонентами нечетких моделей процессов и систем, естественно вызывает необходимость рассмотрения широкого класса таких функций, увеличивающих гибкость моделирования. По этим причинам, в ряде приложений нечеткой логики некоторые аксиомы -норм и-конорм также оказались ограничительными. В частности, параметрические классы данных операций имеют достаточно сложный вид, затрудняющий их аппаратную реализацию и оптимизацию нечетких моделей по параметрам этих операций. Сложность параметрических классов конъюнкций и дизъюнкций определяется способом генерации этих операций, который фактически определяется условием ассоциативности. С этой точки зрения свойство ассоциативности может рассматриваться как ограничительное. В то же время, свойство коммутативности операций конъюнкции и дизъюнкции может рассматриваться как необязательное ограничение на эти операции, так как в общем случае в нечетких моделях операнды данных операций могут характеризовать переменные, по-разному влияющие на результат. Свойства ассоциативности и коммутативности являются важными, например, в нечетких моделях многокритериального принятия решений, поскольку одним из разумных требований, накладываемых на процедуры принятия решений, является их независимость от порядка рассмотрения альтернатив и критериев. Но для систем нечеткого вывода эти свойства не всегда являются необходимыми, особенно когда позиции переменных в нечетких правилах и процедуры обработки правил фиксированы, а также когда число входных переменных не превышает двух, что бывает во многих реальных приложениях нечетких моделей. По этой причине из определениянечетких операций конъюнкции и дизъюнкции могут быть удалены свойства коммутативности и ассоциативности так же, как это было ранее сделано со свойствами дистрибутивности.

В качестве примера некоммутативных, неассоциативных операций дизъюнкции и конъюнкции можно привести следующие:

Понятие лингвистической переменной

Лингвистическая переменная отличается от числовой переменной тем, что ее значениями являются не числа, а слова или предложения в естественном или формальном языке. Поскольку слова в общем менее точны, чем числа, понятие лингвистической переменной дает возможность приближенно описывать явления, которые настолько сложны, что не поддаются описанию в общепринятых количественных терминах. В частности, нечеткое множество, которое представляет собой ограничение, связанное со значениями лингвистической переменной, можно рассматривать как совокупную характеристику различных подклассов элементов универсального множества. В этом смысле роль нечетких множеств аналогична той роли, которую играют слова и предложения в естественном языке. Например, прилагательное "КРАСИВЫЙ" отражает комплекс характеристик внешности индивидуума. Это прилагательное можно также рассматривать как название нечеткого множества, которое является ограничением, обусловленным нечеткой переменной "КРАСИВЫЙ". С этой точки зрения термины "ОЧЕНЬ КРАСИВЫЙ", "НЕКРАСИВЫЙ", "ЧЕРЕЗВЫЧАЙНО КРАСИВЫЙ", "ВПОЛНЕ КРАСИВЫЙ" и т.п. — названия нечетких множеств, образованных путем действия модификаторов "ОЧЕНЬ, НЕ, ЧЕРЕЗВЫЧАЙНО, ВПОЛНЕ" и т.п. на нечеткое множество "КРАСИВЫЙ". В сущности, эти нечеткие множества вместе с нечетким множеством "КРАСИВЫЙ" играют роль значений лингвистической переменной "ВНЕШНОСТЬ".

Важный аспект понятия лингвистической переменной состоит в том, что эта переменная более высокого порядка, чем нечеткая переменная, в том смысле, что значениями лингвистической переменной являются нечеткие переменные. Например, значениями лингвистической переменной "ВОЗРАСТ" могут быть: "МОЛОДОЙ, НЕМОЛОДОЙ, СТАРЫЙ, ОЧЕНЬ СТАРЫЙ, НЕ МОЛОДОЙ И НЕ СТАРЫЙ" и т.п. Каждое из этих значений является названием нечеткой переменной. Если — название нечеткой переменной, то ограничение, обусловленное этим названием, можно интерпретировать как смысл нечеткой переменной.

Другой важный аспект понятия лингвистической переменной состоит в том, что лингвистической переменной присущи два правила:

1. Cинтаксическое, которое может быть задано в форме грамматики, порождающей название значений переменной;

2. Cемантическое, которое определяет алгоритмическую процедуру для вычисления смысла каждого значения.

Определение. Лингвистическая переменная характеризуется набором свойств , в котором:

— название переменной;

обозначает терм-множество переменной , т.е. множество названий лингвистических значений переменной, причем каждое из таких значений является нечеткой переменнойсо значениями из универсального множествас базовой переменной;

— синтаксическое правило, порождающее названия значений переменной;

— семантическое правило, которое ставит в соответствие каждой нечеткой переменной ее смысл, т.е. нечеткое подмножествоуниверсального множества.

Конкретное название , порожденное синтаксическим правилом, называется термом. Терм, который состоит из одного слова или из нескольких слов, всегда фигурирующих вместе друг с другом, называется атомарным термом. Терм, который состоит из более чем одного атомарного терма, называется составным термом.

Пример. Рассмотрим лингвистическую переменную с именем "ТЕМПЕРАТУРА В КОМНАТЕ". Тогда оставшуюся четверку, можно определить так:

1. универсальное множество U=[5,35];

2. терм-множество T={"ХОЛОДНО", "КОМФОРТНО", "ЖАРКО"} с такими функциями принадлежностями:

3. синтаксическое правило , порождающее новые термы с использованием квантификаторов "и", "или", "не", "очень", "более-менее" и других;

4. будет являться процедурой, ставящей каждому новому терму в соответствие нечеткое множество из по правилам: если термыиимели функции принадлежностиисоответственно, то новые термы будут иметь следующие функции принадлежности, заданные в таблице:

Квантификатор	Функция принадлежности ( )
не
очень
более-менее
и
или

Графики функций принадлежности термов "холодно", "не очень холодно" и т.п. к лингвистической переменной "температура в комнате" показаны на рис. 9.1:

увеличить изображение Рис. 9.1.

В рассмотренном примере терм-множество состояло лишь из небольшого числа термов, так что целесообразно было просто перечислить элементы терм-множества и установить прямое соответствие между каждым элементом и его смыслом. В более общем случае, число элементов вможет быть бесконечным, и тогда как для порождения элементов множества, так и для вычисления их смысла необходимо применять алгоритм, а не просто процедуру перечисления.

Будем говорить, что лингвистическая переменная структурирована, если ее терм-множество и функцию, которая ставит в соответствие каждому элементу терм-множества его смысл, можно задать алгоритмически.

Пример. В качестве очень простой иллюстрации той роли, которую играют синтаксическое и семантическое правила в случае структурированной лингвистической переменной, рассмотрим переменную РОСТ, терм-множество которой можно записать в виде:

T(РОСТ)={ВЫСОКИЙ,ОЧЕНЬ ВЫСОКИЙ,ОЧЕНЬ-ОЧЕНЬ ВЫСОКИЙ,...}.

M(ВЫСОКИЙ)=

M(ОЧЕНЬ ВЫСОКИЙ)=(М(ВЫСОКИЙ))2, и т.д.

Лингвистическую переменную будем называть булевой, если ее термы являются булевыми комбинациями переменных вида и, где— лингвистическая неопределенность,— атомарный терм.

Пример. Пусть "ВОЗРАСТ" — булева лингвистическая переменная с терм-множеством вида

Т(ВОЗРАСТ)={МОЛОДОЙ, НЕМОЛОДОЙ, СТАРЫЙ, НЕСТАРЫЙ, ОЧЕНЬ МОЛОДОЙ, НЕ МОЛОДОЙ И НЕ СТАРЫЙ, МОЛОДОЙ ИЛИ НЕ ОЧЕНЬ СТАРЫЙ, ...}.

В этом примере имеется два атомарных терма — МОЛОДОЙ и СТАРЫЙ и одна неопределенность — ОЧЕНЬ.

Если отождествлять союз И с операцией пересечения нечетких множеств, ИЛИ — с операцией объединения нечетких множеств, отрицание НЕ — с операцией взятия дополнения и модификатор ОЧЕНЬ — с операцией концентрирования, то данная переменная будет полностью структурирована.

Лингвистические переменные истинности

В каждодневных разговорах мы часто характеризуем степень истинности утверждения посредством таких выражений, как "очень верно", "совершенно верно", "более или менее верно", "ложно", "абсолютно ложно" и т.д. Сходство между этими выражениями и значениями лингвистической переменной наводит на мысль о том, что в ситуациях, когда истинность или ложность утверждения определены недостаточно четко, может оказаться целесообразным трактовать ИСТИННОСТЬ как лингвистическую переменную, для которой ИСТИНО и ЛОЖНО — лишь два атомарных терма в терм-множестве этой переменной. Такую переменную будем называть лингвистической переменной истинности, а ее значения — лингвистическими значениями истинности.

Трактовка истинности как лингвистической переменной приводит к нечеткой лингвистической логике, которая совершенно отлична от обычной двузначной или даже многозначной логики. Такая нечеткая логика является основой того, что можно было бы назвать приближенными рассуждениями, т.е. видом рассуждений, в которых значения истинности и правила их вывода являются нечеткими, а не точными. Приближенные рассуждения во многом сродни тем, которыми пользуются люди в некорректно определенных или не поддающихся количественному описанию ситуациях. В самом деле, вполне возможно, что многие, если не большинство человеческих рассуждений по своей природе приближенны, а не точны.

В дальнейшем будем пользоваться термином "нечеткое высказывание" для обозначения утверждения вида " есть", где— название предмета, а— название нечеткого подмножества универсального множества, например, "Джон — молодой", "X — малый", "яблоко — красное" и т.п. Если интерпретироватькак нечеткий предикат, то утверждение "есть" можно перефразировать как "имеет свойство".

Будем полагать, что высказыванию типа " есть" соответствуют два нечетких подмножества:

1. — смысл , т.е. нечеткое подмножество с названиемуниверсального множества;

2. Значение истинности утверждения " есть", которое будем обозначатьи определять как возможно нечеткое подмножество универсального множества значений истинности. Будем предполагать, что.

Значение истинности, являющееся числом в , например, будем называтьчисловым значением истинности. Числовые значения истинности играют роль значений базовой переменной для лингвистической переменной ИСТИННОСТЬ. Лингвистические значения переменной ИСТИННОСТЬ будем называть лингвистическими значениями истинности. Более точно будем предполагать, что ИСТИННОСТЬ — название булевой лингвистической переменной, для которой атомарным является терм ИСТИННЫЙ, а терм ЛОЖНЫЙ определяется не как отрицание терма ИСТИННЫЙ, а как его зеркальное отображение относительно точки . Далее мы покажем, что такое определение значения ЛОЖНЫЙ является следствием его определения как значения истинности высказывания "есть не" при предположении, что значение истинности высказывания "есть" является ИСТИННЫМ.

Предполагается, что смысл первичного терма ИСТИННЫЙ является нечетким подмножеством интервала с функцией принадлежности типа

показанной на рис. 9.2

увеличить изображение Рис. 9.2.

Здесь точка является точкой перехода. Соответственно, для терма ЛОЖНЫЙ имеем

Логические связки в нечеткой лингвистической логике

Чтобы заложить основу для нечеткой лингвистической логики, необходимо расширить содержание таких логических операций, как отрицание, дизъюнкция, конъюнкция и импликация, применительно к высказываниям, которые имеют не числовые, а лингвистические значения истинности.

При рассмотрении этой проблемы полезно иметь в виду, что если — нечеткое подмножество универсального множестваи, то два следующих утверждения эквивалентны:

1. Степень принадлежности элемента нечеткому множествуесть.

2. Значение истинности нечеткого предиката " есть" также равно.

Таким образом, вопрос "Что является значением истинности высказывания " есть" И "есть", если заданы лингвистические значения истинности высказываний "есть" и "есть"?" аналогичен вопросу "Какова степень принадлежности элементамножеству, если заданы степени принадлежности элементамножествами?".

В частности, если — точка в, представляющая значение истинности высказывания "есть" (или просто), где— элемент универсального множества, то значение истинности высказывания "есть не" (или) определяется выражением

Предположим теперь, что — не точка в, нечеткое подмножество интервала, представленное в виде

Тогда получим

В частности, если значение истинности есть ИСТИННО, т.е.ИСТИННО, то значение истинности ЛОЖНО является значением истинности для высказывания.

Замечание Следует отметить, что если ИСТИННЫЙ , то функциябудет интерпретироваться термом НЕ ИСТИННЫЙ, а функция— термом ЛОЖНЫЙ, что в принципе не одно и то же (см.рис. 9.2).

То же самое относится к лингвистическим неопределенностям. Например, если ИСТИННЫЙ , то значение терма ОЧЕНЬ ИСТИННЫЙ равно(см.рис. 9.3).

С другой стороны, если значение истинности высказывания есть, то функциябудет выражать значение истинности высказывания "очень".

Рис. 9.3.

Перейдем к бинарным связкам. Пусть и— лингвистические значения истинности высказыванийисоответственно. В случае, когдаи— точечные оценки, имеем:

где операции исводятся к операциям нечеткой логики (см.предыдущую лекцию).

Если и— лингвистические значения истинности, заданные функциями

то, согласно принципу обобщения, конъюнкция и дизъюнкция будут вычисляться по следующим формулам:

Замечание Важно четко понимать разницу между связкой И (ИЛИ) в терме, например, ИСТИННЫЙ И (ИЛИ) НЕ ИСТИННЫЙ и символом () в высказывании ИСТИННЫЙ() НЕ ИСТИННЫЙ. В первом случае, нас интересует смысл терма ИСТИННЫЙ И (ИЛИ) НЕ ИСТИННЫЙ, и связка И (ИЛИ) определяется отношением

(ИСТИННЫЙ И (ИЛИ) НЕ ИСТИННЫЙ)=

= (ИСТИННЫЙ)()(НЕ ИСТИННЫЙ),

где — смысл терма. Напротив, в случае терма ИСТИННЫЙ() НЕ ИСТИННЫЙ нас в основном интересует значение истинности высказывания ИСТИННЫЙНЕ ИСТИННЫЙ, которое получается из равенства

(A И (ИЛИ) B) = .

Значения истинности НЕИЗВЕСТНО и НЕ ОПРЕДЕЛЕНО

Среди возможных значений истинности лингвистической переменной ИСТИННОСТЬ два значения привлекают особое внимание, а именно пустое множество и единичный интервал, которые соответствуют наименьшему и наибольшему элементам (по отношению включения) решетки нечетких подмножеств интервала. Важность именно этих значений истинности обусловлена тем, что их можно интерпретировать как значения истинности НЕ ОПРЕДЕЛЕНО и НЕИЗВЕСТНО соответственно.

Важно четко понимать разницу между и. Когда мы говорим, что степень принадлежности точкимножествуесть, мы имеем в виду, что функция принадлежностине определена в точке. Предположим, например, что— множество действительных чисел, а— функция, определенная на множестве целых чисел, причем, есличетное, и, еслинечетное. Тогда степень принадлежности числамножествуесть, а не.

С другой стороны, если бы была определена на множестве действительных чисел итогда и только тогда, если— четное число, то степень принадлежности числа 1,5 множествубыла бы равна.

Понятие значения истинности НЕИЗВЕСТНО в сочетании с принципом обобщения помогает уяснить некоторые понятия и соотношения обычных двухзначных и трехзначных логик. Эти логики можно рассматривать как вырожденные случаи нечеткой логики, в которой значением истинности НЕИЗВЕСТНО является весь единичный интервал, а не множество .

Формализация понятия нечеткого алгоритма

Различные понятия, нечеткие по своей природе, могут быть формально описаны посредством нечетких множеств. Нечеткая логика, например, позволяет формализовать простые логические связки нечетких переменных с помощью нечетких высказываний. Для описания же сложных соотношений между переменными удобно использовать нечеткие алгоритмы.

Под алгоритмом понимается точно определенное правило действий (программа), для которого задано указание, как и в какой последовательности это правило необходимо применять к исходным данным задачи, чтобы получить ее решение. Характеристиками алгоритма являются:

а) детерминированность — однозначность результата процесса при неизменных исходных данных;

б) дискретность определяемого алгоритмом процесса — расчлененность его на отдельные элементарные акты, возможность выполнения которых человеком или машиной не вызывает сомнения;

в) массовость — исходные данные для алгоритма можно выбрать из некоторого множества данных, т.е. алгоритм должен обеспечить решение любой задачи из класса однотипных задач.

Нечеткий же алгоритм , упрощенно говоря, определяется упорядоченным множеством нечетких инструкций (нечетких высказываний), которые содержат понятия, формализуемые нечеткими множествами.

Под нечеткими инструкциями понимаются инструкции, содержащие нечеткое понятие, например, "пройти около 100 метров", а под машинными — инструкции, не содержащие никаких нечетких понятий: "пройти 100 метров". Здесь и далее четкие инструкции мы будем называть машинными, чтобы подчеркнуть возможность моделирования нечетких алгоритмов на ЭВМ, воспринимающих только чтение инструкций.

Приведем точное определение нечеткого алгоритма. Для формулировки необходимо ввести ряд первоначальных определений и обозначений.

Во-первых, вместо интервала , общепринятого множества значений функции принадлежности, рассматривается непустое множествос отношением частичного порядкаи операциями, удовлетворяющими свойствам коммутативности, ассоциативности и дистрибутивности, а также содержащие нулевой (0) и единичный (1) элементы.

Во-вторых, рассматриваются инструкции следующего вида:

Start: go to	(инструкция начала);
: do , go to	(инструкция операции);
: if then go to ()	(инструкция условия);
: halt	(инструкция окончания)

где — множество символов меток инструкций,— символ оператора или функции,— символ предикатов или условий.

Введение понятия инструкции позволяет определить понятие программы. Под программой понимается конечное множество инструкций , содержащее единственную инструкцию начала. Никакие инструкции изне имеют одинаковых меток.

В-третьих, определяется понятие -машины. -машина есть функция, определенная на множестве символов, для которых существуют множество входов, множество состояний памятии множество выходов, а также выполнены следующие условия:

1. (функция входов);

2. (функция операции);

3. , (функция условий);

4. (функция выхода).

Символы иобозначают вход и выход. Наконец, в-четвертых, программавместе с-машиной, котораядопускает (т.е. машина определена на всех операцияхи условиях, содержащихся в инструкциях операции и условия программы), называетсянечеткой программой. Следовательно, последовательностью инструкций, составляющих нечеткую программу, определяется нечеткий алгоритм.

Конкретные типы алгоритмов могут быть получены посредством выбора множеств , функций (входов, действий, условий, выходов), операций, отношения.

Рассмотрим некоторые случаи выбора множеств, функций, операций, отношений. Пусть — непустые множества, тогда функциюизвбудем называть-функциейизв;есть степень, с которой значение функции в точкеесть.

-функция является вероятностной, если для любого существуети.

-функция является детерминированной, если для любого существуети для любого.

Если множество с определенными на нем операциями и отношениями записать в виде четверки, то:

• — определяет максиминную машину;

• — определяет взвешенную машину;

• — минимаксную машину;

• — максимально взвешенную машину;

• — недетерминированную машину.

Взвешенная машина является вероятностной, если функции входа, действий, условий, выхода являются вероятностными. Любая же машина, в которой перечисленные функции являются детерминированными, называется детерминированной.

Рассмотрим программу , которую допускает-машина. Для каждой пары метоки пары состоянийбудем писать, если в программелибо имеется инструкция вида, гдеесть степень, с которой осуществляется переход из состоянияв состояние, либо имеется инструкция вида, гдедля некоторогоиесть степень, с которой осуществляется переход на метку.

Выполнением программы на-машине, допускающей, называется конечная последовательность. Выполнение возможно тогда и только тогда, если, где,,.

Таким образом, возможное выполнение определяет последовательность инструкций программы , которая может быть реализована на-машине. Таких последовательностей может быть несколько.

Приведем другую формулировку нечеткой программы, которая является частным случаем данного выше определения нечеткой программы, так как здесь рассматриваются машины с конечным множеством состояний, которые моделируются конечными автоматами.

Для определения нечеткого алгоритма первоначально вводится понятие обобщенной машины, на основе которого формулируется понятие обобщенной нечеткой машины, которое позволяет формализовать понятие нечеткого алгоритма.

Обобщенная машина есть шестерка , гдеи— конечные непустые множества машинных инструкций и внутренних состояний соответственно,— непустое множество с отношением частичного порядкаи операциями, удовлетворяющими свойствам коммутативности, ассоциативности и дистрибутивности, а также содержащие нулевой и единичный элементы;—-функция переходов из состояния в состояние;;и— начальное состояние и множество финальных состояний.

Для цепочки инструкций (— множество всевозможных цепочек инструкций) переходов из состояниявопределяется степенью.

Если — пустая цепочка инструкций, то задается расширенная-функцияследующим образом:

Обобщенная нечеткая машина определяется парой , где — обобщенная машина, — конечное множество нечетких инструкций и каждая нечеткая инструкция изесть -функция из в.

Пусть задана некоторая обобщенная нечеткая машина . Выполнение последовательностина обобщенной машинеесть последовательность

Весом, соответствующим выполнению, является элемент

где

Выполнение возможно тогда и только тогда, если . Еслиипринимают значения из различных множестви, то вес, соответствующий выполнению, будет определяться парой. В этом случае говорят, что программавыполнима с весом, если.

Пример. Пусть имеется последовательность инструкций для водителя автомобиля и карта местности. Водителю предлагается найти место назначения, используя карту и последовательность нечетких инструкций, описывающих маршрут. Для простоты изложения предположим, что все точки на плоскости имеют только целочисленные координаты. Типичные инструкции для водителя: "двигаться прямо около метров", "повернуть налево", "повернуть направо", "двигаться прямо до тех пор, пока не увидишь ...".

Сконструируем соответствующую -машину.-машина имеет множество состояний памятив виде упорядоченных троек, где— точка на плоскости, соответствующая местонахождению автомобиля,— единичный вектор направления движения автомобиля. Множество входови множество выходовсостоят из упорядоченных пар;— функция входов, соответствует тождественной функции;— функция выходов, соответствует функции, отображающей каждую тройкув.

Машина не имеет ни одной функции условия. Каждой инструкции, приведенной выше, соответствует функция операции. При этом-я инструкция в последовательности инструкций может быть преобразована в инструкцию операции вида do; go to. Совокупность таких инструкций и инструкций start: go toи: halt, где— длина последовательности, составляет программу. Процесс выполнения программына машинеопределяется последовательностью инструкций и картой местности. Краткости ради приведем только функцию операции для инструкции типа "двигаться прямо околометров":

где — степень (вес), соответствующая расстоянию,|— вес, соответствующий утверждению: "точкаи направлениедостижимы при движении прямо из точкипо направлению".

Примеры функций и, где— параметр:тогда и только тогда, есливектор извпараллелени каждая точка на отрезке линии, проходящей черези, имеющая целые координаты, есть точка на карте. Очевидно, чтозависит только от, азависит только от карты. Другие функции операций могут быть построены аналогично.Нечеткий алгоритм, описывающий движение автомобиля к месту назначения, определяется конкретной последовательностью инструкций приведенного вида, которая реализуется на рассмотренной -машине.

Приведем другие примеры применения нечетких алгоритмов.

• Алгоритмы определения сложного нечеткого понятия через более простые понятия, которые легко описать нечеткими множествами; результатом применения таких алгоритмов к некоторому элементуобласти рассужденийбудет степень принадлежностипонятию(степень, с которой элементможет характеризоваться понятием);

• Алгоритмы порождения, в результате выполнения которых порождается один из элементов нечеткого множества, которое описывает интересующее нас понятие (например, алгоритм порождения образцов почерка, рецептов приготовления пищи, сочинения музыки, предложений в естественном языке);

• Алгоритмы описания отношений между нечеткими переменными, например, в виде последовательности нечетких инструкций типа: "если мало иувеличить слегка, тоувеличится слабо"; такие алгоритмы позволяют приближенно описывать поведение систем, входные и выходные сигналы которых являются нечеткими подмножествами;

• Алгоритмы принятия решения, позволяющие приближенно описывать стратегию или важнейшее правило, например, алгоритм проезда перекрестка, содержащий последовательность действий, которые необходимо выполнить, при этом описания этих действий состоят из нечетких понятий типа: нормальная скорость, несколько секунд, медленно приближаться.

Способы выполнения нечетких алгоритмов

Для реализации поиска какого-либо выполнения нечеткого алгоритма необходимо определить правила выбора машинной инструкции на каждом шаге. Правила выбора машинной инструкции и переходов из состояния в состояние зависят от типа нечеткой машины.

Выбор машинной инструкции:

a. Нечеткий выбор. Машина выбирает машинную инструкцию с наивысшей степенью на каждом шагедля любой инструкции.

b. Вероятностный выбор. Машина на каждом шаге нечеткой инструкции выбирает инструкциюс вероятностью, пропорциональной нечеткой степени

c. Недетерминированный выбор. Машинная инструкция выбирается недетерминированным образом.

Определение перехода из состояния в состояние:

a. Нечеткий переход. Машина переходит из состояния в состояниедля любого состояния.

b. Вероятностный переход. Машина переходит из состояния в состояниес вероятностью

c. В случае детерминированного перехода состояние, пригодное для машины, единственным образом определяется функцией переходов .

Процедура возврата:

a. Вернуться на предыдущую нечеткую инструкцию.

b. Вернуться на нечеткую инструкцию, соответствующую машинной инструкции с наивысшей функцией принадлежности в ряде таких инструкций, просмотренных последовательно до выбранной нечеткой инструкции.

c. Осуществить возврат так же, как описано в пункте (b), но при этом машинная инструкция выбирается со степенью более высокой, чем выбранная перед этим.

Представление нечеткого алгоритма в виде графа

Во многих случаях нечеткий алгоритм удобно представлять в виде ориентированного графа. Каждой дуге ставят в соответствие инструкцию условия или инструкцию операции. Входные, выходные, внутренние переменные в нечетком алгоритме представляются нечеткими множествами. Выполнение алгоритма эквивалентно поиску в графе путей, связывающих помеченные вершины: начальные и конечные. Приведем необходимые для дальнейшего изложения известные определения графа и путей в графе.

Определение. Графом называется тройка, где— множество элементов, называемых вершинами графа;множество элементов, называемых ребрами графа, причем;— функция, ставящая в соответствие каждому ребруупорядоченную или неупорядоченную пару вершин,иназываются концами ребра. Если множествоконечно, то граф называется конечным. Если— упорядоченная пара (т.е.), то реброназывается ориентированным ребром или дугой, исходящей из вершиныи входящей в вершину;называется началом,— концом дуги. Граф, все ребра которого ориентированные, называется ориентированным графом.

Определение. Последовательность вершин и ребер графа называется путемиз вершиныв вершину, еслидля. Вершинаназывается началом, а— концом пути; числоназывается длиной пути.

Определение. Нечеткая программа есть четверка , где— вектор входа,— вектор программы (внутренние переменные),— вектор выхода,— ориентированный граф:

• — нечеткие переменные, определяющие нечеткие множества на ;

• В графе существует точно одна вершина, называемая начальной (стартовой), которая не является конечной вершиной никакой дуги, и существует точно одна вершина, называемая конечной (финальной), которая не является начальной вершиной никакой дуги: любая вершина графа находится на некотором пути из стартовой вершиныв финальную вершину;

• В графе любая дуга, не ведущая в, связана с нечетким отношениеминечеткой инструкцией ; каждая дуга, ведущая в, связана с нечетким отношениеми инструкцией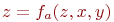, где— нечеткое отношение, и— нечеткая операция типа пересечения, объединения, отрицания нечеткой арифметики, оператор размывания, оператор типа модификаторов и т.д.

Нечеткие алгоритмы обучения

Известно, что обучающиеся системы улучшают функционирование в процессе работы, модифицируя свою структуру или значение параметров. Предложено большое число способов описания и построения обучающихся систем. Все они предполагают решение следующих задач: выбор измерений (свойств, рецепторов); поиск отображения пространства рецепторов в пространство признаков, которые осуществляют вырожденное отображение объектов; поиск критерия отбора признаков. Причем в различных задачах для получения хороших признаков могут понадобиться разные критерии отбора. При обучении необходимо отвлечься от различий внутри класса, сосредоточить внимание на отличии одного класса от другого и на сходстве внутри классов. Необходим достаточный уровень начальной организации обучающейся системы. Для сложной структурной информации необходима многоуровневая обучающаяся система.

Следует выделить следующие группы нечетких алгоритмов обучения: обучающийся нечеткий автомат, обучение на основе условной нечеткой меры, адаптивный нечеткий логический регулятор, обучение при лингвистическом описании предпочтения.

Рекуррентные соотношения в алгоритмах первых двух групп позволяют получать функцию принадлежности исследуемого понятия на множестве заранее известных элементов. В третьей группе нечеткий алгоритм обучения осуществляет модификацию нечетких логических правил для удержания управляемого процесса в допустимых границах. В четвертой группе нечеткий алгоритм обучения осуществляет поиск вырожденного отображения пространства свойств в пространство полезных признаков и модификацию на их основе описания предпочтения.

Обучающийся нечеткий автомат

Рассмотрим автомат с четким входом и зависимым от времени нечетким отношением перехода. Пусть— нечеткое состояние автомата в момент временина конечном множестве состоянийи— оценка значения.Состояние автомата в момент времениопределяется-композицией:

или аналогично ей. Обучение направлено на изменение нечеткой матрицы переходов:

где . Константаопределяет скорость обучения. Начало работы автомата возможно без априорной информацииили 1, а также с априорной информацией. Величиназависит от оценки функционирования автомата. Доказано, что имеет место сходимость матрицы переходов, независимо от того, есть ли априорная информация, т.е.может быть любым значением из интервала.

Пример. На рис. 12.1 изображена модель классификации образов. Роль входа и выхода можно кратко объяснить следующим образом. Во время каждого интервала времени классификатор образов получает новый образец из неизвестной внешней среды. Далееобрабатывается в рецепторе, из которого поступает как в блок "обучаемый", так и в блок "учитель" для оценки. Критерий оценки должен быть выбран так, чтобы его минимизация или максимизация отражала свойства классификации (классов образов). Поэтому, благодаря естественному распределению образов, критерий может быть включен в систему, чтобы служить в качестве учителя для классификатора. Модель обучения формируется следующим образом. Предполагается, что классификатор имеет в распоряжении множество дискриминантных функций нескольких переменных. Система адаптируется к лучшему решению. Лучшее решение выделяет множество дискриминантных функций, которые дают минимум нераспознавания среди множества дискриминантных функций для данного множества образцов.

увеличить изображение Рис. 12.1.

Моделируется поиск глобального экстремума функции следующим образом:

• область определения целевой функции делится на некоторое число подобластей (форма подобластей постоянно меняется) и описывается некоторым множеством точек;

• каждой точке приписывается состояние автомата, причем функция принадлежности в каждом состоянии указывает степень близости к оптимуму;

• выбирается состояние с максимальным значением функции принадлежности (эта точка называется кандидатом);

• формируется новая подобласть из точек, окружающих кандидата (размер подобласти растет, когда значение целевой функции в точке кандидата меньше, чем в других точках подобласти, и уменьшается в противоположном случае);

• когда подобласть пересекается с некоторой другой, или две точки-кандидаты находятся в одной подобласти, то подобласти разделяются, если степень разделения большая, или объединяются, если степень разделения малая;

• точки-кандидаты выбираются на этапе локального поиска в подобласти, затем во всей области среди точек-кандидатов ищется глобальная оптимальная точка;

• глобальный и локальный поиск осуществляется поочередно.

Алгоритм поиска глобального экстремума приведен на рис.12.2.

увеличить изображение Рис. 12.2.

Пусть — множество состояний,— выходной универсум,— функция выхода (функция принадлежности, указывающая степень оптимума в состоянии),— текущее значение целевой функции,— среднее значение.

Используется следующий алгоритм изменения функций перехода и выхода в случае глобального поиска:

если , то попытка успешна и

если , то попытка неудачна и

где ;— гарантируемая сходимость.

В случае локального поиска:

если , то

если , то

Обучение на основе условной нечеткой меры

Пусть — множество причин (входов) и— множество результатов. Если— функция изв интервал,и— нечеткая мера на, то

где .

Задача состоит в оценке (уточнении) причин по нечеткой информации.

Пусть — нечеткая мера на,связана сусловной нечеткой мерой:

Предполагается следующая интерпретация вводимых мер: оценивает степень нечеткости утверждения "один из элементовбыл причиной",,оценивает степень нечеткости утверждения "один из элементовявляется результатом благодаря причине";характеризует степень нечеткости утверждения: "— действительный результат".

Пусть описывает точность информации, тогда по определению.

Метод обучения должен соответствовать обязательному условию: при получении информации нечеткая мераменяется таким образом, чтобывозрастала. Предположим, чтоиудовлетворяют-правилу. Пустьявляется убывающей, тогда

где . При этих условиях существует:

Обучение может быть осуществлено увеличением тех значений () нечеткой меры, которые увеличивают, и уменьшением тех значений() меры, которые не увеличивают. Можно показать, что на величинувлияют только такие, что. Следовательно,нечеткий алгоритм обучения следующий:

Параметр регулирует скорость обучения, т.е. скорость сходимости. Чем меньше, тем сильнее изменяется. В приведенном алгоритме нет необходимости увеличиватьбольше, чем на, так как большое увеличениене влияет на. Приведем некоторые свойства модели обучения.

Свойство 1. Если повторно поступает одна и та же информация, то происходит следующее:

a. новое больше старого() и новоеменьше старого(), следовательно, новая меране меньше старой меры, и новая мера

b. при предположении ,,сходится кисходится к 0 для.

Свойство 2. Если поступает одна и та же информация повторно: для всех, то.

Следовательно, исходится кдля всех.

Свойство 3. Предельное значение не зависит от начального значения тогда, когда на вход повторно поступает одна и та же информация.

Пример. Рассмотрим модель глобального поиска экстремума неизвестной функции с несколькими локальными экстремумами. Для поиска глобального экстремума формируются критерии в виде некоторых функций:

— оценивает число точек, проанализированных на предыдущих шагах;

— оценивает среднее значение функции по результатам предыдущих шагов;

— оценивает число точек, значение функции в которых принадлежит десятке лучших в своей области;

— оценивает максимум по прошлым попыткам;

— оценивает градиент функции.

В описанном случае показывает степень важности подмножеств критериев иоценивает предположение о нахождении экстремума в блокев соответствии с критерием. Например,может зависеть от числа ранее проанализированных точек в блоке. Пусть входная информацияопределяется формулой

где — максимум анализируемой функции, найденный к рассматриваемому моменту в блоке. Очевидно, чтосходится к максимизирующему множеству функции. На каждой итерации осуществляется следующее: проверяется заданное число новых точек; число этих точек выбирается пропорционально; в~каждой точкевычисляется и нормализуется мера); нормализуется; поивычисляется, а затем; посредством правил подкрепления корректируется. Затем выполняется новая итерация, и так до тех пор, пока не сойдется.

Адаптивный нечеткий логический регулятор

В настоящее время наиболее широкое применение при решении практических задач получили нечеткие логические регуляторы, которые позволяют на основании лингвистической информации, полученной от опытного оператора, управлять сложными, плохо формализованными процессами.

увеличить изображение Рис. 12.3.

Структура нечеткого логического регулятора, в котором используются эвристические правила принятия решений, показана на рис. 12.3 Такие регуляторы применяются аналогично традиционным регуляторам с обратной связью. Определение управляющих воздействий состоит из четырех основных этапов:

1. Получение отклика;

2. Преобразование значения отклонения к нечеткому виду, такому, как "большой", "средний";

3. Оценка входного значения по заранее сформулированным правилам принятия решения с помощью композиционного правила вывода;

4. Вычисление детерминированного выхода, необходимого для регулирования процесса.

Рис. 12.4.

Опишем способ уточнения правил управления, используемых в адаптивном нечетком логическом регуляторе (АНЛР). Соответствующая схема регулятора приведена на рис. 12.4 АНЛР состоит из двух частей: нечеткого логического регулятора управляемого процесса (НЛРУП) и нечеткого логического регулятора управления (НЛРУ). На рис. 12.4 используются следующие обозначения:

— управление, генерируемое НЛРУП;

— ошибка (отклонение от устанавливаемого выходного значения процесса );

— желаемое значение выхода управляемого процесса, ;

— модификация управления.

Правила НЛРУП имеют форму: if then ifthen.

Правила НЛРУ имеют форму: if then ifthen.

Здесь ,,,,,— предварительно описанные нечеткие множества. Символиспользуется для модификации стратегии управления следующим образом: в нечетком правиле, которое ухудшает течение процесса, заменяется значение управленияна. Правилов НЛРУП заменяется на правило ifthen ifthen.

Рассмотрим далее два нечетких алгоритма обучения при лингвистическом описании предпочтений: алгоритм формирования нечеткого отношения предпочтений на множестве альтернатив, описываемых наборами лингвистических значений признаков, и алгоритм уточнения лингвистических критериев.

Алгоритм формирования нечеткого отношения предпочтения

Пусть — множество таких альтернатив, что каждоехарактеризуется набором оценок попризнакам:, и пусть— семейство всех непустых конечных подмножеств множества. Для некоторогоизвестно подмножество выбранных альтернатив, т.е. для любыхиимеет место доминирование. Предварительно, при анализе исходного множества альтернатив, сформирован эталонный набор нечетких оценок. Значения функции принадлежности нечеткой оценкиуказывают на степень близости значений-го признака к значениям, определяющим идеальную альтернативу. Используя множество предпочтений

требуется найти обобщенные правила предпочтения на множестве .

Пример. Рассмотрим задачу выбора для рыболовецкого судна рационального района промысла с учетом следующих показателей: — время перехода в район лова,— прогноз вылова,— стоимостная характеристика прогнозируемого объекта лова,— гидрометеоусловия. Показатели, в сущности, играют роль лингвистических переменных.

Лицу, принимающему решение, предложены альтернативы —(см.табл.12.1). Пусть выбрана альтернатива . Для обучения формируются две таблицы:

Таблица 12.1.
	U1	U2	U3	U4		U1	U2	U3	U4
S1	хор.	хор.	хор.	уд.	S1	плох.	хор.	плох.	уд.
S2	оч. хор.	плох.	хор.	уд.	S2	уд.	хор.	хор.	неуд.
S3	оч. хор.	хор.	хор.	неуд.	S3	плох.	хор.	хор.	уд.
S4	уд.	хор.	хор.	уд.	S4	уд.	хор.	норм.	уд.
S5	оч. плох.	хор.	хор.	уд.	S5	уд.	норм.	норм.	уд.
S6	хор.	норм.	плох.	уд.	S6

Для каждой пары наборов вычисляются оценки сравнения-го элемента первого набора с-м элементом второго набора:

где определяет конкретный оператор, например, нечеткую меру сходства.

В результате получаются две таблицы наборов нечетких оценок поэлементного сравнения. На основе полученных таблиц, используя логические операторы и логические функции двух переменных, выделяются полезные признаки и минимальный базис. Содержательное значение утверждения, соответствующего минимальному базису, следующее:

где — лингвистическое значение-го показателя,— логический признак. Физический смысл приведенного утверждения: районпредпочтительнее района, если утверждение [(время перехода до"меньше", чем до), и (прогноз вылова в"больше", чем в), и (погодные условия в"лучше", чем в)] более истинно, чем обратное утверждение [(время перехода до"больше", чем до), и (прогноз вылова в"меньше", чем в), и (погодные условия в"хуже", чем в)].

Далее предположим, что среди неизвестных ситуаций -(табл. 12.1) необходимо выбрать лучшую альтернативу, используя минимальный базис. В табл. 12.2 изображена матрица предпочтений , элементы которой вычислялись посредством гарантированной оценки

Таблица 12.2.
	S7	S8	S9	S10	S11
S7		0,88 0,38	1 0,38	0,88 0,38	0,88 0,38
S8	0,75 1		0,75 1	0,75 1	0,75 1
S9	1 0,38	0,88 0,38		0,88 0,38	0,88 0,38
S10	1 0,38	1 0,38	1 0,38		1 0,38
S11	0,88 0,38	0,88 0,38	0,88 0,38	0,88 0,38

где — значение-го признака на паре альтернатив— значение-го признака на парах альтернатив-го класса (). Каждый элемент матрицы содержит два значения. Левое значение указывает степень, с которойдоминирует над. Правое значение указывает степень, с которойдоминирует над. Для построения нечеткого графа предпочтений альтернатив (рис.12.5) используется следующее правило определения отношения доминирования :

где

Рис. 12.5.

Согласно рис. 12.5, является недоминируемой альтернативой, т.е. не существует альтернативы, которая с ненулевой степенью доминирует над.

Алгоритм уточнения лингвистических критериев

Глобальные представления ЛПР о выборе альтернатив формулируются в виде глобального критерия, и решение многокритериальной задачи сводится к построению композиции , где

, — множества значений признаков, локальных и глобального критериев, соответственно.иформируются на основе высказываний типа: "если значения признаков, характеризующие альтернативу, оцениваются термами, то альтернатива удовлетворяет-му критерию с оценкой".

и описываются наборами

Степень удовлетворения глобальному критерию для альтернативы вычисляется следующим образом:

В процессе обучения уточняются оценки глобального и локальных критериев на основе сравнения выбранных ЛПР альтернатив из множества предъявленных.заменяется некоторым, подтверждающим соответствующий выбор:

Обучение осуществляется в два этапа: формирование обобщенных описаний предпочтения ЛПР; модификация M при несовпадении предпочтений ЛПР с порядком оценок . На втором этапе выполняется следующее: генерация допустимых наборов оценок показателей; определение отношения предпочтения на парах сгенерированных альтернатив; выделение изнаборов, не подлежащих корректировке; корректировка оценок по критериям.