54

Ее изображением будет L(f(t))= ∞∫ f (t)e−pt dt =Фо(p). Сам оригинал в этом

0

случае можно рассматривать в виде f(t)(1(t)-1(t-τ )).

Так, например, для единичного импульса получаем 1(t)-1(t-τ ). А изображением единичного импульса по теореме сдвига в оригинале будет F(p)=

Изображение периодической функции. Для периодической f(t) с

периодом Т можно говорить, что сдвиг τ =Т и на каждом периоде [nT;(n+1)T] величина f(t) получается сдвигом импульса на соответствующую величину nT. Таким образом, сдвинув импульс на nT , на интервале [nT;(n+1)T] получаем изображение e−npT Фо ( p) , где Фо(p) – изображение импульса на первом периоде.

Т.к. каждая ступенька действует только на своем интервале, то по свойству линейности прямого преобразования Лапласа все ступеньки следует

15.4. Обратное преобразование Лапласа.

разрыва f(t)=0,5(f(a+0)+f(a-0)).

Интеграл в определении называют интегралом Бромвича (РиманаМеллина).

Если же нам неизвестно, является ли F(p) изображением какого-то оригинала, то следует проверить выполнение достаточного условия по теореме:

Если F(p) аналитична в полуплоскости Rep=s>so ; F(p)Æ0 при p → ∞; и

интеграл ∞∫ F( p) dp сходится, то F(p) изображение и оригинал определяется

−∞

интегралом Бромвича.

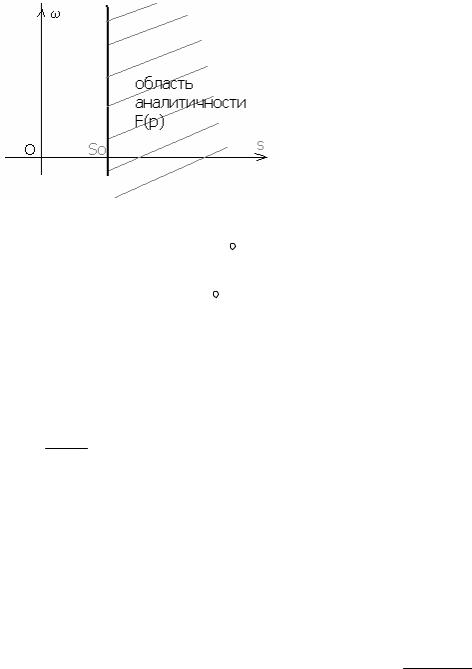
Отметим, что интеграл Бромвича малопригоден на практике, т.к. нужно знать поведение F(p) при p ->∞. Подойдем к решению задачи с другой стороны.

1 s+i∞

Интеграл ∫F ( p)e pt dt берется по прямой Rep=s , причем модуль р – любой, а

2π i s−i∞

аргумент р меняется от -∞до ∞. При этом путь интегрирования снизу вверх

54

55

по прямой s=so , справа от которой область аналитичности без особых точек, т.к. все они расположены (если они есть) слева от прямой s=so. Это означает, что мы имеем право рассматривать эту прямую как окружность – контур, который охватывает все особые точки функции F(p).

Рис 15.5. К обратному преобразованию.

где вычеты взяты по всем особым точкам слева от вертикали s=so. Получаем теорему : если F(p) аналитична на комплексной плоскости за исключением конечного числа особых точек, и lim maxF(p) =0 при pÆ∞, тогда при tÆ0 верно равенство (15.2 ).

Другим приемом восстановления оригинала по изображению, если

F(p)= Qn ( p) является разложение правильной дроби на простейшие методом

Rm( p)

неопределенных коэффициентов и последующим применением таблицы соответствия оригиналÆизображение. Для случая простейших дробей первых трех типов достаточно таблицы. А если дробь имеет тип 4-й, то применяют теорему о свертке.

Еще одним приемом восстановления оригинала по изображению можно считать разложение F(p) в ряд Лорана, если имеется существенно особая точка. И далее опять таблица. При этом оригинал будет представлен в виде степенного ряда. В некоторых случаях этого вполне достаточно.

4 − p − p2

Пример 15.5. Найдите оригинал , если F(p)= p3 − p2 .

Решение. В самом деле , F(p) оригинал, хотя бы потому что при pÆ0 F(p)Æ0. Эта функция аналитична везде за исключением точек z1=0 – полюс порядка 2 и z2=1 – простой полюс. Найдем оригинал по основной теореме о вычетах с

55

56

Решение. В самом деле , F(p) оригинал, хотя бы потому что при pÆ0

π +2kπ

F(p)Æ0. Эта функция аналитична везде за исключением точек z1,4= ei 4 и z2=0

– простые полюсы. Но восстанавливать f(t) будем иначе , Разложим F(p) в ряд

15.6. Решение задачи Коши операционным методом.

Ограничимся наиболее распространенным линейным дифференциальным уравнение 2-го порядка со специальной правой частью.

Пусть требуется решить задачу Коши

y(x) –оригинал с изображением Y(p). Далее проcто Y.Пусть изображение для f(x) имеет вид F=F(p). Тогда по свойству линейности прямого преобразования Лапласа получаем p2Y-p yo - y’o + a1 (pY- yo )+ a2Y= F(p).

восстановление оригинала по полученному изображению.

Пример 15.7. Решите задачу Коши y’’+y’-2y=e-x, при y(0)=0 ,y’(0)=1.

Решение. Т.к. уравнение линейное и правая часть оригинал, то решение задачи тоже оригинал. Пусть оригиналом решения задачи будет Y(p). Тогда по теореме дифференцирования оригинала получаем изображение для y’ в виде pY-0; а изображением 2-1 производной будет p2Y-p0-1. Т.к. изображением для правой части будет 1/(p+1), то в пространстве изображений задача принимает вид

линейности получаем решение задачи y=0,5(et – e-t).

56

57

16. Элементы математической физики

16.1. Основные понятия.

Предмет математической физики. Известны условия “в малом”, в которых находится объект (протекает процесс). Найти интегральный закон (поле величины, процесса) .

Основными уравнениями математической физики являются линейные дифференциальные уравнения в частных производных (с частными производными) . Ограничимся двумерными задачами.

a11(x;y)Uxx+2a12(x;y)Uxy+ a22(x;y)Uyy+F(x;y;U;Ux;Uy)=0 (18.1)

В (18.1) : aij- коэффициенты; Uxy …-частные производные.

Если сравнить ДУ обыкновенные и ДУ в частных производных, то сразу

видна большая сложность задач матфизики. Даже решение уравнения д2U =0

дxдy

приводит сразу к появлению двух произвольных функций, что существенно отличается от интегрирования обыкновенного ДУ.

Вданном курсе будут рассматриваться только уравнения вида (18.1).

16.2.Классификация уравнений матфизики.

(a12)2 не меняет знака и может служить классификатором уравнений матфизики. Если >0 – уравнение называют эллиптическим; если <0 – уравнение называют гиперболическим; если =0 – уравнение называют параболическим.

Вставка доказательства по Арсенину.

16.3. Вывод основных уравнений.

Назовем струной упругую нерастяжимую нить, не сопротивляющуюся изгибу, но оказывающую сопротивление растяжению.

Отсутствие сопротивлению изгиба позволяет упростить расчеты, т.к. в этом случае напряжения в струне всегда будет направлено вдоль ее профиля (по касательной).

Рассмотрим малые движения струны, выведенной из положения равновесия. Рис18.1.

57

58

Рис18.1. К выводу уравнения струны

Выделим элементарный участок струны dS . Тогда dS2=dx2+dU2 , где dU

dU 2

– отклонение струны от положения равновесия. Отсюда dS=dx 1+ dx2 =dx , что

и указывает на нерастяжимость струны.

Запишем для участка dS закон Ньютона в проекциях на ось U. Имеем ma=F, но dm= ρ dx или ma= ρ Uttdx. Но F=T2+T1 . А т.к. струна гибкая, то

получаем Utt-a2(Uxx+ Uуу)=0. Для акустических колебаний (колебаний среды, объемного объекта) получаем Utt-a2(Uxx+ Uуу+ Uzz)=0. Во всех случаях – это собственные (правая часть равна нулю, свободные) колебания. Иногда эти уравнения называют волновыми. Класс их определяется одномерным уравнением.

Если колебательный процесс стационарен (стоячая волна), то уравнение

принимает вид Uxx+ Uуу+ Uzz=0 и для плоского поля U такой Uxx+ Uуу=0 – уравнение Лапласа (уравнение установления потенциала).

Решим еще одну задачу. Пусть имеется объем V, ограниченный поверхностью S. Пусть этот объем нагрет и остывает, отдавая тепло через свой границы (поверхность S). Единственной характеристикой процесса естественно считать температуру в каждой точке в произвольный момент времени T(x;y;z;t). В этом случае количество тепла в этом объеме можно подсчитать, если указать плотность тепловой энергии q= ρ CvT, где Cv - удельная теплоемкость при

V=const. В таком случае в объеме будет ∫∫∫ ρ CvTdv тепла. Скорость

V

изменения тепла (убыль) –это производная по времени от этого интеграла. Т.е.

58

S

указывает на убыль тепла) в направлении внешней нормали к поверхности (см.

Окончательно получаем Tt- k (Txx+Tyy+Tzz) – уравнение теплопроводности. В

Cv

стационарном случае получаем Txx+Tyy+Tzz=0 – тоже уравнение Лапласа установленного (стабилизированного) распространения тепла. Простым примером такого процесса служит нагревание металлической плиты газовой горелкой. По истечении некоторого времени температура в точках плиты стабилизируется.

16.4. Основные задачи. О корректности задач.

Каждое из полученных в 18.3 уравнений имеет много решений, т.к. придется неоднократно интегрировать по разным переменным. И потому общее решение представляет собой абсолютно нереальное понятие. Ведь всякий процесс протекает в заданных условиях вполне определенным образом. В матфизике никогда не ищут общего решения. Поэтому для определенности процесса уравнения матфизики дополняют некоторыми условиями. Если задача стационарная, то это будут граничные условия. Если же нестационарная, то помимо граничных условий следует задат и начальные условия. Так, например, при решении задачи о колебаниях струны следует указать начальную ее форму (начальные условия) и поведение струны на ее концах (граничные).

Естественно, что задание дополнительных условий производится на основании некоторых экспериментальных данных, которые по разным причинам содержат погрешности. Эти погрешности влияют на окончательное решение задачи.

Определение. Если небольшим изменениям начальных и/или граничных условий соответствуют небольшие изменения в решении задачи, то говорят , что задача поставлена корректно.

Мы будем рассматривать только такие задачи.

59

60

16.5. Метод сеток решения задачи Дирихле для уравнения Лапласа

Эту задачу называют задачей Дирихле для уравнения Лапласа. На ней рассмотрим один из методов решения задач матфизики – метод конечных разностей (метод сеток).

Весь процесс решения состоит из нескольких шагов. На первом шаге выполняют аппроксимацию области некоторой сеточной областью. На втором

– аппроксимацию уравнения Лапласа во всех внутренних точках соответствующими конечно-разностными отношениями. И на третьем производят решение новой задачи (аналога исходной) и интерпретацию результатов.

Пусть нам требуется решить задачу (16.2), (16.3). Руководствуемся

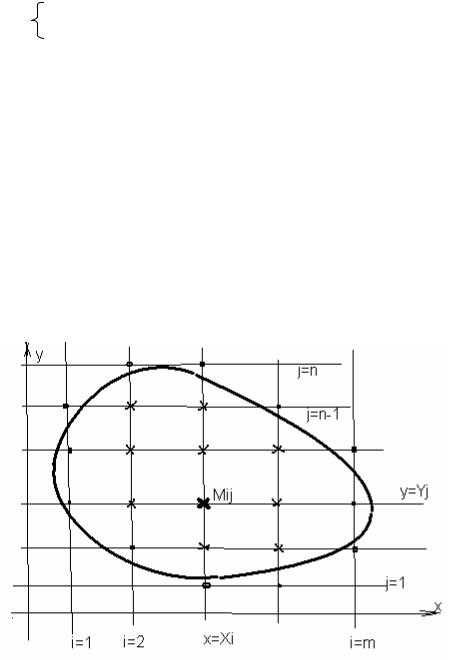
Рис 16.2. Подведем к области D декартову систему координат. Затем проведем две серии прямых x=xi ,i=1,2,…,m, y=yj , j-1,2,…,n. Расстояние между прямыми в серии можно брать произвольно, но лучше постоянным. Тогда пишем так xi+1- xi=hx, yj+1- yj=hy.

Рис 16.2. К методу сеток

Точки пересечения прямых называют узлами и обозначают Mij (xi , yj) по номерам пересекающихся прямых . Затем узлы классифицируют на : граничные

– расстояние от которых до фактической точки пересечения границы с сеточной прямой меньше полшага в направлении одной из координатных осей(отмечены точками) и внутренние , 4 соседних узла которых либо граничные, либо внутренние (отмечены крестом). Соединим граничные узлы отрезками сеточных прямых. В этом случае D будет заменена (аппроксимирована) приближенно сеточной областью Dh.

В каждом граничном узле вычислим приближенно узловое значение по (16.3) . В каждом внутреннем узле для вторых частных производных запишем

60