
- •Введение
- •12. Поверхностные интегралы.
- •12.2. Поверхностный интеграл 2-го рода.
- •13. Элементы теории поля
- •13.1. Некоторые понятия теории поля
- •13.2. Формула Грина.
- •13.3. Формула Остроградского-Гаусса.
- •13.4. Формула Стокса.
- •13.5. Оператор Гамильтона.
- •13.6. Специальные поля.
- •14.2.Основные действия над К.Ч.
- •14.5.Функции комплексного переменного.
- •14.8. Интегрирование ФКП.
- •14.9. Ряды с комплексными членами.
- •14.11.Вычеты и их применение.
- •15. Операционное исчисление.
- •15.3. Основные теоремы.
- •15.4. Обратное преобразование Лапласа.
- •16. Элементы математической физики
- •16.1. Основные понятия.
- •16.2. Классификация уравнений матфизики.
- •16.3. Вывод основных уравнений.
- •16.6. Метод характеристик.
- •16.6. Метод разделения переменных.
- •14.Теория функций комплексного переменного.
40
Отметим, что формулы 14.2 и 14.3 верны и для многосвязной области D. В заключение сформулируем без доказательства теорему Морера (обратная для теоремы Коши) : если f(z) непрерывна в односвязной D и
 ∫f(z)dz = 0, где L принадлежит D, то f(z) аналитична.
∫f(z)dz = 0, где L принадлежит D, то f(z) аналитична.
L
14.9. Ряды с комплексными членами.
Сначала |
рассмотрим |
числовые |
комплексные |
ряды |
вида |
|
∞ |
∞ |
|
|
|
|
|
∑zn = ∑(xn + iyn ) . |
|
|
(14.4) |
|
||
n=1 |
n=1 |
|
|
|
|
|
∞
Теорема. Для сходимости ряда ∑zn необходимо и достаточно, чтобы
n=1
сходились ряды , составленные из действительных и мнимых частей членов исходного ряда.
∞
Доказательство. Необходимость. Пусть ряд ∑zn сходится. Тогда мы
n=1
имеем право переставлять его слагаемые по своему усмотрению без нарушения
∞ |
∞ |
∞ |
характера сходимости.. Получаем ∑zn = ∑xn +i |
∑yn . Т.к. слева ряд сходится |
|
n=1 |
n=1 |
n=1 |
и потому имеет некоторую сумму S=Sx+iSy, то сходятся и ряды справа, т.к. должно быть выполнено равенство комплексных чисел.
|
|
∞ |
Достаточность. |
Пусть после составления рядов |
∑xn и |
|
|
n=1 |
∞ |
∞ |
∞ |
∑yn обнаружено, что они оба сходятся. Тогда их комбинация ∑xn +i |
∑yn |
|
n=1 |
n=1 |
n=1 |
тоже сходящийся ряд. Перегруппируем слагаемые в этих рядах и получим ряд
∞
∑zn тоже сходящийся.
n=1
При исследовании на сходимость числового комплексного ряда не запрещено применять известные признаки сходимости (Даламбера, Коши и др.) однако следует помнить, что указанные признаки справедливы только для знакоположительных рядов. Поэтому предварительно следует составить ряд из модулей членов комплексного числового ряда.
Теперь рассмотрим степенные ряды в комплексной плоскости. Это ряды
∞
вида ∑a n (z − zo ) n . Для такого ряда известна теорема Абеля. Область
n=0
сходимости такого ряда - внутренность круга с центром в zo и некоторым радиусом, который можно вычислить по известным формулам. Не запрещено строить круг сходимости и руководствуясь признаками Коши или Даламбера, предварительно зафиксировав z и построив ряд из модулей членов полученного числового ряда.
40
41
О разложении f(z) в степенной ряд по степеням (z- zo) сначала скажем для функции, аналитической в zo. Это будет обычный ряд Тейлора с коэффициентами Тейлора. это можно установить из следующих соображений.
Преобразуем выражение |
1 |
= |
1 |
|
|
|
|
1 |
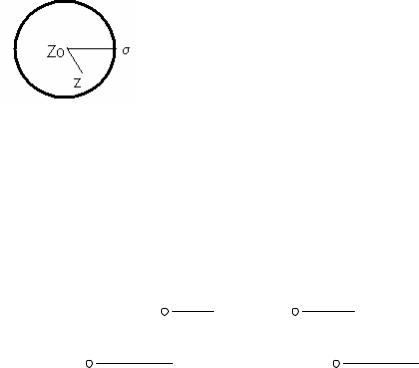
. Рассмотрим рисунок |
|
σ − z |
σ − z |
o 1 |
− |
z − zo |
||||||
|
|
|
||||||||
|
|
|
|
σ − zo |
|
|||||
|
|
|
|
|
|
|
|
|
||
взаимного расположения точек z, zo, и σ на комплексной плоскости. Т.к.. zo- центр круга, σ - точка на контуре, z -произвольная точка внутри контура, то
сразу видно, что |z- zo |<| |
σ- zo |, а потому |
|
z − zo |
|
|
<1 и последнюю дробь можно |
|||
|
|
||||||||
|
|
||||||||
|
σ − zo |
|
|||||||
|
|
||||||||
|
|
|
|
|
|||||
разложить в степенной |
ряд по степеням |
z − zo |
как сумму бесконечно |
||||||
|
|||||||||
|
|
|
|
σ − zo |
|||||
убывающей прогрессии.
Получаем |
|
|
|
|
|
1 |
= |
1 |
|
|
|
|
|
1 |
|
= |
1 |
|
|
|
(1+ |
|
z − zo |
+ |
1 |
|
( |
|
z − zo |
) |
2 |
+ |
|||||||||||
|
|
σ − z |
σ − z |
|
|
|
|
|
|
|
|
σ − z |
|
|
|
|
σ − z |
|
2! |
σ − z |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
o 1 − |
z − zo |
|
o |
|
|
|
|
|
o |
|
|
o |
|
|
|
|||||||||||||||||||||
|
1 |
|
z − zo |
|
|
|
|
|
|
|
|
σ − zo |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
+ |
( |
|
|
) |
3 |
+ ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
σ − zo |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (σ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Если полученное равенство умножить на |
|
и затем проинтегрировать |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
2πi |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
f (σ) |
|
|
|
|
1 |
|
|
|
f (σ) |
|
|
|
|
|
|
|
|
|
|
|
||||
по контуру L , то получим |
|
|
|
∫L σ − zdσ= |
|
|
|
∫L σ − zo dσ + |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
2πi |
2πi |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
+ |
|
1 |
|
|
(z-zo) ∫ |
|
|
|
f (σ) |
2 dσ+ |
|
1 |
|
|
(z-zo)2 |
∫ |
|
f (σ) |
|
|
3 dσ+... |
|
Если |
|||||||||||||||||
|
|
|
2πi |
|
|
|
|
|
|
|
|
|
2πi |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
L (σ − zo ) |
|
|
|
|
|
|
|
|
|
L (σ − zo ) |
|
|
|
|
|
|||||||||||||||||||||
внимательно присмотреться к полученным справа слагаемым, то с учетом множителей видно, что коэффициентами при степенях (z- zo) записаны интегральные представления для производной аналитической в zo функции f(z). Иначе говоря, справа записан ряд Тейлора для функции f(z). Это весьма удобно для записи аналитической функции, т.к. сразу выясняется круг сходимости этого ряда (область соответствия между суммой ряда и представленной функцией). А именно, |z-zo|<R, где - R расстояние от zo до ближайшей особой точки.
Если же zo –особая, то весь вышеприведенный алгоритм не работает, т.к. производную вычислить таком образом в особой точке невозможно.
∞
Рассмотрим еще один вид степенного ряда ∑сn (z − zo )n . Этот ряд принято
n=−∞
41

42
называть рядом Лорана. Легко видет, что ряд можно представить в виде двух
−1 |
∞ |
сумм ∑сn (z − zo )n |
и ∑сn (z − zo )n . Первый из этих рядов называют главной |
n=−∞ |
n=0 |
частью ряда Лорана, а второй – правильной частью. Легко видеть, что правильная часть – это ряд, который сходится в некотором круге с центром в точке zo, а главная часть – это ряд, который сходится вне (снаружи) круга с некоторым радиусом и тем же центром zo. Поэтому ряд Лорана сходится в кольце.
|
Пример |
|
14.9. |
|
Исследовать |
|
|
сходимость |
ряда |
|||||||
…+ |
1 |
+ |
1 |
+ |
1 |
+1+ |
z −1 |
+ |
(z −1) |
2 |
+ |
(z −1) |
3 |
+… |
|
|
23 (z −1)3 |
22 (z −1)2 |
2(z −1) |
5 |
|
52 |
|
53 |
|
|
|||||||
Решение. Сразу видно, что данный ряд – ряд Лорана. Выписав отдельно правильную его часть, зафиксируем z, составим ряд из модулей членов правильной части и применим к ряду из модулей признак Коши . Получим
|
n |
(z −1)n |
z −1 |
|
z −1 |
|
|
|
|
|
|||||
lim |
5n |
= 5 |
Для сходимости требуется , чтобы |
<1. Откуда |
|||
|
|||||||
|
5 |
||||||
n −∞ |
|
|
|
|
|
||
|
|
|
|
|
|
получаем z −1 < 5 . Т.е. правильная часть сходится внутри круга с центром в z=1 и радиусом 5. Проделаем аналогичное для главной части и получим
lim |
1 |
= |
1 |
2n (z −1)n |
2(z −1) |
||
|
n |
|
|
n −∞
. Откуда получаем область сходимости главной
части z −1 > 0,5 - это – внешность круга с тем же центром и радиусом 0,5. Наложением областей получаем кольцо сходимости для ряда Лорана.
Теперь приступаем к выяснению возможности разложения f(z) в ряд по степеням (z- zo) ,если zo не является правильной точкой(т.е. особая точка). Рассуждаем так. Пусть f(z) аналитична везде в D кроме zo . В этом случае f(z) будет аналитична где-то вне этой точки, т.е. в некотором кольце, содержащем эту точку. Ограничим zo двумя контурами так, чтобы сама особая точка оказалась внутри малого круга – в центре кольца. Тогда в самих точках кольца будут справедливы известные формулы Коши (14.2). Значит f(z) может быть
представлена так f(z)= |
1 |
∫ f (σ) dσгде L – некоторый контур, окружающий |
|
||
|
2πi L σ − z |
|
точку . Заменим L сложным контуром, состоящим из двух окружностей кольца и разреза с двумя берегами, соединяющего эти окружности. По этому сложному контуру интеграл, представляющий f(z) может быть представлен так
f(z)= |
1 |
( ∫ f (σ)dσ - |
∫ |
f (σ)dσ ) |
(14.5) |
|
2πi |
||||||
|
l1 σ − z |
l21 |
σ − z |
|
Из этой суммы выпали два интеграла по разным берегам разреза, т.к. в сумме они дают нуль. Теперь поступаем так. Пусть σ принадлежит контуру l1. Преобразуем выражение
42

43
1 |
= |
1 |
|
|
|
|
1 |
= |
1 |
|
(1+ |
z − zo |
+ ( |
z − zo |
) |
2 |
+ ( |
z − zo |
) |
3 |
+… |
|||
σ − z |
σ − z |
o 1 |
− |
z − zo |
σ − z |
o |
σ − z |
o |
σ − z |
o |
|
σ − z |
o |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
σ − zo |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
причем полученный ряд сходится внутри кон тура l1.
Рис 14.10. К разложению в ряд Лорана.
Умножим его почленно на f2(πσi) и проинтегрируем по l1. Тогда слева получим
значение f(z) по формуле Коши, а справа ряд с коэффициентами, представляющими соответствующие производные для f(z) в интегральной форме, т.к. zo – особая.
∞ |
|
1 |
∫ |
f (σ) n+1 dσ . |
|
Ряд ∑сn (z − zo )n в котором |
коэффициенты имеют вид Сn= |
||||
2πi |
|||||
n=−∞ |
|
L |
(σ − zo ) |
Следует иметь в виду, что это уже не частное от деления производной на факториал как было раньше, т.к. f(z) неаналитична в zo.
Теперь проделаем аналогичное для второго слагаемого в скобке в (14.5).
|
1 |
= |
−1 |
|
|
|
1 |
|
= |
|
−1 |
(1+ σ − zo |
+ (σ − zo )2 |
+ ( |
σ − zo )3 |
+ … |
(14.6) |
|||||||||
|
σ − z |
z − zo |
|
|
σ − zo |
|
z |
− zo |
||||||||||||||||||
|
|
1 |
− |
|
|
z − zo |
|
z − zo |
|
|
z − zo |
|
|
|
||||||||||||
|
|
|
|
|
z − zo |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следует обратить внимание на тот факт, что интегрирование идет по |
||||||||||||||||||||||||
контуру l2, |
для которого |
верно неравенство |
|
σ − zo |
|
< |
|
z − zo |
|
в отличие от |
||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
неравенства, |
|
справедливого ранее |
|
|
|
|
. |
Но |
в обоих случаях |
|||||||||||||||||
|
|
σ − zo |
> |
z − zo |
||||||||||||||||||||||
используется для представления сумма геометрической убывающей прогрессии. По этой же причине преобразование дроби выполнено по другому.
После умножения обеих частей равенства (14.6) на f2(πσi) и последующего интегрирования по контуру l2 получаем представление f(z) для z вне контура l2.
∞ |
1 |
∫ f (σ)(σ − zo )n−1 dσ . |
|
И справа опять ряд, но уже вида ∑с−n (z − zo )−n , где С-n= |
|||
|
|||
n=−∞ |
2πi l2 |
||
Если учесть знак общий для всех слагаемых ряда справа, то следует полученные представления просуммировать в формуле (14.5). В результате слева будет получен ряд Лорана как представление для f(z) в окрестности особой точки.
43

44
На основании изложенного получаем алгоритм разложения функции f(z) в ряд Лорана в окрестности точки zo.
1-й шаг – выясни, будет ли центр будущего кольца сходимости точкой правильной или особой; если правильная , то разлагай по известной схеме в ряд Тейлора; в противном случае переходи к шагу 2;
2-й шаг – вычисляй коэффициенты Сn по указанным выше формулам и записывай полученный ряд или переходи к шагу 3;
3-й шаг – возьми подходящий табличный ряд Тейлора и преобразуй его учитывая , что zo – особая .
Пример 14.10. Разложите в ряд Лорана по степеням (z+i) функцию w=1/sinz.
Решение. zo =-i – правильная точка для w. Поэтому в отсутствии подходящего табличного ряда Тейлора вычисляем несколько производных от w
и записываем ряд Тейлора. Имеем w(i)=1/Sini; w’= |
coz |
|
z=−i = |
cosi |
. Составляем |
|
|||||
sin 2 z |
|
sin 2 i |
|||
|
ряд. Он имеет вид w= sin−1i + sincoi2 i (z+i)+ sincos2ii (z+i)2 +…. Область сходимости ряда
– круг с центром в zo и радиусом, равным расстоянию от до ближайшей особой точки функции w – точки 0. Т.е. область сходимости z −i <1.
14.10.Классификация нулей и особых точек.
Определение. Нулем аналитической f(z) , не равной нулю тождественно, называют такое а, при котором f(a)=0.
Определение. Если f`(a)= f``(a)= f```(a)=… =f(n-1) (a) =0, но f(n-1) (a) ≠0, то а называют нулем кратности n для f(z).
Определение. Особая точка zo называется изолированной особой для функции f(z), если существует такое r, что в окрестности z − zo < r нет других
особых точек.
Будем рассматривать и классифицировать только такие особые точки. В этом случае функция аналитична в вырожденном кольце, окружающем эту точку и эту функцию можно разлагать в ряд Лорана по степеням z-zo .
Определение. zo называют устранимая особая точка f(z) , если
lim f (z) = A ≠ f (zo)
z → zo
Теорема. Для того , чтобы zo была устранимой особой точкой для f(z), необходимо и достаточно, чтобы лорановское разложение не имело главной части (т.е. было рядом Тейлора).
Определение. zo называют полюсом функции f(z) , если |
lim f (z) = ∞ |
. |
z → zo |
Теорема. Для того , чтобы zo была полюсом для f(z), необходимо и достаточно, чтобы лорановское разложение имело в главной части конечное число слагаемых.
44
