
Теорема об изм_ КЭ
.pdfФедеральное агентство по образованию
_______________________________________________________________
Государственное образовательное учреждение высшего профессионального образования
Санкт-Петербургский Государственный технологический институт ( Технический университет )
________________________________________________________________
Кафедра теоретической механики
Ю.А. ИВАНОВ, Л.В. КОЛПАКОВА, Л.И. ПОГРЕБНАЯ
Теорема об изменении кинетической энергии
Методические указания
Санкт-Петербург
2009
УДК 531
Иванов Ю.А. Теорема об изменении кинетической энергии: методические указания ./ Иванов Ю.А., Колпакова Л.В., Погребная Л.И..- СПб., СПбГТИ(ТУ), 2009.- 23 с.
В методическом указании содержится систематизированный материал по решению задач курса теоретической механики. Сделан акцент на применение основных законов динамики применительно к особенностям специальностей технологов. Методические указания предназначены для студентов первого и второго курса всех химико-технологических факультетов. Предлагаемое методическое указание соответствует рабочей программе курса теоретической механики.
Рис. 6 , библиогр. Назв. 2
Рецензент:
Бартенев Д.А. доц. канд. техн. наук, кафедра ТОХМ СПбГТИ(ТУ)
Утверждено на заседании методической комиссии физико-математического отделения 03.04. 2009
Рекомендовано к изданию РИСо СПбГТИ(ТУ).
2
Содержание |
|
Введение……………………………………………………………...4 |
|
1. Общие теоретические положения...……………………………… |
.5 |
I.I. Работа силы. Мощность……………………………………… |
..5 |
I.2. Кинетическая энергия материальной точки и механической |
|
|
системы……………………………………………………………...7 |
|
|
I.3. Теоремы об изменении кинетической энергии материальной |
|
|
точки и механической системы…………………………………… |
8 |
2. |
Рекомендуемая последовательность решения задач……………...9 |
|
3. |
Примеры решения задач…………………………………………… |
.10 |
3
ВВЕДЕНИЕ
Исследование дифференциальных уравнений движения для решения задач динамики механических систем часто не дает практического результата, так как число уравнений велико, что приводит к математическим сложностям, а внутренние силы и реакции связей, как правило, заранее неизвестны. Поэтому при решении практических задач, в которых не ставится задача определения движения каждой точки системы в отдельности, отказываются от интегрирования дифференциальных уравнений, а вводят некоторые интегральные характеристики, которые описывают движение механической системы в целом. Эти интегральные характеристики движения механической системы вводятся основными теоремами динамики, которые доказываются из дифференциальных уравнений движения механический системы.
Однако введение таких динамических характеристик, как импульс и кинетический момент, не может описать движения механической системы, происходящего под действием внутренних сил, так как главный вектор и главный момент внутренних равны нулю. Проиллюстрируем это на простом примере. Пусть молекула состоит из двух атомов, соединенных между собой связью, которую можно представить в виде пружинки с определенной жесткостью. Система горизонтальна и , неподвижна. Растянув пружину, приводим систему в движение, так как под действием внутренних сил атомы начинают совершать колебания, причем их скорости в каждый момент времени равны по величине и противоположны по направлению. Так как импульс молекулы и ее кинетический момент относительно произвольного центра равны нулю, то они не могут характеризовать движение рассматриваемой системы. Поэтому в теоретической механике вводят еще одну характеристику механического движения, называемую кинетической энергией.
4

1 ОБЩИЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
I.I Работа силы. Мощность
Элементарной работой силы F на бесконечно малом перемещении точки ее приложения dr называется скалярное произведение силы F на дифференциал радиус-вектора dr :
|
|
|
|
|
R |
|
(I.1) |
|
|
|
δA = Fdr |
|
|||
Разложив векторы F и dr |
по осям декартовой системы координат: |
|
|||||
|
|
F = |
V |
R |
|
|
|
|
|
Xi + Yj + Zk |
|
|
|||
|
|
R |
R |
R |
|
|
|
|
|
dr = dxi |
+ dyj + dzk , |
|
|||
получим выражение для δA в координатной форме |
|
||||||
|
|
δA = Xdx + Ydy + Zdz , |
(I.2) |
||||
где X, Y и Z - проекции силы на оси координат. |
|
|
|||||
Так как dr = dSτ , где dS |
- |
элементарное перемещение точки приложения |
|||||
силы F , а τ - орт касательной оси, то |
|
|
|
||||
|
|
δA = |
V |
|
|
R |
(I.3) |
|
|
FτdS = FdS cos(F ,τ ) . |
|||||
Работы силы F |
на конечном перемещении точки ее приложения равна |
||||||
криволинейному интегралу, взятому вдоль кривой из положения М1 |
в положение |
||||||
М2 от элементарной работы (рисунок I.1): |
|
|
|||||
M 2 |
M 2 |
R R |
M 2 |
|
R R |
M 2 |
(I.4) |
А1-2 = ∫ δA = |
∫ |
Fdr = |
∫ |
FdScjs(F ,τ ) = |
∫ ( Xdx + Ydy + zdz). |
||
M 1 |
M 1 |
|
M 1 |
|
|
M 1 |
|
Рисунок I.I.
Из формулы (1.4) следует, что вычисление криволинейного интеграла возможно в тех случаях, когда сила постоянна, или зависит от координат точки приложения силы. В общем случае, когда сила является функцией других переменных, вычислить ее работу нельзя. Поэтому элементарная работа обозначается δA , а не dA , так как не является полным дифференциалом некоторой функции координат точки пространства.
5
n
δA = ∑δAi , а
i=1
n
A1−2 =∑Ai .
i=1
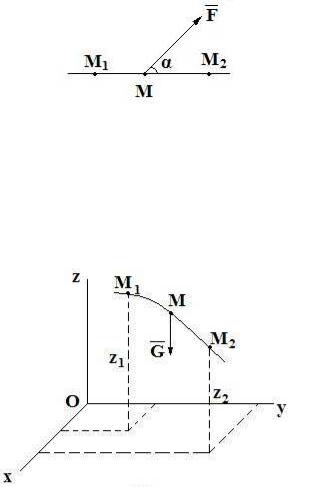
Работа постоянной силы. Работа постоянной силы на прямолинейном перемещении точки равна произведению модуля силы на величину перемещения и на косинус угла между ними (рисунок I.2)
A1−2 = FS cosα |
(I.5) |
Из формулы (I.5) следует, что если угол α |
острый, то работа силы F |
положительна, если угол α тупой, то работа отрицательна, а если α =0, то работа равна нулю.
Рисунок I.2
Работа силы тяжести. Работа силы тяжести материальной точки равна произведению величины силы тяжести на перемещение токи по вертикали (рисунок I.3):
A1−2 = mgh |
(I.6) |
где h = z1 − z2 .
Рисунок |
1.3 |
Работа силы упругости. Работа |
силы упругости равна половине |
произведения коэффициента жесткости на квадрат деформации упругого элемента (рисунок I.4):
A1−2 |
= |
1 |
cλ2 , |
(I.7) |
|
||||
|
2 |
|
|
|
где λ = x1 − x2 .
6
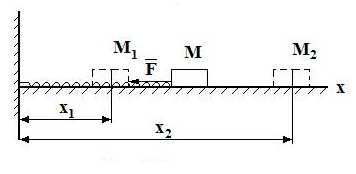
Рисунок 1.4
Работа силы, приложенной к вращающемуся твердому телу.
Элементарная работа силы, приложенной к твердому телу, вращающемуся относительно неподвижной оси вращения на элементарный угол поворота тела:
δA = M z dϕ . |
|
Если M z = const, то |
|
A1−2 = M z (ϕ2 −ϕ1) |
(I.8) |
R R |
(I.9) |
N = δA = FV , |
dt
т.е. мощность равна скалярному произведению вектора силы на вектор скорости
точки ее приложения. Единица измерения мощности – ватт |
( I Вт = I Дж/c). |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
N = M z ω . |
(I.I0) |
|||||||
I.2. Кинетическая энергия материальной точки и механической системы |
||||||||||||||||||
|
|
|
|
|
|
|
|
T = |
1 |
mv2 |
(I.II) |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
1 |
n |
|
||||
|
|
|
|
|
|
T = ∑Ti = |
∑ mi vi 2 . |
|
||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
i=1 |
|
|
|
2 i=1 |
|
|||||
|
|
|
1 |
|
|
|
|
1 |
|
n |
|
|
|
|
||||
T = |
m |
2 |
+ |
|
∑ |
*2 , |
(I.I2) |
|||||||||||
|
|
|
vc |
|
|
|||||||||||||
2 |
|
|
|
2 i=1 |
miV i |
|
||||||||||||
где v - скорость центра масс; |
v * - скорость i-й точки относительно центра масс. |
|||||||||||||||||
c |
|
i |
|
|
|
|
|
|
||||||||||
- при поступательном движении (V * =0) |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
T = |
1 |
|
mV 2 |
; |
|
|
|
|
|
|
|
|
|
(I.I3) |
||||
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
- при вращательном движении (Vc =0) |
|
|||||||||||||||||
T = |
1 |
I zω 2 ; |
|
|
|
|
|
(I.I4) |
||||||||||
|
|
|
|
|
|
|||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
T = |
1 |
mV 2 |
+ |
1 |
I |
ω 2 , |
(I.I5) |
|||||||||||
|
|
|||||||||||||||||
2 |
|
|
|
c |
2 |
|
|
I c |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где СI - мгновенная ось вращения твердого тела с началом в центре масс.
7
I.3. Теорема об изменении кинетической энергии материальной точки и механической системы
mv2 |
|
= δA |
|
|
d |
|
|
(I.I6) |
|
|
||||
|
|
|
|
|
2 |
|
|
|
|
Разделим обе части уравнения на dt и получим иной вид записи теоремы в дифференциальной форме:
d mv2 |
|
= N , |
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
dt 2 |
|
|
||
которая читается так: производная по времени кинетической энергии материальной точки равна мощности равнодействующей всех сил, приложенных к данной точке.
|
mv2 |
2 |
− |
mv12 |
= A |
. |
(I.I7) |
|
|
|
|
||||
2 |
|
2 |
1−2 |
|
|
||
dT = δAE + δAI , |
|
(I.I8) |
|||||
которая читается так: дифференциал кинетической энергии системы равен элементарной работе всех сил, действующих на эту систему. Необходимо
отметить, |
что в указанной теореме речь идет о элементарной работе всех сил, |
||||||
внешних и внутренних. Лишь для твердого тела |
|
||||||
|
|
n |
R |
R |
|
|
|
|
|
|
|
|
|
||
|
|
δA = ∑ Fi E dri . |
|
|
|||
|
|
i =1 |
|
|
|
|
|
|
|
T − T = AE |
+ AI |
, |
(I.I9) |
||
|
|
2 1 |
|
1−2 |
1−2 |
|
|
где AE |
и AI |
- работа внешних и внутренних сил, |
приложенных к точкам |
||||
1−2 |
1−2 |
|
|
|
|
|
|
системы, на перемещениях, произошедших за время изменения кинетической энергии от значения Т1 до значения Т2 .
Заметим, что работа внутренних сил в общем случае не равна нулю и лишь
для абсолютно твердого тела A1I−2 =0, поэтому
(I.20)
C помощью интегральной формы теоремы следует решать те задачи, в которых число данных или искомых величин входят масса m, начальная V1 и конечная V2 скорости, силы (постоянные или зависящие от положения), действующие на точку или систему и перемещение S.
8
2 РЕКОМЕНДУЕМАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РЕШЕНИЯ ЗАДАЧ
1.Выберем величину, определяющую положение точки и указать начало отсчета данной координаты.
2.Изобразить точку в промежуточном положении (t>0).
3.изобразить на рисунке все силы, действующие на материальную точку (активные и реакция связей).
4.Вычислить сумму элементарных работ всех сил на бесконечно малом перемещении точки по формулам (I.I)-(I.3).
5.Вычислить сумму работ всех сил на конечном перемещении точки приложения по формуле (I.4). При действии на точку постоянных сил – силы тяжести и силы упругости, минуя два последних пункта, вычислить работу этих сил на конечном перемещении точки по формулам (I.5)-(I.7).
6.Вычислить кинетическую энергию точки в текущем положении, выразив ее как функцию скорости. Если используется теорема в интегральной форме, то определить кинетическую энергию точки в ее начальном и конечном положениях.
7.Подставить полученные значения в уравнения (I.I6) или (I.I7) и решить их относительно неизвестной величины.
8.Выбрать величину, определяющую положение системы и указать начало ее отсчета.
9.Изобразить на рисунке все кинематические характеристики тел, входящих в эту систему.
10.Определить кинетическую энергию механической системы в начальном и конечных положениях как сумму кинетических энергий тел, входящих в эту систему, по формулам (I.I3)-(I.I5), в зависимости от вида их движения.
11.Изобразить на рисунке все внешние силы.
12.Вычислить сумму полных работ всех внешних сил на конечном перемещении механической системы, пользуясь формулами (I.5)- (I.7).
13.Подставить результаты вычислений в пунктов 3 и 5 в теорему об изменении кинетической энергии в виде (I.20) и из решения полученного уравнения определить неизвестную величину.
9
3 |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ |
Частица массы m |
ПРИМЕР 3.I |
движется горизонтально в вязкой жидкости. Сила |
|
сопротивления движению |
пропорциональна квадрату скорости частицы, т.е |
R = kV 2 . Начальная скорость частицы равна V0 . Определить перемещение точки к моменту времени, когда скорость частицы станет Vk .
РЕШЕНИЕ
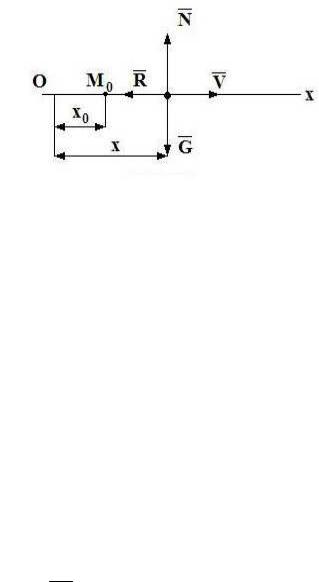
В качестве величины, определяющей положение точки, выбираем координату x и пусть в начальный момент времени x = x0 (рисунок 3.1).
Рисунок 3.1
δA(G ) = Gdx cos 900 = 0 δA(N ) = Ndx cos 900 = 0
δA(R) = Rdx cos1800 = −kV 2dx .
δA = −kV 2 dx
Кинетическая энергия частицы |
T = |
mv2 |
. |
|
|||
|
2 |
|
|
Подставив полученные выражения в уравнение (I.I6), получим
|
|
|
|
2 |
|
|
|
|||
d |
|
|
mv |
|
|
|
= −kV 2dx . |
|||
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
||||
Разделив переменные, получаем |
|
|
|
|
|
|||||
|
m |
|
d (v2 ) |
= −dx . |
||||||
|
|
|
||||||||
|
2k |
v2 |
|
|
||||||
Интегрируем в пределах изменения переменных:
m Vk
2k ∫
V0
d (v |
2 ) |
x |
||
= − ∫ dx . |
||||
v |
2 |
|
||
|
|
x0 |
||
|
|
|
||
Окончательно
10
