Представление графов в эвм

Наиболее распространены следующие 4 метода представления графов в ЭВМ:

• Матрица смежности,

• Матрица инцидентности,

• Списки смежности вершин,

• Списки смежности дуг.

Вы уже имеете представление о представлении графа матрицами смежности и инцидентности (Тема 11, пункт 1). Поясним суть списков смежности вершин.

Списки смежности вершин – представление графа с помощью списочной структуры, отражающей смежность вершин и состоящей из массива указателей на списки смежных вершин, где элемент списка представлен структурой.

Представление графа с помощью массива структур представляется в виде записей: .

Тема 12. Компоненты связности и объединение графов. Оценка числа ребер через число вершин и число компонентов связности. Вершинная и реберная связность. Мосты и блоки.

Объединение графов и компоненты связности. Оценка числа рёбер через число вершин и число компонентов связности. Вершинная и рёберная связность: мосты и блоки, меры связности.

Напомним, что если граф Gсостоит из одной компоненты связности, (то естьk(G) = 1), то он называетсясвязным.

В связном графе любые две вершины соединены (простой) цепью.

Теорема:Граф связен тогда и только тогда, когда его нельзя представить в виде объединения двух графов.

Рассмотрим граф:

V k1 k2

Замечание: Несвязный граф можно всегда представить как объединение связных компонент. Эти компоненты можно рассматривать независимо.

Вершина графа называется точкой сочленения,если ее удаление увеличивает число компонент связности.

В любом нетривиальном графе есть, по крайней мере, две вершины, которые не являются точками сочленения.

Теорема: Пусть р – число вершин,q– число ребер,k– число компонент связности графа. Тогда (p-k) ≤q≤ (p-k)(p-k+1) / 2.

Следствие:Еслиq> (p-1)(p-2) / 2 , то граф связен.

Мостомназывается ребро, удаление которого увеличивает число компонент связ­ности.

Рассмотрим рисунок:

w c d

a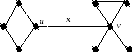

b e f

u,v– точки сочленения, х – ребро-мост,awb,buw,awub,cdv,evf– блоки.

Блокомназывается связный граф, не имеющий точек сочленения.

Если в графе есть мост, то есть и точка сочленения. Концы всякого моста кроме висячих вершин являются точкой сочленения, но не всякая точка сочленения является концом моста.

Вершинной связностьюграфаG(обозначаетсяx(G)) называется наименьшее чи­сло вершин, удаление которых приводит к несвязному или тривиальному графу.

Пример:

æ(G) = 0, еслиGнесвязен;

æ(G) =1, еслиGимеет точку сочленения;

Граф Gназываетсяk-связным,если æ(G) =k.

Реберной связностьюграфаG(обозначаетсяA(G)) называется наименьшее число ребер, удаление которых приводит к несвязному или тривиальному графу.

Пример:

λ(G) = 0, еслиGнесвязен;

λ(G) = 1, если G имеет мост;

λ(К_р) = р-1, значит, граф К_р – полный.

Тема 13. Потоки в сетях. Определение потока. Разрезы. Пример сети с потоками. Теорема Форда и Фалкерсона. Алгоритм нахождения максимального потока.

Потоки в сетях. Примеры практических задач, определение потока, разрезы.

Рассмотрим некоторые примеры практических задач.

Пример:

1) Пусть имеется сеть трубопроводов, соединяющих пункт А (скажем, нефтепромысел) с пунктом В (скажем, нефтеперерабатывающим заводом). Трубопроводы могут соединяться и разветвляться в промежуточных пунктах. Количество нефти, которое может быть перекачено по каждому отрезку трубопровода в единицу времени, также не безгранично и определяется такими факторами, как диаметр трубы, мощность нагнетающего насоса и т. д. (обычно это называют «пропускной способностью» или «максимальным расходом» трубопровода). Сколько нефти можно прокачать через такую сеть в единицу времени?

2) Пусть имеется система машин для производства готовых изделий из сырья, и последовательность технологических операций может быть различной (то есть операции могут выполняться на разном оборудовании или в разной последовательности), но все допустимые варианты заранее строго определены. Максимальная производительность каждой единицы оборудования, естественно, также заранее известна и постоянна. Какова максимально возможная производительность всей системы в целом и как нужно организовать производство для достижения максимальной производительности?

Определения:

Пусть G(V,Е) – сеть, сетью называется граф, имеющий вершины.Sиt– соответственно источник и сток сети. Дуги сети нагружены неотрицательными вещественными числами ЕR+ . Еслиuиv– вершины, то числос(u,v) – называется пропускной способностью дуги (u,v).

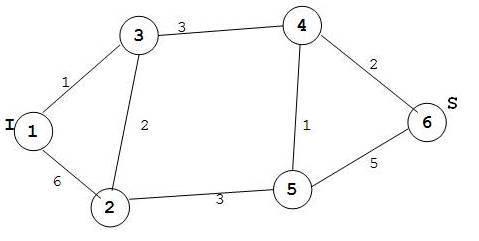
При решении будем полагать, что C(2,1)=C(1,2).

Максимальное количество Xijвещества, которое может пропустить в единицу времени ребро между вершиной (i,j) называют его пропускной способностью.

В общем случае Xij≠Xji. Пропускные способности рёбер сети можно задать квадратной матрицейn-го порядка, гдеn– число вершин сети. В теории потоков предполагается, чтоXii=0. И поэтому главная диагональ матрицы состоит из нулей.

||Cij|| =

1 2 3 4 5 6 0 6 1 0 0 0 6 0 2 0 3 0 1 2 0 3 0 0 0 0 3 0 1 2 0 3 0 1 0 5 0 0 0 2 5 0

Сформируем начальный поток 0, состоящий из суммы потоков по

следующим путям, и найдем пропускные способности путей:

1 = (1, 3, 4, 6), (1 ) = 1;

2 = (1, 2, 3, 4, 6), (2 ) = 2;

3 = (1, 2, 5, 6), (3 ) = 3.

Т.e. пропускная способность потока0 равна:

0 = (1 )+(2 )+(3 ) = 6

Величина потока каждого ребра выглядят так :

(e13) = 1;

(e12) = 4;

(e23) = 1;

(e34) = 2;

(e46) = 2;

(e25) = 3;

(e56) = 3.

Составим теперь матрицу построенного потока ( M2 ) c эле- ментами (eij):

1 2 3 4 5 6

1. 0 4 1 0 0 0

2. -4 0 1 0 3 0

3. -1 -1 0 2 0 0

4. 0 0 -2 0 0 2

5. 0 -3 0 0 0 3

6. 0 0 0 -2 -3 0

Далее строим матрицу М3 = М1 - М2 = { C(eij) - (eij) }:

1 2 3 4 5 6

1. 0 2 0 0 0 0

2. 10 0 1 0 0 0

3. 2 3 0 1 0 0

4. 0 0 5 0 1 0

5. 0 6 0 1 0 2

6. 0 0 0 4 8 0

В соответствии с данным алгоритмом составляем максимальный поток:

1)Построим начальный поток.

2)Составляем по ненасыщенному пути А={1,2,3,4,5,6},где 1Iи

6S,в сответствии с п.2 алгоритма построения по теореме Форда-Фалкерсона,сток попал в количество ребер по ненасыщенному пути.

3)Выделим путь из истока в сток состоящий из ненасыщенных ребер ₄=(1,2,3,4,5,6).

Потом высчитываем С_ij-X_ij:C₁₂-X₁₂=6-4=2,C₂₃-X₂₃=2-1=1,

C₃₄-X₃₄=3-2=1,∆₄₅=1,∆₅₆=2.

Min(C_ij-X_ij)=1,увеличиваем на единицу построенный поток и возвращаемся к п.2(4)=1.

П.2 строим множество по ненасыщенным ребрам А={1,2}

Построим разрез minпропускной способности. Этот разрез будет иметь вид (A\B)=1+2+3=6.

Построим разрез транспортной сети. Он будет пересекать дуги, начало которых принадлежит множеству А,а конец мно-жеству В.

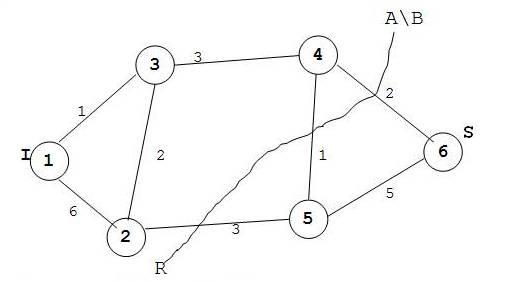
Считаем пропускную способность разреза:

R(A\B)=1+2+3=6.

Таким образом, согласно теореме Форда- Фалкерсона построен

Максимальный поток, равный минимальной пропускной способности pазреза сети.