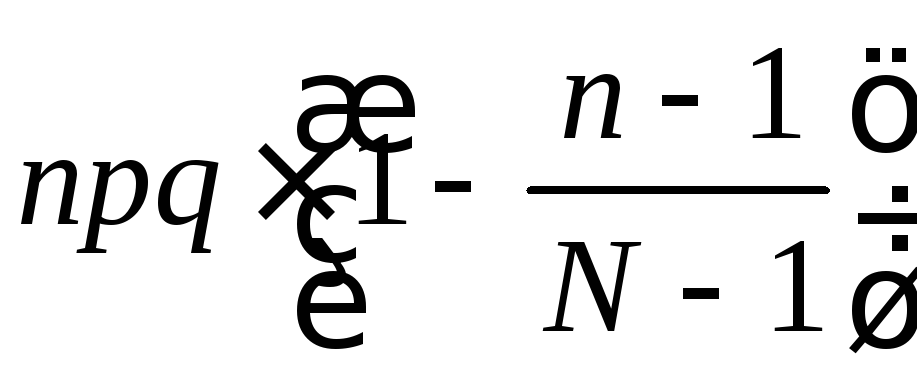- •Федеральное агентство по образованию
- •Isbn Севмашвтуз, 2007
- •Введение
- •Теория вероятностей
- •1. Предмет теории вероятностей. Статистическая устойчивость
- •1.1. Пространство элементарных исходов. Алгебра событий
- •1.2. Классическое определение вероятности
- •1.3. Формулы комбинаторики
- •1.4. Урновые схемы
- •Урновая схема: выбор без возвращения, с учетом порядка
- •Урновая схема: выбор без возвращения и без учета порядка
- •Урновая схема: выбор с возвращением и с учетом порядка
- •Урновая схема: выбор с возвращением и без учета порядка
- •Заметим, что число выборок, различающихся еще и порядком, в k! раз больше, чем число выборок, различающихся только составом.
- •2. Геометрическая вероятность
- •3. Теоремы сложения и умножения вероятностей
- •3.1. Теорема сложения
- •3.2. Условная вероятность
- •3.3. Теорема умножения
- •3.4. Независимые события
- •3.5. Вероятность появления хотя бы одного из событий, независимых в совокупности
- •4. Формула полной вероятности. Формула Байеса
- •4.1. Формула полной вероятности
- •4.2. Формула Байеса
- •5. Схема Бернулли
- •5.1. Формула Бернулли
- •5.2. Теорема Пуассона для схемы Бернулли
- •5.3. Локальная теорема Лапласа
- •5.4. Интегральная теорема Лапласа
- •6. Случайные величины
- •6.1. Законы распределения дискретных случайных величин
- •6.1.1. Распределение Бернулли
- •6.1.2. Биномиальное распределение
- •6.1.3. Геометрическое распределение
- •6.1.4. Распределение Пуассона
- •6.4.5. Гипергеометрическое распределение
- •6.2. Функция распределения св
- •6.3. Непрерывные случайные величины
- •6.4. Числовые характеристики случайных величин
- •6.4.1. Математическое ожидание
- •6.4.2. Мода и медиана св
- •7. Моменты случайных величин
- •7.1. Начальные моменты св
- •7.2. Центральные моменты св. Дисперсия
- •7.2.1. Дисперсия
- •Свойства дисперсии.
- •7.3. Асимметрия и эксцесс
- •Математические ожидания и дисперсии стандартных распределений дсв
- •8. Законы распределения непрерывных случайных величин
- •8.1. Равномерное распределение
- •8.2. Показательное распределение
- •8.3. Нормальное распределение
- •8.3.1. Свойства нормального распределения
- •8.3.2. Стандартное нормальное распределение
- •8.3.3. Правило трех сигм
- •Математические ожидания и дисперсии стандартных распределений нсв
- •Указания к выполнению контрольной работы №1
- •Варианты заданий для контрольной работы №1 вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Список рекомендуемой литературы
- •164500, Г. Северодвинск, ул. Воронина, д.6
7. Моменты случайных величин
Наряду с математическим ожиданием вводятся ещё так называемые начальные и центральные моменты. Их определения одинаковы для дискретной и непрерывной случайной величины.
7.1. Начальные моменты св
Начальным
моментом k-го
порядка
![]() случайной
величины
случайной
величины
![]() называется математическое ожидание отk-той
степени случайной величины:
называется математическое ожидание отk-той
степени случайной величины:
![]() .
.
Для
дискретной СВ:
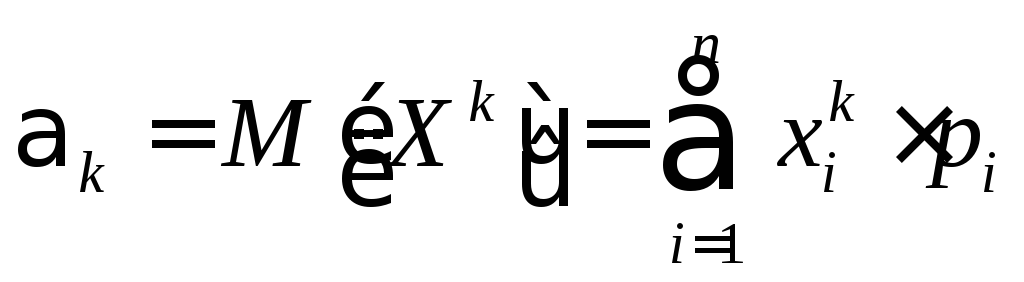 .
.
Для
непрерывной СВ:
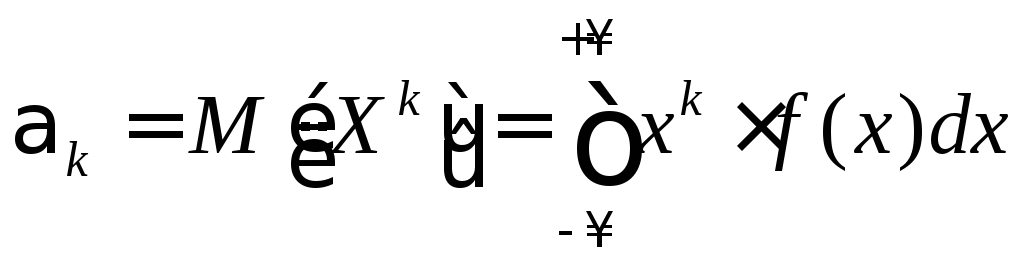 .
.
Основная характеристика положения – математическое ожидание есть первый начальный момент случайной величины.
7.2. Центральные моменты св. Дисперсия
Пусть
![]() – СВ с математическим ожиданием
– СВ с математическим ожиданием![]() .
Рассмотрим отклонение СВ
.
Рассмотрим отклонение СВ![]() от ее математического ожидания:
от ее математического ожидания:![]() .
.
Отклонение
СВ
![]() от ее математического ожидания называетсяцентрированной
случайной величиной
от ее математического ожидания называетсяцентрированной
случайной величиной
![]() .
.
Математическое
ожидание центрированной СВ равно 0:
![]() .
.
Центральным
моментом k-го
порядка
![]() случайной
величины
случайной
величины
![]() называется математическое ожидание отk-той
степени соответствующей центрированной
случайной величины:
называется математическое ожидание отk-той
степени соответствующей центрированной
случайной величины:
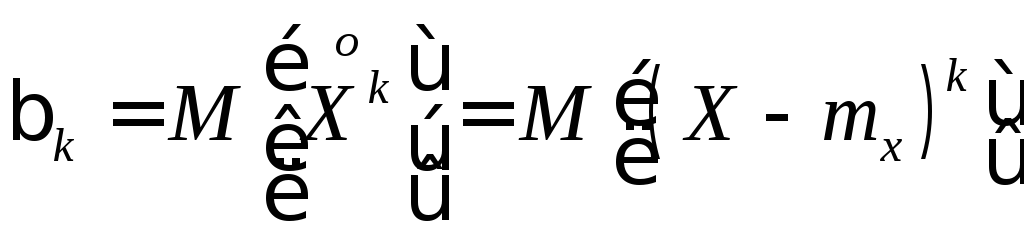 .
.
Для
дискретной СВ:
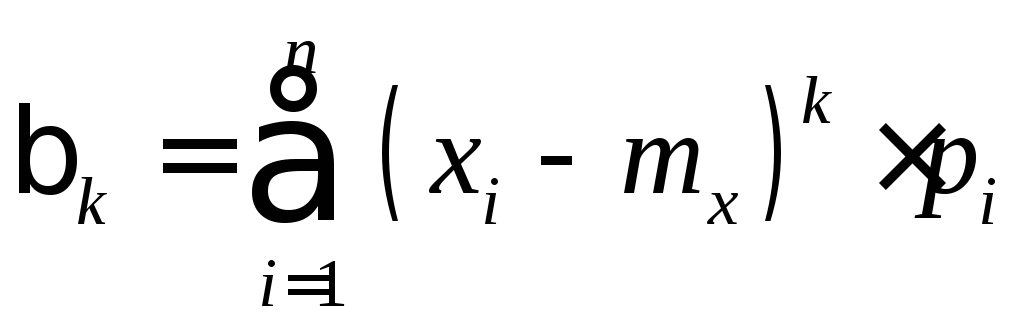 .
.
Для
непрерывной СВ:
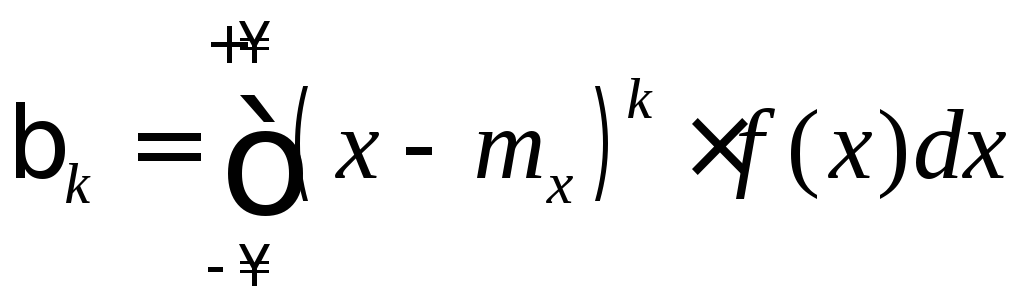 .
.
Центральный момент
1-го порядка
![]() есть математическое ожидание и равен
0.
есть математическое ожидание и равен
0.
7.2.1. Дисперсия
Центральный момент
2-го порядка
![]() называетсядисперсией
случайной
величины и обозначается
называетсядисперсией
случайной
величины и обозначается
![]() .
.
Или: дисперсией называется математическое ожидание от квадрата центрированной случайной величины.
Формулы для вычисления дисперсии:
дискретной СВ
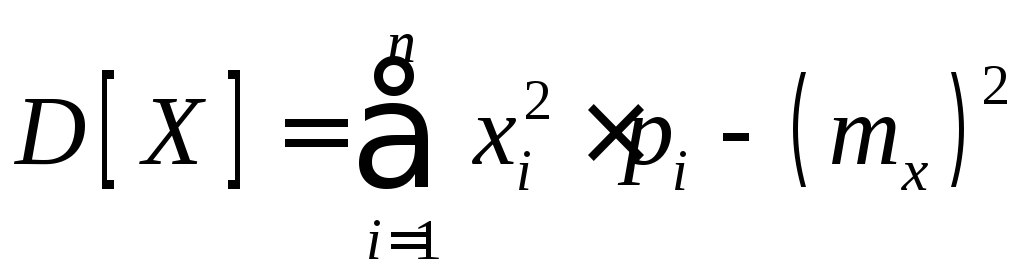 ;
;
непрерывной СВ
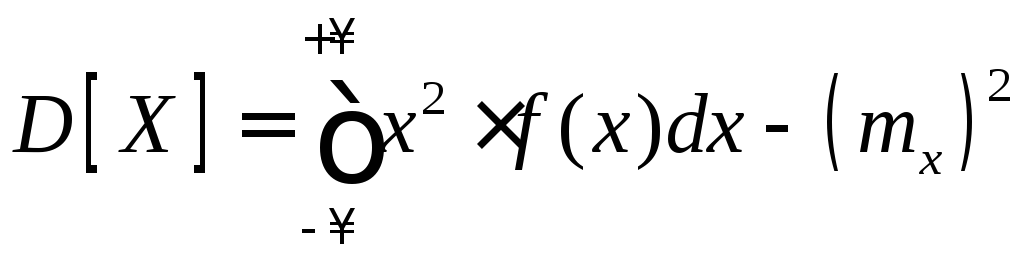 .
.
Дисперсия
![]() есть «среднее
значение квадрата отклонения случайной
величины
есть «среднее
значение квадрата отклонения случайной
величины
![]() от своего среднего». Говорят, чтодисперсия
характеризует степень разброса значений
случайной величины вокруг ее математического
ожидания.
от своего среднего». Говорят, чтодисперсия
характеризует степень разброса значений
случайной величины вокруг ее математического
ожидания.
Если
дисперсия СВ
![]() конечна, то число
конечна, то число![]() называютсреднеквадратическим
отклонением
случайной величины
называютсреднеквадратическим
отклонением
случайной величины
![]() .
.
Свойства дисперсии.
Все свойства дисперсии следуют из соответствующих свойств математического ожидания.
1.
![]() – дисперсия постоянной величины равна
0.
– дисперсия постоянной величины равна
0.
2.
![]()
3.
![]()
Пример. Найти дисперсию случайной величины
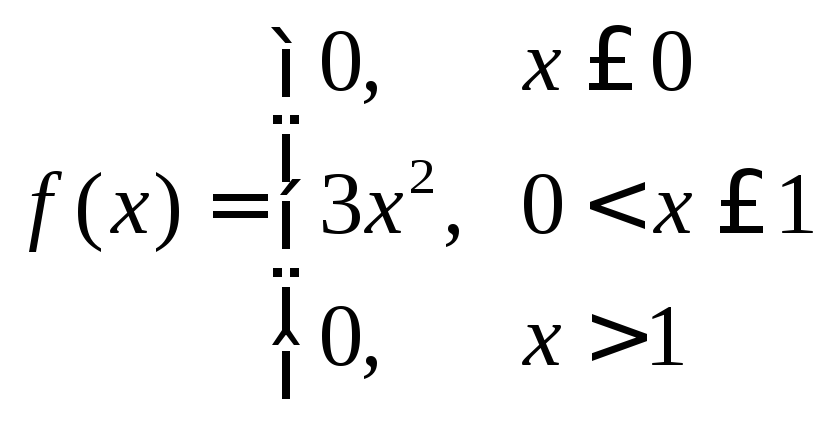 .
.
Решение. Найдем сначала математическое ожидание случайной величины:
![]()
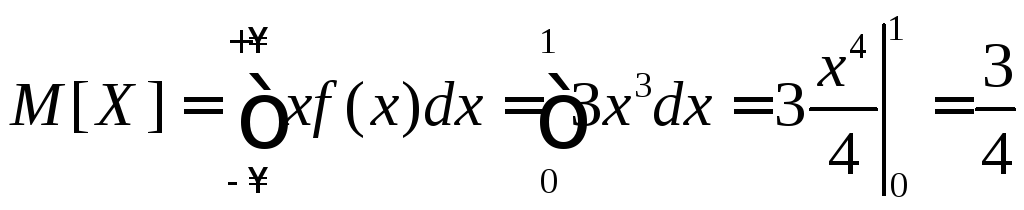 .
.
Дисперсия случайной величины:

7.3. Асимметрия и эксцесс
Рассмотрим
центральный момент 3-го порядка
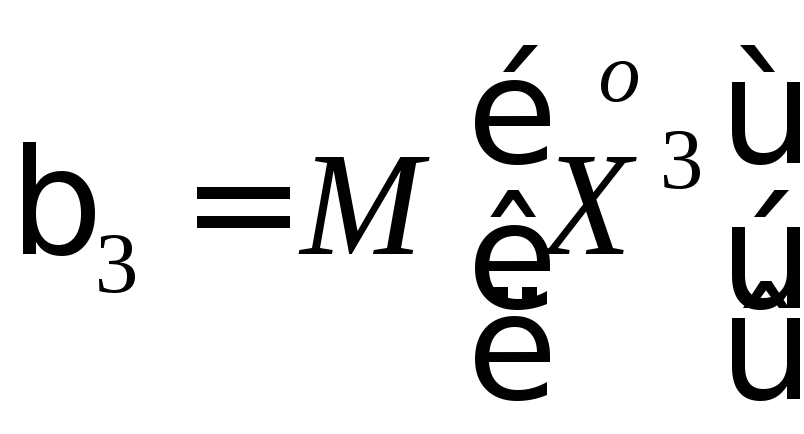 .
.
Величина
![]() называетсякоэффициентом
асимметрии
и характеризует асимметрию (или
«скошенность») распределения. Если
распределение симметрично относительно
математического ожидания, то
называетсякоэффициентом
асимметрии
и характеризует асимметрию (или
«скошенность») распределения. Если
распределение симметрично относительно
математического ожидания, то
![]() (кроме того, все центральные моменты
нечетного порядка в этом случае равны
0).
(кроме того, все центральные моменты
нечетного порядка в этом случае равны
0).
Эксцессом СВ называется величина
![]() ,
,
где
 –
центральный момент 4-го порядка,
–
центральный момент 4-го порядка,![]() – среднеквадратическое отклонение
случайной величины
– среднеквадратическое отклонение
случайной величины![]() .
.
Число 3 вычитается
потому, что для наиболее распространенного
нормального распределения величина
![]() ,
поэтому для нормального распределения
эксцесс равен 0; для кривых, более
островершинных, чем кривая нормального
распределения,
,
поэтому для нормального распределения
эксцесс равен 0; для кривых, более
островершинных, чем кривая нормального
распределения,![]() ;
для кривых, менее островершинных, чем
кривая нормального распределения,
;
для кривых, менее островершинных, чем
кривая нормального распределения,![]() .
.
Математические ожидания и дисперсии стандартных распределений дсв
|
Закон распределения |
Математическое
ожидание
|
Дисперсия
|
|
Биномиальный |
|
|
|
Закон Пуассона |
|
|
|
Геометрический |
|
|
|
Гипергеометрический |
|
|
Пример. Вероятность попадания в цель при одном выстреле равна 0,01. Какова вероятность того, что число попаданий при 200 выстрелах составит не менее 5 и не более 10? Найти математическое ожидание и дисперсию случайной величины Х – числа попаданий в цель.
Решение. Вероятность
![]() очень мала, а число выстрелов (опытов)
достаточно велико. Поэтому искомую
вероятность будем находить, используя
формулу Пуассона. Случайная величинаХ
– число попаданий в цель. Требуется
найти
очень мала, а число выстрелов (опытов)
достаточно велико. Поэтому искомую
вероятность будем находить, используя
формулу Пуассона. Случайная величинаХ
– число попаданий в цель. Требуется
найти
![]() .
Имеем:
.
Имеем:![]() ,
,
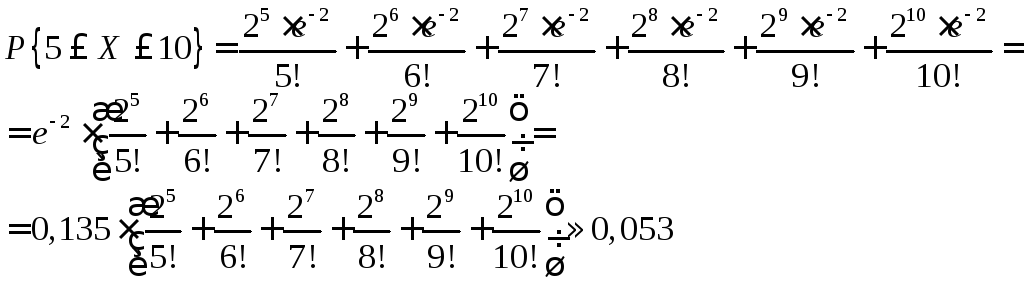
Искомая вероятность
приближенно равна 0,053, а числовые
характеристики данной случайной величины
![]() .
.
Пример.
Вероятность попадания в цель при
отдельном выстреле для данного стрелка
равна 0,1. Найти математическое ожидание
и дисперсию случайной величины
![]() – числа выстрелов по цели до первого
попадания.
– числа выстрелов по цели до первого
попадания.
Решение.
Случайная
величина
![]() имеет геометрическое распределение с
параметром
имеет геометрическое распределение с
параметром![]() .
Тогда
.
Тогда![]() .
.
![]() ,
,
![]() .
.